проект. ГАПОУ НСО. Теорема о проблеме четырёх цветов
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
ГАПОУ НСО «Новосибирский педагогический колледж № 1 имени А.С. Макаренко» Теорема о проблеме четырёх цветов Индивидуальный проект Выполнила: Студентка 11№ группы Б Болгова Ангелина Александровна Консультант: Тимченко Галина Владимировна, преподаватель математики Новосибирск, 2022 Паспорт проекта
СодержаниеВведение 2 Понятие проблемы четырех красок. 3 Что такое «карта»? 3 Теоремы о числе необходимых красок. 6 Практическая часть проекта 7 Применение проблемы в играх и задачах 7 Заключение 12 Список использованной литературы 12 ВведениеПри выборе темы для моей научной работы эта проблема поставила меня в тупик. Какие краски могут быть в математике? Заинтересованная таким необычным названием я решила написать именно про нее. Когда я начинала свою исследовательскую работу, у меня даже не было адекватных предположений - что же это может быть. Как оказалось позже - мое чутье меня не подвело. Я полностью погрузилась в мир… Но, обо всем по порядку. В человеческой деятельности постоянно возникают практические проблемы, которые возможно решить только с помощью математики. Из всех великих математических гипотез следует отметить и знаменитую проблему четырех красок. Итак, цель данного реферата – познакомить вас с проблемой четырех красок и исследовать ее применение при решении задач теории графов. Задачи: 1.Узнать историю возникновения данного парадокса. 2. Понять принцип теоремы. 3.Узнать, какие виды графов применяются к проблеме четырёх красок. 4. Применить теорему при решении задач. 5.Создать свой рисунок, соблюдая правило «Теоремы о четырёх красках». Этой теме посвящено много литературы. Об этом писал Мартин Гардер, рассказывая о разнообразных применениях проблемы четырех красок. Актуальность этой темы заключается в том, что зная суть этой проблемы, становится намного проще решать математические задачи, а также интересно проводить время с друзьями. Понятие проблемы четырех красок.Изначально эту проблему подняли географы. Раскрашивая карты, они стараются обойтись минимальным количеством цветов, при этом сделать это так, чтобы две страны граничащие друг с другом были закрашены разными цветами. Проблема 4 красок зародилась в 1852 году, когда Френсис Гутри, раскрашивая карту графств Англии, заметил, что 4 красок ему хватает, а вот тремя - не обойтись. Возник естественный вопрос - для раскраски любой ли карты хватит четырех красок? Проблема быстро дошла до математической общественности и была сформулирована в 1878 году английским математиком А.Кэли следующим образом: «Всякую ли расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок, границы были раскрашены в разные цвета?» В 1913 году эта теорема было доказана для 25 стран, через год для 38. Но проблема становилась совершенно непреступной с лавинообразным увеличением числа стран. Более ста лет математикам не удавалось получить доказательства. Лишь в 1976 году К. Аппель и В. Хакен - профессора Иллинойского университета, добились успеха благодаря новаторскому шагу, - применив компьютер для доказательства теоремы. Что такое «карта»?Конечно, все это звучит умно и красиво, но, начиная разбирать эту проблему, сначала стоит пояснить, что же такое «карта». Хотя понятие карты является довольно естественным и опирается на представления о географических картах, тем не менее, вопрос о том, что такое карта не такой простой, как кажется на первый взгляд. Конечно, для решения задачи о раскраске конкретной карты определение карты неважно. Однако если мы хотим устанавливать справедливость общих свойств для некоторых классов карт, или даже для всех карт, то определение карты становится важным. От него зависит справедливость общих свойств. Итак, посмотрим, какие бывают карты. Многоугольной картой на плоскости будем называть разбиение многоугольника на более мелкие многоугольники получающиеся добавлением новых вершин и сторон внутри данного многоугольника, причем любые два новых многоугольника или не имеют общих точек или имеют общие вершины или имеют общие стороны. Многоугольники называются странами, а их стороны - границами. Пример такой карты приведен на рисунке ниже. 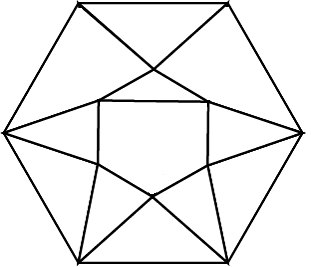 Иногда к многоугольной карте в качестве дополнительных стран присоединяют одну или несколько внешних бесконечных областей плоскости ограниченных сторонами исходного многоугольника и лучами. Пример такой карты приведен на рисунке. Новые страны помечены цифрами 1,2,3,4. 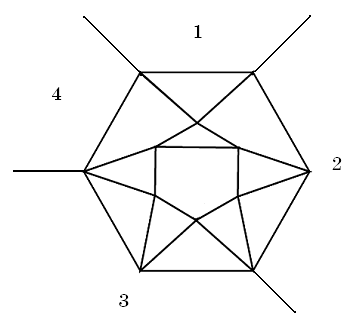 Рассматриваются также карты составленные из многоугольников заполняющих всю плоскость . Как и раньше требуется чтобы любые два многоугольника или не имели общих точек или имели общую вершину или сторону. Пример таких карт дают паркеты, некоторые из которых представлены на рисунке. 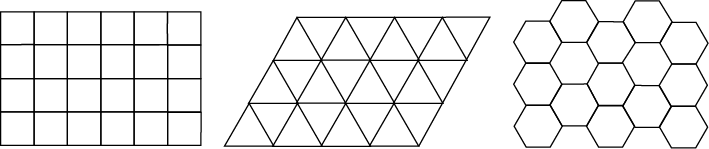 Заметим, что для задачи раскрашивая карты неважно, какими являются границы стран прямыми или нет. Карту можно немного растягивать сжимать искривлять стороны и при этом число красок необходимых для ее правильного раскрашивания не изменится. Мы будем рассматривать и такие карты. На рисунке показана многоугольная карта и карта полученная из нее искривлением сторон. 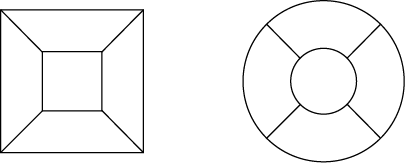 Помимо плоскости карты рассматривают и на других поверхностях, например, на сфере. Поверхность многогранника можно рассматривать как карту, странами которой являются грани многогранника, а границами его ребра. На рисунке показаны карты образованные поверхностями правильных многогранников: тетраэдра, куба, октаэдра, икосаэдра и додекаэдра. 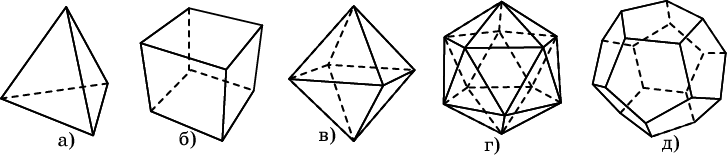 Теоремы о числе необходимых красок.В ходе раскрашивания различного вида карт были сделаны следующие выводы. Если в каждой вершине карты сходится четное число ребер, то нам понадобиться 2 краски.  Если в каждой вершине карты сходится нечетное число ребер, а каждая грань имеет нечетное число сторон, то потребуется А) 3 краски  Б) 4 краски. 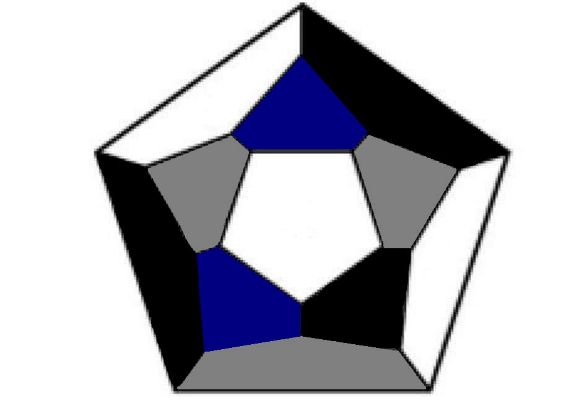 Если карта образованна двумя концентрированными окружностями с некоторым количество перегородок, то: А) Если при этом количество перегородок является четным числом , то потребуется 3 краски. 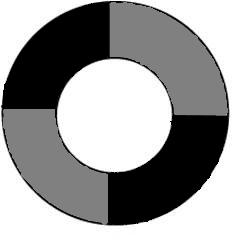 Б) Если количество перегородок является нечетным числом, то потребуется 4 краски. 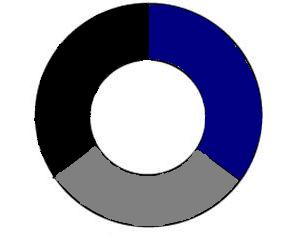 Практическая часть проектаПрименение проблемы в играх и задачахИгра «Четыре краски» Познакомившись с проблемой красок, математик Стивен Барр придумал логическую игру для двух игроков названную «Четыре краски». По словам Мартина Гарднера — «Я не знаю лучшего способа понять трудности, которые встречаются на пути решения проблемы четырёх красок, чем просто поиграть в эту любопытную игру» Для этой игры нужны четыре цветных карандаша. Первый игрок начинает игру, рисуя произвольную пустую область. Второй игрок закрашивает её любым из четырёх цветов и в свою очередь рисует свою пустую область. Первый игрок закрашивает область второго игрока и добавляет новую область, и так далее — каждый игрок раскрашивает область соперника и добавляет свою. При этом области, имеющие общую границу, должны быть раскрашены в разные цвета. Проигрывает тот, кто на своём ходу вынужден будет взять пятую краску. Важно заметить, что проигрыш в этой игре вовсе не означает, что теорема о четырех красках неверна. Те же области можно раскрасить верным для теоремы способом – так, как на правом рисунке. Я познакомила с этой игрой своих одноклассников, и мы с удовольствием играем в эту игру в свободное время. Выигрышной стратегии мы пока не нашли, но, я думаю, все еще впереди. На рисунке ниже приведена типичная картинка, которая остается после очередной игры «Четыре краски» 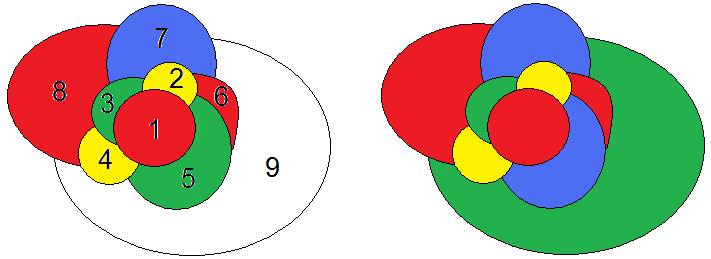 Хочу так же привести несколько задач данной тематики которые обязаны своим рождением так долго не решаемой проблемы 4 красок. Задача 1. Раскрасьте эту карту из 100 стран в четыре цвета так, чтобы соседние страны были окрашены в разные цвета. Решение приведено на рисунке снизу. 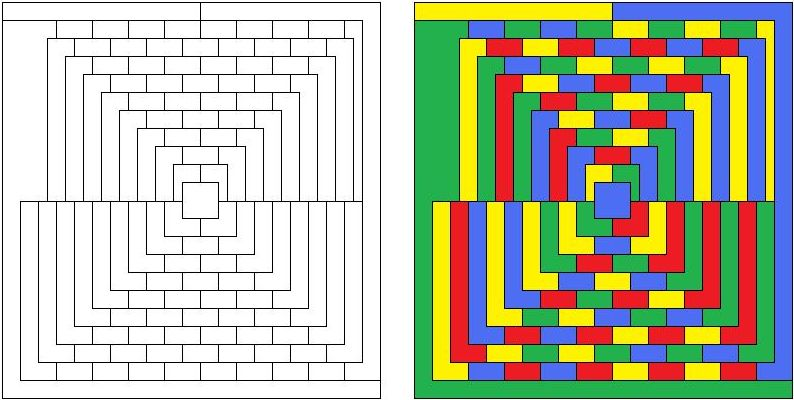 Задача 2. Дано: На плоскости проведено n прямых. Докажите, что такую абстрактную карту можно раскрасить двумя красками так, чтобы любые две области, имеющие общие участок границы, были раскрашены в разные цвета.  Доказательство: Применим метод математической индукции по числу прямых. Очевидно, карту, образованную одной прямой, можно раскрасить в два цвета. Пусть утверждение доказано для n прямых на рисунке слева. Проведем (n+1)-ю прямую на рисунке в центре. В одной полуплоскости этой прямой цвета областей оставим без изменений, а в другой полуплоскости изменим цвет каждой желтой области на голубой, а цвет каждой голубой области на желтый. При этом на рисунке справа получим раскраску, в которой любые две области, имеющие общий участок границы, раскрашены в разные цвета. Утверждение доказано. 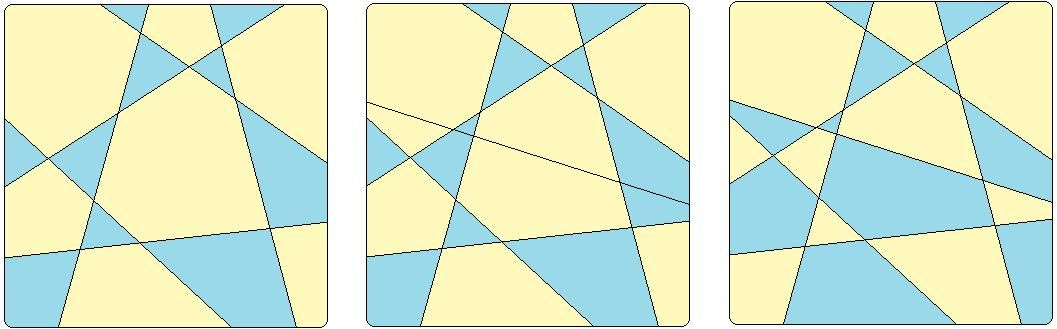 Задача 3. Дано: На плоскости задано n окружностей. В каждой окружности проведено по хорде так, что хорды двух окружностей имеют между собой не более 1 общей точки. Докажите, что получившуюся карту на рисунке всегда можно раскрасить темя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. 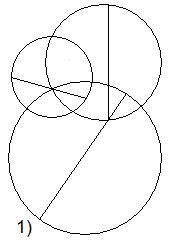 Доказательство: Идею доказательства проведем для трёх окружностей с хордами, хотя все рассуждения можно обобщить на случай, когда на плоскости нарисовано n окружностей с хордами. Состоит она в следующем: Первая, малая окружность и её хорда разбивает плоскость на три части. Во всех областях первой части поставим по 0, во всех областях второй части поставим 1, во всех областях третьей части поставим 2 (рис. 2); Вторая, средняя окружность и её хорда разбивает плоскость на три части. Во всех областях первой части поставим по 0, во всех областях второй части поставим 1, во всех областях третьей части поставим 2 (рис. 3); Третья, большая окружность и её хорда разбивает плоскость на три части. Во всех областях первой части поставим по 0, во всех областях второй части поставим 1, во всех областях третьей части поставим 2 (рис. 4). При этом каждой области будет соответствовать три числа, найдем их сумму (рис. 5), и числа каждой области заменим остатком от деления его на 3 (рис. 6). Области, у которых этот остаток равен 0, закрасим синей краской; Области, у которых этот остаток равен 1, закрасим желтой краской; Области, у которых этот остаток равен 2, закрасим красной краской. Полученная таким образом раскраска (рис. 7) удовлетворяет условия задачи. 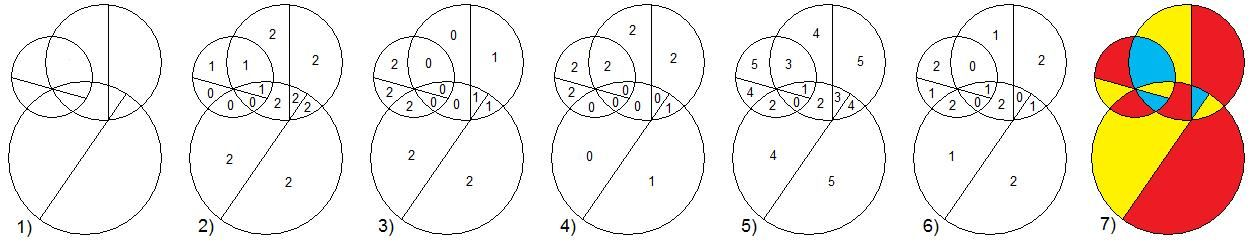 ЗаключениеДа, теорема о четырех красках доказана и принята математическим сообществом, но у части математиков её доказательство вызывает определенное недоверие в той его части, где значительную часть рутинных проверок выполнял компьютер. Сами авторы доказательства сообщают: "Читатель должен разобраться в 50 страницах текста и диаграмм, 85 страницах с почти 2500 дополнительными диаграммами, 400 страницами микрофишей, содержащими еще диаграммы, а также тысячи отдельных проверок утверждений, сделанных в 24 леммах основного текста. Вдобавок читатель узнает, что проверка некоторых фактов потребовала 1200 часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно". Решение проблемы четырёх красок есть первая математическая теорема, при доказательстве которой впервые был использован компьютер, и является примером неклассического доказательства в современной математике. «Так решена ли проблема четырех красок?», – каждый вправе задать себе такой вопрос. Я думаю, правильный ответ на него даст время. Список использованной литературыМ. Гарднер, Математические головоломки и развлечения, М.: Мир, 1999 г. – 447 с. Методы четырехцветной раскраски вершин плоских графов. — М.: КомКнига, 2000. — 48 с. Самохин А. В. Проблема четырех красок: неоконченная история доказательства //СОЖ. — 2000. — № 7. — С. 91—96. Родионов В. В. Методы четырехцветной раскраски вершин плоских графов. — М.: КомКнига, 2000. — 48 с. Рингель Г. Теорема о раскраске карт / Перевод с английского В. Б. Алексеева. — М.: Мир, 1977. — 256 с. — книга с доказательством проблемы для всех поверхностей, кроме плоскости и сферы. |
