Занятие 8. Теорема остроградского гаусса
 Скачать 0.92 Mb.
|
Решение1. Изобразим на рисунке силовые линии поля цилиндра. Линии начинаются на поверхности трубки и идут по радиусам перпендикулярно поверхности (боковой) цилиндра (рис.8.6). 2. Исходя из этих соображений, охватывающая заряд поверхность должна быть цилиндрической, тогда  перпендикулярен боковой поверхности, cos = 1, т.к. = ( ) = 0.Поток через основания трубки равен нулю, т.к. = ( ) = 900, cos = 0.Для точки 1 поверхность, проходящая через точку, тоже цилиндрическая, радиус основания цилиндра равен  . Заряда же внутри металлической трубки быть не может. Поэтому Следовательно, DS1 = 0; D = 0 и E = 0. Точка 2. Охватывающая поверхность – цилиндра радиусом R; охваченный поверхностью заряд q = S2, где - поверхностная плотность заряда.  где h – высота цилиндра. D S2 = q; D S2 = S2; D = ;  Точка 3. Поток  через поверхность, проходящую через точку 3, Заряд, охваченный поверхностью,  Приравниваем  по теореме Остроградского – Гаусса:  Построим графики зависимостей D и E от r (рис. 8.7, 8.8). 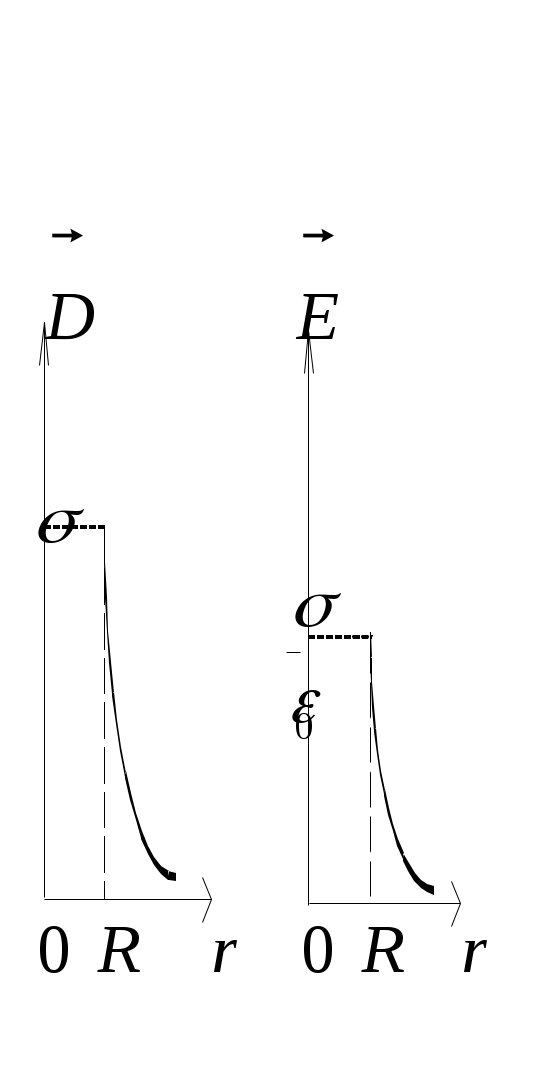 Рис.8.7 Рис.8.8 Напряжённость и индукция электрического поля внутри цилиндра равна нулю, а снаружи, начиная с поверхности, убывает обратно пропорционально расстоянию.Ответ: а) D1 = 0; E1 = 0; б) D2 =10-9  ; E2 = 1,12 .102  ; в) D3 = 6,7 .10-10  E3 = 75,5 .3. На металлической сфере радиусом R = 10 см находится заряд q = 10-9 Кл. Определить напряжённость электрического поля в точках: а) на расстоянии 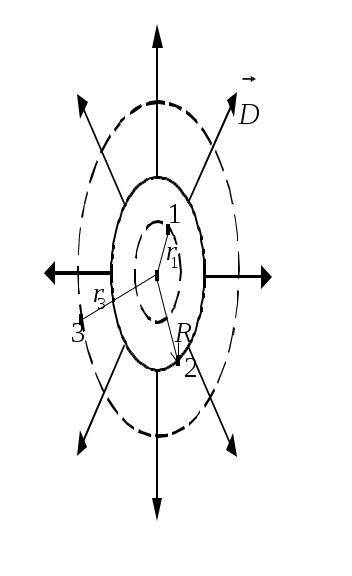= 8 см от центра сферы; б) на поверхности её; в) на расстоянии  = 15 см от центра сферы (рис.8.9). Построить графики зависимостей E и D от r.  Дано: q = 10-8 Кл R = 10 см =10-1 м = 8 см = 8 .10-2 м  = R =10 см = 0,1 м  = 15 см = 0,15 м Е1 - ? Е2 - ? Е3 - ? Рис.8.9 Решение Зарядов внутри сферы нет, линии индукции начинаются на её поверхности. Поле сферически симметричное, как у заряженного шара. Охватывающей поверхностью будет сфера, проходящая через заданную точку, т.к. перпендикулярен к сферической поверхности.а) Сфера, проведённая через точку 1 (r < R) не охватывает никаких зарядов, следовательно, q = 0,  = 0, D1 = 0 , Е1 = 0. б) Сфера, проведённая через точку 2 (r = R), охватывает весь заряд, находящийся не её поверхности:  Поток линий индукции через эту поверхность Фe2 = D2 S2 = D2 4R2. Тогда по теореме Остроградского – Гаусса  в) Сфера, проведённая через точку 3, охватывает тоже весь заряд, находящийся на поверхности металлической сферы: Поток  Тогда  Отсюда следует, что напряжённость, созданная заряженной сферой на её поверхности и вне сферы, такая, которую создал бы точечный заряд, если бы он был расположен в центре сферы. Графики зависимости D и Eот r приведены на рис.8.10 и 8.11. 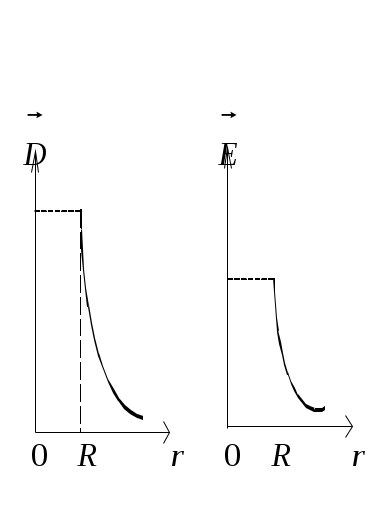 Рис.8.10 Рис.8.11 Ответ: а) D1 = 0; E1 = 0; б) D2 = 8 .10-8 ; E2 = 900 ;в) E3 = 400 .4. К бесконечной плоскости, вдали от её краёв, подвешен на шёлковой нити шарик массой m = 2 г. Шарик заряжен электрическим зарядом того же знака, что и плоскость. Определить заряд шарика, если нить образует с плоскостью угол 300. Поверхностная плотность заряда плоскости = 6,7 .10-5 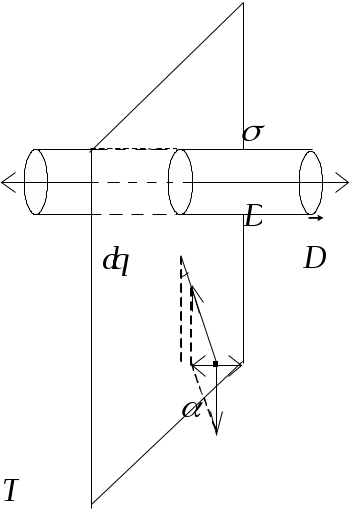(рис.8.12). Д  ано: = 6,7  m = 2 г = 2 .10-3 кг  = 300q - ? Решение Заряженная плоскость создаёт электрическое поле напряжённостью  , в результате чего на шарик действует сила  Кроме того, на шарик действуют силы  и  , где - сила натяжения нити, а  - сила тяжести. Равнодействующая этих сил направлена по одной линии с силой  и уравновешивает её. (1)Для вычисления и  применим теорему Остроградского – Гаусса. Поле бесконечной плоскости вдали от её краёв является однородным (см. рис.8.12).Выделим элементарный заряд  и построим на нём цилиндрическую поверхность, перпендикулярную плоскости.Поток проходит через основание цилиндра и не проходит через боковую поверхность, т.к. перпендикулярен плоскости и направлен вправо и влево от заряда dq: тогда  откуда  а напряжённость поля равна Подставив в выражение (1), получим:  9 .10 9  Вычислим  Кл = 3 .10 -9 Кл.Ответ: q = 3 .10-9 Кл. 5. Электрическое поле создано двумя параллельными бесконечными плоскостями с поверхностными плотностями заряда  = 0,4  и  = 0,1 : а) заряды п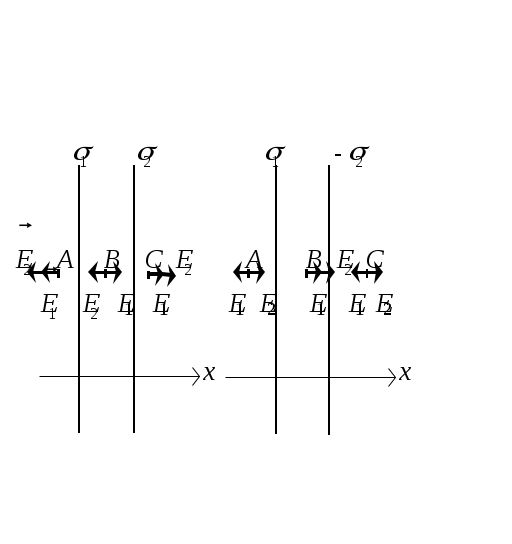оложительны; б) заряды разноименные (рис.8.13). Определить напряжённость электрического поля, созданного этими плоскостями в точках А, В и С.Д  ано = 0,4 .10-6 = 0,1 .10-6  Е1 - ? Е2 - ? Е3 - ?  а) б) Рис.8.13 Решение Каждая из плоскостей создаёт поле, напряжённость которого определяется по теореме Остроградского – Гаусса:  Суммарная напряжённость находится по правилу сложения векторов. Направления  и  указаны на рис. 8.13(а, б). и направлены по одной линии:а) Заряды одноименные     б) заряды разноимённые, тогда ЕА = Е2 – Е1; ЕВ = Е1 + Е2; ЕС = Е1 – Е2.  . .Ответ: а) ЕА = ЕС = 2,83 .104 ; ЕВ = 1,7 .104 ; б) ЕА = ЕС = 1,7 .104 ; ЕВ = 2,83 .104 .Задачи для самостоятельного решения Задача 1. Две плоские пластинки площадью 200 см2, заряженные равными зарядами, притягиваются, находясь в керосине, с силой 2,5 10-2 Н. Расстояние между пластинками столь мало, что напряжённость поля можно рассчитывать по формуле для бесконечных плоскостей. Определить: а) находящиеся на них заряды; б) индукцию электрического поля в керосине.Ответ: а) q = 1,33 .10-7 Кл; б) D = 3,3 .10-6 .Задача 2. Металлический шар радиусом 2 см окружён сферической металлической оболочкой радиусом 4 см, концентрической с шаром. На шаре находится заряд 2 .10-8 Кл, на оболочке – заряд -4 .10-8 Кл. Определить напряжённость поля: а) на расстоянии 3 см от центра шара; б) на расстоянии 5 см от центра. Ответ: а) Е1 = 2 .105 ; б) Е2 = 7,2 . .Задача 3. Плоский слой диэлектрика ( = 2) толщиной 0,5 см равномерно заряжен электричеством с объёмной плотностью заряда = 3 .10-4  . Какова напряжённость поля: а) в середине слоя? б) внутри слоя на расстоянии 0,1 см от поверхности? в) вне слоя? |