Теоретическая механика. Ответы на вопросы экзамена. Теоретическая механика. Теоретическая механика Аксиомы статики
 Скачать 476.84 Kb.
|
|
Теоретическая механика 1. Аксиомы статики. Аксиома инерции: Под действием уравновешенной системы сил материальная точка (тело) находится в состоянии покоя или движется равномерно и прямолинейно. Аксиома равновесия 2-х сил: Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой в противоположные стороны. Аксиома присоединения и исключения уравновешивающих сил: Не нарушая состояние абсолютно твердого тела, к нему можно прикладывать или отбрасывать от него уравновешивающую систему сил. Аксиома параллелограмма сил: Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту же точку и равную их геометрической сумме. Аксиома равенства действия и противодействия: Силы взаимодействия 2-х тел равны по модулю и направлены по одной прямой в противоположные стороны. Аксиома о сохранении равновесия сил, приложенных к деформированному телу: Равновесие деформируемого тела не нарушится, если это тело отвердеет. 2. Определение равнодействующей и уравновешивающей произвольной системы сил. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Силой, уравновешивающей систему сил, называют такую силу, которая будучи присоединенной к данной системе сил, оставляет вместе с ней новую систему сил, эквивалентную нулю. 3. Сходящаяся система сил. Сходящаяся система сил – это система таких сил, линии действия которых полностью сходятся в одной точке. Действие каждой силы на абсолютно твердое тело не меняется при переносе силы вдоль линии ее действия на иную точку тела. 4. Равнодействующая система сходящихся сил. Сходящаяся система сил имеет равнодействующую, приложенную в точке пересечения линий действия сил системы и равную векторной сумме всех сил системы.  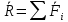 5. Условия равновесия системы сходящихся сил в векторной форме и в проекциях на оси декартовой системы координат. Сходящаяся система сил является уравновешенной тогда и только тогда, когда векторная сумма всех сил системы равна нулю. 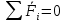 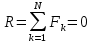 Если R – вектор, замыкающий силовой многоугольник: Геометрическое условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут. 6. Теорема о трех уравновешенных силах. Если под действием трех сил тело находится в равновесии, и линии двух действующих сил пресекаются, то все силы находятся в одной плоскости, и их линии действия пересекаются в одной точке. 7. Определение алгебраической величины момента силы относительно векторного центра. Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы. 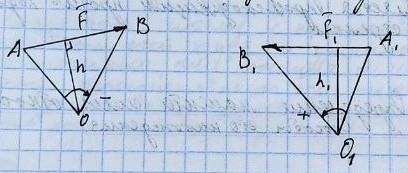 8. Сформулируйте и запищите векторное выражение момента силы относительно некоторого центра. Моменты силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы. 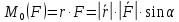 9. Почему для плоской системы сил нет необходимости придавать векторный смысл моменту силы? В случае плоской системы сил силы относительно точки можно принимать за алгебраическую величину. Для пространственной системы сил момент – это вектор, который направлен перпендикулярно к плоскости, в которой лежат сила и точка, в ту сторону, откуда вращение тела сил представляется происходящим против хода часовой стрелки. 10. Определение моменты силы относительно оси. Способы его нахождения. Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярно к данной оси, относительно точки пересечения этой плоскости с осью. Момент силы относительно оси равен проекции на эту ось вектора момента силы относительно произвольной точки, лежащей на этой оси. Если сила Fзадана своими проекциями 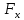 ,  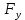,  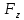и координатами x, y, z точки приложения, то момент силы относительно начала координат может быть представлен в виде определителя 3-го порядка: Для определения знака момента удобно рассматривать систему с положительных направлений оcей x, y, z и принимать момент положительным, если проекция силы на плоскость, перпендикулярную оси, пытается создавать вращательный эффект вокруг этой же оси против хода часовой стрелки. 11. Определение пары сил и момента пары сил. Система двух равных по величине, антинаправленных и не лежащих на одной прямой сил называется парой сил. Пара сил не имеет равнодействующей, то есть заменена эквивалентной силой. Момент пары сил есть вектор, перпендикулярный к плоскости действия пары, направленной в сторону, откуда поворот тела данной парой виден происходящим против хода часовой стрелки. 12. Как направлен вектор момента пары сил? Момент пары сил, то есть вектор M(   ) всегда перпендикулярен плоскости, в которой расположена пара сил, и его направление определяется правилом векторного произведения: 13. Определение главного вектора и главного момента произвольной пространственной системы сил. Сила R, равная геометрической сумме всех сил данной системы, называется главным вектором:  Величина  , равная геометрической сумме моментов всех сил систем относительно центра произведения, называется главным моментом относительно этого центра: 14. Чем отличаются главный вектор от равнодействующей произвольной системы сил? Равнодействующая система сил эквивалентна системе сил, а главный вектор сам по себе не эквивалентен данной системе сил, но эквивалентен ей только в совокупности с главным моментов. 15. Определение центра тяжести. Способы определения координат центра тяжести. Центром тяжести тела называется центр системы параллельных сил, которую приближенно образуют силы тяжести его элементарных частиц. Способы: Аналитический (путем интегрирования) Метод симметрии: Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно там. Экспериментальный (путем подвешивания) 16. Метод отрицательных масс и метод разбивания на части при определении координат центра тяжести. Дополнение (Метод отрицательных площадей и объектов) (отрицательных масс)     Разбиение на части Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести Cи площади Sизвестны.    17. Дайте определение момента пары сил. Как направлен вектор-момент пары? Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение. Вращательный эффект пары сил характеризуется векторной величиной, называемой моментом пары сил. Момент пары сил относительно точки O:  Момент пары сил перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары сил:   18. Напишите аналитические выражения для главного вектора и главного момента. Выразим главный вектор сил через его проекции на координатной оси:  где:  , , – проекции главного вектора на оси x, y, z. где:  ,  ,  – проекции силы  на оси x, y, z.Модуль главного вектора определяется:  Главный момент:  где:  ,  ,  – проекции вектора на оси  19. В чем состоит метод отрицательных масс и метод разбиения на части при определении координат центра тяжести? Метод отрицательных масс: «Частный случай метода разбиения» Используется при определении положения центра масс фигуры, имеющей вырезы. Массу удаленного участка считают отрицательной, а силу тяжести этого участка (-mg) направляют вверх. В дальнейшем используют условие равновесия тела, находящегося под действием системы параллельных сил. Метод разбиения на части: Состоит в том, что рассматриваемое тело мысленно разбивается на части, центры тяжести которых известны либо могут быть легкоопределимы, после чего применяются формулы для определения координат центра системы параллельных сил. 20. Определение скорости и ускорения при векторном способе задания движения. Скорость – вектор, характеризующий быстроту изменения положения точки по величине и направлению.  Ускорение – вектор, характеризующий быстроту изменения скорости точки по величине и направлению.  21. Поступательное движение тела. Определение скоростей и ускорений точки. Поступательным называется такое движение тела, при котором прямая, соединяющая 2 любые точки этого тела, перемещается, оставаясь параллельной своему начальному направлению. При поступательном движении точки тела могут двигаться по любым траекториям. 22. Вращательное движение твердого тела, угловая скорость, угловое ускорение. Вращением твердого тела вокруг неподвижной оси называют такое движение тела, при котором хотя бы 2 его точки остаются неподвижными. Неподвижная прямая проходящая через 2 неподвижные точки тела называется осью вращения тела. Мера изменения угла поворота с течением времени называется угловой скоростью.  Величина, характеризующая изменение угловой скорости с течением времени, называется его угловым ускорением.  23. Плоское движение твердого тела. Плоское движение твердого тела – это такое движение, при котором каждая точка движется в плоскости, которая параллельна некоторой неподвижной плоскости. Такое движение совершает колеса или шатун в кривошипно-шатунном механизме. 24. Мгновенный центр скоростей. Частные случаи его определения. Мгновенным центром скоростей называется точка сечения тела, скорость которой в данный момент времени равна 0. Частные случаи МЦС: Если  : AB γ  , AB γ     25. Сложное движение точки. Общие сведения. В ряде случаев при решении задач по механике оказывается целесообразным рассматривать движения одновременно по отношению к двум системам отсчета, одна из которых является основной или условно-неподвижной. Другая система отсчета (подвижная) движется определенным образом по отношению к первой. Движение, совершаемое при этом точками или телом, называется составным или сложным. Движения, совершаемые связанной точкой по отношению к подвижной системе отсчета, называется относительным движением точки. По отношению к подвижной системе отсчета точка обладает относительной скоростью  и относительным ускорением  .Движения, совершаемые подвижной системой отсчета вместе со связанными с этой системой точками пространства по отношению к неподвижной системе, являются для связанной точки переносным движением. Связанная точка обладает переносной скоростью  и переносным ускорением  .Движения, совершаемые связанной точкой относительно неподвижной системы отсчета, называются абсолютным движением. Абсолютная скорость  равна геометрической сумме относительной и переносной скоростей.  26. Лемма Пуансо Всякая сила, приложенная к твердому телу эквивалентна такой же силе, но приложенной в другой точке тела, не лежащей на линии действия первой силы, и паре сил с моментом, равным моменту первой силы относительно точки приложения второй силы. 27. Теорема Вариньона. Момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов, составляющих систему сил относительно того же центра.  28. Центр параллельных сил. Центром параллельных сил называется точка, при повороте вокруг которой всех сил системы на один и тот же угол, линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол. Свойства центра параллельных сил: Сумма моментов всех сил  относительно точки C равна нулю.  Если все силы повернуть на некоторый угол α, не меняя точек приложенных сил, то центр новой системы параллельных сил будет той же точкой C. 29. Теорема о сложении скоростей. При сложении движений абсолютная скорость точек равна геометрической сумме относительной и переносной скоростей.  30. Теорема о сложении ускорений. Теорема Кориолиса: При сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и поворотного (кориолисова).   31. Аксиомы динами точки. Закон инерции: Изолированная материальная точка находится в состоянии покоя или совершает равномерное и прямолинейное движение.  Свойство тела сопротивляться изменению скорости тела называется инерцией. Сила, с которой происходит сопротивление, называется силой инерции. Основной закон динамики: Ускорение, сообщаемое телу, пропорционально действующей на тело силе и направлено по этой силе.   Масса является мерой инертности. Закон действия и противодействия сил: Силы взаимодействия 2-х материальных точек равны по модулю и направлены в противоположную сторону по линии действия этих сил.  Закон независимости действия сил: Ускорение материальной точки, находящейся под действием нескольких сил равно геометрической сумме тех ускорений, которые точка могла бы получиться под действием каждой силы по отдельности.     32. Дифференциальные уравнения движения точки.   Дифференциальное уравнения движения материальной точки в векторном пространстве.  Дифференциальное уравнения в Декартовой системе координат.   |