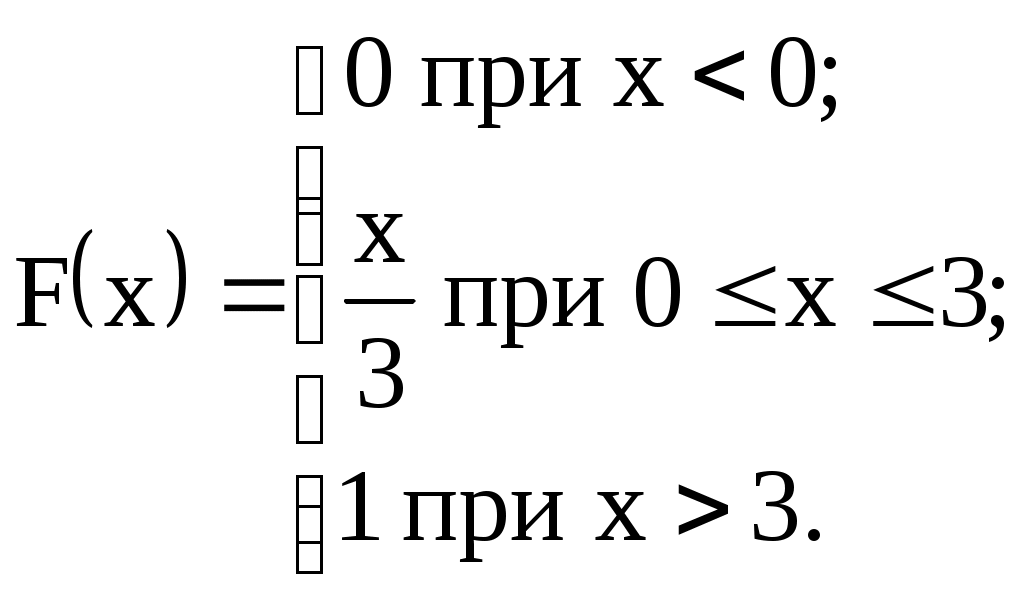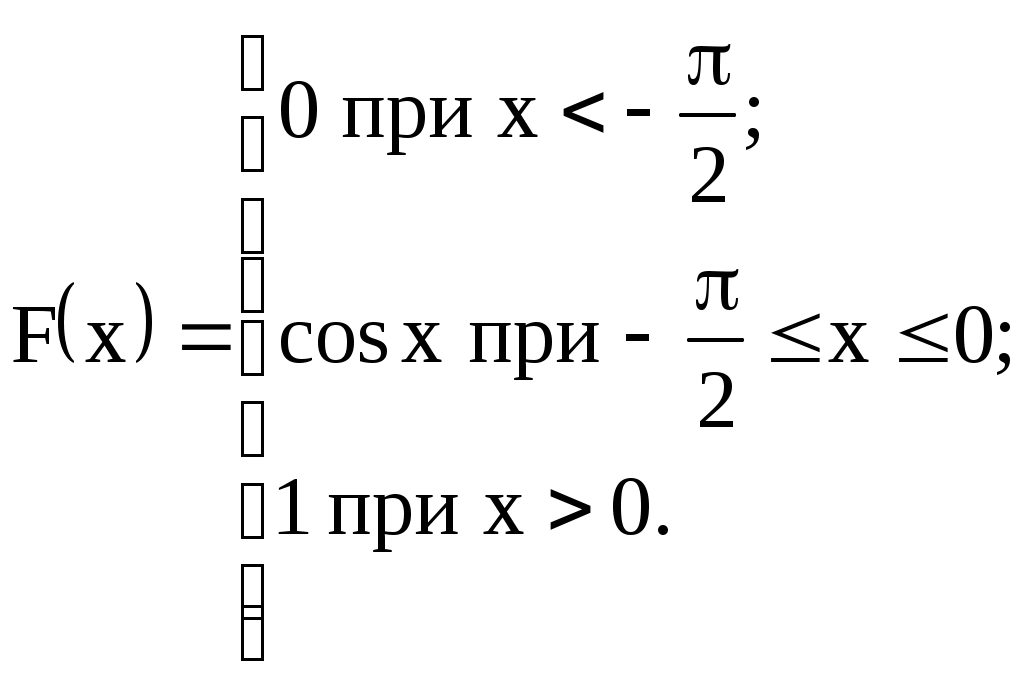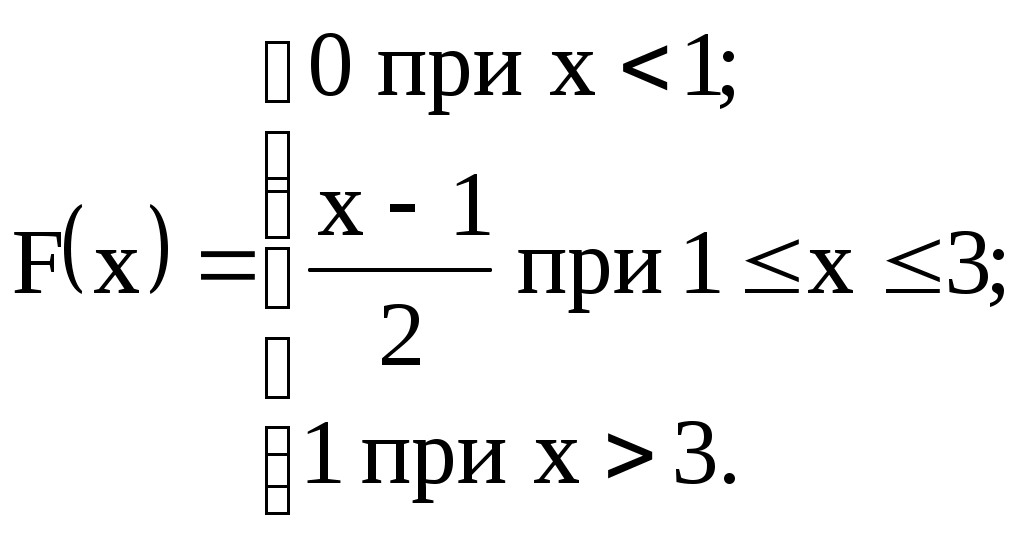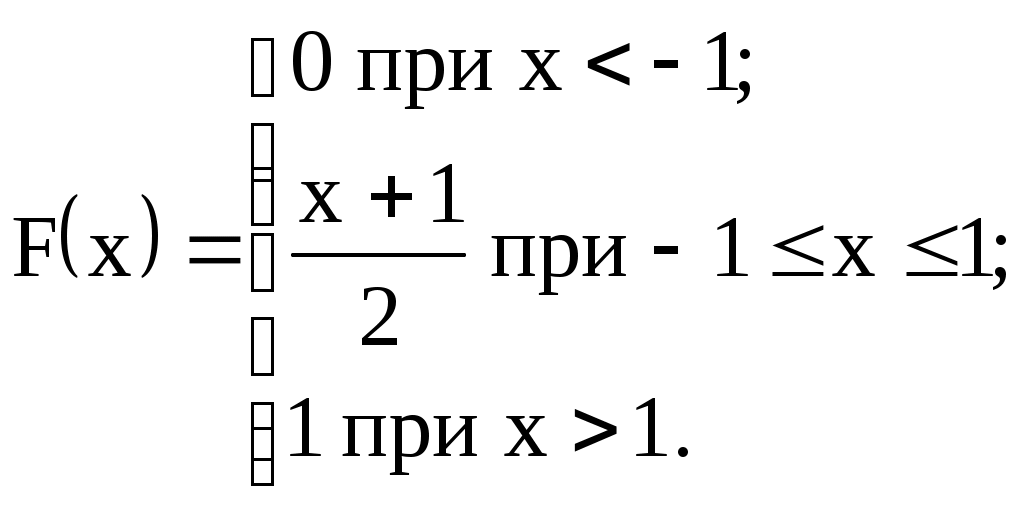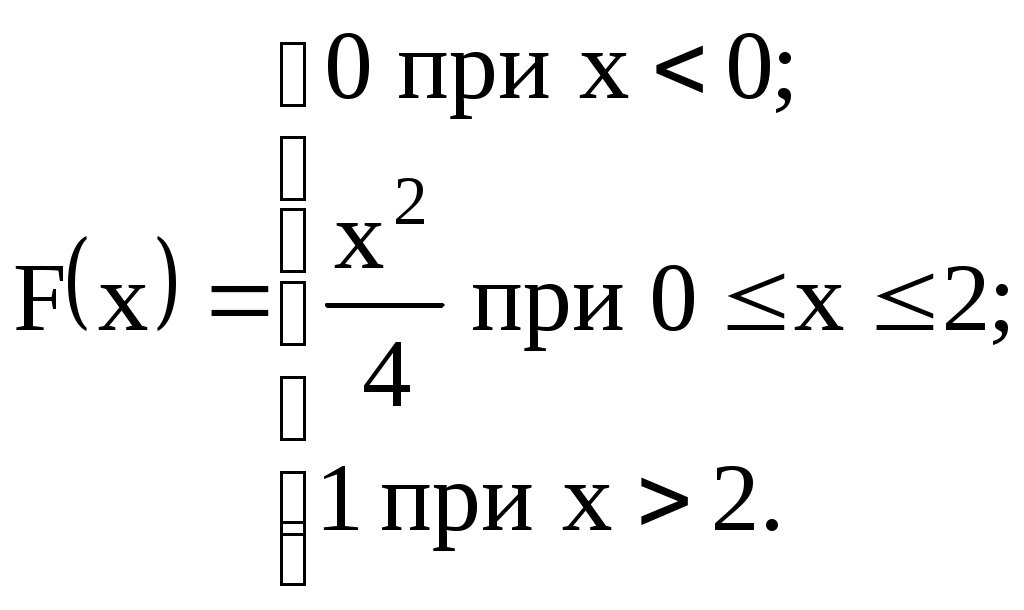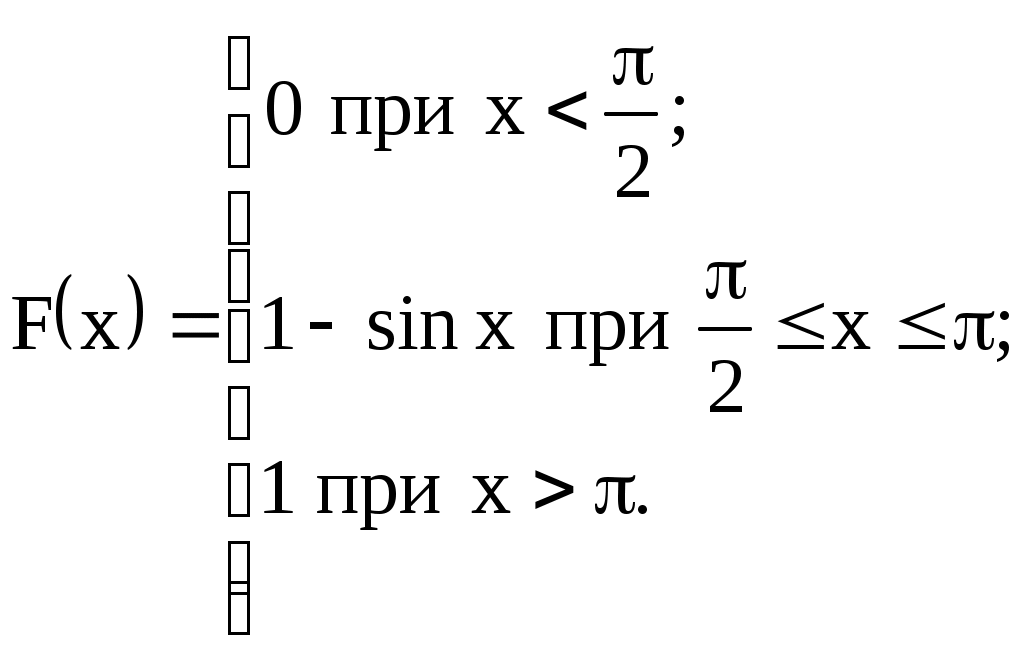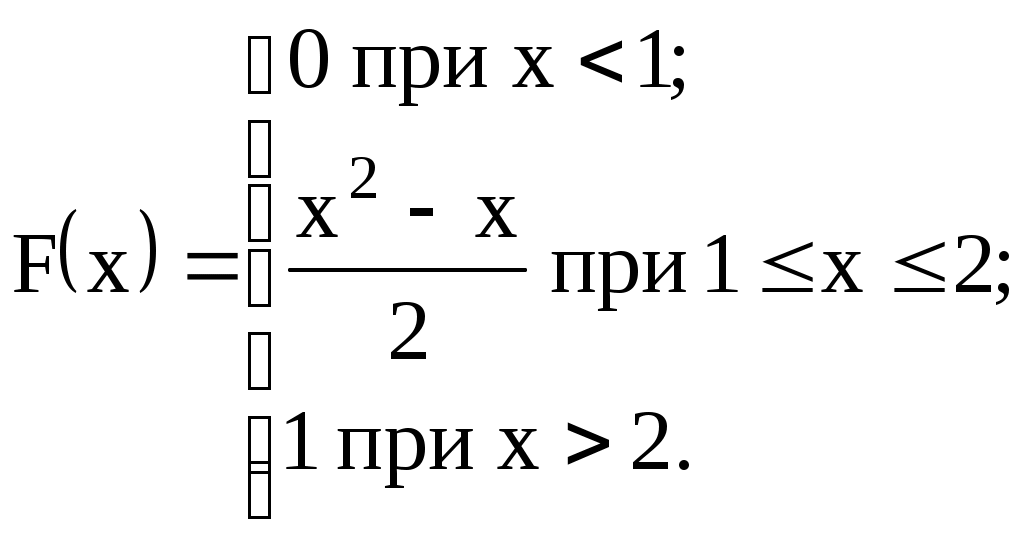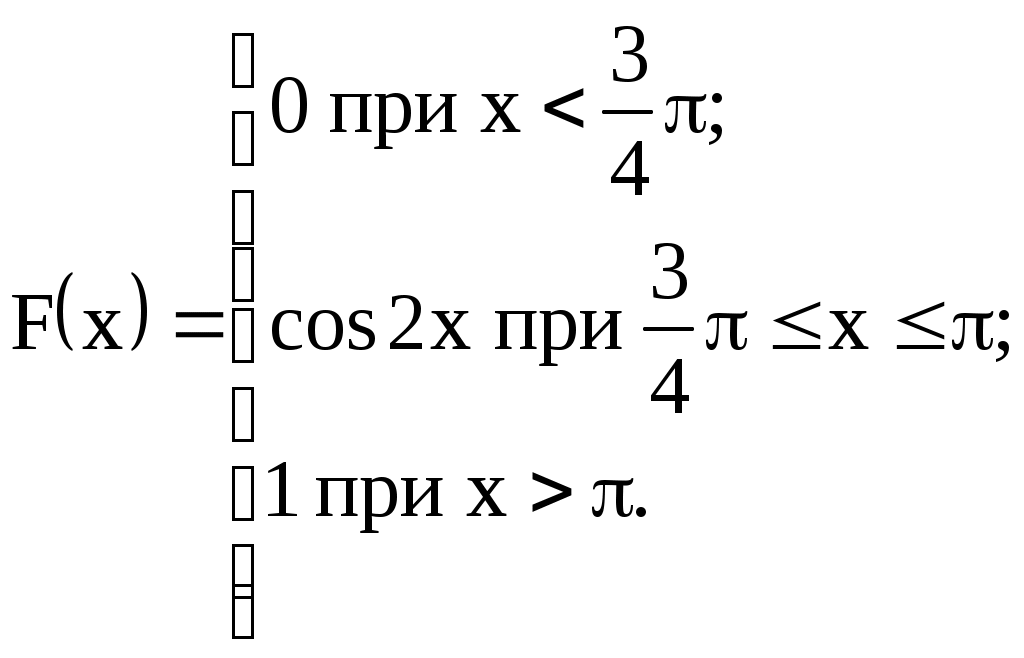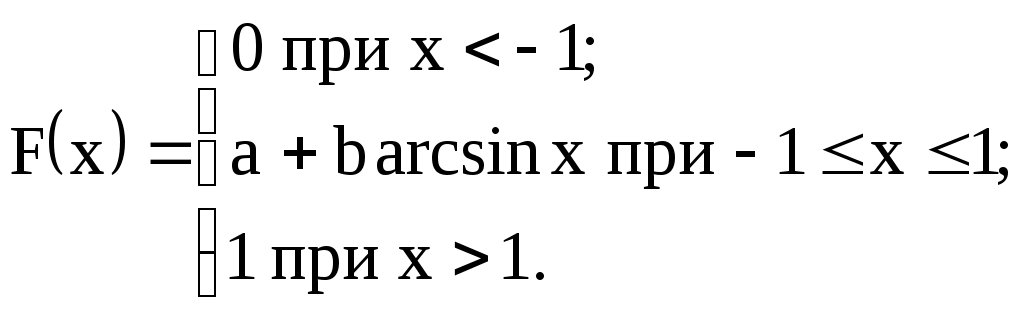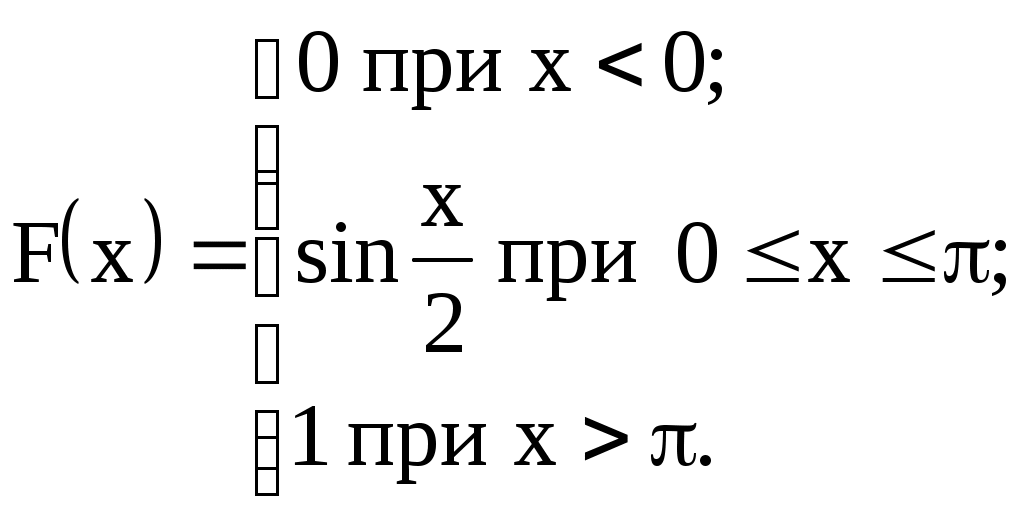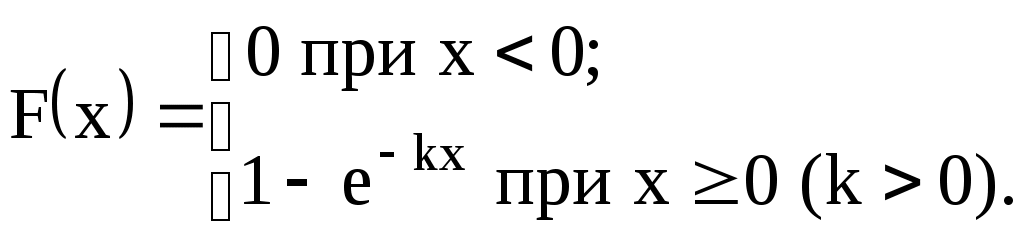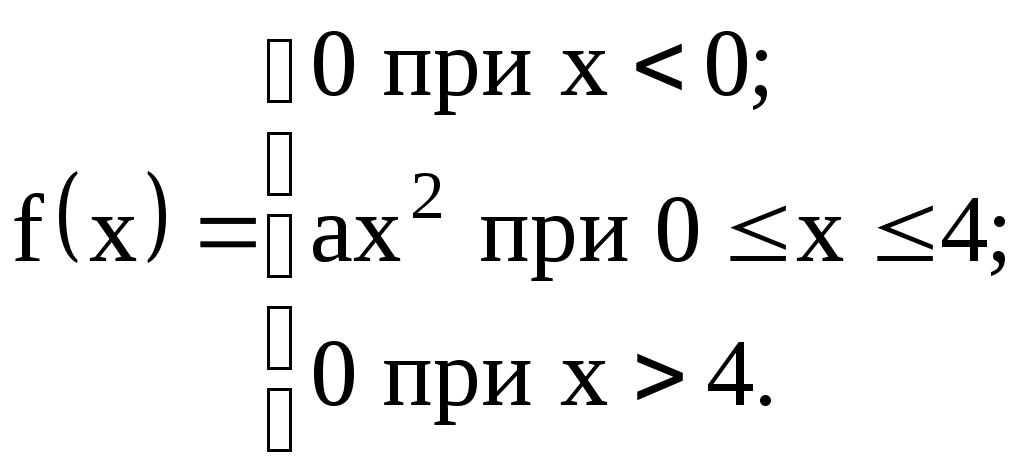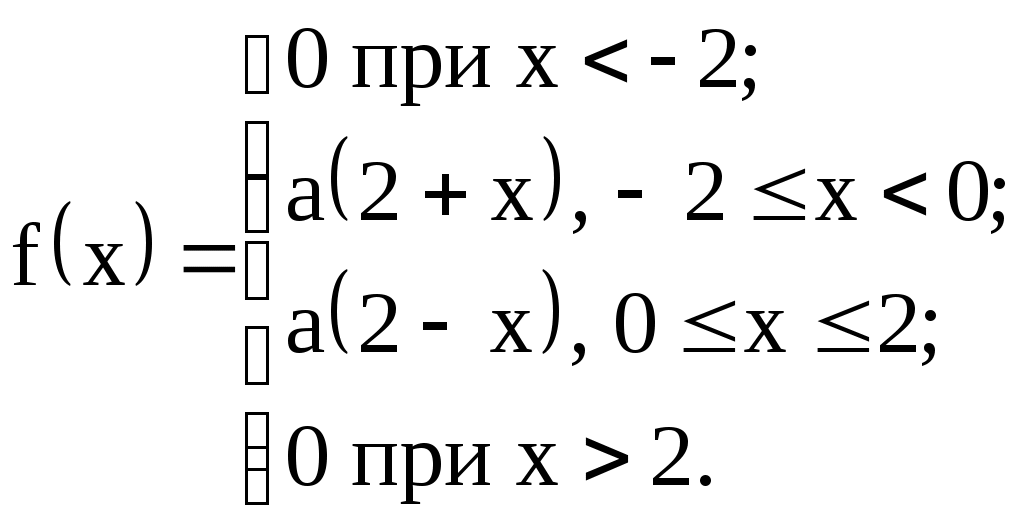теория вероятностей. Теория вероятностей.ТРЗ. Теория вероятностей
 Скачать 282.5 Kb.
|
|
Задание №4. Закон распределения и числовые характеристики дискретных случайных величин 1) Изделия в количестве 3 штук испытываются при перегрузочных режимах. Вероятность для каждого изделия пройти испытание равна 4/5. Найти функцию вероятности случайного числа Х изделий, выдержавших испытание. Найти М(Х) и D(Х). 2) Стрелок ведёт стрельбу по мишени до первого попадания, имея боезапас 4 патрона. Вероятность попадания при каждом выстреле равна 0,6. Построить функцию распределения боезапаса, оставшегося неизрасходованным. Найти М(Х) и D(Х). 3) Производятся независимые испытания, в каждом из которых с вероятностью 0,8 может произойти некоторое событие А, общее число испытаний не превосходит четырёх. Построить функцию распределения случайной величины Х числа испытаний. Найти М(Х) и D(Х). 4) Производится 4 независимых опыта, в каждом из которых вероятность появления события А равна 0,3. Построить функцию распределения числа Х появления события А. Найти М(Х) и D(Х). 5) Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить функцию распределения числа Х выбитых очков. Найти М(Х) и D(Х). 6) Из партии, содержащей 100 изделий, среди которых 10 дефектных, выбраны случайным образом 3 изделия для проверки качества. Построить функцию распределения случайного числа Х дефектных изделий в выборке. Найти М(Х) и D(Х). 7) Производится три броска мяча в корзину. Вероятность попадания в корзину при каждом броске равна 0,3. Построить функцию распределения случайного числа Х попаданий мяча в корзину. Найти М(Х) и D(Х). 8) Из урны, в которой лежат 5 чёрных и 3 белых шара, последовательно вынимают шары до тех пор, пока не появится чёрный шар. Найти функцию распределения случайного числа Х вынутых при этом белых шаров, т.е. числа белых шаров, вынутых до первого чёрного шара. Найти М(Х) и D(Х). 9) Из урны, в которой лежат 5 чёрных и 3 белых шара, вынимают 4 шара. Построить функцию распределения случайного числа Х вынутых белых шаров. Найти М(Х) и D(Х). 10) Два баскетболиста поочерёдно бросают мяч в корзину до тех пор, пока один из них не попадёт, но не более трёх раз. Построить функцию распределения случайного числа бросков, производимых каждым из баскетболистов, если вероятность попадания для первого из них равна 0,4, а для второго – 0,6. Найти М(Х) и D(Х). 11) Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все 4 патрона). Построить функцию распределения случайного числа Х израсходованных патронов при условии, что вероятность попадания при каждом выстреле равна 0,8. Найти М(Х) и D(Х). 12) Стрелок делает 3 выстрела по мишени. Вероятность попадания при каждом выстреле равна 2/3. Построить функцию распределения случайного числа Х попаданий. Найти М(Х) и D(Х). 13) Игральная кость бросается 3 раза. Построить функцию распределения для возможного числа Х выпадений "шестёрки". Найти М(Х) и D(Х). 14) В стопке тетрадей находятся 6 тетрадей в клетку и 3 тетради в линию. Наудачу взяты 3 тетради. Построить функцию распределения случайного числа Х тетрадей в линию в отобранной группе. Найти М(Х) и D(Х). 15) Вероятность детали быть бракованной равна 1/5. Взято на пробу 3 детали. Построить функцию распределения для случайного числа Х бракованных изделий в пробе. Найти М(Х) и D(Х). 16) Баскетболист производит 3 броска мячом в корзину с вероятностью попадания при каждом броске 0,6. Каждое попадание приносит команде 2 очка. Построить функцию распределения для возможного числа Х очков, принесённом баскетболистом команде. Найти М(Х) и D(Х). 17) В коробке 3 красных и 2 синих карандаша. Производится вынимание до появления синего карандаша. Построить функцию распределения случайного числа Х выниманий. Найти М(Х) и D(Х). 18) Из большой партии изделий взяли на проверку 4 детали. Доля дефектных деталей во всей партии 20%. Построить функцию распределения для случайного числа Х дефектных деталей в пробе. Найти М(Х) и D(Х). 19) Три орудия делают один залп по общей цели. Вероятность попадания в цель для первого орудия равна 0,6, для второго – 0,8, для третьего 0,7. Построить функцию распределения для случайного числа Х попаданий в цель при залпе. Найти М(Х) и D(Х). 20) Карточки с цифрами 1, 2, 3, ,4 ,5 перемешаны, а затем случайным образом вынимаются до появления чётной цифры. Построить функцию распределения для случайного числа Х выниманий. Найти М(Х) и D(Х). 21) На месте происшествия оказались 6 женщин и 4 мужчины. Для составления протокола случайным образом отобраны 4 человека. Построить функцию распределения для случайного числа Х мужчин, вошедших в группу для составления протокола. Найти М(Х) и D(Х). 22) Монета бросается до появления "герба" но не более 5 раз. Построить функцию распределения для случайного числа Х бросаний (т.е. числа бросаний до первого появления "герба"). Найти М(Х) и D(Х). 23) На пути движения автомашины 4 светофора, на которых с равной вероятностью может быть разрешающий или запрещающий сигнал. Построить функцию распределения для возможного числа Х остановок автомашины у светофора. Найти М(Х) и D(Х). 24) На остановке стояли четверо мужчин и три женщины. В подошедшее такси случайным образом сели четыре человека. Построить функцию распределения для случайного числа Х женщин, севших в такси. Найти М(Х) и D(Х). 25) Игрок А играет с игроком В либо до первого выигрыша игрока А либо 4 партии. Составить функцию распределения для случайного числа Х игр, если вероятность выигрыша игрока А равна 0,6. Найти М(Х) и D(Х). 26) Вероятность того, что в библиотеке необходимая курсанту книга свободна, равна 0,3. Составить функцию распределения случайного числа Х библиотек, которые посетит курсант в поисках книги, если в городе 4 библиотеки. 27) Три стрелка стреляют по одной цели. Вероятность попадания в цель для первого стрелка равна 0,5, для второго – 0,7, для третьего – 0,4. Составить функцию распределения для случайного числа Х попаданий в цель при одном залпе. Найти М(Х) и D(Х). 28) Испытывается устройство, состоящее из трёх независимо работающих приборов. Вероятности отказа работы приборов таковы: р1 = 0,3; р2 = 0,4; р3 = 0,5. Составить функцию распределения для случайного числа Х отказавших приборов. Найти М(Х) и D(Х). 29) Монета бросается 4 раза. Построить функцию распределения случайного числа Х выпадений "герба". Найти М(Х) и D(Х). 30) В ящике 7 белых и 3 чёрных шара. Наугад вынуто 3 шара. Составить функцию распределения для случайного числа Х чёрных шаров в отобранной партии. Найти М(Х) и D(Х). Задание №5. Функции распределения и числовые характеристики непрерывных случайных величин 1) Случайная величина X задана плотностью распределения вероятностей: 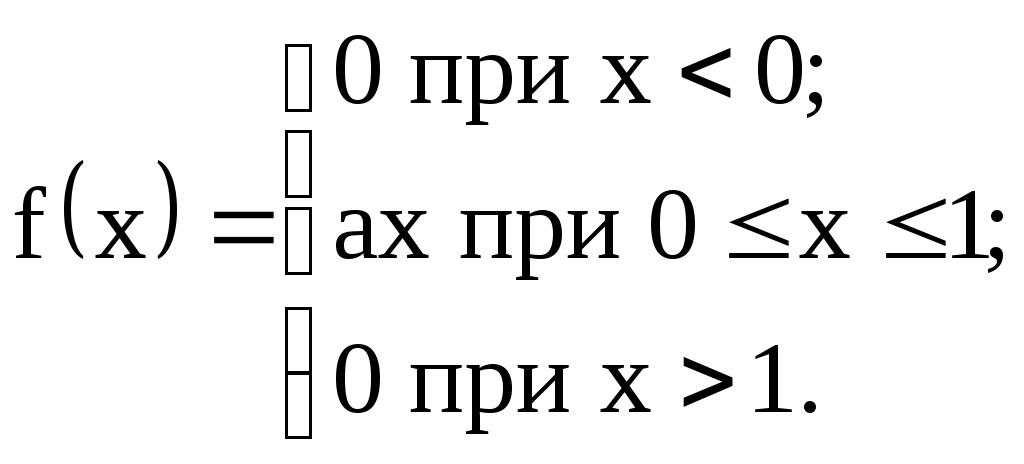 Найти коэффициент "а", F(x), M(X), D(X),  .2) Дана функция f(x) = axe-кx (к > 0), (  ). При каком значении "а" эта функция может быть принята за плотность вероятностей случайной величины Х? Найти М(Х) и D(Х).3) Случайная величина Х задана интегральной функцией распределения: 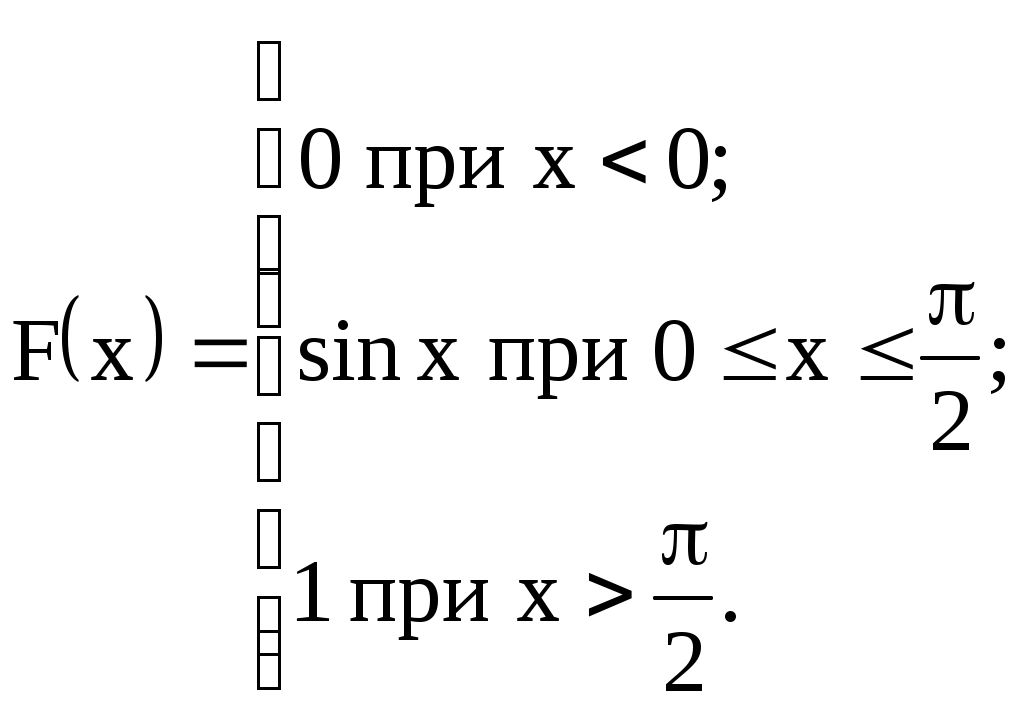 Найти М(Х), D(Х). 4) Случайная величина задана плотностью распределения: 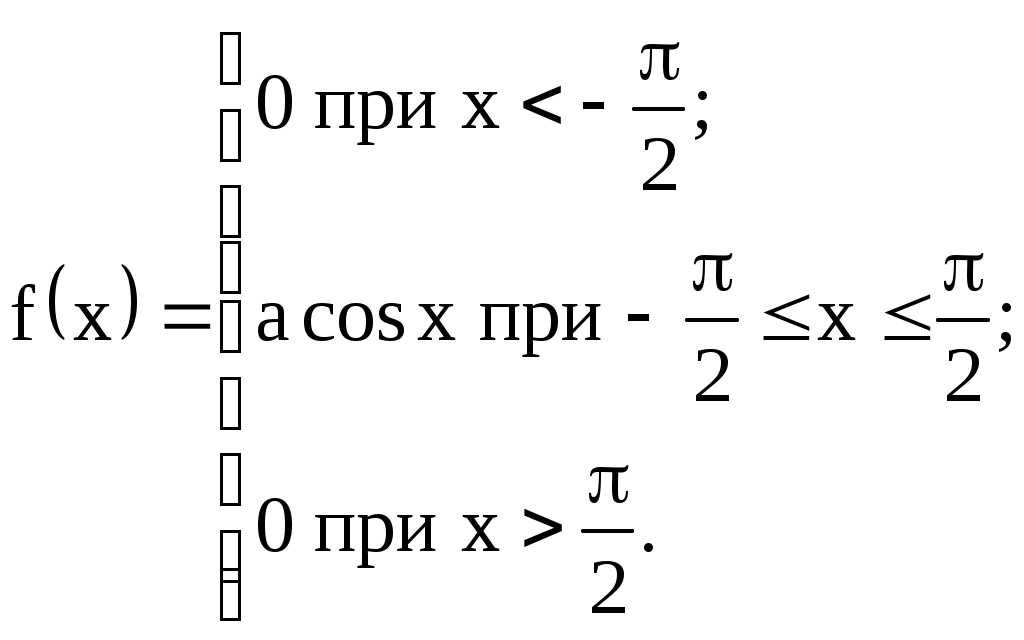 Найти коэффициент "а", F(x), M(X), D(X). 5) Функция распределения случайной величины Х задана выражением: 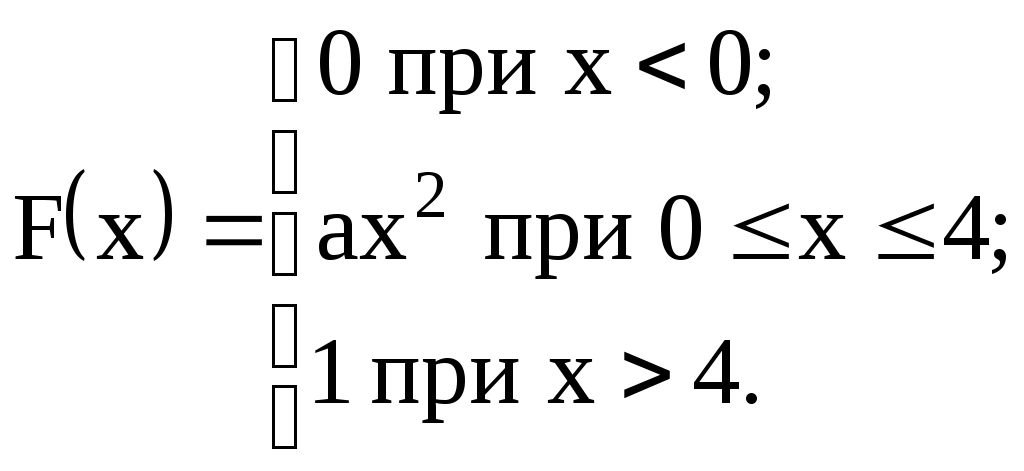 Найти коэффициент "а", M(X), D(X),  .6) Дана интегральная функция распределения случайной величины Х: 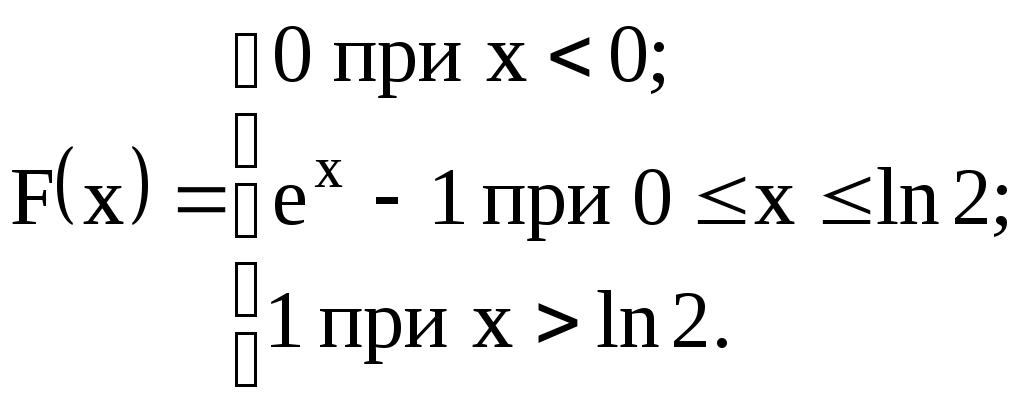 Найти M(X) и D(X). 7) Дана интегральная функция распределения случайной величины Х: 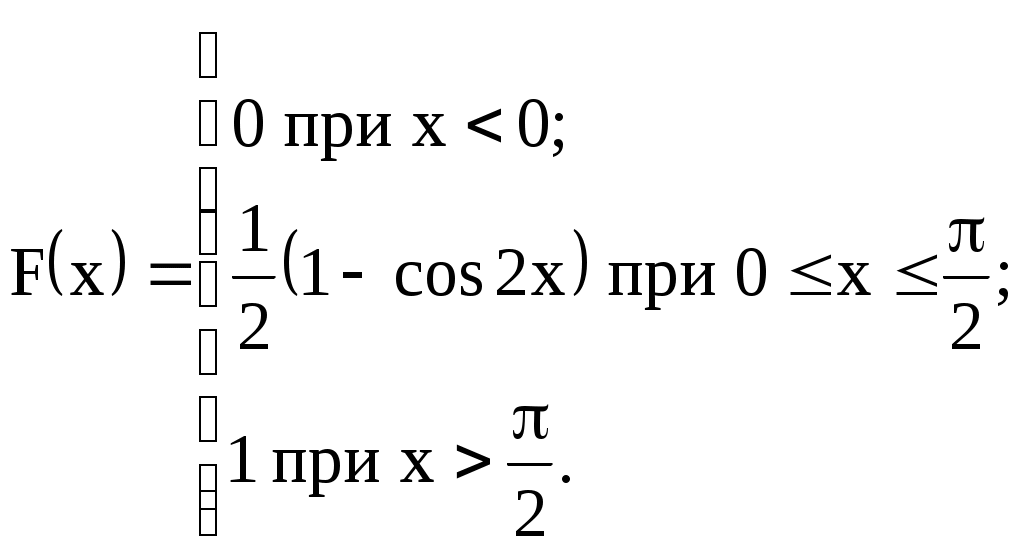 Найти M(X), D(X),  .8) Дана функция плотности распределения случайной величины Х: 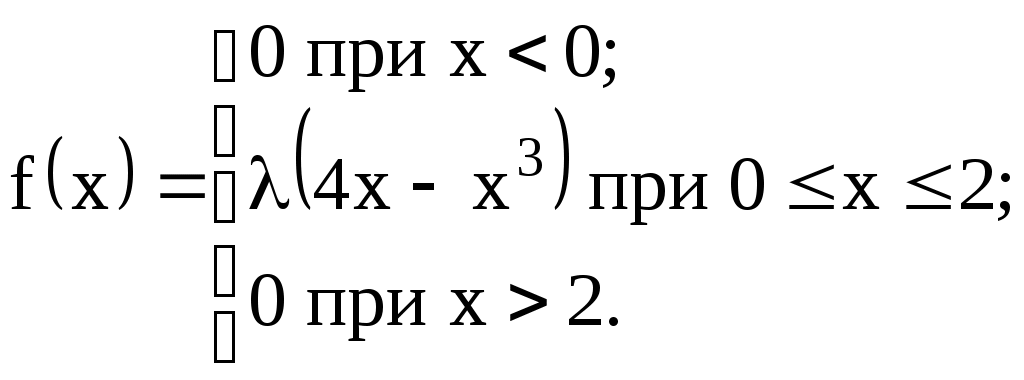 Найти значение "", M(X), D(X),  .
|
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, построить графики f(x) и F(x)
, F(x)