Териалы электронной техники

• Название: Териалы электронной техники
• Дата: 02.03.2022
• Размер: 2.56 Mb.
• Имя файла: MET_docx.doc
• Тип: Практикум; #379289
• страница: 2 из 10

Таблица 1.1

Материал (1…3)	R, Ом	b, мм	1, мм	R□ Ом

Таблица 1.2

Материал (6…10)	R, Ом	1, мм	D, мм	ρ, мкОм.м

Результаты измерений и геометрические размеры резисторов занести в табл.1.1 и табл. 1.2.

1.3.2. Определение температурных зависимостей сопротивления

проводников и термоЭДС

Измерить значения сопротивлений резисторов Rl, R2, R3 при комнатной температуре. Включить тумблер «Установка температуры» и установить регулятор температуры в положение «min».

После стабилизации температуры в термостате произвести измерение сопротивлений резисторовRl, R2, R3. При том же значении установившейся температуры, поставив переключатель мультиметра в режим измерения постоянного напряжения, измерить термоЭДС термопар медь–железо, медь–константан, медь–манганин.

Аналогичным образом провести измерения сопротивлений резисторов Rl, R2, R3 и термоЭДС всех термопар при других температурах вплоть до 200 °С. При каждом измерений термоЭДС термопар регистрировать температуру холодного спая термопары.

Таблица 1.3

	Никель			Медь			Константан
t, °C	R,Ом	ρ, Ом*м	αρ, К−1	R,Ом	ρ, Ом*м	αρ, К-1	R,Ом	ρ, Ом*м	αρ, К−1

Таблица 1.4

t гор, °C, °C	t хол, °C, °C	Δt, °C, °C	ΔU, мВ
			Медь–железо	Медь–константан	Медь–манганин

Результаты измерения сопротивлений записать в табл.1.3, а значения термоЭДС занести в табл.1.4. После окончания измерений регулятор температуры поставить в крайнее левое положение. Выключить термостат (нагрев).

1.4. Обработка результатов

1. По данным 1.3.1 рассчитать удельное сопротивление металлических проводников, используя соотношение:

ρ=RS/l,

где R – сопротивление образца; S – площадь поперечного сечения; l – длина проводника.

Рассчитать сопротивление квадрата поверхности металлических пленок

R_□ = Rb/l,

где R – сопротивление образца; b – ширина резистивного слоя; l – длина пленки (расстояние между контактными площадками).

Результаты занести в табл.1.1 и табл.1.2.

2. По данным табл.1.3 построить температурную зависимость сопротивления R=f(t) для исследованных материалов.

3. Рассчитать температурный коэффициент удельного сопротивления металлов и сплавов как

α_ρ=α_R+ α_l,

где α_Rиα_l – температурные коэффициенты сопротивления и линейного расширения соответственно.

Температурный коэффициент сопротивления при данной температуре рассчитать по выражению: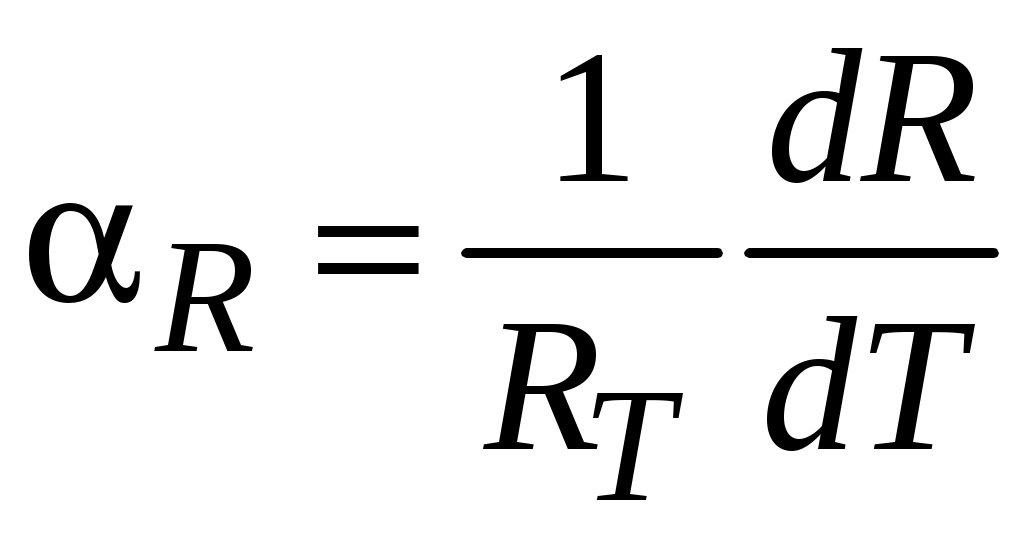

,

где R– сопротивление образца при данной температуре.
Значение производной dR/dT найти путем графического дифференцирования зависимости R(t). Для этого провести касательные к графику зависимости R(t) в точках, соответствующих выбранным температурам, и построить на них прямоугольные треугольники произвольных размеров. Искомую величину определить в виде отношения ΔR/Δt.

В случае, если зависимостьR(T) можно аппроксимировать линейной зависимостью, отношение ΔR/ΔT остается постоянным во всем интервале температур.

Температурные коэффициенты линейного расширения имеют следующие значения: для меди – 16,7^.10⁻⁶ К^-1; никеля – 12,8^.10⁻⁶ К⁻¹, константана – 17,0^.10⁻⁶ К⁻¹. Результаты расчетов занести в табл. 1.3.

4. По данным табл.1.3 построить зависимость α_ρ=f(t) для исследованных материалов.

5. Рассчитать зависимости удельного сопротивления и температурного коэффициента удельного сопротивления от состава для сплавов системы Cu-Ni при комнатной температуре.

Значения удельного сопротивления сплавов могут быть получены по приближенной формуле:

ρ_Cu-Ni = ρ_Niх_Ni + ρ_Сu (1−х_Ni) + С х_Ni(1−х_Ni), (1.2)

где С – постоянный коэффициент; х_Ni – содержание никеля в сплаве в относительных долях по массе; х_Ni + х_Cu =1.

Первые два слагаемых в формуле (1.2) характеризуют удельное сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов кристаллической решетки. Предполагается, что эти составляющие удельного сопротивления аддитивно зависят от состава. Третье слагаемое характеризует изменение остаточного сопротивления от состава.

.

Коэффициент «С» находят путем подстановки в (1.2) значения удельного сопротивления константана и соответствующего ему содержания никеля х_Ni = 0,4. Подставляя различные значения x_Ni в выражение (1.2), получают необходимое число точек для построения кривой ρ=f(x).

Значения удельного сопротивления меди, никеля и константана следует взять из справочной литературы.

Результаты расчетов занести в табл.1.5.

Таблица 1.5

хNi	0	0,2	0,4	0,6	0,8	1,0
ρ,мкОм∙м
αρ ,К−1

Значения температурного коэффициента удельного сопротивления сплавов Cu-Ni при различных содержаниях никеля могут быть приближенно рассчитаны по формуле: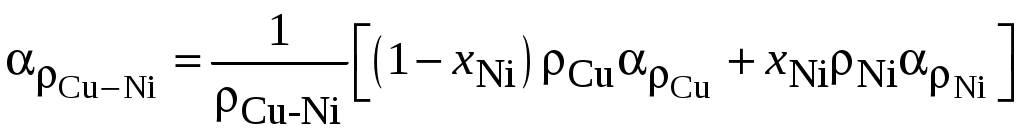

, (1.3)

где − удельное сопротивление сплава соответствующего состава, определенного по формуле (1.2).

Значения температурного коэффициента удельного сопротивления α_ρ меди и никеля при комнатной температуре следует взять из табл. 1.3.

Результаты расчета по 1.3 занести в табл. 1.5.

6. Построить зависимости удельного сопротивления сплава ρ_Cu-Ni и температурного коэффициента удельного сопротивления сплава α_ρ(х_Cu-Ni) от состава сплава по данным табл.1.5.

По оси абсцисс слева направо в линейном масштабе откладывать содержание никеля, а справа налево − содержание меди так, чтобы выполнялось соотношение x_Ni + x_Cu =1.

По оси ординат, построенной из точки х_Ni = 0 (х_Cu = 1), откладывать значения ρ, а по оси ординат, построенной из точки х_Ni = 1 (х_Cu = 0). откладывать значения α_ρ.

На графике α_ρ(х_Cu-Ni) помимо расчетных значений для х_Ni = 0,4 указать экспериментально найденное значение α_ρ константана (см. табл. 1.3).

7. Построить температурные зависимости термоЭДС ΔU( ) для исследованных термопар по данным табл. 1.4 .