Териалы электронной техники
 Скачать 2.56 Mb.
|
Таблица 3.3
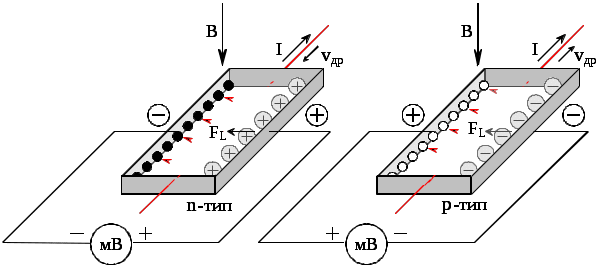
Исследования по п.п.3.3.1 и 3.3.2 провести для образцов 1 и 2. По окончании работы выключить лампу и измерительную установку. 3.4. Обработка результатов 1. По данным п. 3.3.1 вычислить проводимость полупроводника на свету для всех длин волн γс = 1/Rс. Результаты записать в табл. 3.1. 2. По выражению (3.1), вычислить фотопроводимость  , приняв темновое сопротивление Rт = 10 МОм. Результаты записать в табл. 3.1.3. Вычислить приведенную фотопроводимость (изменение проводимости полупроводника под действием единицы энергии падающего излучения)  .Результаты записать в табл. 3.1. 4. По данным табл. 3.1 построить спектральную зависимость фотопроводимости, откладывая по оси абсцисс значения λ, а по оси ординат относительную фотопроводимость  , где  – максимальное значение приведенной фотопроводимости для исследованного образца.5. Пользуясь графиком этой зависимости, определить красную границу λпор фоторезистивного эффекта. Так как экспериментальная характеристика имеет размытую длинноволновую область, принять λпор равной λ1/2, при которой фотопроводимость равна половине ее значения при λmax. По полученному значению λпор вычислить энергию активации фотопроводимости по формуле (3.2). 6. По данным п. 3.3.2 вычислить проводимость и фотопроводимость полупроводника для каждого значения ширины щели. Результаты записать в табл. 3.3. 7. По данным табл. 3.3 построить световую характеристику, откладывая по оси абсцисс lg (d/dmax), где dmax – максимальная ширина щели, а по оси ординат lg γф. 3.5. Контрольные вопросы 1. Каковы физические основы изменения проводимости полупроводников под действием света? 2. Каков принцип увеличения фоточувствительности полупроводникового материала к воздействующему облучению. 3. Как объяснить ход спектральной характеристики полупроводников под действием света? 4. Как объяснить ход световой характеристики полупроводника? 5. Чем объяснить различие λ1/2 для двух различных полупроводников? 4. ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА ЦЕЛЬ РАБОТЫ: определение с помощью эффекта холла концентрации и подвижности носителей заряда в полупроводниках. 4.1. Основные понятия и определения Физические явления, возникающие в полупроводнике при одновременном воздействии на него электрического и магнитного полей, называют гальваномагнитными эффектами. Среди гальваномагнитных эффектов одним из важнейших является эффект Холла. Сущность его заключается в возникновении поперечной разности потенциалов в пластине полупроводника, по которой проходит электрический ток, при помещении ее в магнитное поле, направление которого перпендикулярно направлению тока. Возникающая на боковых гранях пластины разность потенциалов, назваемая ЭДС Холла (UН), перпендикулярна и направлению тока, и напряженности магнитного поля. Появление ЭДС Холла обусловлено тем, что на носители заряда, движущиеся со средней скоростью v направленного движения (скоростью дрейфа), в магнитном поле с индукцией В действует сила Лоренца, отклоняющая их к одной из боковых граней пластины FL = e[vB]. Следует отметить, что скорость v – скорость направленного движения носителей заряда (скорость дрейфа), обусловленная действием на носители заряда силы электрического поля FE =± eE, где Е – напряженность электрического поля. Так как заряды электронов и дырок имеют противоположные знаки, дрейфуют эти носители в противоположных направлениях. Сила Лоренца, действующая на дрейфующие электроны и дырки, отклоняет их в одну и ту же сторону: FL = ±e[±vB]. (4.1) Направление действия силы Лоренца определяется по известному правилу левой руки, если относить его к техническому направлению тока. Отсюда следует, что направление силы Лоренца не зависит от знака носителей заряда, а определяется лишь направлениями электрического и магнитного полей. Поэтому полярность ЭДС Холла в полупроводнике n-типа оказывается противоположной полярности, получаемой в материале р-типа, что и используется для определения типа электропроводности полупроводников (рис. 4.1). В условиях термодинамического равновесия полупроводник нейтрален. Это состояние описывается уравнением электронейтральности:  , где n0, p0 – концентрации подвижных электронов и дырок соответственно,  – концентрация ионизированных доноров,  – концентрация ионизированных акцепторов. При воздействии только электрического поля подвижные электроны и дырки направленно дрейфуют, а ионы остаются в местах своего расположения в кристаллической решетке полупроводника, их направленная скорость равна нулю. Очевидно, что дрейф подвижных носителей заряда не нарушает условие электронейтральности: в любой точке полупроводника  .
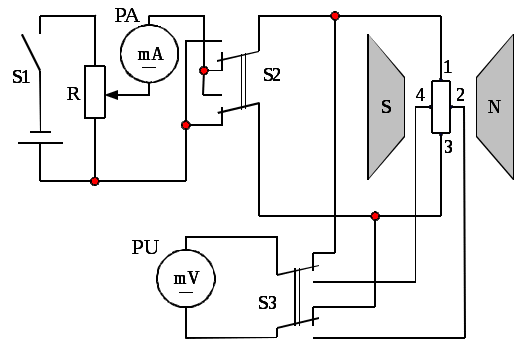
Подчеркнем, что сила Лоренца (4.1) действует лишь на направленно движущиеся носители заряда, смещая их в направлении, перпендикулярном направлениям напряженностей приложенных электрического (Е) и магнитного (В) полей. «Неподвижные» ионизированные атомы (примесные или собственные) остаются на своих местах, т. е. сила Лоренца обуславливает пространственное перераспределение носителей зарядов в полупроводнике (рис. 4.1). Такое перераспределение приводит к возникновению поперечного электрического поля (холловского поля)  . Под действием этого поля возникает направленное движение подвижных носителей заряда со скоростью  и плотностью  в направлении противоположном движению носителей заряда под действием силы Лоренца с плотностью  . В стационарных условиях устанавливается динамическое равновесие:  .Очевидно, чем больше подвижных носителей заряда в полупроводнике, тем больше  , тем меньше эффект Холла, характеризующийся величиной ЭДС Холла (UН): , (4.2)где I – сила тока, текущего через образец; В – величина индукции магнитного поля;  δ – толщина образца; RH – параметр, называемый постоянной Холла – константа полупроводника, характеризующая реакцию коллектива подвижных носителей заряда на одновременное воздействие электрического и магнитного полей, приложенных во взаимно перпендикулярных направлениях. В полупроводнике n-типа  ,в полупроводнике p-типа (4.3) 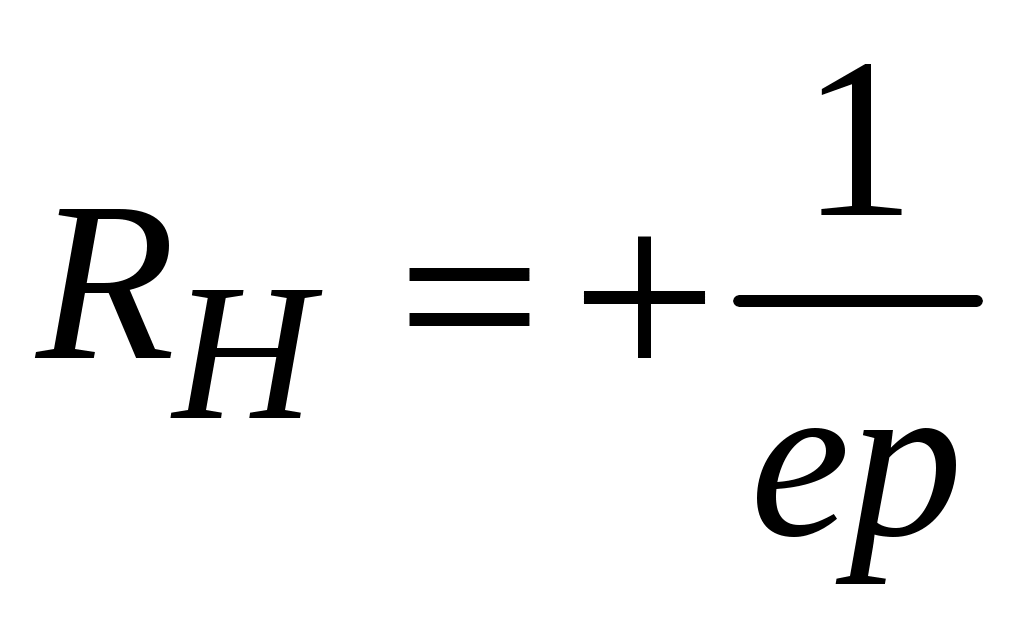 .Выражения (4.3), являются приближенными, поскольку в них не учитывается вклад механизмов рассеяния подвижных носителей заряда. По результатам измерения ЭДС Холла можно определить не только знак носителей заряда, но и рассчитать их концентрацию, а при известном значении удельной проводимости полупроводника найти и подвижность носителей заряда: 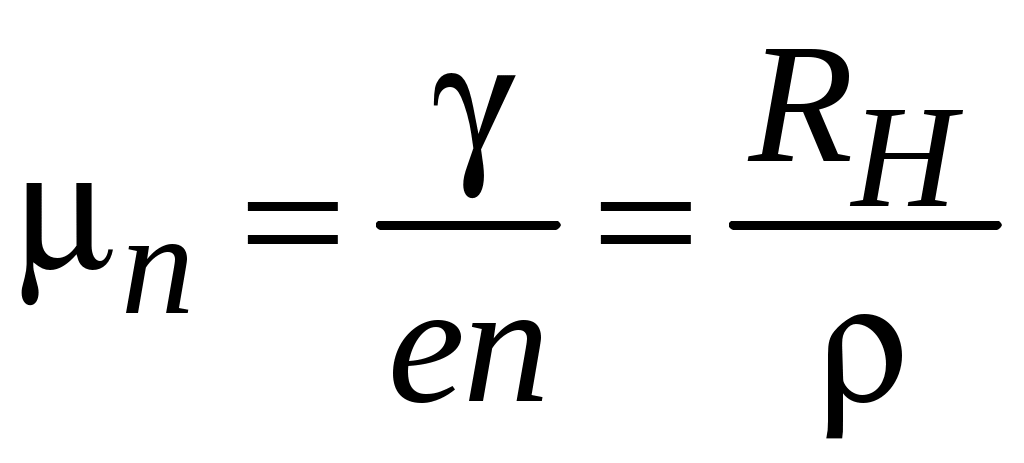 Как видно из уравнений (4.3) значение RHзависит от концентрации носителей заряда. И чем меньшее удельное сопротивление имеет полупроводник, тем менее выражен в нем эффект Холла. Измеряя ЭДС Холла в некотором диапазоне температур, получают экспериментальные данные для построения зависимости концентрации носителей заряда от температуры, по которой можно вычислить энергию ионизации доноров или акцепторов, ширину запрещенной зоны, а также концентрацию электрически активной примеси. Если при этом одновременно определять удельное сопротивление материала, то можно найти температурную зависимость подвижности носителей заряда. Эффект Холла интересен как явление, которое лежит в основе принципа действия ряда полупроводниковых приборов, достаточно широко применяемых в технике. К их числу относятся, в частности, измерители магнитной индукции, бесконтактные измерители тока, фазочувствительные детекторы, анализаторы спектра, модуляторы и др. 4.2. Описание установки Исследование параметров полупроводниковых материалов с помощью эффекта Холла осуществляется на установке, схема которой представлена на рис. 4.2. Измерения производятся на постоянном токе в постоянном магнитном поле. Схема позволяет одновременно определять ЭДС Холла и удельную проводимость образцов. Величина тока, протекающего через образец, регулируется потенциометром R и фиксируется миллиамперметром РА. Для изменения направления тока предусмотрен переключатель S2. В работе измеряется как поперечная разность потенциалов U24, так и продольная разность потенциалов U13. Их измерение производится вольтметром PU в зависимости от положения переключателя S3.
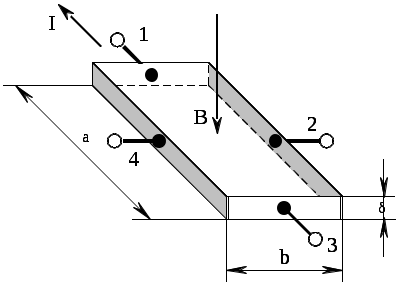
Исследуемые образцы представляют собой пластины полупроводников, имеющие по четыре электрода: 1, 3 – для измерения токов и напряжений; 2, 4 – для снятия ЭДС Холла. Форма и геометрические размеры образцов указаны на рис. 4.3 и в табл. 4.1.
Таблица 4.1
4.3. Проведение измерений Включить установку в сеть. Подключить образец полупроводника 1 к источнику постоянного тока ключом S1. Резистором R установить значение тока через образец, равное 4 мА. Поставив переключатель S3 в положение 1, измерить напряжение U13. При том же значении тока измерить U24, переведя переключатель S3 в положение 2. Для исключения возможной погрешности значение каждого из этих напряжений следует брать как среднее из двух измерений при противоположных направлениях тока, протекающего через образец. Изменить направление тока через образец, переключателем S2 и повторить измерения U13 и U24. В табл. 4.2 записать среднеарифметические значения результатов измерений U13 и значение ЭДС Холла, вычисленное как:  .Таблица 4.2
Повторить измерения и соответствующие вычисления при токах через образец, равных 8, 12, 16, 20 мА В том же порядке провести исследования образцов с номерами 2, 3, 4, 5. 4.4. Обработка результатов 1. Вычислить магнитную индукцию из соотношения B = UН /SB при протекании тока 20 мА через образец 1, магнитная чувствительность которого SB = 100 мкВ/мТл. 2. Для каждого из исследуемых образцов по полученным экспериментальным данным построить зависимости  , для всех образцов экстраполировать их прямолинейно. 3. Вычислить: коэффициент Холла RH, пользуясь выражением (4.2) при токе I = 5 мА и соответствующем ему значении  , взятом на прямых для каждого из образцов;удельную проводимость полупроводника: 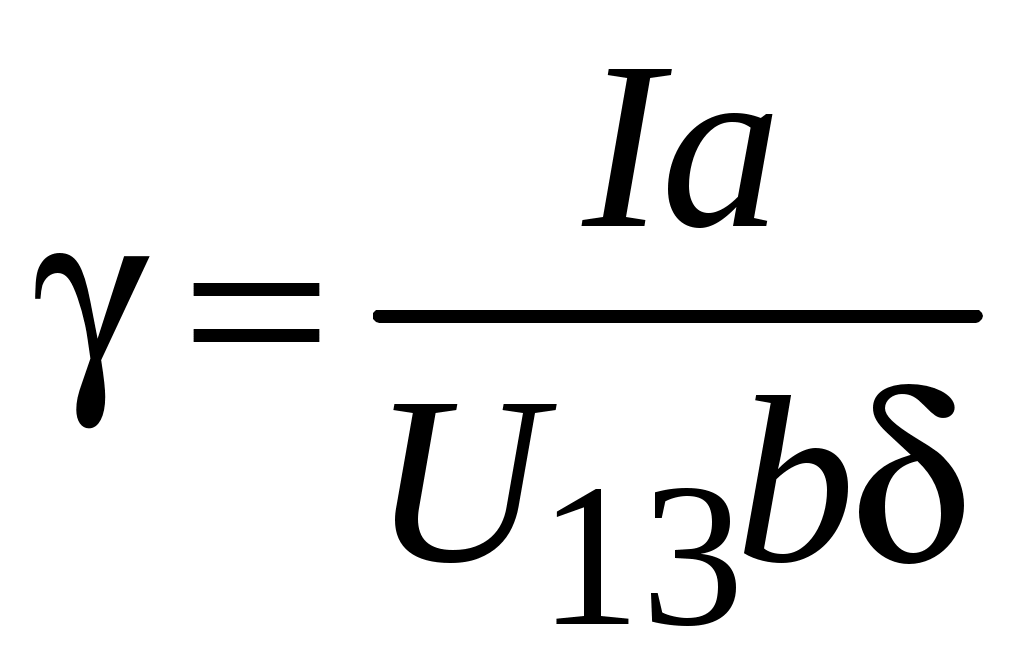 ;подвижность носителей заряда в полупроводнике:  ;концентрацию основных носителей заряда в полупроводнике в соответствии с 4.3: 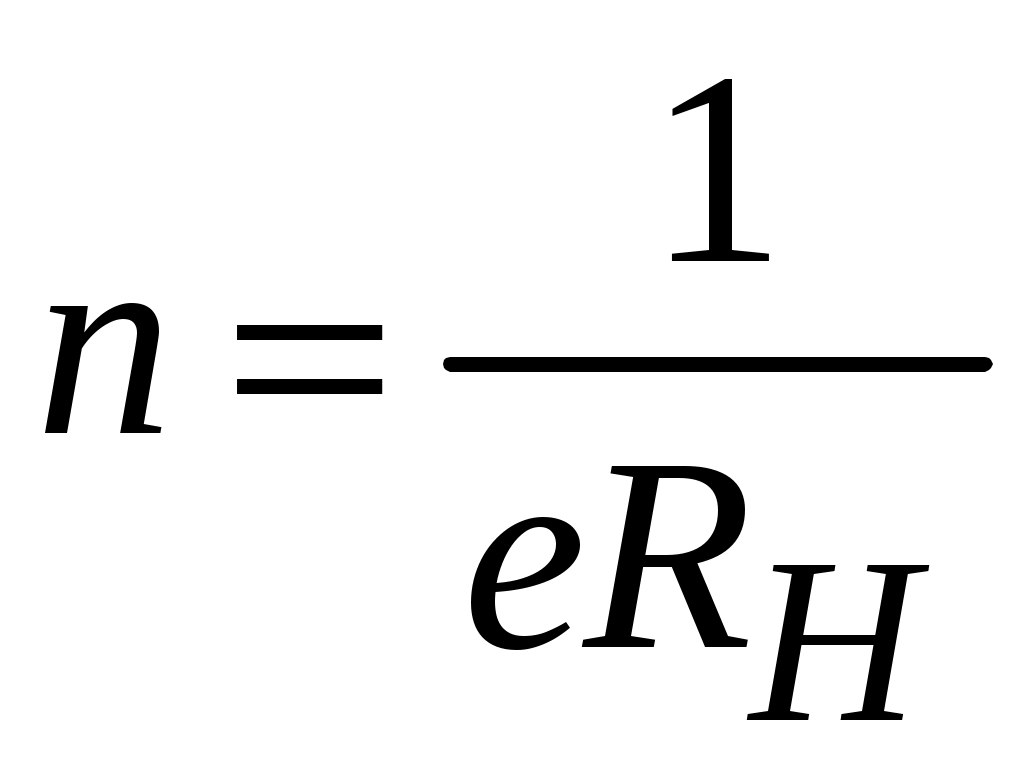 .Результаты расчета параметров полупроводников занести в табл. 4.2. 4.5. Контрольные вопросы 1. В чем заключается сущность эффекта Холла? 2. От каких факторов зависит ЭДС Холла? 3. Какие физические параметры полупроводниковых материалов можно определить с помощью эффекта Холла? 4. Что понимается под коэффициентом Холла? 5. Как определяется направление смещения носителей заряда под действием магнитного поля? 6. Какие материалы используются для изготовления датчиков Холла? 5. ИССЛЕДОВАНИЕ СВОЙСТВ ДИЭЛЕКТРИЧЕСКИХ МАТЕРИАЛОВ ЦЕЛЬ РАБОТЫ: исследование температурных зависимостей емкостей и тангенса угла диэлектрических линейных и нелинейных диэлектриков. 5.1. Основные понятия и определения Диэлектрики – это материалы или среды с удельным сопротивлением более 108 Ом∙м, в которых при приложении электрического поля возникает эффект поляризации. Поляризация может быть вызвана упругим смещением и деформацией электронных оболочек под действием поля (электронная поляризация), ориентацией дипольных молекул (дипольно-релаксационная поляризация), смещением ионов (ионная и ионно-релаксационная поляризация), упорядочением атомных групп (доменов) , обладающих дипольным моментом (спонтанная поляризация). Электронная и ионная поляризации устанавливаются практически мгновенно. Остальные механизмы поляризации относятся к замедленным видам. В процессе поляризации диэлектрик приобретает электрический момент, на его поверхностях образуются связанные заряды, на обкладках удерживается дополнительный заряд. В результате емкость конденсатора возрастает. Состояние диэлектрика, характеризующееся наличием электрического момента у любого элемента его объема, называют поляризованностью. Относительная диэлектрическая проницаемость характеризует способность различных диэлектриков поляризоваться в электрическом поле: ε = Сд/С0 , где Сд – емкость конденсатора с диэлектриком; С0 – емкость того же конденсатора в вакууме. В общем случае диэлектрическая проницаемость зависит от температуры и частоты электрического поля. Характер зависимости определяется присущими диэлектрику механизмами поляризации. При включении конденсатора под напряжение в нем наблюдаются потери электрической энергии, приводящие к его разогреванию. Потери энергии складываются из потерь в диэлектрике и потерь в проводящих частях конденсатора. Диэлектрическими потерями (потерями энергии в диэлектрике) называют электрическую мощность, затрачиваемую на нагрев диэлектрика, находящегося в электрическом поле. Различают два основных вида диэлектрических потерь: потери на электропроводность и релаксационные потери. Потери на электропроводность обнаруживаются в диэлектриках, имеющих заметную электропроводность, объемную или поверхностную, и наблюдаются во всех диэлектриках, как на постоянном, так и на переменном напряжении, причем являются преобладающими при низких частотах и при повышенных температурах. Релаксационные потери обусловлены активными составляющими поляризационных токов. Они характерны для диэлектриков с замедленными механизмами поляризации, когда сказывается отставание поляризации от изменения поля. Полные потери в участке изоляции с емкостью С при воздействии напряжения U с угловой частотой ω Ра=U2ωCtg δ , где δ – угол диэлектрических потерь. Углом диэлектрических потерь δ называют угол, дополняющий до 90° угол сдвига фаз φ между током и напряжением в емкостной цепи. В случае идеального диэлектрика вектор тока в такой цепи опережает вектор напряжения на угол π/2; при этом угол δ равен нулю. Чем больше рассеиваемая в диэлектрике мощность, тем меньше угол сдвига фаз φ и тем больше угол диэлектрических потерь δ и соответственно tg δ. Параметр tg δ характеризует способность диэлектрика рассеивать энергию в электрическом поле и, очевидно, определяет диапазон частот, в котором возможно использование конденсатора с данным диэлектриком. Емкость конденсатора С определяется как отношение накопленного в нем заряда Q к напряжению U, приложенному к электродам, и зависит от конструкции и геометрических размеров конденсатора, а также от диэлектрической проницаемости диэлектрика. Емкость плоского конденсатора определяется выражением:  , (5.1)где ε0 = 8,85∙10−12 Ф/м – электрическая постоянная; ε – относительная диэлектрическая проницаемость диэлектрика; S – площадь электродов, h – толщина диэлектрика, заключенного между электродами. В случае квадратных электродов S = l2, где l – сторона квадрата. Как следует из выражения (5.1), при создании конденсаторов для увеличения емкости необходимо оптимизировать их размеры и выбирать материалы с возможно большим значением относительной диэлектрической проницаемости. Температурный коэффициент емкости αC отражает изменение емкости, обусловленное изменением температуры, и, следовательно, характеризует температурную стабильность емкости конденсатора. Общее определение этого параметра соответствует выражению:  (5.2)Дифференцируя выражения (5.1) по переменной Т, где Т – температура; S = l2, получим: 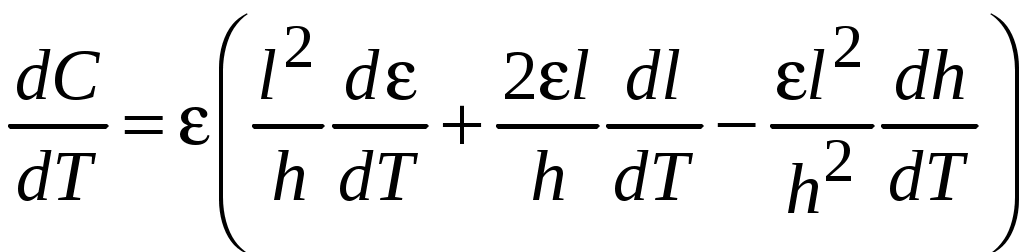 (5.3)Разделив левую и правую части выражения (5.3) на левую и правую части выражения (5.1), придем к выражению:  или αC = αε + 2αlм – αlд, где αε, αlм и αlд – температурные коэффициенты относительной диэлектрической проницаемости диэлектрика, линейного расширения металла электродов и линейного расширения диэлектрика соответственно. В металлизированных твердотельных конденсаторах, где в качестве электродов используется тонкий слой металла, нанесенный непосредственно на твердый диэлектрик, в этом случае изменение размеров электродов будет определяться линейным расширением диэлектрика, а не металла. И тогда можно считать αlм = αlд, а температурный коэффициент емкости определится выражением: αС = αε + αlд . (5.4) Характер температурной зависимости емкости конденсатора определяется механизмами поляризации рабочего диэлектрика, а параметр αC может быть положительным, отрицательным и близким к нулю. Для повышения температурной стабильности емкости конденсатора желательно, чтобы материал, применяемый для его изготовления, имел бы возможно меньшее значение температурного коэффициента относительной диэлектрической проницаемости αε. Различают высокочастотные и низкочастотные конденсаторные материалы. В качестве высокочастотных применяются неполярные полимеры, ионные диэлектрики с плотной упаковкой ионов. К низкочастотным материалам относятся полярные полимеры, диэлектрики с сегнетоэлектрическими свойствами. В области низких частот в них преобладают замедленные механизмы поляризации; потери энергии носят релаксационный характер. Материалы этой группы характеризуются повышенными значениями tg δ, но обладают весьма высокой диэлектрической проницаемостью, что позволяет изготавливать на их основе конденсаторы большой емкости с малыми габаритами. В настоящей работе исследуются параметры конденсаторов, в которых в качестве рабочего диэлектрика используются диэлектрические материалы с различными видами поляризации и механизмами диэлектрических потерь. 5.2. Описание установки Испытательная установка состоит из пульта и цифрового прибора, измеряющего емкость и tg δ. В испытательном модуле находится термостат, температура в котором может изменяться регулятором «Установка температуры». Температура в термостате измеряется с помощью термопары, подключенной к расположенному на пульте прибору, проградуированному в градусах Цельсия. В термостате размещены конденсаторы С1...C5, рабочими диэлектриками в которых являются исследуемые материалы (их наименования указаны на пульте). Выводы от расположенных в термостате конденсаторов выведены к переключателю на лицевой панели испытательного модуля, с помощью которого исследуемые конденсаторы поочередно могут быть подключены к цифровому прибору, предназначенному для измерения емкости и tg δ (измеритель иммитанса). 5.3. Проведение испытаний 5.3.1. Подготовка к испытанию Включить прибор для измерения емкости и tg δ, подготовить его к работе в соответствии инструкцией по эксплуатации, представленной на стенде.. Измерить и записать емкость С0 проводников, соединяющих образцы в термостате с измерительным прибором. 5.3.2. Измерение емкости и tg δ образцов при комнатной температуре Установить регулятор «Установка температуры» в крайнее левое положение. Включить на пульте тумблер «Сеть» и измерить значение комнатной температуры по встроенному прибору. Переключатель образцов на пульте последовательно устанавливать в положения, соответствующие определенному материалу, и произвести измерения емкости и tg δ для всех образцов при комнатной температуре. Емкость образца будет равна разности показаний прибора и С0. Результаты измерений занести в табл. 5.1. Таблица 5.1
5.3.3. Исследование температурных зависимостей емкости и tg δ Включить на пульте тумблер «Нагрев». Через 2 – 3 минуты после прекращения роста температуры отметить значение установившейся температуры и произвести измерения емкости и tg δ для всех образцов. Результаты измерений занести в табл. 5.1. Поочередно переключая регулятор «Установка температуры» в следующие положения вплоть до крайнего правого, ступенчато увеличивать температуру в термостате. При каждой вновь установившейся температуре измерять емкости и tg δ для всех образцов. После окончания измерений вернуть регулятор температуры в крайнее левое положение, выключить измеритель емкости и тумблеры «Нагрев» и «Сеть». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
