Тесты для итогового контроля по направлению 38. 03. 01 Экономика Профиль Бухгалтерский учет, анализ и аудит Тема Бухгалтерский учет в системе управления организацией ок3, 7 опк2, 3, 4 пк1,2,3,5,8,9,11,12
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
|
Тема 2: Основные понятия теории вероятностей и статистики, применяемые в эконометрике Компетенции: 1.ОПК-1 2.ОПК-2 3.ОПК-3 4. ПК-4 5. ПК-5 Тест 1 (уровень сложности 1) Статистическими называются выводы, полученные путем а) обобщения свойств выборки на генеральную совокупность б) измерения генеральной совокупности в) сбора статистических данных Тест 2 (уровень сложности 1) Выборочное среднее квадратическое отклонение является а)оценкой разброса в генеральной совокупности б)оценкой среднего в генеральной совокупности в)наиболее часто встречающейся величиной в генеральной совокупности Тест 3 (уровень сложности 1) Если линейный коэффициент корреляции между двумя случайными величинами больше нуля, то значит а)случайные величины имеют прямую линейную зависимость б)случайные величины имеют обратную линейную зависимость в)случайные величины не зависимы Тест 4 (уровень сложности 2) Вероятность события А изменяется в пределах а) 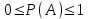 б) 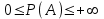 в) 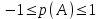 Тест 5 (уровень сложности 1) Случайной величина а) заранее не известное численное значение, зависящее от случайных обстоятельств б)количественная мера для сравнения событий по степени возможности их появления в)исход или совокупность исходов вероятностного эксперимента Тест 6 (уровень сложности 1) Законом распределения дискретной случайной величины называется а) соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями б) функция, определяющая вероятность того, что случайная величина X примет значение, меньшее, чем Х в) функция, производная от функции распределения дискретной случайной величины Тест 7 (уровень сложности 2) Функцией распределения случайной величины Х называется а)функция, определяющая вероятность того, что случайная величина X примет значение, меньшее, чем Х б)соответствие между всеми возможными значениями случайной величины и их вероятностями в)функция, производная от функции распределения непрерывной случайной величины Тест 8 (уровень сложности 2) Плотностью распределения вероятностей случайной величины Х называется а)функция, производная от функции распределения случайной величины б)соответствие между всеми возможными значениями случайной величины и их вероятностями в)функция, определяющая вероятность того, что случайная величина X примет значение, меньшее, чем Х Тест 9 (уровень сложности 2) Стандартизированное нормальное распределение имеет параметры а) 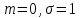 б) 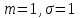 в) 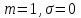 Тест 10 (уровень сложности 2) Оценка * значения параметра модели является несмещенной, если а) 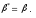 б) * обладает наименьшей дисперсией по сравнению с другими оценками в)При N, вероятность отклонения * от значения cтремится к 0 г) 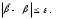 д)Математическое ожидание * равно Тест 11 (уровень сложности 2) Оценка * значения параметра модели является эффективной, если а)Математическое ожидание * равно б) * обладает наименьшей дисперсией по сравнению с другими оценками в) 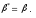 г)При N, вероятность отклонения * от значения cтремится к 0 д) 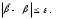 Тест 12 (уровень сложности 2) Оценка * значения параметра модели является состоятельной, если а) * обладает наименьшей дисперсией по сравнению с другими оценками б)Математическое ожидание * равно в) 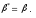 г)При N, вероятность отклонения * от значения cтремится к 0 д) 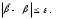 Тест 13 (уровень сложности 3) При проверке гипотезы 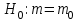 против альтернативной против альтернативной 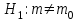 обследуется выборка обследуется выборка 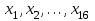 . Дисперсия неизвестна. В этом случае на уровне 0,05 критическое значение статистики равно . Дисперсия неизвестна. В этом случае на уровне 0,05 критическое значение статистики равноа) 2,1315 б)1,7531 в)1,96 г)1,645 д)-1,96 е)-1,645 Тест 14 (уровень сложности 3) Тест 14 (уровень сложности 3) При проверке гипотезы 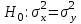 против альтернативной против альтернативной 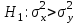 обследуются две выборки обследуются две выборки 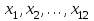 и и 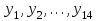 , причем было получено , причем было получено 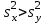 . Тогда на уровне 0,05 критическое значение статистики равно . Тогда на уровне 0,05 критическое значение статистики равноа)2,63 б)2,77 в)2,53 г)2,46 Тема 3. Линейная модель парной регрессии и методы ее оценивания Компетенции: ПК-6 ПК-7 ПК-8 ПК-10 Тест 1 (уровень сложности 1) Суть метода наименьших квадратов (МНК) отражена в следующем выражении а) 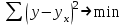 б) 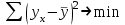 в) 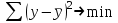 г) 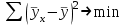 Тест 2 (уровень сложности 2) Если коэффициент уравнения регрессии (k) статистически значим, то а)k > 1 б)|k | > 1 в)k 0 г)k > 0 д)0 < k < 1 Тест 3 (уровень сложности 2) Выберите формулу для расчета коэффициента детерминации{ а) 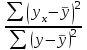 б) 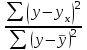 в) 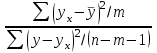 г) 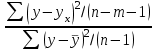 } }Тест 4 (уровень сложности 2) Выберите формулу для расчета фактического значения F – критерия Фишера а) 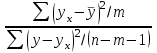 б) 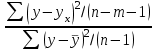 в) 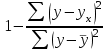 г) 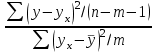 Тест 5 (уровень сложности 1) Если фактор не оказывает влияния на результат, то линия регрессии на графике{ а)параллельна оси ох б)параллельна оси оу в)является биссектрисой первой четверти декартовой системы координат Тест 6 (уровень сложности 1) Остаточная сумма квадратов равна нулю в том случае, когда а)у связан с х функционально б)значения у, рассчитанные по уравнению регрессии, равны среднему значению у в)вся общая дисперсия у обусловлена влиянием прочих факторов Тест 7 (уровень сложности 1) Общая сумма квадратов отклонений совпадает с остаточной, когда а)фактор х не оказывает влияния на результат б)прочие факторы не влияют на результат в) фактор х и прочие факторы в равной степени влияют на результат Тест 8 (уровень сложности 2) Какое из утверждений истинно а)оценки коэффициентов регрессии будут иметь нормальное распределение, если случайные отклонения распределены нормально б)чем больше стандартная ошибка регрессии (остаточная дисперсия), тем точнее оценки коэффициентов в)90%-й доверительный интервал для условного математического ожидания зависимой переменной определяет область возможных значений для 90 % -ов наблюдений за зависимой переменной при соответствующем уровне объясняющей переменной Тест 9 (уровень сложности 2) Если переменная Х принимает среднее по выборке значение х, то а)наблюдаемая величина зависимой переменной У равна среднему значению у б)регрессионная величина Ух в среднем равна среднему значению у, но не обязательно в каждом конкретном случае в)регрессионная величина Ух равна среднему значению у г)регрессионный остаток минимален среди всех других отклонений Тест 10 (уровень сложности 1) С увеличением числа наблюдений n дисперсии оценок а и b а)уменьшаются б)увеличиваются в) не изменяются Тест 11 (уровень сложности 1) С увеличением наклона прямой регрессии (b) разброс значений свободного члена а а)увеличивается б)уменьшается в)не изменяется Тема 4. Экономическая и статистическая интерпретация модели парной регрессии Компетенции: ПК-5 ПК-11 ПК-12 ПК-13 Тест 1 (уровень сложности 1) Коэффициент уравнения регрессии показывает а)на сколько % изменится результат при изменении фактора на 1% б)на сколько % изменится фактор при изменении результата на 1% в)на сколько единиц изменится результат при изменении фактора на 1 единицу г)на сколько единиц изменится фактор при изменении результата на 1 единицу д)во сколько раз изменится результат при изменении фактора на 1 единицу Тест 2 (уровень сложности 1) На основании наблюдений за 100 домохозяйствами построено эмпирическое уравнение регрессии, у- потребление, х –доход У=145,65+0,825*х Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям а)да б)нет в)частично соответствуют Тест 3 (уровень сложности 2) Для уравнения 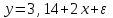 значение коэффициента корреляции составило 2. Следовательно значение коэффициента корреляции составило 2. Следовательноа) значение коэффициента корреляции рассчитано с ошибкой б) связь функциональная в) при увеличении фактора на единицу значение результата увеличивается в 2 раза г) теснота связи в 2 раза сильнее, чем для функциональной связи Тест 4 (уровень сложности 1) Зная, что регрессионная сумма квадратов составила 110,32, остаточная сумма квадратов 21,43, найдите коэффициент детерминации а)0,837 б)0,999 в)1,000 г)0,736 Тест 5 (уровень сложности 2) Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _______ процентов дисперсии обусловлено случайными факторами а)30% б)100% в)70% г)0% Тест 6 (уровень сложности 1) Подбор аналитической формы зависимости для уравнения парной регрессии возможен на основе графиков разброса…{ а)теоретических точек с координатами : 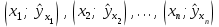 б)остатков модели 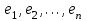 в)центрированных по факторной переменной точек с координатами 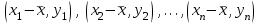 г)эмпирических точек с координатами 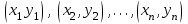 Тест 7 (уровень сложности 2) В таблице представлены результаты дисперсионного анализа. Количество наблюдений, по которым построено уравнение регрессии, можно определить как ________ плюс единица
число на пересечении столбца «df» и строки «Регрессия» а)«Остаток» + «Итого» б)число на пересечении столбца «df» и строки «Регрессия» в)сумму чисел, определенных на пересечении столбца «df» и строк «Регрессия» и «Остаток»} Тест 8 (уровень сложности 2) Эконометрическая модель представляет собой парную линейную регрессию, коэффициент корреляции факторного и результативного признака равен 0,9. Тогда коэффициент детерминации рассматриваемой модели равен… а)0,81 б)-0,9 в)0,1 г)0,99 Тест 9 (уровень сложности 3) По совокупности 15 предприятий торговли изучается зависимость между ценой 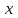 на товар А и прибылью на товар А и прибылью 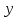 торгового предприятия. При оценке линейной регрессионной модели были получены следующие результаты торгового предприятия. При оценке линейной регрессионной модели были получены следующие результаты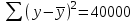 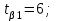 Фактическое значение F- критерия, значимость уравнения регрессии следующие а) б) в) г) Тест 10 (уровень сложности 3) Зависимость объема продаж y от расходов на рекламу х характеризуется по 12 предприятиям концерна следующим образом  t-статистика коэффициента регрессии равна а)4,7 б)3,9 в)2,4 г)2,5 Тема 5. Линейная модель множественной регрессии и оценка ее параметров Компетенции: ПК-1 ПК-4 ПК-5 ПК-6 Тест 1 (уровень сложности 1) Дано уравнение регрессии 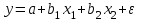 . Определите спецификацию модели . Определите спецификацию моделиа)линейное уравнение множественной регрессии б)полиномиальное уравнение парной регрессии в)линейное уравнение простой регрессии г)полиномиальное уравнение множественной регрессии Тест 2 (уровень сложности 1) В стандартизованном уравнении множественной регрессии переменными являются а)исходные переменные б)стандартизованные параметры в)средние значения исходных переменных г)стандартизованные переменные} Тест 3 (уровень сложности 1) В стандартизованном уравнении множественной регрессии 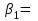 0,3; 0,3; 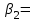 -2,1. Определите, какой из факторов -2,1. Определите, какой из факторов 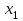 или или 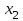 оказывает более сильное влияние на оказывает более сильное влияние на 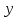 { {а) 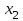 , так как l-2,1l>l0,3l , так как l-2,1l>l0,3lб)по этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии в) 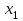 , так как 0,3>-2,1 , так как 0,3>-2,1г)по этому уравнению нельзя ответить на поставленный вопрос, так как стандартизированные коэффициенты несравнимы между собой} Тест 4 (уровень сложности 1) Добавление новой объясняющей переменной а)никогда не уменьшает значение коэффициента детерминации б)иногда уменьшает значение коэффициента детерминации в)не оказывает влияния на значение коэффициента детерминации Тест 5 (уровень сложности 1) Статистическая надежность оценки коэффициентов регрессии увеличивается а)с увеличением числа степеней свободы б)с уменьшением числа степеней свободы в)не зависит от числа степеней свободы} Тест 6 (уровень сложности 1) Скорректированный коэффициент детерминации увеличивается при добавлении новой объясняющей переменной тогда и только тогда а) когда t-статистика для этой переменной по модулю больше единицы б)когда t-статистика для этой переменной по модулю больше своего критического значения в)когда t-статистика для этой переменной по модулю больше трех Тест 7 (уровень сложности 1) Если коэффициент детерминации равен нулю, то{ а)величина зависимой переменной Y линейно не зависит от независимых переменных Xi б)величина зависимой переменной Y линейно зависит от независимых переменных Xi в)нельзя сделать вывод о линейной зависимости Y от независимых переменных Xif Тест 8 (уровень сложности 1) Укажите истинное утверждение а)скорректированный и обычный коэффициенты детерминации совпадают только в тех случаях, когда обычный коэффициент детерминации равен единице б)стандартные ошибки коэффициентов регрессии определяются значениями всех коэффициентов регрессии в)при наличии гетероскедастичности оценки коэффициентов регрессии становятся смещенными Тест 9 (уровень сложности 2) Множественный коэффициент корреляции Rух1x2=0,8. Определите, какой процент дисперсии зависимой переменной у объясняется влиянием х1 и x2 а)80% б)28% в)32% г)64% |
