УПравленческий учет в организациях АПК. ЛР1, вариант 8_Романова А.А.. Тесты на соответствие фактических распределений нормальному закону распределения в statistica руководитель Уколова А. В. (подпись, дата)
 Скачать 84.99 Kb.
|
 Институт экономики и управления АПК Кафедра статистики и эконометрики ЛАБОРАТОРНАЯ РАБОТА «Оценка однородности совокупности. Тесты на соответствие фактических распределений нормальному закону распределения в STATISTICA» Руководитель Уколова А.В. (подпись, дата) Аспирант Романова А.А. (подпись, дата) Москва, 2020 1. Оценка однородности совокупности. Тесты на соответствие фактических распределений нормальному закону распределения в STATISTICA. Вариант 8 Имеются данные о стоимости валовой продукции сельского хозяйства в расчете на 100 га сельскохозяйственных угодий (тыс. руб.) по сельскохозяйственным организациям одного из регионов РФ, представленные в EXCEL. Построим и проанализируем гистограмму распределения сельскохозяйственных организаций по этому признаку, проверим гипотезу о соответствии фактического распределения нормальному, рассчитаем описательные статистики. Представим с помощью огивы Гальтона выбранные наблюдения, с целью визуального анализа наличия особо выделяющихся наблюдений (рисунок 1). 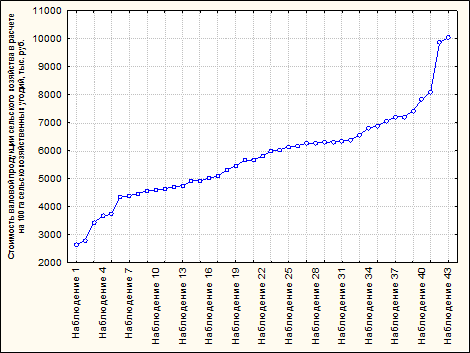 Рисунок 1 – Огива Гальтона Рассчитаем число интервалов для построения гистограммы: √43 ≈ 6 и представим гистограмму на рисунке 2. 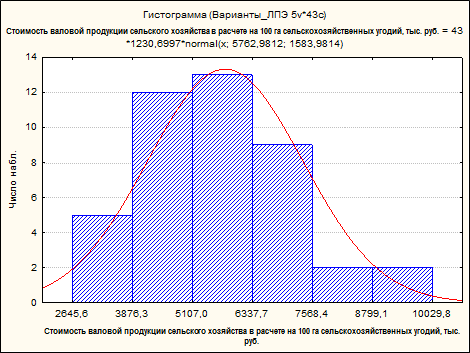 Рисунок 2 – Гистограмма интервального ряда распределения Проверка гипотезы о соответствии фактического распределения нормальному на 5% уровне значимости. Н0: фактическое распределение соответствует нормальному; На: фактическое распределение не соответствует нормальному. В таблице 1 представим фактические и ожидаемые частоты. Таблица 1 – Фактические и ожидаемые частоты
Критерий D Колмогорова-Смирнова: D0,05 = 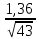 = 0,209853, т.е. Dфакт (0,120051281) не превышает D0,05 (0,209853), принимается нулевая гипотеза, т.е. распределение соответствует нормальному.Проведем тест на соответствия распределения нормальному и представим результаты графически на рисунке 3. Фактическое значение критерия-χ2 равно 1,10016, его фактическая значимость p=0,57690 больше теоретической (0,05), т.е. принимается нулевая гипотеза о соответствии фактического распределения нормальному. Критерий- χ2 дал такой же результат, как и критерий Колмогорова-Смирнова. 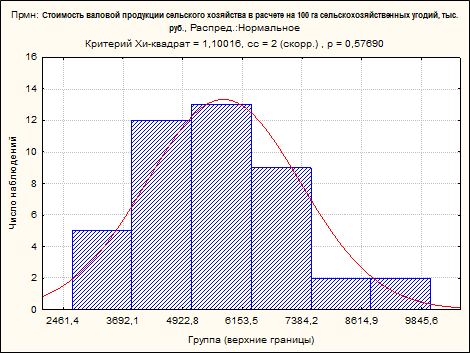 Рисунок 3 – Результаты теста χ2 Среднее значение и медиана отличаются незначительно, показатель асимметрии несколько больше 0, что говорит о небольшой правосторонней скошенности (для нормального распределения коэффициент асимметрии равен 0, положительная величина свидетельствует о правосторонней скошенности – растянутый правый рукав, отрицательная – о левосторонней скошенности), отрицательная величина коэффициента эксцесса свидетельствует о плосковершинном распределении, но отличие от нормального распределения тоже выглядит несущественным: для нормального распределения коэффициент эксцесса равен 0, положительная величина говорит об островершинном распределении, отрицательная – о плосковершинном (таблица 2). Таблица 2 – Описательные статистики
Коэффициент вариации, равный 51% также свидетельствует о средней интенсивности вариации и достаточной однородности совокупности (для нормального распределения равен 33%, по его величине судят об интенсивности вариации). |
