ЛЕКЦИИ Финансовая среда предпринимательства и предпр. риски. Тезисы лекций по дисциплине Финансовая среда предпринимательства и предпринимательские риски

• Название: Тезисы лекций по дисциплине Финансовая среда предпринимательства и предпринимательские риски
• Дата: 13.03.2023
• Размер: 1.82 Mb.
• Имя файла: ЛЕКЦИИ Финансовая среда предпринимательства и предпр. риски.doc
• Тип: Тезисы; #985552
• страница: 9 из 25

6.4. ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ

6.4.1. Процесс формирования инвестиционного портфеля

Рассмотрим проблему формирования инвестиционного портфеля. В инвестиционный портфель включены все личные активы (акции, облигации, паи в бизнесе, дом или квартира, пенсия, страховые полисы и т.д.) и все личные обязательства (ссуда на обучение, ссуда на приобретение автомобиля, закладная под недвижимость и пр.).

Не существует единой стратегии формирования инвестиционного портфеля, которая подходила бы абсолютно всем. Зато имеется несколько общих принципов, в частности, принцип диверсификации, которые годятся для всех людей, склонных к неприятию риска.

Формирование инвестиционного портфеля заключается в распределении инвестиции конкретным человеком. Это процесс поиска наилучшего соотношения между риском и ожидаемым уровнем доходности инвестиций с целью составления портфеля, в котором активы и обязательства сочетались бы с этой точки зрения оптимальным образом. В более узком смысле формирование портфеля трактуется только как принятие решений относительно сумм, которые следует инвестировать в акции, облигации и другие ценные бумаги. Если рассматривать формирование портфеля шире, то в него можно включить вопросы о том, что предпочтительнее - покупка жилья или его аренда; какого типа страховку покупать и сколько для этого выделить средств, а также решение о том, каким образом следует управлять своими обязательствами. Еще более расширенное толкование формирования портфеля включает рассмотрение таких вопросов, как определение суммы, которую целесообразно инвестировать в накопление человеческого капитала (например, в продолжение профессионального обучения). Общим элементом всех этих решений является поиск наилучшего соотношения между риском и ожидаемым уровнем доходности.

Эта глава посвящена исследованию концепций и методов, которые требуются для определения соотношения риск - доходи ость и для управления эффективностью портфеля. Основная идея заключается в том, что даже при наличии ряда общих правил формирования портфеля, которые подходят буквально всем людям, не существует единой модели портфеля или единой стратегии его формирования выбора, которыми могли бы пользоваться абсолютно все. Сейчас мы объясним, почему это так.

Стратегия формирования портфеля зависит от конкретных обстоятельств каждого человека (возраста, семейного положения, рода занятий, дохода, общего благосостояния и т.д.). Поэтому один человек, вкладывая деньги в некие ценные бумаги, увеличивает свой риск, а для другого покупка тех же ценных бумаг приводит к снижению риска. К тому же ценные бумаги, которые снижают рискованность вложений на начальных стадиях жизненного цикла семьи, могут дать совершенно противоположный эффект на поздних.

Для молодой четы, начинающей семейную жизнь, оптималь­ным вложением является приобретение дома и получение ссуды под залог этого дома. Для супругов предпенсионного возраста оптимальным решением может стать продажа дома и вложение полученных средств в ценные бумаги, что обеспечит устойчивые и регулярные денежные поступления до конца их жизни.

Составление плана формирования наилучшего портфеля начинается с определения целей инвестора и горизонтов прогнозирования. Период, или горизонт планирования - это весь промежуток времени, на который составляются планы инвестора.

Самый протяженный горизонт прогнозирования обычно охватывает период до выхода на пенсию и обычно сопоставим с индивидуальной продолжительностью жизни. Значит, у молодого человека 25 лет, рассчитывающего прожить до 65 лет, горизонт планирования равен 40 годам.

Период, или горизонт пересмотра решения - это промежуток времени между двумя решениями, касающимися формирования инвестиционного портфеля. Продолжительность периода пересмотра решении устанавливается каждым человеком индивидуально.

Некоторые инвесторы производят пересмотр своих портфелей через определенные интервалы, например раз в месяц (при оплате счетов) или раз в год (при заполнении налоговой декларации). Инвесторы со средним достатком, у которых основная часть сбережений находится на банковских счетах, пересматривают свои инвестиционные портфели довольно редко и нерегулярно, обычно в связи с такими не часто случающимися событиями, как женитьба или развод, появление ребенка или получение наследства. Причиной для пересмотра инвестиционного портфеля могут стать также резкие колебания цен на те или иные активы, которыми владеет данный индивидуум.

Инвесторы, вложившие значительные суммы в акции и облигации, могут пересматривать свой портфель ежедневно, а иногда и чаще. У них самым коротким периодом пересмотра решения является период биржевых торгов; именно он определяет минимальный промежуток времени, через который инвестор пересматривает свой портфель.

Индивидуум не может контролировать протяженность периода биржевых торгов. Период биржевых торгов может равняться неделе, дню, часу или даже минуте - в зависимости от структуры рынка в данной экономической системе (например, от того, в какое время открыты биржи ценных бумаг, и от того, существуют ли организованные внебиржевые рынки).

В условиях сегодняшней глобализации финансовой среды покупка и продажа большинства ценных бумаг может быть осуществлена в любой точке земного шара в любое время дня и ночи. Следовательно, для таких ценных бумаг горизонт биржевых торгов очень короток.

Сегодняшние решения о составе инвестиционного портфеля основываются на предположениях о том, что может произойти завтра. План, при разработке которого сегодняшние решения принимаются с учетом ваших последующих действий, называется стратегией.

При формулировании стратегии инвестирования крайне важным фактором является частота, с которой инвестор пересматривает свой портфель, покупая или продавая ценные бумаги. Например, инвестор выбирает стратегию инвестирования «избыточного» капитала в акции. «Избыточным» в данном случае является капитал, превышающий некий предел, необходимый ему для поддержания определенного уровня жизни. Если курс этих акций со временем пойдет вверх, то инвестор увеличит долю портфеля, отведенную на вложения в эти акции. Однако, если акции станут дешеветь, инвестор уменьшит долю вложенных в них капиталов. Если курс акций снизится до такого предела, что привычный стандарт жизни окажется под угрозой, инвестор вообще избавится от этих акций,

Целью исследования количественного соотношения между риском и ожидаемым уровнем доходности является формирование портфеля, инвестиции в который обеспечивали бы инвестору максимальную ожидаемую ставку доходности при той степени риска, на которую он согласен. В процессе анализа мы будем говорить о рискованных активах, не подразделяя их на облигации, акции, опционы, страховые полисы и пр., потому что, как уже говорилось выше в этой главе, степень рискованности каждого отдельного актива зависит в первую очередь от конкретных обстоятельств жизни данного инвестора.

Оптимизация портфеля обычно состоит из двух этапов:

1. 
   выбора оптимальной комбинации рискованных активов и
   
2. 
   объединения полученного оптимального набора рискованных активов с безрисковыми активами. В целях упрощения процесса мы начнем со второго этапа - объединения портфеля, содержащего рискованные активы, с безрисковыми активами. Этот единственный рискованный портфель составлен из множества рискованных активов, скомбинированных оптимальным образом.
   

6.4.2. Портфель из совокупности безрискового актива с рискованным активом

В теории формирования наилучшего портфеля безрисковым активом считается ценная бумага, которая предлагает полностью предсказуемую ставку доходности в расчетных денежных единицах, выбранных для анализа, и в пределах периода пересмотра решения данного инвестора. Если брать более общую ситуацию, когда нет конкретного инвестора, то безрисковыми активами следует считать те из них, которые предлагают инвестору предсказуемую ставку доходности в пределах периода биржевых торгов,

Предположим, что вы решили инвестировать 10000 у.е. Перед вами безрисковый актив с процентной ставкой 0,08 годовых и рискованный актив с ожидаемой ставкой доходности 0,14 годовых и стандартным отклонениям 0,02. Какую часть от 10000 у.е. вам следует вложить в рискованный актив?

Все доступные комбинации риска и доходности показаны в табл. 6.2 и на рис. 6.7.
Таблица 6,2

Ожидаемая доходность и стандартное отклонение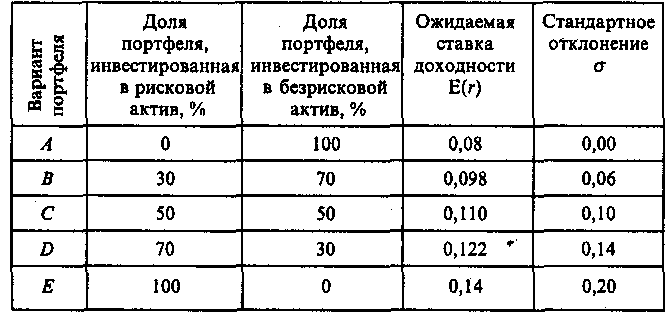



Ожидаемая ставка доходности определяется по формуле (6.2.1), а стандартное отклонение равно: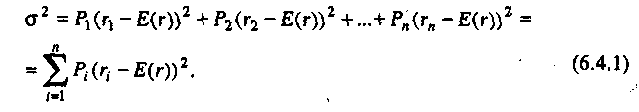



Однако, если в одном портфеле объединены рискованный и безрисковый активы, то стандартное отклонение доходности такого портфеля равно стандартному отклонению доходности рискового актива σ_p умноженному на его вес Vв портфеле. Тогда получим формулу стандартного отклонения доходности портфеля в виде

Для нашего примера σ = 0,2 • V.

На основании двух последних столбцов табл. 6.2.строим график зависимости между риском аи ожидаемой доходностью Е(r) (рис. 6.7).

Точке А на рис. 6.7 соответствует ситуация, когда вы вкладываете все свои деньги в безрисковый актив, а точке Е - ситуация, когда вы инвестируете все свои деньги в рискованный актив. Линия АЕ представляет набор (портфель) свободно доступных вам вариантов из рискованного и безрискового актива. Так портфель С наполовину состоит из рискованного актива, наполовину - из безрискового.

Если мы хотим определить состав портфеля, для которого ожидаемая ставка доходности равна 0,12, то судя по рис. 6.7 такая точка лежит между точками С и D, но чтобы точно ответить на этот вопрос нужно записать и решить более общую задачу.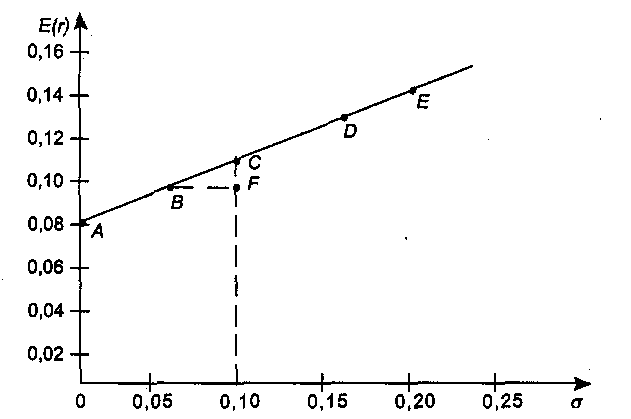


Рис. 6.7. Соотношение между риском и ожидаемой доходностью инвестиционного портфеля
Пусть Vобозначает долю от Р у.е., которая вложена в рисковой актив. Оставшаяся часть будет равна (1 - V) и она вложена в безрисковой актив. Ожидаемая ставка доходности портфеля Е(r) определится как



где Е(r_р) - обозначает ожидаемую ставку доходности рискованного актива, a r_b - безрисковая ставка доходности.

Для нашего примера:



Смысл уравнения (6.4.3) заключается в том, что базовой ставкой доходности для любого портфеля является безрисковая ставка доходности (0,08 в нашем примере). Кроме того, предполагается, что инвестиции в портфель принесут дополнительную премию за риск, которая зависит от премии за риск по рискованному активу (Е(r_р) - r_b) (0,06 в нашем случае) и от доли портфеля, инвестированной в рискованный актив и обозначенной V.

Чтобы определить состав портфеля, соответствующий ожидаемой ставке доходности в 0,12, надо подставить нужные значения в уравнение (6.4.3) и вычислить V.



Таким образом, портфель на 66,7 % должен состоять из рискованного актива, и на 33,3 % — из безрискового.

Далее определяем связь между стандартным отклонением и долей инвестиций, приходящихся на рискованный актив. В формулу (6.4.2) подставляем наши данные σ_р = 0,2 и V = 0,667 и находим стандартное отклонение доходности портфеля:



Из (6.4.2) находим V и подставляем его в выражение (6.4.3), получаем



т.е. нашли связь между ожидаемой доходностью и риском в виде прямой линии.

Для нашего примера

Угловой коэффициент этой прямой равен 0,30, а угол наклона, равный примерно 16,7°, характеризует дополнительную ожидаемую доходность, предлагаемую рынком для каждой дополнительной единицы риска, которую согласен нести инвестор.

Рассмотрим предыдущий пример, дополнительно включив в него еще один рискованный актив 2, который имеет ожидаемую ставку доходности 0,098 в год и стандартное отклонение 0,30. На рис. 6.7 это точка F.

Нужно получить эффективный портфель, под которым мы понимаем такой портфель, который предлагает инвестору максимально возможный ожидаемый уровень доходности при заданном уровне риска.

Инвестор, который хочет получить ожидаемую ставку доходности в 0,098 годовых, может добиться своей цели, вложив всю сумму в рискованный актив 2. Тогда он окажется в ситуации, описываемой точкой F.Но при этом портфель инвестора неэффективен, потому что в точке В инвестор может получить такую же ожидаемую ставку доходности (0,098 в год) при меньшем значении стандартного отклонения.

Из табл. 6.2 видно, что в точке В стандартное отклонение составляет только 0,06. Это объясняется тем, что 30 % инвестиций данного портфеля вложены в рискованный актив 1, а 70 % - в безрисковый актив. Действительно, не желающий рисковать инвестор выберет на прямой риск-доходность, соединяющей точки В и Е,любую точку - только не точку F. Любая из этих точек соответствует вполне приемлемой ситуации, когда некоторое количество рискованного актива 1 уравновешивается безрисковым активом. Например, портфель в точке С имеет стандартное отклонение, равное стандартному отклонению рискованного актива 2 (σ = 0,10), но его ожидаемая ставка доходности составляет 0,110 годовых, а не 0,098. Из табл. 6.2, нам известно, что такое соотношение соответствует портфелю, который на 50 % состоит из рискованного актива 1 и на 50 % из безрискового актива.

С помощью уравнений (6,4.3) и (6.4.2) можно определить состав других эффективных портфелей, которые описываются точками между В и С и имеют, следовательно, более высокую ожидаемую ставку доходности и меньшее значение стандартного отклонения в сравнении с рискованным активом 2. Рассмотрим, например, портфель, который на 62,5 % состоит из рискованного актива 1 и на 37,5 % - безрискового актива. Его ожидаемая ставка доходности равна 0,1175 в год, а стандартное отклонение составляет 0,125.
6.4.3. Эффективный портфель, составленный из двух рискованных активов

Пусть портфель составлен из двух видов рискованных активов, в котором V- это доля рискованного актива 1, а (1 - V) - это доля рискованного актива 2. Тогда среднее значение ставки доходности такого портфеля будет:



Формула дисперсии из (6.1.4) для двух активов запишется как



Здесь ожидаемые ставки доходности рискованных активов обозначены соответственно через Е(r₁) и E(r₂), а через ρобозначен коэффициент корреляции.

Для рискованного актива 1; среднее значение 0,14; стандартное отклонение 0,20; а для рискованного актива 2: среднее значение 0,12; стандартное отклонение 0,16. Коэффициент корреляции для обоих активов равен нулю, т.е. ρ = 0.

В зависимости от доли средств актива 1 и актива 2 по формуле (6.4.5) и (6.4.6) подсчитаны значения Е(r) и σ и записаны в двух последних столбцах табл. 6.3.

Таблица 6.3

Соотношение риск-доходность для портфелей с двумя рискованными активами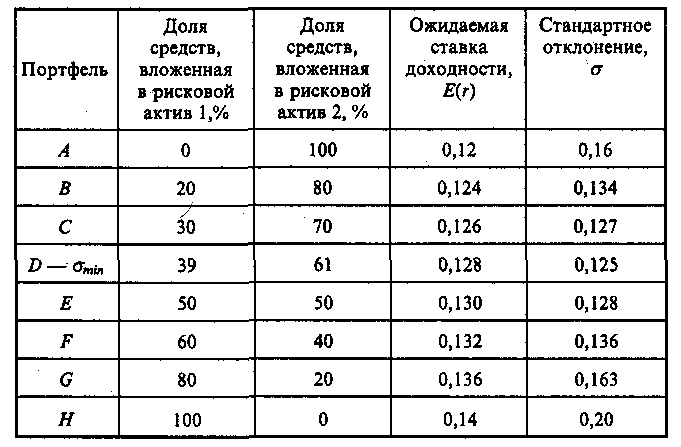



Например, для точки В



По точкам Е(r) и σ, взятым из табл. 6.3, построена кривая соотношения риск - доходность для двух рискованных активов (рис. 6.8).

Дадим анализ кривой рис. 6.8. Берем точку А и перемещаем часть наших капиталов из рискованного актива 2 в рискованный актив 1. При этом наблюдается не только повышение средней ставки доходности, но и снижение стандартного отклонения. Оно снижается до точки D, а затем вновь повышается. Найдем координаты точки D, соответствующей минимальному значению σ.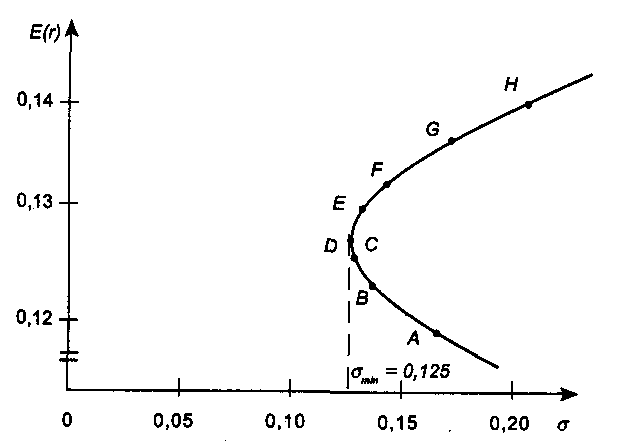



Рис. 6.8. Соотношение между риском и ожидаемой доходностью
для рисковых активов
Берем функцию (6.4.6) и считаем σ=σ(ν), а σ₁ σ₂ и ρ постоянными. Тогда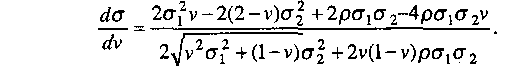



Приравнивая производную нулю, находим точку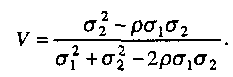



Исследования показывают, что в этой точке кривая σ=σ(ν) имеет минимум и, следовательно,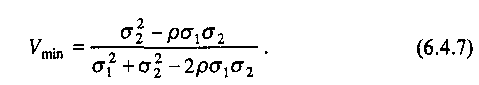



По этой формуле получаем



т.е. портфель с минимальной дисперсией состоит из 39 % активов 1 и 61 % активов 2.
6.4.4. Оптимальный портфель, составленный из безрисковых активов и рискованных активов

Теперь рассмотрим комбинации риск - доходность, которые мы можем получить посредством объединения безрискового актива с рискованными активами 1 и 2, параметры которых оста­ются прежними, а безрисковая ставка доходности r_b= 0,08.

На рис. 6.9 показано графическое представление всех возможных комбинаций риск - доходность. Кривая A_PDHесть кривая, изображенная на рис. 6.8, а прямая АН (рис. 6.9) представляет со­бой график, изображенный на рис. 6.7. Прямая показывает ряд комбинаций риск - доходность, которые могут быть получены посредством объединения безрискового актива с рискованным активом 1.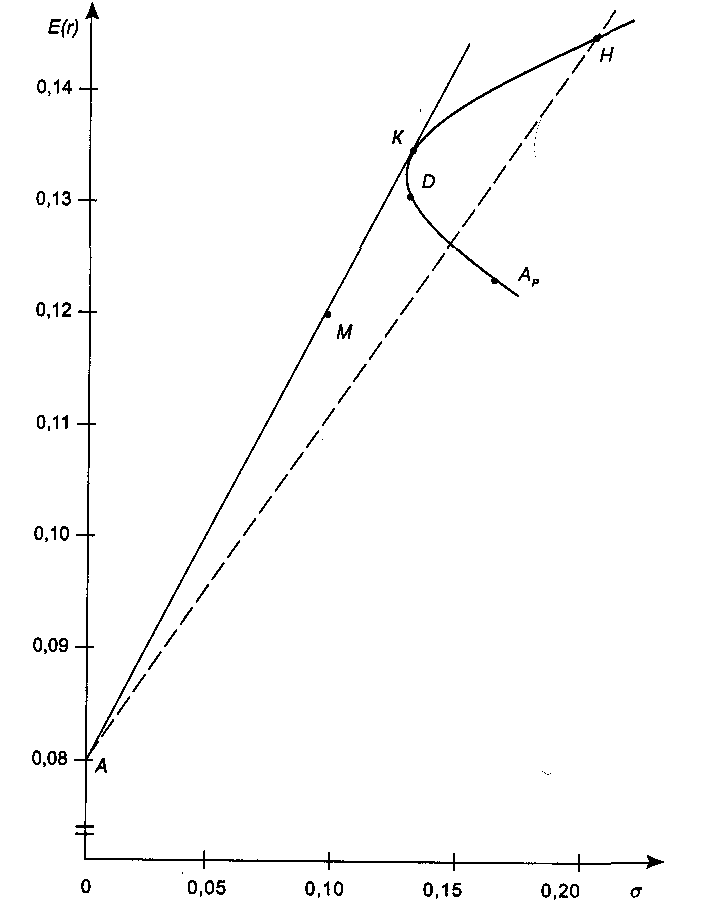



Рис. 6.9. Оптимальная комбинация рискованных активов
Прямая линия, соединяющая точку А с любой точкой кривой, соединяющей точки А_р, Dи Н,представляет собой график, описывающий соотношение риск - доходность для всех комбинаций следующих трех активов: рискованных активов 1 и 2 с безрисковыми активами. Наибольшее значение этого соотношения, которое мы можем достичь, находится на линии, соединяющей точки А и К.Точка К является общей точкой прямой линии, выходящей из точки А, и кривой и, кроме того, это точка касания прямой и кривой. Исходя из этих условий формула для определения долей портфеля в точке К имеет вид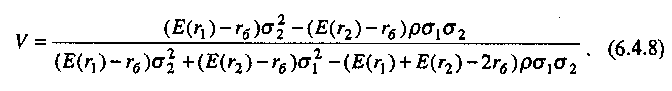



Такой рискованный портфель, который соответствует точке К на рис. 6.9, называется оптимальной комбинацией рискованных активов. Именно объединением этого портфеля рискованных активов с безрисковым активом достигается формирование максимально эффективного портфеля.

Хотя и другие рискованные эффективные портфели из модели Марковича могут быть скомбинированы с безрисковым активом, портфель К заслуживает особого внимания. Почему? Потому что не существует портфеля, состоящего из рискованных ценных бумаг, который, будучи соединен прямой линией с точкой, соответствующей безрисковому активу, лежал бы левее и выше его. Другими словами, из всех линий, которые могут быть проведены из точки, соответствующей безрисковому активу, и соединяют эту точку с рискованным активом или рискованным портфелем, ни одна не имеет больший наклон, чем линия, идущая в точку К.

Это важно потому, что часть эффективного множества модели Марковича отсекается этой линией. В частности, портфели, которые принадлежали эффективному множеству в модели Марковица и располагались между минимально рискованным портфелем и портфелем К, с введением возможности инвестирования в безрисковые активы не являются эффективными. Теперь эффективное множество состоит из прямого и искривленного отрезка. Прямой отрезок идет от безрискового актива в точку К и поэтому представляет портфели, составленные из различных комбинаций безрискового актива и портфеля К. Искривленный отрезок расположен выше и правее точки К и представляет портфели из эффективного множества модели Марковица.

Подставляя данные в формулу (6.4.8), получаем;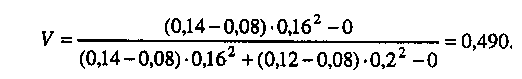



Это означает, что оптимальной комбинацией рискованных активов (для портфеля в точке касания с прямой, который еще называют тангенциальным портфелем), является 49 % рискованного актива 1 и 51 % рискованного актива 2. Ожидаемая ставка доходности и стандартное отклонение в точке К будут равны:

Тогда новый график для эффективного соотношения Е(r) = f(σ) будет иметь вид: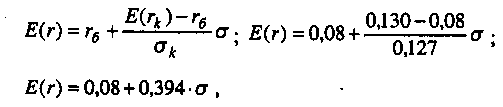



где угол наклона - отношение доходности к риску - равен 0,394. Для прежней прямой Е(r) = 0,08 + 0,30 • σ угол наклона равен 0,30. Отсюда видно, что теперь инвестор находится в лучшем положении, потому что он может достичь более высокой ожидаемой ставки доходности для любого уровня риска, на который готов идти. Теперь обобщим наши исследования относительно создания эффективного портфеля, когда имеются два вида рискованных активов и один безрисковой актив. Напомним, что предпочтения при формировании портфеля зависят от стадии жизненного цикла, на которой находится инвестор, периода (горизонта) планированности и отношения к риску. Следовательно, инвестор может выбрать позицию в любой точке на отрезке АК (рис. 6.9). На этом отрезке выбираем точку М,портфель, соответствующий этой точке, на 50 % состоит из портфельных инвестиций в общей точке К (тангенциальный портфель) и на 50 % из инвестиций в безрисковый актив.

Преобразуем уравнение (6.4.3) и (6.4.2) таким образом, чтобы они отражали тот факт, что портфель в точке касания К является теперь единственным рискованным активом, который следует объединить с безрисковым активом. Находим



Учитывая, что тангенциальный портфель состоит на 49 % из рискованного актива 1 и на 51 % - из рискованного актива 2, и на долю рискованных активов приходится 50 % всего портфеля, определяем, что в портфеле будет 0,5 • 49 % = 24,5 % рискованных активов 2. Таким образом, состав портфеля М будет следующим: доля безрискового актива составляет 50 %, доля рискованного актива 1 - 24,5 % и доля рискованного актива 2 - 25,5 %.

Следовательно, если вы инвестировали 10000 у.е. в портфель М, то 5000 у.е. инвестировано в безрисковый актив, 2450 у.е. - в рискованный актив 1 и 2550 у.е. - в рискованный актив 2.

Таким образом, существует только один портфель с рискованными активами, который оптимальным образом можно объединить с безрисковым активом. Этот портфель мы назовем оптимальной комбинацией рискованных активов, соответствующий общей (касательной) точке К. Следовательно, предпочтительный портфель всегда является комбинацией портфеля рискованных активов в общей точке и безрискового актива.

Важно отметить, что при поиске оптимальной комбинации рискованных активов нам не нужно ничего знать ни о благосостоянии инвестора, ни о его предпочтениях. Состав этого портфеля зависит только от ожидаемых ставок доходности и стандартных отклонений рискованного актива 1 и рискованного актива 2 и от корреляции между ними. Это означает, что все инвесторы, которые согласились на такие характеристики доходности (среднее значение, стандартное отклонение, корреляция), захотят инвестировать в один и тот же тангенциальный портфель, дополненный безрисковым активом. Вот общее правило, применимое ко всем случаям, когда имеется множество рискованных активов. Всегда существует оптимальный портфель рискованных активов, который все инвесторы, избегающие риска и имеющие одинаковые представления о характеристиках доходности, будут объединять с безрисковым активом с целью получения наиболее предпочтительного портфеля.
6.4.5. Портфели с множеством рискованных активов

При наличии большого числа рискованных активов мы используем двухэтапный метод создания портфеля, аналогичный тому, который был рассмотрен в предыдущем разделе. На первом этапе мы рассматриваем портфели, состоящие только из рискованных активов, а на втором этапе мы определяем тангенциальный портфель рискованных активов, который можно объединить с безрисковым активом. Такая работа требует большого количества вычислений, поэтому лучше выполнять ее на компьютере.

На рис. 6.10 показаны исходные данные и результат их обработки в программе электронных таблиц, используемой для оптимизации портфеля. Индивидуальные базовые активы - это рискованный актив 1, рискованный актив 2 и т.д. Они представлены затененными точками на диаграмме слева. Кривая, лежащая выше и правее этих точек, называется границей эффективного множества портфелей рискованных активов. Она определяется как множество портфелей с рискованными активами, каждый из которых предлагает инвесторам максимально возможные ставки доходности при любом заданном стандартном отклонении.

Error: Reference source not found

Рис. 6.10. Программа электронных таблиц для оптимизации портфеля
Отдельные базовые активы находятся с внутренней стороны границы эффективности по той причине, что обычно существует некая комбинация из двух и более базовых активов, ожидаемая ставка доходности которой при таком же стандартном отклонении выше, чем у этих базовых активов.

Оптимальное сочетание рискованных активов обнаруживается в общей точке пересечения прямой, которая начинается в точке, представляющей безрисковый актив (на вертикальной оси), и границы эффективности рискованных активов. Отрезок, соединяющий точку безрискового актива и тангенциальную точку, которая соответствует оптимальной комбинации рискованных активов, представляет самые лучшие соотношения риск - доходность.

Теперь вернемся к вопросу, который мы уже затрагивали ранее. Каким образом финансовый посредник (например, компания, предлагающая инвесторам инвестиции в управляемые ею взаимные фонды) составляет «финансовое меню» из разных комбинаций активов, чтобы предложить его своим клиентам? Мы только что показали, что нахождение оптимальных комбинаций рискованных активов зависит только от ожидаемого уровня доходности, стандартных отклонений базовых рискованных активов и от корреля­ции между ними. Оно не зависит от предпочтений инвесторов. Следовательно, для того, чтобы создать эффективный портфель, сведения о предпочтениях инвесторов совершенно не нужны.

Итак, клиенты возлагают на финансовых посредников, которые специализируются на соответствующих видах деятельности, составление прогноза ожидаемого уровня доходности активов, стандартных отклонений и корреляции; посредники берут на себя также функцию комбинирования базовых активов в оптимальных пропорциях. Следовательно, клиентам остается только выбрать размеры капиталов, которые они намерены вложить в оптимальный рискованный портфель.

Статистическая модель выбора активов для инвестиционного портфеля, опирающаяся на среднее значение доходности и ее дисперсию, заложила теоретические основы финансового посредничества взаимных фондов. Начиная с конца 60-х годов академические исследования в области составления оптимального портфеля вышли за пределы этой модели и занялись динамическими версиями. В них межвременная оптимизация решений инвесторов относительно сбережения - потребления, принимаемых на опре­деленных стадиях жизненного цикла домохозяйства, объединяется с распределением высвободившихся сбережений среди альтернативных направлений инвестиций. В этих моделях спрос на индивидуальные активы зависит от более серьезных факторов, нежели достижение оптимальной диверсификации, как было показано выше. Он является также следствием желания хеджировать различные риски, не включенные в первоначальную модель. В число рисков, которые создают потребность в хеджировании при принятии решений о составе портфеля, входят риск смерти, риск случайных изменений процентных ставок и ряд других. Динамические модели значительно обогатили теоретические воззрения на роль ценных бумаг и финансовых посредников при формировании инвестиционного портфеля.

В практике управления активами в рамках инвестиционного менеджмента по-прежнему преобладает базовый метод оценки риска на основании вычисления средней доходности и дисперсии портфеля (mean-varianceapproach). Однако все меняется. Благодаря более совершенным моделям составления портфеля инвестиционные компании теперь могут предлагать клиентам не просто оптимальные комбинации рискованных и безрисковых активов, а целое «семейство» взаимных фондов. Эти дополнительные фонды позволяют создавать оптимальные хеджинговые портфели, рассчитанные на еще более полное удовлетворение запросов самых разных клиентов. Инвестиционная компания может создавать из своих взаимных фондов интегрированные продукты, объединяя разные комбинации своих фондов в пропорциях, которые соответствуют запросам клиентов на разных стадиях их жизненных циклов.
6.5. МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ АКТИВОВ КАПИТАЛА

6.5.1. Основы ценовой модели рынка капитала

Ценовая модель рынка капитала (capitalassetpricingmodel, САРМ) представляет собой равновесную теорию, основанную на приведенных в п. 6.4. принципах формирования инвестиционного портфеля, ЦМРК была разработана в начале 60-х годов. Толчком для ее создания послужили поиски ответа на следующий вопрос: какими должны были бы быть премии за риск, на которые согласны инвесторы в ситуации рыночного равновесия, если бы все они руководствовались одними и теми же прогнозами относительно ожидаемых ставок доходностей и рисков инвестиций в ценные бумаги, делая при этом оптимальный выбор для своих портфелей ценных бумаг в соответствии с принципами эффективной диверсификации?

Основополагающая посылка ЦМРК состоит в том, что в состоянии равновесия доход от сделок на финансовом рынке вознаграждает людей за их рискованные инвестиции. Обычно люди не склонны к рискованным действиям, в связи с чем премия за риск для всей совокупности рискованных активов должна быть реально ощутимой, чтобы у людей присутствовало желание владеть рискованными активами, существующими в экономике.

Однако рынок не вознаграждает людей, которые владеют неэффективными портфелями ценных бумаг - т.е. подвергают себя воздействию рисков, которые могут быть устранены при оптимальном подходе к диверсификации рисков. Таким образом, премия за риск любой отдельной ценной бумаги не связана с ее «индивидуальным риском». Ее величина скорее обусловлена вкладом данной ценной бумаги в общий риск всего эффективно диверсифицированного портфеля.

В п. 6.4 показано, что каждый .эффективный портфель ценных бумаг может быть создан посредством объединения в нем двух конкретных типов активов: безрисковых активов и оптимальным образом скомбинированных рискованных активов. Последний тип портфеля называют еще тангенциальным, имея в виду, что параметры риска и доходности рискованных активов, которые в него входят, соответствуют точке касания луча, проведенного из точки на оси Е(r),относящейся к безрисковому активу А, к границе эффективности. Теоретическое обоснование ЦМРК опирается на два предположения.

Предположение 1. Инвесторы имеют одинаковые представления в отношении прогнозов по ожидаемым ставкам доходности, показателям стандартных отклонений доходности (т.е. риску) и корреляции между рискованными ценными бумагами. Следовательно, они вкладывают свои средства в рискованные активы таким образом, что в итоге сосредотачивают их в своих портфелях в одних и тех же пропорциях.

Предположение 2. Инвесторам присуще оптимальное поведение. Поэтому на находящемся в равновесии рынке курс ценных бумаг устанавливается таким образом, что если инвесторы владеют оптимальными портфелями ценных бумаг, то совокупный спрос на ту или иную ценную бумагу равняется ее совокупному предложению.

Исходя из этих двух посылок и с учетом того, что относительное количество рискованных активов у каждого инвестора оказывается одинаковым, мы приходим к выводу, что фондовый рынок может находиться в состоянии равновесия только в том случае, если эти оптимальные пропорции владения ценными бумагами соответствуют пропорциям, в которых активы представлены на рынке. Портфель, состоящий из всех имеющихся ценных бумаг, пропорции инвестирования в которые соответствуют их доли в общей капитализации рынка, называется рыночным портфелем. Состав рыночного портфеля отражает предложение существующих финансовых активов, оцененных по текущим рыночным ценам.

Рассмотрим более детально, что же подразумевается под рыночным портфелем. В рыночном портфеле доля, приходящаяся на ценную бумагу i, равна отношению рыночной стоимости эмитированной i-й ценной бумаги к рыночной стоимости всех выпущенных в обращение ценных бумаг. Для простоты рассмотрения предположим, что существуют только три вида ценных бумаг: акции А,акции В и безрисковые ценные бумаги. Общая рыночная стоимость каждого из финансовых активов составляет: 5 млн у.е. для акций А,3 млн у.е. для акций В и 2 млн у.е. для безрисковых ценных бумаг. Общая рыночная стоимость для всех этих активов равна 10 млн у.е. Таким образом, рыночный пакет состоит из 50 % акций А,30 % акций В и 20 % безрисковых ценных бумаг.

Как следует из ЦМРК, в условиях рыночного равновесия рискованные активы в портфеле каждого из инвесторов будут находиться в той же пропорции, что имеет место для всего рыночного портфеля. В зависимости от своей меры неприятия риска инвесторы обладают различными наборами безрисковых и рискованных активов, однако процентное соотношение рискованных ценных бумаг в портфелях инвесторов оказывается для всех них одинаковым. Для данного примера можно сказать, что рискованная часть портфеля ценных бумаг каждого инвестора будет состоять из 50 % акций А и 30 % акций В.

Рассмотрим двух инвесторов, каждый из которых собирается сделать вложения размером в 10000 у.е. У первого инвестора восприятие риска равняется среднему значению для всех инвесторов, и, следовательно, он владеет каждым активом в соответствии с тремя пропорциями, которые присущи рыночному портфелю, Таким образом, 5000 у.е. вложены в акции А, 3000 в акции В,а 2000 - в свободные от риска ценные бумаги. Второй инвестор проявляет большее по сравнению со средним неприятие риска и предпочитает в связи с этим вложить 4000 у.е. в безрисковые ценные бумаги и 6000 у.е. - в рискованные ценные бумаги. Вложение второго инвестора а акции А составит 0,5 х 6000 у.е., или 3000 у.е., а его вложение в акции В окажется равным 0,3 х 6000 у.е., или 1800 у.е. Таким образом, оба инвестора будут владеть акциями А и В впропорции 50 : 30 = (5000 + 3000): (3000 + 1800).

Этот основной тезис ЦМРК иллюстрируется также рис. 6.11, где изображен график соотношения Е(у), скоторым сталкивается каждый из инвесторов, определяя направления своих инвестиций. Поскольку тангенциальный портфель, или, говоря иначе, оптимальная комбинация рискованных активов, соответствует такому же, как и для рыночного портфеля, относительному содержанию рискованных активов, то рыночный портфель расположен на любой из точек графика Е(σ). В ЦМРК график риск - доходность называется графиком рынка капиталов, или ГРК. Точка Е на рис. 6.11 показывает соотношение риск – доходность для рыночного портфеля, точка А соответствует безрисковым активам, а ГРК представляет собой прямую линию, соединяющие эти две точки.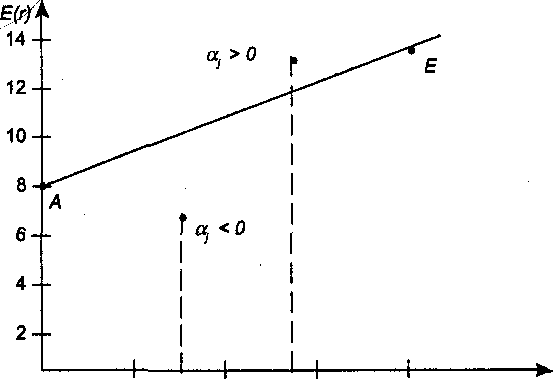



Рис. 6.11. График рынка капиталов
В соответствии с ЦМРК график рынка капиталов в условиях рыночного равновесия представляет лучшие из возможных для инвесторов комбинации «риск - доходность». Несмотря на то, что все инвесторы будут стремиться к достижению точек, лежащих на ГРК, конкуренция на рынке будет действовать в сторону понижения курса акций, в результате чего выбор инвесторов будет характеризоваться точками, принадлежащими графику рынка капиталов.

Исходя из формулы (6.4.4) график рынка капиталов описывается формулой:



где E(r) – ожидаемая доходность эффективного портфеля;

σ_n– стандартное отклонение (риск) рыночного портфеля;

E(r_n) – ожидаемая доходность рыночного портфеля;

r_b– доходность безрисковых ценных бумаг;

σ – стандартное отклонение (риск) эффективного портфеля.

Таким образом, наклон ГРК равен частному от деления премии за риск рыночного портфеля на величину его риска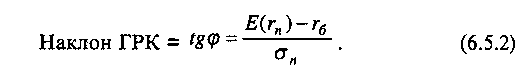



Проведем экономическую интерпретацию этой величины. Числитель характеризует превышение доходности рыночного портфеля над безрисковой ставкой. Это премия за риск инвестирования в рисковый рыночный портфель, а не в безрисковый актив. Знаменатель - риск рыночного портфеля. Таким образом, наклон дает величину премии на «единицу рыночного риска». Поскольку эффективная линия рынка определяет максимальную достижимую доходность, компенсирующую выбранный уровень риска, то все ее точки соответствуют «взаимно сбалансированным» решениям инвесторов, т.е. она отображает равновесное со­стояние рынка. Наклон линии рынка определяет требуемую дополнительную доходность на каждую «единичную» порцию рынка. Поэтому наклон эффективной линии рынка называют равновесной рыночной ценой риска.

Согласно уравнению эффективной линии рынка, доходность портфеля - это сумма безрисковой ставки и премии за риск (по портфелю), которая представляет собой произведение рыночной цены риска (т.е. наклона линии риска) и риска портфеля:

Е(r) = Безрисковая ставка + Цена риска Ч Риск портфеля.

Из ЦМРК следует, что для большинства инвесторов результаты их пассивной стратегии, предусматривающей комбинирование безрисковых активов с вложениями в акции инвестиционных фондов, придерживающихся стратегии индексирования при операциях с рискованными ценными бумагами, так же хороши, как если бы они вели активный поиск доходных ценных бумаг и пытались «победить» рынок. Самые усердные и знающие свое дело инвесторы действительно получают вознаграждение за свои усилия, однако с течением времени конкуренция между ними сводит их доходы к минимуму, необходимому для того, чтобы они просто продолжали свою работу. Все остальные могут при этом извлечь выгоду из прилагаемых ими усилий за счет следования собственной стратегии пассивного инвестирования.

Еще одно следствие, вытекающее из концепции ЦМРК, состоит в том, что Премия за риск для каждой отдельной ценной бумаги пропорциональна только ее вкладу в совокупный риск всего рыночного портфеля. Премия за риск не зависит от риска, присущего ей в отдельности. Таким образом, в соответствии с ЦМРК, в условиях равновесия инвесторы получают вознаграждение, соответствующее более высокой ожидаемой ставке доходности, только при принятии на себя всего рыночного риска. Это неустранимый, или необходимый риск, который они должны принять для получения ожидаемой доходности.

Логика рассуждений состоит в том, что, поскольку все эффективные комбинации «риск - доходность» могут достигаться за счет простого объединения рыночного портфеля и безрисковых активов, единственный риск, которому вынужден подвергаться инвестор для получения эффективного портфеля ценных бумаг, - это рыночный риск, т.е. риск всего рыночного портфеля в целом. Таким образом, рынок не вознаграждает инвесторов за принятие на себя любых нерыночных рисков, т.е. за инвестиции в активы, выходящие за пределы рыночного портфеля. Рынок не вознаграждает инвесторов за выбор неэффективных портфелей ценных бумаг.

Иногда это следствие применения ЦМРК подчеркивают утверждением о том, что для ценной бумаги «имеет значение» только такой риск, который обусловлен рынком.