ЛЕКЦИИ Финансовая среда предпринимательства и предпр. риски. Тезисы лекций по дисциплине Финансовая среда предпринимательства и предпринимательские риски
 Скачать 1.82 Mb. Скачать 1.82 Mb.
|
Sкв=3,6/4/2=0,45 млн.руб.Пример 5.8. Вексель был учтен за 15 дней до срока погашения по ставке 18% годовых. В результате учета владелец векселя получил 9,925 млн. рублей. Определить номинальную стоимость векселя. Решение. Дисконт dT=9.925*15/(360*100/18-15)=0,075 млн. рублей. dТ=S(T)pT/(100*360); S(T)=S(0) + dT=9,925 + 0,075 = 10.0 млн. руб. Пример 5.9. Банк предоставил клиенту кредит на три месяца с 15.03.03г. по 15.06.03г. под залог 200 акций, курсовая стоимость которых в день выдачи кредита (15.03.03г.) равнялась 20 тыс. руб. за акцию. Сумма кредита составляет 75 % курсовой стоимости залога. Кредит выдается под 20 % годовых. За обслуживание долга банк взимает 1 % от номинальной суммы кредита. Определить размер кредита, полученного клиентом банка. Решение. Курсовая стоимость кредита: 200-20 тыс. руб. = 4,0 млн. руб. Номинальная величина кредита: 4,0-0,75 = 3,0 млн. руб. Сумма процентных платежей за 92 дня составит: 3,0*92/360*0,2 = 0.153 млн. руб. Затраты банка по обслуживанию долга: 3,0*0,01 = 0,03 млн. руб. Фактическая задолженность клиента на дату погашения ссуды равна: 3,0 + 0,153 + 0,03 = 3,183 млн. руб. Чтобы снизить риск банк обычно взыскивает процентный платеж и плату за обслуживание долга предварительно. Тогда остаток основного долга клиента на 15.06.03 составил 3,0 млн. руб. А сумма кредита, полученного клиентом, составляет величину 3,0 - (0.153 + 0,03) = 2,817 млн. руб. Пример 5.10. Депозит в размере 2 млн. руб. внесен в банк на 3 года под 10% годовых под сложные проценты. Начисление процентов производится ежеквартально. Определить наращенную сумму. Решение. S(Т) = 2*(1+0.1/4)3*4=2 *1,3449 = 2689,76 тыс. руб. Если начисления ежемесячные, то получим: S(T)=2*(1+0.1/12) 3*12=2696.363 тыс. руб. Пример 5.11. Стоимость транспортируемого груза составляет 200 млн. руб. Вероятность транспортной аварии – 0,05; а страховой тариф составляет 3% от страховой суммы. Страховать или не страховать груз при перевозке? Решение. Затраты владельца груза на его страхование составляют : 200*0.03 = 6 млн. руб. Тогда при страховании груза выигрыш владельца составит:200*0.05+(- 6)*0.95 = 4.3 млн. руб. > 0.Следовательно, при данном страховом тарифе страховать груз выгодно. 6. ФОРМИРОВАНИЕ ОПТИМАЛЬНОГО ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ 6.1. ПРОБЛЕМА ВЫБОРА ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ Под портфелем мы будем понимать набор инвестиций в ценные бумаги, обращающиеся на финансовом рынке. В соответствии с этим основное внимание следует уделить понятиям инвестиционной среды и инвестиционного процесса. Инвестиционная среда характеризуется типами бумаг, обращающихся на рынке, условиями их приобретения и продажи. Понятие инвестиционного процесса связано с тем, каким образом инвестор принимает решения при выборе бумаг, объемов и сроков вложения. Прежде чем более детально обсудить эти понятия, следует определить термин «инвестиции». В наиболее широком смысле слово «инвестировать» означает: «расстаться с деньгами сегодня, чтобы получить большую их сумму в будущем». Два фактора обычно связаны с данным процессом - время и риск. Отдавать деньги приходится сейчас и в определенном количестве. Вознаграждение поступает позже, если поступает вообще, и его величина заранее неизвестна. В некоторых случаях важнейшим фактором будет время (например, для государственных облигаций). Управление инвестициями представляет собой процесс управления денежными средствами, или используют термин управление портфелем. Специалистов, управляющих инвестиционными портфелями, называют инвестиционными, денежными или портфельными менеджерами. Все инвесторы делятся на индивидуальных или розничных и институциональных. Первая категория состоит из частных (физических) лиц, инвестирующих собственные средства. Вторая включает страховые компании, депозитные институты (например, банки, сберегательные и кредитные ассоциации), инвестиционные компании и различные фонды: пенсионные, накопительные и др. Целесообразно различать реальные и финансовые инвестиции. Реальные инвестиции обычно включают инвестиции в какой-либо тип материально осязаемых активов, таких, как земля, оборудование, заводы. Финансовые инвестиции представляют собой контракты, записанные на бумаге, такие, как обыкновенные акции и облигации. В примитивных экономиках основная часть инвестиций относится к реальным, в то время как в современной экономике большая часть инвестиций представлена финансовыми инвестициями. Высокое развитие институтов финансового инвестирования в значительной степени способствует росту реальных инвестиций. Как правило, эти две формы являются взаимодополняющими, а не конкурирующими. Процесс управления инвестициями можно разбить на следующие пять этапов: формулировка инвестиционных целей, зависящая от задач финансового института. Формирование инвестиционной политики для достижения выбранных целей. Выбор портфельной стратегии, соответствующей целям клиента и инвестиционной политике. Выбор активов, заключающийся в определении тех активов, которые будут включены в портфель. 5. Измерение и оценка эффективности инвестиций. Остановимся более подробно на некоторых этапах. Второй этап начинается с принятия решения о распределении имеющихся фондов между основными классами активов, состоящих из различного типа ценных бумаг: казначейские векселя, долгосрочные облигации, обыкновенные акции. Портфельные стратегии можно разделить на активные и пассивные. Активные портфельные стратегии используют доступную информацию и методы прогнозирования для повышения эффективности инвестиций по сравнению с простой диверсификацией. Наиболее существенным моментом для всех активных стратегий является прогнозирование факторов, способных повлиять на инвестиционные характеристики данного класса активов. Например, активные стратегии при работе с портфелями обыкновенных акций могут включать прогнозирование будущих доходов, дивидендов или показателя отношения цены к доходу. Облигационные стратегии основываются на прогнозировании будущего уровня процентных ставок, а стратегии работы с иностранными ценными бумагами - на ожидаемых обменных курсах валют. Пассивные портфельные стратегии требуют минимума информации о будущем, В основе таких стратегий лежит диверсификация портфеля, обеспечивающая максимальное соответствие его доходности выбранному рыночному индексу. Пассивные стратегии основываются на предположении, что вся доступная информация на рынке отражается в рыночных котировках ценных бумаг. При выборе активов необходимо указать соответствующие количественные характеристики, т.е. какие доли капитала инвестировать в различные типы и виды ценных бумаг. На этом этапе менеджер стремится сформировать эффективный портфель. Этот портфель представляет собой портфель, имеющий либо наибольшую ожидаемую доходность при заданном уровне риска, либо наименьший риск при заданной ожидаемой доходности. При оценке эффективности инвестиций производится вычисление реализованной доходности портфеля и сопоставление полученного результата с выбранным базисным показателем. Базисным показателем в данном случае служит некоторая количественная характеристика поведения заранее выбранного набора ценных бумаг. В качестве базисного показателя может быть выбран любой из общеизвестных фондовых индексов, например индекс Standard & Poor's500 (S & P500), или один из облигационных индексов, публикуемых ведущими консалтинговыми компаниями. Важнейшую роль в управлении инвестициями играет теория оптимального портфеля, связанная с проблемой выбора эффективного портфеля, максимизирующего ожидаемую доходность при некотором, приемлемом для инвестора уровне риска. Теоретико-вероятностные методы позволяют дать определения «ожидаемой доходности» и « риска» портфеля, а статистические данные - получить оценку этих характеристик. При построении эффективного портфеля будем считать, что инвестор избегает риска, т.е. из двух вариантов инвестирования с одинаковой ожидаемой доходностью, но различными уровнями риска он выберет тот, риск которого меньше. Если инвестор стоит перед выбором одного из эффективных портфелей, то оптимальным портфелем будет наиболее предпочтительный из них. Гарри Марковиц считается отцом современной «портфельной теории», касающейся методов сбалансирования рисков и экономической выгоды при выборе направлений рискованных инвестиций. В своей программной статье «Выбор портфеля» (PortfolioSelection), опубликованной в 1952 году в JournalofFinance, он разработал математическую модель, демонстрирующую, как инвесторы могут максимально снизить риск при заданной ставке доходности. Модель Марковица входит в основы финансов и широко применяется на практике специалистами по управлению инвестиционными портфелями. В 1952 г. Гарри Марковиц опубликовал фундаментальную работу, которая является основой подхода к инвестициям с точки зрения современной теории формирования портфеля. Подход Марковица начинается с предположения, что инвестор в настоящий момент времени имеет конкретную сумму денег для инвестирования. Эти деньги будут инвестированы на определенный промежуток времени, который называется периодом владения. В конце периода владения инвестор продает ценные бумаги, которые были куплены в начале периода, после чего либо использует полученный доход на потребление, либо реинвестирует доход в различные ценные бумаги (либо делает то и другое одновременно). Таким образом, подход Марковица может быть рассмотрен как дискретный подход, при котором начало периода обозначается t = 0, а конец периода обозначается t= 1. В момент t = 0 инвестор должен принять решение о покупке конкретных ценных бумаг, которые будут находиться в его портфеле до момента t = 1. Поскольку портфель представляет собой набор различных ценных бумаг, это решение эквивалентно выбору оптимального портфеля из набора возможных портфелей. Поэтому подобную проблему часто называют проблемой выбора инвестиционного портфеля. Принимая решение в момент t = 0, инвестор должен иметь в виду, что доходность ценных бумаг (и, таким образом, доходность портфеля) в предстоящий период владения неизвестна. Однако инвестор может оценить ожидаемую (или среднюю) доходность различных ценных бумаг, основываясь на некоторых предположениях, а затем инвестировать средства в бумагу с наибольшей ожидаемой доходностью. Марковиц отмечает, что это будет в общем неразумным решением, так как типичный инвестор хотя и желает чтобы «доходность была высокой», но одновременно хочет, чтобы «доходность была бы настолько определенной, насколько это возможно». Это означает, что инвестор, стремясь одновременно максимизировать ожидаемую доходность и минимизировать неопределенность, т.е. риск, имеет две противоречащие друг другу цели, которые должны быть сбалансированы при принятии решения о покупке в момент t = 0. Подход Марковица к принятию решения дает возможность адекватно учесть обе эти цели. Следствием наличия двух противоречивых целей является необходимость проведения диверсификации с помощью покупки не одной, а нескольких ценных бумаг. В 1990 году Нобелевская премия по экономике была присуждена ученым Гарри Марковицу, Мертону Миллеру и Уильяму Шарпу за научный вклад, оказавший огромное влияние на развитие теории и практики финансов. Далее вашему вниманию предлагается краткое описание их работ. Уильям Шарп использовал результаты исследований Г. Марковица в качестве отправного пункта для дальнейших исследований, в ходе которых определил влияние модели Марковица на цены финансовых активов. Сделав допущение, что в любой момент времени цены на финансовые активы будут изменяться, чтобы обеспечить равновесие спроса и предложения каждого рискованного актива, он продемонстрировал, что ожидаемые показатели доходности рискованных активов должны иметь очень специфическую структуру («Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk», JournalofFinance, 1964) («Оценка акций. Теория рыночного равновесия в условиях риска»). Структура активов, выведенная в теоретических построениях Шарпа, в наши дни очень широко используется в качестве основы для регулирования степени риска во многих областях теории и практики финансов. Основной вклад Мертона Миллера выражается главным образом в развитии теории корпоративных финансов. Совместно с другим ученым, Франко Модильяни (также лауреатом Нобелевской премии в сфере экономики), Миллер занимался вопросами дивидендной политики и политики заимствования фирм. Этим проблемам ученые посвятили серию статей, началом которой была работа «The Cost of Capital, Corporation Finance, and the Theory of Investment» («Стоимость капитала, корпоративные финансы и теория инвестирования»), опубликованная в AmericanEconomicReviewв 1958 году. Главным их открытием стало то, что они предпожили теоретикам и практикам в области финансов обратить особое внимание на то, каким образом на общую стоимость любой фирмы влияет ее дивидендная и финансовая политика. Так называемая теория М&М (теория Модильяни - Миллера), изложенная в их совместных работах, является основой современной теории корпоративных финансов. В 1997 году Нобелевская премия по экономике была вновь присуждена специалистам в области финансов. На этот раз ее лауреатами стали Роберт К. Мертон и Майрон Шоулз. Комитет по назначению лауреатов выдвинул для присуждения премии еще одного ученого, Фишера Блэка, чья преждевременная смерть в возрасте 57 лет в 1995 году, помешала ему разделить эту честь. Эти три человека открыли математическую формулу для вычисления стоимости опционов и других производных ценных бумаг, которая оказала огромное влияние на теорию и практику финансов. Она широко известна под названием формулы Блэка - Шоулза (Black-Scholes option pricing formula). Портфельная теория представляет собой статистический анализ, выполняемый с целью выбора оптимальной стратегии управления риском. С какой бы точки зрения ни рассматривать - домохозяйства, компании или иного экономического субъекта, - использование портфельной теории заключается в выработке и оценке компромисса между доходом и издержками, связанными с уменьшением риска, что необходимо для определения оптимального образа действия данного субъекта. Если речь идет о семье, то в качестве определяющего критерия принимаются предпочтения в области потребления и риска. И хотя предпочтения изменяются со временем, механизмы и причины этих изменений не рассматриваются в портфельной теории. Портфельная теория акцентирует внимание на том, как из нескольких финансовых вариантов выбрать такие, чтобы максимизировать данные предпочтения. В целом оптимальный вариант выбора предполагает оценку компромисса между получением более высокой ставки доходности и увеличением степени риска инвестиций. Однако отнюдь не каждое решение, направленное на сокращение риска, приводит к уменьшению ожидаемой доходности. Бывают обстоятельства, при которых обе стороны, подписывающие контракт о переносе риска, могут уменьшить уровень своего риска, заплатив за это ровно столько, сколько стоит юридическое оформление контракта. Например, покупатель и продавец дома могут договориться и установить фактическую цену дома в момент подписания контракта, хотя сама передача прав собственности состоится только через три месяца. Такое соглашение служит одним из примеров форвардного контракта. Соглашаясь заключить такой контракт, обе стороны избавляются от неопределенности, связанной с колебаниями цен на рынке жилья в ближайшие три месяца. Таким образом, когда противоположные стороны воспринимают риск одного и того же события с разных точек зрения, для обеих лучше всего совершить перенос риска с помощью контракта, причем ни одной из сторон не придется нести значительные расходы. Решения, связанные с управлением риском, принятие которых не влечет за собой затрат, являются скорее исключением из правил, чем нормой. Обычно для сокращения степени риска требуется сбалансировать необходимые для этого расходы и получаемые выгоды. Такой компромисс, пожалуй, более всего очевиден в решениях, принимаемых домохозяйством по поводу распределения его средств среди таких активов, как акции, ценные бумаги с фиксированным доходом и жилье. Первые формальные модели портфельной теории были разработаны для выработки именно этого типа решений в управлении риском. В этих моделях для вычисления соотношения между риском инвестиций и их ожидаемой доходностью используется распределение вероятностей. Ожидаемая доходность портфеля ценных бумаг определяется как среднее значение распределения вероятностей, а риск - как стандартное отклонение возможных значений доходности от ожидаемого. 6.2. ДИВЕРСИФИЦИРОВАННЫЙ ПОРТФЕЛЬ В экономике часто встречаются ситуации, когда субъект (физическое лицо или фирма) должен выбрать одну из альтернатив. Существует экономическая теория, которая занимается изучением процесса выбора, используя так называемую функцию полезности. Функция полезности описывает правило, по которому каждому из возможных вариантов выбора приписывается некоторое числовое значение. Чем больше это значение, тем больше «полезность» данного варианта выбора. Говоря проще, в теории портфеля функция полезности выражает предпочтения субъекта при определенных отношенях к риску и представлениях об ожидаемых доходностях. В графической форме функцию полезности отражают кривые безразличия. На рис. 6.1 они обозначены через и1,u2, из. На горизонтальной оси откладывается значение риска, а на вертикальной - ожидаемые доходности. Кривые представляют собой наборы портфелей с различными комбинациями риска и доходности. Точки одной такой кривой определяют значение риска и доходности для данного уровня полезности. Рассмотрим, например, два портфеля и и и* на кривой и1. Портфель и имеет большую доходность, но и больший по сравнению с u* риск. При этом инвестору безразлично, какой из них выбирать. Наклон кривой безразличия означает, что с ростом риска инвестор требует его компенсации большей доходностью. 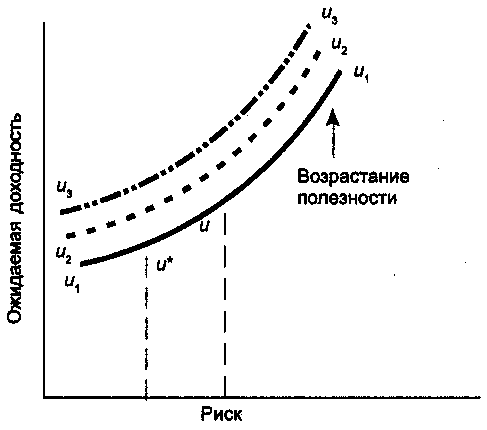 Рис. 6.1. Кривые безразличия Чем выше лежит кривая, тем больше полезность, поскольку по вертикали отложены доходности. Таким образом, из трех кривых на рис. 6.1 кривая u3 имеет наибольшую полезность, а и1- наименьшую. Все портфели, лежащие на одной заданной кривой безразличия, являются равноценными для инвестора. При формировании портфеля следует различать рисковые и безрисковые активы. Рисковые активы - это активы, доходность которых в будущем неопределенна. Предположим, что инвестор покупает акции компании и планирует держать их один год. В момент покупки он не знает, какой доход получит в конце срока. Это зависит от стоимости акции через год и дивидендов, которые компания выплачивает в течение года. Поэтому эти акции, так же как и акции других компаний, - это рисковые активы. Даже ценные бумаги, выпускаемые правительством США, являются рисковыми. Допустим, например, что инвестор купил правительственные облигации со сроком погашения 30 лет. Он не знает, какой доход получит, если продержит их всего один год, Дело в том, что на стоимость облигаций в течение года влияет изменение процентной ставки. Тем не менее активы, будущая доходность которых известна в момент погашения, существуют. Такие активы называются безрисковыми активами. Как правило, это краткосрочные правительственные облигации. Допустим, инвестор покупает казначейские векселя США сроком погашения один год и планирует держать их до погашения. В таком случае относительно доходности этих бумаг нет никакой неопределенности. Инвестор знает, что в день их погашения правительство выплатит определенную сумму (номинал), погашающую долг. Обратите внимание на то, как отличается эта ситуация от предыдущей, хотя и в первом, и во втором случае ценные бумаги являются государственными. Принимая решение о приобретении портфеля, инвестор должен обращать внимание на ожидаемую доходность и стандартное отклонение каждого портфеля. Ожидаемая ставка доходности (среднее значение доходности) определяется как сумма всех возможных ставок доходности, умноженных на соответствующую вероятность их получения: 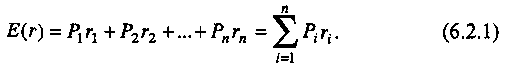 Предположим, что ожидаемая доходность акций А – rA = 10 %, а акций B – rB = 15 %. Если весь капитал вложить в акции А, то ожидаемая доходность портфеля rП = rА = 10 %. Если инвестировать капитал только в акции В,то ожидаемая доходность инвестиции составит: rП= rB = 15%. При инвестировании капитала в акции равными долями ожидаемая доходность портфеля будет равна средневзвешенной из доходности акций: rП = 0,5 • 10 % + 0,5 • 15 % = 12,5 %. По истечении года фактические значения доходности акций А и В, аследовательно, и портфеля в целом, возможно, будут не совпадать с их ожидаемыми значениями. Рискованность одного актива измеряется дисперсией или средним квадратическим отклонением доходов по этому активу, а риск портфеля - дисперсией или средним квадратическим отклонением доходов портфеля. Если для создания портфеля ценных бумаг инвестировать деньги в какой-то один вид финансовых активов, то инвестор оказывается зависимым от колебания его курсовой стоимости. Поэтому следует вкладывать капитал в акции нескольких компаний, хотя понятно, что эффективность также будет зависеть от курсовых колебаний, но уже не каждого курса, а усредненного, который, как правило, колеблется меньше, поскольку при повышении курса одной из ценных бумаг курс другой может понизиться, и колебания могут взаимно погаситься. Такой портфель ценных бумаг, содержащий самые разнообразные типы ценных бумаг, называется диверсифицированным портфелем. Хотя подобный портфель значительно снижает диверсификационные (несистематические) риски, но полностью устранить инвестиционный риск нельзя, так как при вложении капиталов присутствуют еще и недиверсифицированные или систематические риски, присущие конкретной экономической системе в целом или отдельному рынку и не поддающиеся диверсификации. Систематический риск обусловлен общим состоянием экономики, который связан с такими факторами, как: война, инфляция, глобальные изменения налогообложения, изменение денежной политики и т.п., и связан с изменениями цен на акции, их доходностью, текущим и ожидаемым процентом по облигациям, ожидаемыми размерами дивиденда, вызванными общерыночными колебаниями. Однако чтобы измерить риск портфеля, нам нужно не только знать вариацию доходов отдельных ценных бумаг, но и степень, с которой доходы пар ценных бумаг колеблются вместе. Нам необходимо знать ковариацию или же корреляцию доходов каждой пары активов в портфеле. Риск портфеля, измеряемый через дисперсию, рассчитывается как взвешенная сумма ковариаций всех пар активов в портфеле, где каждая ковариация взвешена на произведение весов каждой пары соответствующих активов и дисперсия данного актива рассматривается как ковариация актива с самим собой. Дисперсия или вариация случайной величины служит мерой разброса ее значений вокруг среднего значения. Для доходности (как случайной величины) вариация, оценивающая степень отклонения возможных конкретных значений от средней или ожидаемой доходности, служит мерой риска, связанного с данной доходностью. Формула для определения вариации доходности i-го актива, записывается следующим образом: 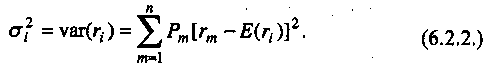 Вариация учитывает не только размер отклонений возможных значений доходности от среднего, но и вероятность такого отклонения. В этом смысле дисперсия указывает меру неопределенности в ожиданиях инвестора, который оценивает будущую доходность как среднюю по всем возможным значениям. Это обстоятельство и позволило Марковицу считать дисперсию доходности мерой риска инвестиций. Однако, можно привести два довода против использования вариации в качестве меры риска. Первый - вариация учитывает отклонение в обе стороны по отношению к среднему значению. Действительно, реализованная доходность может быть как выше, так и ниже среднего значения, при этом первый случай также вносит вклад в величину вариации и, следовательно, риска. Инвестор же не расценивает превышение реальной доходности над ожидаемой как неприятный результат. Напротив, он только приветствует такой исход дела. Поэтому многие исследователи считают, что при измерении риска не должны рассматриваться случаи, когда возможная доходность выше ожидаемой. Марковиц понимал этот недостаток вариации и предлагал меру риска, которая учитывала лишь случаи снижения доходности по отношению к среднему значению. Эту меру называют полувариацией. Полувариация рассчитывается как обычная вариация кроме тех случаев, когда доходность выше ожидаемой доходности. Однако сложности вычисления, связанные с использованием полувариации, привели к тому, что в своих работах Марковиц был вынужден ограничиться обычной вариацией. В настоящее время при измерении риска снижения стоимости ценной бумаги финансисты-практики пользуются обоими понятиями. Второй довод, относящийся к недостаткам вариации как меры риска, состоит в том, что она нечувствительна к асимметричности распределения отклонений от среднего значения. В случае несимметричных распределений приходится пользоваться другими характеристиками типа коэффициента асимметрии и т.п. Марковиц не рассматривал подобные характеристики в своей теории. Использование вариации можно оправдать, основываясь на эмпирических исследованиях, подтверждающих относительную симметричность статистических распределений доходностей акций. Поскольку считается, что для принятия решения инвестор рассматривает только ожидаемую доходность и вариацию, теория портфеля в формулировке Марковича получила название двухпараметрической модели. При вычислении стандартного отклонения портфеля пользуются понятием ковариации. Ковариация - это статистическая мера взаимодействия двух случайных переменных. То есть это мера того, насколько две случайные переменные, такие, например, как доходности двух ценных бумаг iиj, зависят друг от друга. Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону, например лучшая, чем ожидаемая, доходность одной из ценных бумаг должна, вероятно, повлечь за собой лучшую, чем ожидаемая, доходность другой ценной бумаги. Отрицательная ковариация показывает, что доходности имеют тенденцию компенсировать друг друга, например лучшая, чем ожидаемая, доходность одной ценной бумаги сопровождается, как правило, худшей, чем ожидаемая, доходностью другой ценной бумаги. Относительно небольшое или нулевое значение ковариации, показывает, что связь между доходностью этих ценных бумаг слаба либо отсутствует вообще. В общем случае вычисление стандартного отклонения портфеля, состоящего из и ценных бумаг, требует двойного суммирования п ценных бумаг, для чего необходимо сложить п членов; 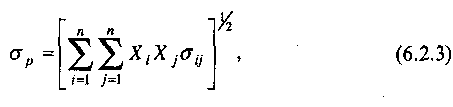 где σijобозначает ковариацию ценных бумаг i и j Очень близкой к ковариации является статистическая мера, известная как корреляция. На самом деле, ковариация двух случайных переменных равна корреляции между ними умноженной на произведение их стандартных отклонений: где рijобозначает коэффициент корреляции между доходностью на ценную бумагу i и доходностью на ценную бумагу. Коэффициент корреляции нормирует ковариацию для облегчения сравнения с другими парами случайных переменных. Коэффициент корреляции всегда лежит в интервале между -1 и +1. Если он равен -1, то это означает полную отрицательную корреляцию, если +1 - полную положительную корреляцию. В большинстве случаев он находится между этими двумя экстремальными значениями. Рисунок 6.2 (а) представляет собой точечную диаграмму до-ходностей гипотетических ценных бумаг А и В, когда корреляция между двумя этими ценными бумагами, полностью положительна. Заметим, что все точки лежат на прямой наклонной линии, идущей из левого нижнего квадранта в правый верхний. Это означает, что когда одна из двух ценных бумаг имеет относительно высокую доходность, тогда и другая ценная бумага имеет относительно высокую доходность. Соответственно, когда одна из двух ценных бумаг имеет относительно низкую доходность, тогда и другая имеет относительно низкую доходность. Однако корреляция между доходностями двух различных ценных бумаг будет абсолютно отрицательной, когда точечная диаграмма показывает, что точки лежат именно на прямой наклонной линии, идущей из левого верхнего квадранта в правый нижний, как это показано на рис. 6.2 (б). В данном случае можно сказать, что доходности двух ценных бумаг изменяются противоположно друг другу. То есть когда одна из ценных бумаг имеет относительно высокую доходность, другая имеет относительно низкую доходность. Особый случай возникает, когда точечная диаграмма доходности ценных бумаг показывает разброс точек, который даже приблизительно не может быть представлен прямыми наклонными линиями. В таком случае делается вывод о некоррелированности доходностей, т.е. о равенстве нулю коэффициента корреляции. Рис. 6.2 (в) представляет данный пример. В такой ситуации, когда одна из ценных бумаг имеет относительно высокую доходность, другая может иметь и относительно высокую, и относительно низкую, и среднюю доходности.  Рис. 6.2.Доходность двух ценных бумаг Теперь на конкретном примере рассмотрим понижающий риск эффект диверсификации. В центре внимания стратегии диверсификации Марковица прежде всего находится уровень ковариации доходностей активов портфеля. Ключевой вклад Марковица состоит в постановке вопроса о риске активов как составляющих единого портфеля, а не отдельно взятых единиц. Данная стратегия, стремясь к максимально возможному снижению риска при сохранении требуемого уровня доходности, состоит в выборе таких активов, доходности которых имели бы возможно меньшую положительную корреляцию. Именно учет взаимной корреляции доходностей активов с целью снижения риска отличает стратегию диверсификации Марковича от стратегии наивной диверсификации. Способ диверсификации Марковица и важность корреляции активов можно проанализировать на примере портфеля из трех активов. Для этого мы сначала покажем общую взаимосвязь ожидаемого риска портфеля из трех активов и корреляции их доходностей. Затем мы изучим влияние комбинирования активов с различными корреляциями на риск всего портфеля. Портфель составлен из трех видов ценных активов А, В, С. Веса, с которыми каждый актив представлен в портфеле, равны Vа = 50 % = 0,5, Vb = 30 % = 0,3 и Vc = 20 % = 0,2. Доходы по каждому из активов представлены в табл. 6.1. Таблица 6.1 Исходные данные  Для нахождения связи между доходами каждой ценной бумаги определяем ковариацию (корреляцию) каждой пары активов по формуле  и ковариацию актива с самим собой  Ковариации доходов по всем возможным парам активов отображаем в ковариационной матрице: 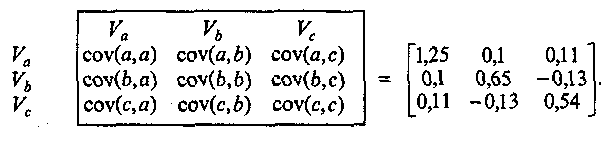 Риск портфеля находится по формуле: 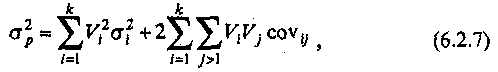 где n - объем выборочной статистики по годам, k- число активов. Для вычисленной ковариационной матрицы найдем, что σ2р = 0,429 и σр = 0,65 = 65 %, Отсюда видно, что риск портфеля лишь несколько ниже риска отдельных активов и средневзвешенного риска отдельных активов равного, Составим новый портфель активов, заменив актив А на актив D, оставив его долю прежней, т.е. Vd =Va = 50 % = 0,5, а доходность актива D представлена в табл. 6.1. Составляем новую ковариацию доходов: 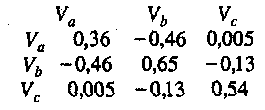 Риск портфеля рассчитанный по формуле (6.2.7), равен σp = 0,132 = 13,2 %. Риск этого портфеля в пять раз меньше, чем предыдущего. Это объясняется снижением коррелированное™ активов Dи С и наличием отрицательной ковариации активов Dи В. Стоимость портфеля даже несколько повысилась, так как средний доход по активам Dравен 12 %, а по активам А – 11 %. Подобная операция служит базой для хеджирования, когда отрицательная корреляция достигается продажей позиции по инструменту (актив А), который имеет высокую степень положительной корреляции и приобретением другого актива D. Анализ значений риска рассмотренных портфелей показывает, что риск портфеля меньше, чем средняя взвешенная рисков отдельных ценных бумаг и среднее квадратическое отклонение портфеля падает, когда снижается степень корреляции пар активов. Общий риск ценной бумаги, находящейся в изоляции, больше, чем у той же ценной бумаги, находящейся в портфеле. Комбинация активов со слабой корреляцией понижает риск портфеля. Эффективная диверсификация достигается Не просто добавлением активов к портфелю, а добавлением таких активов, доходы которых имеют самые низкие корреляции, а лучше и отрицательные, с активами, присутствующими в портфеле. Рассмотрим выражение (6.2.7), Представим, что имеется очень большое количество активов, доступных для инвестиций, скажем индекс из 100 или 500 акций. Допустим также, что все доходы по активам независимы. Выражение (6.2.7) сократится до следующего:  Этот пример наглядно показывает эффект диверсификации Марковича. Данное явление иногда называют «чудом диверсификации». Стратегия диверсификации Марковича предполагает, что с увеличением корреляции (ковариации) доходностей активов, составляющих единый портфель, возрастает вариация (а следовательно, и стандартное отклонение) доходности этого портфеля. «Чудо» проявляется при отрицательной корреляции ожидаемых доходностей активов. Прекрасно то, что инвестор может снизить риск портфеля, удерживая его ожидаемую доходность при помощи сочетания активов с низкой (желательно отрицательной) корреляцией. Плохо лишь то, что активов с малой и отрицательной корреляцией существует совсем немного. Таким образом, задача превращается в поиск среди многочисленных активов таких, портфель из которых имел бы минимальный риск при заданном уровне доходности или, наоборот, при заданном уровне риска имел бы наибольшую доходность. Так как предполагается, что доходы по активам независимы, ковариации равняются нулю. Теперь предположим, что равные суммы инвестированы в каждый из n активов, тогда веса каждого станут равными 1/п, и дисперсия портфеля примет вид: 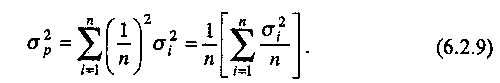 Выражение в прямоугольных скобках является средней дисперсией активов в портфеле. В то время как число активов (n) в портфеле становится больше, 1/n уменьшается, и дисперсия портфеля снижается, приближаясь в пределе к нулю. Однако в действительности не все доходы по активам независимы, особенно, когда мы рассматриваем активы, принадлежащие к одному классу, например, акции и облигации. У большинства активов будет присутствовать некоторый уровень ковариаций, Отсюда на практике равенство (6.2.9) превращается в следующее: 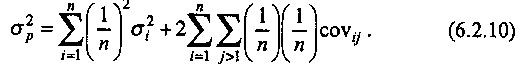 Это можно представить так: 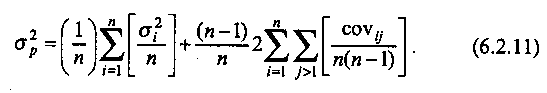 Первый член равенства представляет собой среднюю дисперсию, уже встречавшуюся выше в выражении (6.2.9), а второй - это тоже средняя, т.е. сумма ковариаций, деленная на число кова-риаций п(п - 1). Выражение (6.2.11), таким образом, может быть упрощено до: Эта формула помогает объяснить, что происходит с риском портфеля, когда в него включено большое количество активов. Когда число активов в портфеле увеличивается, 1/n уменьшается, и, таким образом, его произведение на среднюю дисперсию приближается к нулю. Однако (n - 1)/n стремится к единице при увеличении п, отсюда второе слагаемое правой части выражения (6.2.12) приближается к средней ковариации. Следовательно, когда портфель диверсифицирован включением большого числа активов, дисперсия портфеля приближается к средней ковариации отдельных активов. Значит, общий риск ценной бумаги, находящейся в изоляции, больше, чем у той же ценной бумаги, находящейся в портфеле. Комбинация активов со слабой корреляцией понижает риск портфеля. Таким образом, общий риск состоит из двух частей: а) тот риск, который может быть исключен диверсификацией (несистематический риск, также известный как случайный или остаточный риск) и б) тот элемент риска, который не может быть исключен с помощью диверсификации (систематический риск, также известный как рыночный риск). В заключении рассмотрим пример составления ковариационной матрицы. Пусть рынок может находиться в одном их трех состояний: I, II и III. Известны вероятности этих состояний и доходности трех активов в процентах. 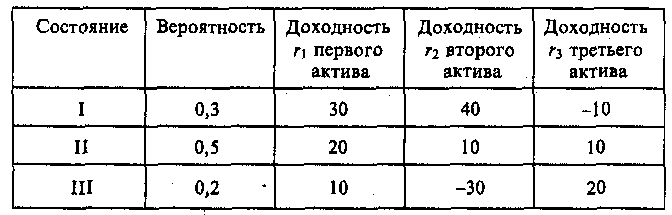 Находим математические ожидания доходности каждого из активов по формуле (6.2.1): 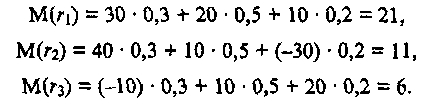 Находим коэффициенты Kijковариационной матрицы: 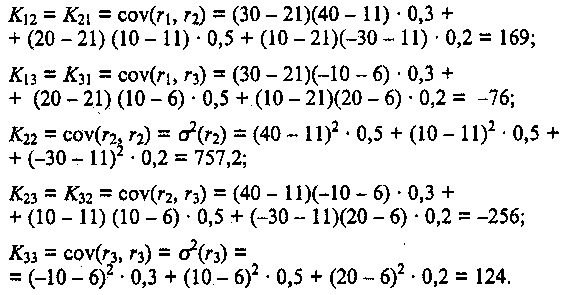 Эти результаты сведем в ковариационную матрицу: 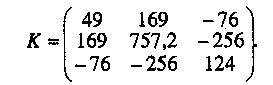 Стандартные отклонения по каждому из активов равны: Определяем коэффициенты корреляции: 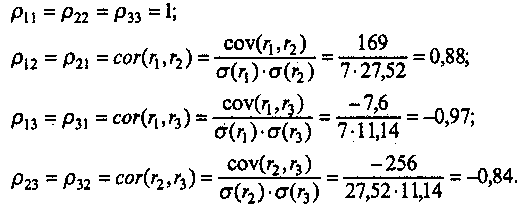 Коэффициенты корреляции записываем в виде корреляционной матрицы: 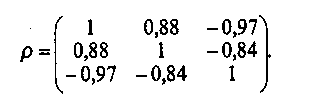 |
