ЛЕКЦИИ Финансовая среда предпринимательства и предпр. риски. Тезисы лекций по дисциплине Финансовая среда предпринимательства и предпринимательские риски

• Название: Тезисы лекций по дисциплине Финансовая среда предпринимательства и предпринимательские риски
• Дата: 13.03.2023
• Размер: 1.82 Mb.
• Имя файла: ЛЕКЦИИ Финансовая среда предпринимательства и предпр. риски.doc
• Тип: Тезисы; #985552
• страница: 6 из 25

По неравенству Чебышева имеем

Р (R<r) = Р( - (R-m)> m- r ) < Р ( ׀R - m׀> m – r ) < ơ² / (m –r)² .

Для того, чтобы шанс разориться был не более одного из девяти, достаточно выполнить условие ² < (1/9) (m –r)² или m> r + 3 ( правило трех сигм).

Пример 5.2. Инвестор вкладывает в акции с параметрами (m, ) часть своего капитала, оставляя остальное на сбережения (x₀) под процент r₀ , выплачиваемый ему. Какова вероятность разорения инвестора?

Решение. Если К – начальный капитал, а x₀ К – оставшаяся на сбережении часть, то разорение возможно, если x₀ К (1+r₀ ) + (1- x₀) К (1+ R) < 0, т.е. если R< - ( 1+ x₀r₀ ) / (1- x₀ ).

Оценка по Чебышеву дает шанс разорения меньший 1/9 , если

/ ( m + (1+ x₀r_r0 ) / ( 1- x₀ )) < 1/3 , т.е., если

m> -(1+ x₀r₀ )/(1- x₀ ) + 3ơ.

Заметим, что оценка Чебышева, как правило, предусматривает большой запас. Например, если заведомо известно, что колебания в обе стороны от m равновероятны, то оценки шансов на разорение уменьшатся почти в 5 раз: вместо одного случая из 9 гарантируется, что разорение произойдет не чаще, чем в одном случае из 40.

Еще одной интересной мерой риска является вероятность превышения потерь над располагаемым капиталом или его частью. Более общий подход к оценке меры риска заключается во введении функции полезности.

Функция полезности в экономической теории позволяет соизмерить потребительский эффект различных физически несоизмеримых товаров. Соизмеримость ценных бумаг невозможна: нельзя сказать, какая из случайных эффективностей больше или меньше, а следовательно, нельзя сказать, какая из ценных бумаг или какой портфель предпочтительнее.

Установление любой меры риска является попыткой преодолеть это противоречие, характеризуя случайную величину одним числом. В общей теории риска принято вводить такие числа Z с помощью соотношения Z = М (Ф (R) ), где Ф – та или иная функция, называемая функцией полезности.

Если Ф(R) = R, то Z = m_R , т.е. случайность характеризуется только ожидаемым значением. Если же Ф(R) = R – ξ (R- m_R)² , где ξ – заданное число, то Z = m_R- ξ _R² , т.е. такая мера случайной величины учитывает и ожидаемое значение, и вариацию (дисперсию).

Квадратичная функция вида Ф(R) = R – ξ (R- m_R)² наиболее широко используется в теории рынка ценных бумаг. Ее интерпретация следующая. Инвестор считает полезным для себя увеличить значение эффективности от ожидаемого значения. Чем больше ξ, тем больше проявляется тенденция избегания риска, связанного со случайностью. Величину ξ можно считать числовой мерой тенденции инвестора избегать риск, а обратную ей - числовой мерой его склонности к риску.

Принятие ожидаемой функции полезности Z = m_R- ξ _R² в качестве критерия выбора решения – это попытка совместить два критерия: ожидаемое значение какой – либо величины и ее вариацию (дисперсию).

Вероятность неразорения при начальном капитале К₀ также может быть введена с помощью специальной функции полезности:

Ф(R) = .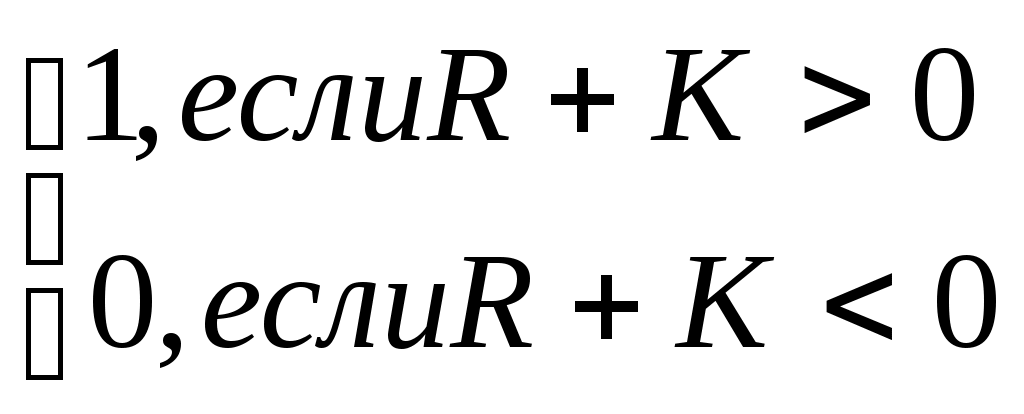

Таким образом, применяя различные функции полезности можно описать любые варианты оценки случайности ситуации в виде ожидаемого значения такой функции.

Теория риска как раз и занимается предпочтениями (правилами сравнения) случайных величин (СВ) будущих доходов R.

Правило первого стохастического доминирования (предпочтения) гласит, что если при любом состоянии природы СВ R₁не меньше СВ R₂ , то СВ R₁не хуже СВ R₂ , т.е._,если для функций распределенияF₁(r) и F₂(r) для всех rвыполняется соотношение F₁(r) ≤ F₂(r), F₁(r) не хуже F₂(r).

С точки зрения функции полезности можно утверждать, что СВ R₁ «лучше» СВ R₂ тогда, когда Ф (R₁ ) > Ф (R₂ ).

На практике используются различные функции полезности.

5.2. Управление рисками

Золотое правило инвестиционной политики гласит о том, что доход от вложений в ценные бумаги всегда прямо пропорционален риску, на который готов идти инвестор ради получения желаемого дохода.

Основными методами борьбы с рисками являются следующие:

1. 
   Диверсификация рисков. Народная мудрость гласит: «Никогда не держите ваши сбережения на одном банковском счете и никогда не делайте ставку на одно, даже самое выгодное для вас дело». Диверсификация – наличие в портфеле многих видов ценных бумаг с различной степенью риска, доходностью. Портфель – объединение двух или более ценных бумаг или активов.
   

Цель диверсификации – удержать риск портфеля инвестиций в пределах выбранной инвестиционной политики. Для эффективности диверсификации портфель должен состоять из некоррелированных бумаг. В целях диверсификации осуществляется рационирование кредита: банки устанавливают плавающие лимиты кредитования или кредитные потолки для заемщиков, сверх которых кредиты не представляются.

2. Хеджирование (англ. hedqing– ограждать ) – специальный случай диверсификации. Сознательно используя противоположную реакцию разных бумаг на одно и то же событие, получим хеджирование. Оно основано на таком распределении активов, чтобы суммарное влияние того или иного события на их стоимость оказалось нулевым (пример: покупка фьючерсного контракта; приобретение корпоративных бумаг, в частности, акций железной дороги и авиакомпаний и др.). Финансовые риски здесь сводятся к минимуму за счет взаимного погашения выигрыша и проигрыша.

3. Страхование, то есть перенесение убытков на другое лицо с
помощью некоторых гарантий. Страхующийся не уменьшает свои средние ­
потери, а лишь делает их предсказуемыми.

4. Распределение рисков между большим количеством лиц
("диверсификация наоборот"). Создаются разного рода совместные пулы или фонды, в которых участвуют много лиц. Убыток не уменьшается, но стано­вится более предсказуемым. Ограниченные возможности по страхованию крупных рисков, желание сбалансировать страховой портфель иногда вынуж­дают и страховщиков использовать в своей практике перестраховочные операции. В этом случае заключаются соглашения о взаимном обмене рисками, различающиеся по целям и видам страхования.

Профессиональные перестраховщики, используя в своей деятельно­сти принцип взаимности, стремятся решить двуединую задачу. С одной сто­роны, передать в перестрахование риски с большой вероятностью выплат по ним, с другой - попытаться провести качественный анализ и отбор рисков, принимаемых на основе взаимности.

5.Использование специальных механизмов торговли и исполне­ния сделок, снижающих вероятность потерь за счет усложнения и удорожа­ния технических процедур. К ним относятся резервирование средств на по­купку ценных бумаг (валюты), депонирование выставляемых на продажу
ценных бумаг, использование механизмов маржевых взносов в клиринговую плату и т.п. За счет замораживания средств они позволяют уменьшить риски
и сделать их регулируемыми. К этим механизмам можно отнести и гарантии
подписи собственника на документах, нотариальное заверение документов, хотя это сложная и достаточно дорогая процедура, не являющаяся гарантией
на все случаи. Иногда и брокеры имеют право заверять подписи своих клиен­тов на договорах и передаточных распоряжениях.

6.Комбинированные методы могут объединять вышеперечислен­ные и встречаются на практике в различных модификациях.

При управлении тем или иным видом риска часто рассматриваются
несколько стратегий или концепций поведения. Например, существует несколько концепций управления процентным риском.

1. Концепция максимальной маржи. Чем выше процентная маржа банка, тем ниже уровень процентного риска. Это означает, что маржа между процентными доходами от активов и процентными расходами по обязатель­ствам должна быть положительной.

2.Концепция "спрэд", при которой анализируется
разница между полученной средней ставкой, выплаченной по активам, и взвешенной средней ставкой, выплаченной по пассивам. Чем разница между этими двумя величинами больше, тем уровень процентного риска ниже. Дан­ные для анализа обычно берутся из статистической отчетности банка.

3. Концепция "разрыва", которая состоит в анализе несбалансиро­ванности активов и пассивов банка с фиксированной и плавающей процент­ной ставкой над пассивами с фиксированной ставкой в статике или за опреде­ленный период времени.

Основным методом снижения риска кредитования является анализ кредито- и платежеспособности заемщиков. 3десь используется целая система количественных и экспертных показателей, характеризующих рискованность финансового положения заемщиков, их платежеспособность, надежность и т.п. Золотое банковское правило гласит, что величена и сроки финансовых требований банка по активам должны соответствовать величине и срокам его обязательствам по пассивам.
Пример 5.3. Инвестор приобретает бескупонную облигацию с дисконтом 200 тыс. руб. и со сроком погашения через год. Одновременно инве­стор приобретает за свой счет страховку, гарантирующую ему получение суммы, равной номинальной стоимости облигации в случае, если эмитент не сможет выполнить свои обязательства по ее погашению. Причем, если эми­тент погашает облигацию, страховая компания возвращает инвестору 50 % от суммы страхового взноса. Рассчитайте размер страхового взноса, который обеспечил бы инвестору в случае выполнения эмитентом своих обязательств доходность, превышающую в три раза доходность, если эмитент отказывается погасить облигацию?

Решение. Пусть X- размер страхового взноса. Н– номинальная стоимость облигации. Тогда затраты инвестора независимо от выполнения эмитентом своих обязательств по погашению облигации составят Н - 200 + X.

Если эмитент облигацию погасит, то инвестор получит доход 200 - X + 0.5Х = 200 - 0.5Х. Действительно, Н + 0,5Х - ( Н-200+Х) = 200 - 0,5Х.Если эмитент облигацию не погасит, то инве­стор получит доход 200 - X. Так как Н -(Н-200+Х)= 200-Х. Поскольку затраты в обоих случаях равны, а до­ходность в первом случае в 3 раза превышает доходность во втором случае, то, следовательно, доход, полученный инвестором в случае погашения облига­ции превышает в три раза доход в альтернативном случае.

Отсюда найдем размер страхового взноса: 3*(200 - X) = 200 - 0.5*Х; 2.5*Х=400; Х= 160 тыс. руб.
Пример 5.4. Инвестор приобретает бескупонную облигацию с дисконтом. Облигация подлежит погашению через год. Одновременно инвестор приобретает за 180 тыс. руб. страховку, гарантирующую ему получение суммы, равной номинальной стоимости облигации, если эмитент не сможет вы­полнить свои обязательства по ее погашению. Если эмитент облигацию погасит, то страховая компания возвращает инвестору 80 % страхового взноса (плата за страховку). Рассчитайте размер дисконта при покупке облигации, который обеспечил бы инвестору в случае выполнения эмитентом своих обязательств доходность в 1.5 раза большую, чем в случае непогашения эмитентом обли­гации.

Решение. Если d- дисконт, Н - номинал, то (Н - d)есть цена разме­щения облигации. В случае, если эмитент облигацию гасит, затраты инвесто­ра составляют величину (Н - d)+180, а его доход составит Н+ 0.8*180 - (Н-d + 180) = d -36. В случае, если эмитент облигацию не гасит, затраты инве­стора будут теми же, а доход составит Н - (Н - d + 180) = d - 180. При усло­вии, что доходность в первом случае в 1,5 раза выше, а затраты равны, то d - 36=1.5*(d - 180). Тогда дисконт составит d= 468 тысяч рублей.
Пример 5.5. Бескупонная облигация "А" со сроком обращения 5 лет и бескупонная облигация "В" со сроком обращения 10 лет имеют равный но­минал. Когда до погашения облигации "А" остался 1 год, а до погашения об­лигации "В" - 3 года, рыночная стоимость облигации "А" в 4 раза превысила рыночную стоимость облигации "В". Рассчитайте величину альтернативной годовой доходности.

Решение. Если С и Н, соответственно, курсовая и номинальная
стоимости облигации "В", а r- альтернативная доходность, то по условию
задачи С = Н/(1 + r)³, а курсовая стоимость облигации "А" : 4*С = Н/(1 + r).
Приравнивая два выражения для С получаем соотношение Н/(4(1 + r)) =
Н/(1 +r)³. Отсюда следует, что 4(1+ r )= (1+r)³ , т.е. (1 +r)(4 - (1 + r)²) =0.

Следовательно, 4 -(1 + r )² = 0; (1 + r)² = 4; r = 1 =100 %.
Пример 5.6. Определить время, необходимое для увеличения первоначального капитала в три раза, используя простую и сложную процентные ставки, равные 10 % годовых.

Решение. Из соотношений S( Т) =S(0)*(1+T_nr_n); S(Т) = S(0)*(1+r_с)^Tc

Определим:

T_п=(S(T)-S(0))/(S(0)*r_n=(3-1)/0,1=20 лет

T_с=ln3/(ln(1+r_с))=1.0986/0.095=11.56 года.

Пример 5.7. Телевизор ценой 3,0 млн. рублей продается в кредит на два года под 10 % годовых (простые проценты). Погасительные платежи вно­сятся через каждый квартал. Определить размер разового погасительного платежа.

Решение. Подлежащая погашению за весь срок кредита сумма равна:

S(T) = S(0)*(1+T*r)=3*(1+2*0.1)=3.6 млн. рублей.

Разовый квартальный погасительный платеж равен: