Курсовая работа. курсач. Тики в 59 классах
 Скачать 1.6 Mb.
|
Методика использования задач с практическим содержанием на уроках математикиМетодика использования задач с практическим содержанием в 5-6 классахПри использовании задач с практическим содержанием в 5-6 классах необходимо учитывать возрастные особенности учащихся: у учащихся преобладает в этот период образная память, но затем ее значение (образной памяти) уменьшается. Тем не менее, результат запоминания обычно выше при опоре на наглядный материал. Это означает, что целесообразность использования тех или иных средств наглядности зависит от того, способствует ли деятельность, непосредственной целью которой является освоение этой наглядности, другой деятельности (основной) по овладению учащимися знаниями, ради усвоения которых и используются эти средства наглядности. Если эти две деятельности не связаны между собой, то наглядный материал бесполезен, а иногда даже может играть роль отвлекающего фактора. Рассмотрим пример, иллюстрирующий зависимость внимания от использования наглядного материала; скорость велосипедиста на 4 км/ч больше, чем скорость всадника. Через 2 ч расстояние между ними стало равным 54 км. Найти скорости велосипедиста и всадника, если первоначальное расстояние между ними равно 220 км. В качестве наглядного материала может выступать изображение велосипедиста и всадника. Какова же при этом будет деятельность учеников? Очевидно, что они будут просто рассматривать изображенные фигуры. Но эта деятельность совершенно не связана с той, которая достигает цели обучения: в данном случае выделение общего способа решения задач 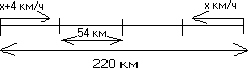 «движение навстречу друг другу». Поэтому такой наглядный материал не только не помогает осуществлению цели обучения, а мешает этому. В этом случае лучше использовать схему, изображенную ниже:в данный период развиваются вычислительные и интеллектуально- познавательные способности, увеличивается стремление к самостоятельной деятельности, вырабатывается воля достижения цели в обучении, деятельность становится осмысленной. Поэтому, чтобы у учащихся было стремление к учению, нужно идти чуть впереди их развития, но при этом опираться на принцип доступности, т.е. идти в пределах зоны ближайшего развития. Обучение (тем более решению задач с практическим содержанием, так как у каждого учащегося возникают свои трудности) должно быть личностно-ориентированным; учащимся трудно сосредоточиться на однообразной и малопривлекательной для них деятельности или на деятельности интересной, но требующей умственного напряжения, чтобы удерживать свое внимание на интеллектуальных задачах, дети должны приложить усилия, поэтому на уроке целесообразна частая смена видов деятельности; непроизвольное запоминание является более продуктивным, чем произвольное. Это становится возможным, если ученик понимает то, что он должен запомнить.[7] Темы уроков, на которых целесообразно использовать задачи с практическим содержанием
Для 6 класса, например, можно использовать следующую систему задач о вреде табакокурения по теме «Проценты»: В табачном дыме одной сигареты содержится много ядовитых веществ, разрушающих организм человека. Определите процентное содержание самых ядовитых веществ – табачного дегтя, окиси углерода, полония, - в одной сигарете, если никотина 2%; табачного дегтя в 7,5 раз больше, чем никотина; окись углерода составляет 3/5 от количества табачного дегтя; полоний составляет 2/3 от количества окиси углерода. Определите, сколько курящих детей в школе, в которой обучается 500 мальчиков и 600 девочек, если по статистике курящих мальчиков – 60%, курящих девочек – 40%. Курящие дети сокращают себе жизнь на 15%. Определите, какова продолжительность жизни нынешних курящих детей, если средняя продолжительность жизни 67 лет? При проверке состояния здоровья группы учеников школы, состоящей из 20 человек со стажем курения 3-5 лет обнаружено, что 70% из них имеет по 2 заболевания (органов дыхания и пищеварения). Остальные по одному заболеванию. Определите, сколько учащихся этой группы имеют по 2 и сколько по одному заболеванию? Средний вес новорожденного ребенка 3 кг 300гр. Если у ребенка курящий отец, то его вес будет меньше среднего на 125 гр; если курящая мать – меньше на 300 гр. Определите, сколько процентов теряет в весе новорожденный, если: а) курит папа; б) курит мама (ответ округлите до единиц) Весь мир борется с табаком. Во многих странах запрещено курение на рабочем месте. Серьезный работодатель может не принять на работу, или уволить курящего. Причину этого может объяснить следующий пример: если хороший секретарь-машинист курит, то на страницах печатного текста в 800 знаков у нее будет 4% ошибок. Сколько ошибок будет у него на страницах, где знаков в 1,5 раза больше? В теме «Проценты» необходимо показывать учащимся связь данной темы с ценами на товары и услуги. На задачи, в которых говорится о ценообразовании, в школьном курсе стали обращать внимание совсем недавно, поэтому методические подходы к их решению не очень хорошо отработаны. А между тем с ценами на товары и услуги люди встречаются каждый день, и именно школьная математика в ответе за то, чтобы эти встречи не оборачивались для людей финансовыми потерями. Примеры задач (5 класс): Яблоки в магазине стоили 3 400 рублей за 1 килограмм. Продавцы повысили цену на 5%. Какова стала стоимость яблок за 1 килограмм? Яблоки в магазине стоили 3 400 рублей за 1 килограмм. Продавцы повысили цену на 10%. На сколько меньше килограмм яблок можно купить на те же деньги? Яблоки в магазине стоили 3 400 рублей за 1 килограмм. Продавцы повысили цену на 10%, а потом снизили на 10%. Осталась ли цена прежней? Яблоки в магазине стоили 3 400 рублей за 1 килограмм. Продавцы повысили цену на 5%. На сколько надо снизить цену, чтобы цена стала прежней? В приложение 1 приведены задачи с практическим содержанием по теме «Площадь», которые целесообразно использовать при изучении данной темы. |