Курсовая работа. курсач. Тики в 59 классах

• Название: Тики в 59 классах
• Анкор: Курсовая работа
• Дата: 27.09.2021
• Размер: 1.6 Mb.
• Имя файла: курсач.docx
• Тип: Урок; #237915
• страница: 3 из 8

Классификация задач с практическим содержанием

Проблеме классификации задач с практическим содержанием в современной методической и психологической литературе уделено не очень много внимания. Задачи с практическим содержанием – это задачи практические, нестандартные. По своему функциональному назначению задачи с практическим содержанием выступают как средство обучения (направлены на формирование знаний, умений и навыков учащихся).

Существует классификация задач с практическим содержанием по величине проблемности, по числу объектов в условии задачи и связей между ними, по характеру требования, по формам решения и многие другие (схема 1).[7]

Схема 1. Классификации задач с практическим содержанием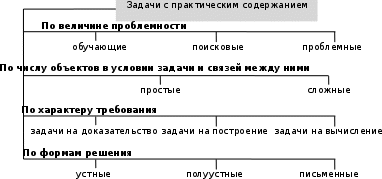




В.В. Сериков предлагает следующие типы задач с практическим содержанием.

1. 
   Задачи в контексте практико-преобразовательной деятельности человека: политехнические, технико-прикладные, проективные, экспериментально-измерительные, моделирующие, расчетно-монтажные. Сюда же могут быть отнесены задачи, связанные с различными сферами производства, видами техники, предметами и орудиями труда, материалами и технологиями, эргономикой и характеристиками деятельности человека. Пример: Строительная фирма решила построить многоквартирный жилой дом прямоугольной формы. Одним из самых важных условий при постройке нового дома всегда было правильно разметить углы. Но как получить прямой угол?
   
2. 
   Задачи, имитирующие научно-познавательную деятельность человека: проблемно-поисковые задачи, основанные на реальном и мысленном эксперименте. К этой группе мы относим также задачи, связанные с нестандартными вариантами решений ("олимпиадные"), с некорректным заданием условий, когда для решения задачи требуется предварительный поиск законов, соответствующих проблеме представленной в задаче, или самостоятельное построение адекватной модели. Ценность таких задач состоит в том, что они позволяют ученику целостно представить процесс научно-исследовательской деятельности, его эмпирические и теоретические компоненты. Примером может служить задача: есть обычный винтовой самолёт, который стоит на длинном конвейере. Самолёт
   

начинает движение, а конвейер работает по принципу комнатной беговой дорожки (человек бежит по ней, оставаясь на месте относительно пола): чем быстрее вращаются колёса на шасси самолёта, тем быстрее движется лента конвейера. Сможет ли взлететь самолёт? (трением в шасси и конвейере можно пренебречь).

3. 
   Задачи с элементами ценностно-ориентационной деятельности. В строгом смысле ценностно-ориентационная деятельность является прерогативой гуманитарных наук. Однако задачи по этим предметам тоже могут касаться некоторых фундаментальных ценностей человека. Среди таковых: проблемы безопасности жизнедеятельности и здоровья человека, вопросы экологии и охраны окружающей среды, задачи в виде мысленных экспериментов, приводящие к методологическим и мировоззренческим выводам. В таких задачах возможно представление крупных научных проблем, решавшихся в различные исторические эпохи. В современном естественнонаучном познании все чаще ученые сталкиваются с ситуацией, когда поиск истины оказывается тесно связан с нравственными проблемами. Приведем конкретный пример: после Чернобыльской аварии в окружающую среду были выброшены йод, цезий, стронций, плутоний. Активность йода равна 1,8 ЭБк, цезия на 1,715 ЭБк меньше чем йода и на 0,075 больше чем стронция, активность плутония в 600 раз меньше чем йода. Найдите суммарную активность веществ, выброшенных в окружающую среду после аварии.
   
4. 
   Задачи, связанные с коммуникационными потребностями человека. Связи человека с другими людьми имеют не только социально-психологическую, но и естественнонаучную основу. Проблемы связи, передачи сообщений, телекоммуникаций и радиокоммуникаций, физических основ радиоэлектроники и информатики; проблемы передачи вещества, энергии, информации; вопросы свойств пространства и времени, перемещений и траекторий - все это органично связано с жизнедеятельностью человека. История знает много случаев, когда интеллектуальные усилия математиков высшей квалификации в буквальном смысле слова спасали человечество. Примером такого вида задач может служить задача о перевозках по кольцевым маршрутам: На некоторых объектах находятся склады медикаментов, на других – аптеки, куда нужно доставить товар. На схеме 2 указаны запасы единиц товара на складах (со знаком +) и потребность в нем (со знаком -). Необходимо составить наиболее экономный план перевозок, чтобы удовлетворить потребности аптек, перевозя как можно меньше единиц медикаментов.
   

- 50


- 70


- 40


+ 150


- 50


- 130

+ 50
Схема 2.

- 110

Схематичный план размещения торговых точек и складов с медикаментами

5. 
   Задачи, связанные с художественной деятельностью человека: физико- химические и биологические основания эстетических феноменов природы, красота оптических эффектов, физические основы различных художественных сфер: живописи, театра, кино, телевидения, музыки. Физические и технологические основы современных эффектов в сфере искусства: голографии, мультимедиа, виртуальной реальности. Например, на рисунке 1 изображены длительности звучания нот.
   

Рис. 1 – Длительности звучания нот

Необходимо посчитать в произведении, изображенном на рисунке 2, длительность звучания одного такта и определите длительность звучания данного произведения.



Русская народная песня “Во поле береза стояла”

6. 
   Спорт и физические возможности человека. Спортсмен пробегает за первый день 2 км, каждый последующий день он увеличивает норму пробега на 50 %. Определите через сколько дней норма пробега может стать более 50 км.
   
7. 
   Физика, химия, геометрия, дизайн в обеспечении эстетических свойств жилья и среды обитания человека. Примером может служить задача о ремонте: у вас есть коробка с декоративной плиткой. На первый взгляд плитки должно было хватить на бордюр в двух
   

комнатах. Но вдруг у вас возникла проблема. Когда вы попробовали сделать бордюр шириной в две плитки, одна плитка оказалась лишней. То же самое произошло и тогда, когда вы попытались уложить полоски шириной в три, четыре, пять, шесть плиток. И только когда вы положили по семь плиток в каждый угол, все сошлось. Плиток как раз хватило и не осталось одной лишней. Какое наименьшее количество плиток могло лежать в найденной коробке? [7]

К задачам с практическим содержанием естественно наряду с общими требованиями к математическим задачам предъявить и следующие дополнительные:

1. 
   задача должна давать достаточно пищи для мыслительной деятельности, иметь познавательную ценность;
   
2. 
   необходимо чтобы условие задачи было четко сформулировано, а содержание нематематического материала доступно пониманию школьников;
   
3. 
   в условии задачи должны быть реальными описываемая ситуация, числовые значения данных, постановка вопроса и полученный результат.
   

Задачи практического характера целесообразно использовать в процессе обучения для раскрытия многообразия применений математики в жизни, своеобразия отражения ею реального мира и достижения таких дидактических целей как:

1. 
   мотивация введения новых математических понятий и методов;
   
2. 
   иллюстрация учебного материала;
   
3. 
   закрепление и углубление знаний по предмету;
   
4. 
   формирование практических умений и навыков.[5]
   

Задачи с практическим содержанием можно применять на различных этапах урока. Использование задач как средства мотивации знаний неоднозначно. С одной стороны, такие задачи своим интегрированным содержанием, необходимостью использования сформированных приемов умственных действий, опорой на дополнительный материал, добытый в ходе самообразования, в случае умелой организации учебной работы и своевременного, программно согласованного введения задач в учебный процесс со стороны учителя, способствуют развитию положительной мотивации учения. С другой стороны, без учета этих особенностей решение задач с практическим содержанием затрудняет развитие положительной мотивации. Чтобы не возникало таких трудностей, задачи с практическим содержанием должны быть подобраны так, чтобы их постановка привела к необходимости приобретения учащимися новых знаний по математике, а приобретенные под влиянием этой необходимости знания позволили решить не только поставленную задачу с практическим содержанием, но и ряд других задач прикладного характера. Для создания проблемной ситуации можно

использовать и отдельные фрагменты задач с практическим содержанием, а задачи в целом рассмотреть на уроках обобщения и систематизации знаний. Использование задач проблемного характера обеспечивает более сознательное овладение математической теорией, учит школьников самостоятельному выполнению учебных заданий, приемам поиска, исследования и доказательства, основным мыслительным операциям. [5]

Нами было определено, что же называется задачей с практическим содержанием. Существует еще одно близкое по значению понятие - это понятие прикладной задачи. Что же называется прикладной задачей? В педагогической литературе понятие прикладной задачи трактуется по-разному. Одни исследователи прикладной называют задачу, требующую перевода с естественного языка на математический. Другие исследователи считают, что прикладные задачи должны быть по своей постановке и методам решения более близкой к задачам, возникающим на практике. Так, М.В. Крутихина под прикладной задачей понимает сюжетную задачу, сформулированную, как правило, в виде задачи- проблемы и удовлетворяющую следующим требованиям:

1. 
   вопрос должен быть поставлен в таком виде, в каком он обычно ставится на практике (решение имеет практическую значимость);
   
2. 
   искомые и данные величины (если они заданы) должны быть реальными, взятыми из практики».
   

Н.А. Терешин в своей книге «Прикладная направленность школьного курса математики» дает следующее определение: «Прикладная задача – это задача, поставленная вне математики и решаемая математическими средствами».

Особенностью прикладных задач является то, что при их решении наряду с логикой используются также и правдоподобные рассуждения, утверждения, справедливые в типичных случаях, доводы, основанные на аналогии, на численном или физическом эксперименте, то есть такие, которые неприемлемы в чистой (теоретической) математике, или служащие в ней лишь способом наведения учащихся на доказательство. Таковыми служат:

1. 
   рассуждения по аналогии;
   
2. 
   применение понятий вне рамок их первоначального определения;
   
3. 
   применение актуальной (практической) бесконечности, т. е. трактовка бесконечно малых и бесконечно больших величин как постоянных, но имеющих другой порядок, чем остальные величины;
   
4. 
   использование результатов приближенного решения при отсутствии точного решения. [5]
   

Д.В.):

К прикладной задаче следует предъявлять следующие требования (Ожерельев

1. 
   в содержании прикладных задач должны отражаться математические и
   

нематематические проблемы и их взаимная связь;

2. 
   задачи должны соответствовать программе курса, вводится в процесс обучения как необходимый компонент, служить достижению цели обучения;
   
3. 
   вводимые в задачу понятия, термины должны быть доступными для учащихся, содержание и требование задач должны “сближаться” с реальной действительностью;
   
4. 
   способы и методы решения задач должны быть приближены к практическим приемам и методам;
   
5. 
   прикладная часть задач не должна покрывать ее математическую сущность.
   

Для реализации прикладной направленности в обучении математике существенное значение имеет использование в преподавании различных форм организации учебного процесса.

Чем отличаются эти два понятия? Надо сказать, что задача с практическим содержанием – это математическая задача, которая раскрывает межпредметные связи и только знакомит нас со сферами человеческой деятельности, в которых она может использоваться Прикладная задача – это все-таки задача не математическая. Она может быть поставлена в любой сфере человеческой деятельности, это может быть как инженерия, так и текстильное производство. Но так как и задача с практическим содержанием, прикладная задача решается математическими средствами, опираясь при этом на математические правила и формулы.[3]