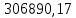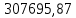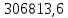Ф для Нф РГР 1 (1). Титульный лист, графики и таблицы обязательно оформляются на компьютере
 Скачать 222 Kb.
|
|
Задание 2 Денежные средства в размере P тенге размещаются в виде тенгового депозита на один год с ежемесячным начислением процентов с капитализацией. Номинальная годовая ставка начисления процентов равна начала операции – Дата 1, год 2021,  . Операция прерывается раньше срока. Дата прерывания операции – Дата 2, год 2021.Определить начисляемые проценты и наращенные суммы, если согласно договору при досрочном расторжении должна быть применена схема: 1) дробного процента; 2) смешанного процента; 3) без начисления процентов за неполный последний период начисления. При расчетах неполного месяца считать, что в полном месяце 30 дней. Основные результаты решения оформить в виде таблицы: Данные для расчетов в задании 2: такие же, как и для задания 1.
Данные для решения Таблица 1 и таблица 2:   Пример решения: Денежные средства в размере P = 300 000 тенге размещаются в виде тенгового депозита на один год с ежемесячным начислением процентов с капитализацией. Номинальная годовая ставка начисления процентов равна i = 4,5%. Дата начала операции – 31 марта 2021 года. Операция прерывается раньше срока. Дата прерывания операции – 23 октября 2021 года. Определить начисляемые проценты и наращенные суммы, если согласно договору при досрочном расторжении должна быть применена схема: 1) дробного процента; 2) смешанного процента; 3) без начисления процентов за неполный последний период начисления. При расчетах неполного месяца считать, что в полном месяце 30 дней. Решение: Наращение по смешанному методу производится по формуле: 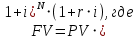 PV – сумма вложенных средств; FV – наращенная сумма; i – процентная ставка, отнесенная к расчетному периоду времени (год, квартал, месяц и т.п.);  – продолжительность времени между началом и концом финансовой операции; N – число целых расчетных периодов между началом и концом операции; r – оставшийся неполный интервал времени между началом и концом операции, выраженный в долях расчетного периода, всегда  .Определим полное число месяцев между датами финансовой операции. С 31 марта по 23 октября пройдет 6 полных месяцев. Найдем число дней между 30 сентября и 23 октября. Между этими датами 23 дня. Значит  .Заметим, что начисления процентов происходят ежемесячно, а в договоре зафиксирована годовая процентная ставка  . Тогда ставка, отнесенная к расчетному периоду времени (месяцу) будет равна 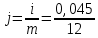 , т.к. в году 12 месяцев.Наращенная сумма по формуле смешанного процента будет равна: 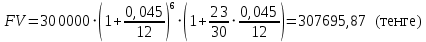 Расчет суммы начисленных процентов:  Наращение по схеме без начисления процентов за неполный последний период начисления. При этой схеме наращение за все полные периоды проводится по схеме сложных процентов, а за оставшийся неполный период проценты не начисляются. Расчет наращенной суммы:  Расчет суммы начисленных процентов:  Наращение по схеме с дробным периодом начисления. При этой схеме наращение за все периоды проводится по схеме сложных процентов, то есть в формуле сложного процента появляется дробный показатель степени. 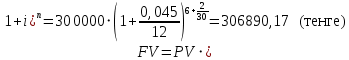 Расчет суммы начисленных процентов:  Таблица 2 Основные результаты решения Задания 2
Задание 3 У фирмы, предоставляющей услуги экспресс-кредитования, есть две возможности (схемы) кратковременного размещения средств: СХЕМА 1 – выдать денежные средства в размере P1 тенге на M1 месяцев и получить в конце операции Q1 тенге; СХЕМА 2 – выдать денежные средства в размере P2 тенге на M 2 месяцев и получить в конце операции Q2 тенге. Определить, какая из схем наиболее выгодна для фирмы, если операции оцениваются по правилу простого процента. Вывод обосновать. Основные результаты решения оформить в виде вывода, примерно такого содержания: Вывод: фирме выгоднее предоставить денежные средства по схеме (1 или 2), потому что (краткое обоснование с приведением сравнения необходимых параметров). Данные для расчетов в задании 3:
Пример решения: (две последние цифры 03) У банка имеется возможность кратковременного размещения средств по двум схемам: СХЕМА 1 – выдать денежные средства в размере P1 = 650 000 тенге на M1 = 9месяцев и получить в конце операции Q1 = 1 100 000тенге; СХЕМА 2 – выдать денежные средства в размере P2= 200 000тенге на M2 = 3 месяца и получить в конце операции Q2 = 250 000 тенге. Определить, какая из схем наиболее выгодна для банка, если операции оцениваются по правилу простого процента. Вывод обосновать. Решение: Сравнение краткосрочных финансовых операций проводится на основе сравнения эффективной процентной ставки для схемы простого процента. 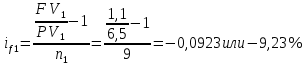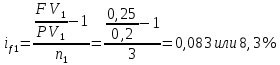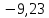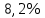Для схемы 1:  Для схемы 2:  Таким образом, эффективная ставка первой операции  в месяц, а второй  в месяц. Для заемщика операция тем выгоднее, чем ниже процент, для банка, выдающего кредит – наоборот. Значит для банка выгоднее 2 вариант операции. Задание 4 В банк сделан вклад в размере P тенге сроком на n лет под i % годовых. Проценты начисляются по схеме сложного процента. Определить, какая сумма будет возвращена в конце срока операции, если проценты начисляются и капитализируются: а) раз в год; б) раз в полгода; в) раз в квартал; г) раз в два месяца; д) раз в месяц; е) два раза в месяц; ж) раз в неделю (считать, что в году ровно 53 недели); з) раз в день (считать, что в году 365 дней); и) непрерывно. Для всех указанных случаев определить эффективную годовую процентную ставку (в этом задании – с точностью до тысячной доли процента). Построить график зависимости эффективной процентной ставки от числа начислений процентов в год. (Рекомендуется использовать логарифмическую шкалу для оси отображения числа начислений процентов в год. Непрерывное начисление на график не заносить). Основные результаты решения оформить в виде таблицы:
Данные для расчетов в задании 4: Таблица 1 и таблица 2: Пример решения:две последние цифры пропуска АУЭС-03.   Решение: а) раз в год Проценты начисляются и капитализируются раз в год, тогда  Наращенная сумма: 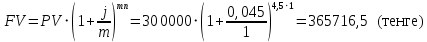 Эффективная ставка:  б) раз в полгода Число периодов начислений в год: m = 2 Наращенная сумма:  Эффективная ставка:  |
