Ф для Нф РГР 1 (1). Титульный лист, графики и таблицы обязательно оформляются на компьютере
 Скачать 222 Kb. Скачать 222 Kb.
|
|
в) раз в квартал Число периодов начислений в год: m = 4 Наращенная сумма: 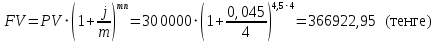 Эффективная ставка: 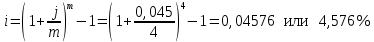 г) раз в два месяца Число периодов начислений в год: 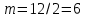 Наращенная сумма: 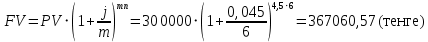 Эффективная ставка: 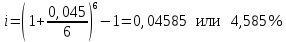 д) раз в месяц Число периодов начислений в год: m = 12 Наращенная сумма: 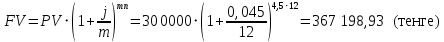 Эффективная ставка: 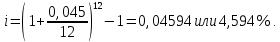 е) два раза в месяц Число периодов начислений в год: m = 24 Наращенная сумма: 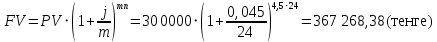 Эффективная ставка: 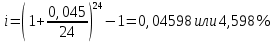 ж) раз в неделю (считать, что в году ровно 53 недели) Число периодов начислений в год: m = 53 Наращенная сумма: 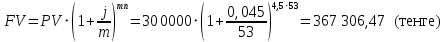 Эффективная ставка: 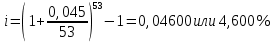 з) раз в день (считать, что в году 365 дней) Число периодов начислений в год: m = 365 Наращенная сумма: 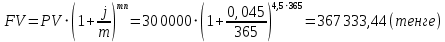 Эффективная ставка: 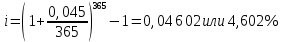 и) непрерывно Наращенная сумма: 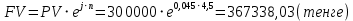 Эффективная ставка: 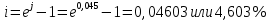 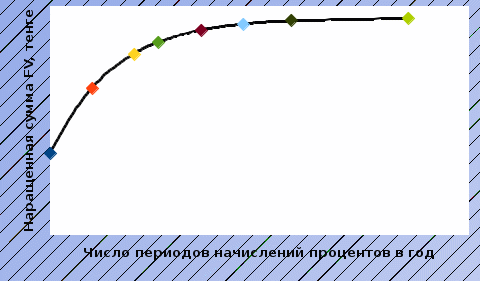 Рисунок 1 – График зависимости наращенной суммы от числа периодов начислений в год (логарифмическая шкала) Как видно из графика, существенные изменения наращенной суммы происходят примерно до ежемесячных начислений ( 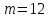 ). При более частых начислениях наращенная сумма возрастает уже слабо. ). При более частых начислениях наращенная сумма возрастает уже слабо.Таблица 3 Основные результаты решения Задания 4
Задание 5 В банк сделан вклад в размере P тенге сроком на n лет под i % годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются так, как указано в таблице с данными к заданию. За указанный период времени среднегодовой уровень инфляции составил 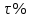 . .Определить: 1) реальную наращенную сумму за указанный период времени; 2) реальную годовую процентную ставку; 3) компенсирующую годовую процентную ставку указанной операции, соответствующую данному уровню инфляции; 4) обеспечивающую годовую процентную ставку указанной операции, для реальной доходности 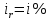 в год при данном уровне инфляции. в год при данном уровне инфляции.Основные результаты решения оформить в виде таблицы:
Данные для расчетов в задании 5: Таблица 1 и таблица 2:   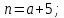 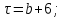 Начисление процентов
Пример решения: Допустим, две последние цифры пропуска АУЭС - 95. 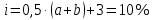 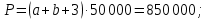 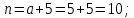 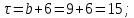 Проценты начисляются раз в месяц. В банк сделан вклад в размере P = 850 000 тенге сроком на 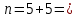 10 лет под 10 лет под  = 10,0% годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются два раза в месяц. = 10,0% годовых. Проценты начисляются по схеме сложного процента. Проценты начисляются два раза в месяц.За указанный период времени среднегодовой уровень инфляции составил 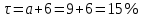 . .Определить: 1) реальную наращенную сумму за указанный период времени; 2) реальную годовую процентную ставку; 3) компенсирующую годовую процентную ставку указанной операции, соответствующую данному уровню инфляции; 4) обеспечивающую годовую процентную ставку указанной операции, для реальной доходности 10,0% в год при данном уровне инфляции. Решение: Определим сначала сумму вклада к концу срока наращения (начисления раз в полгода, m = 2): 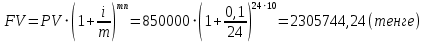 Рассчитываем реальную наращенную сумму за указанный период времени: 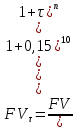 Рассчитываем реальную годовую процентную ставку: 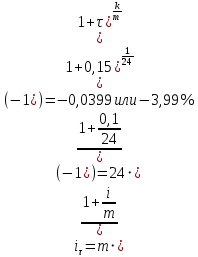 Так как реальная наращенная сумма (569 944,71 тенге) оказалась ниже суммы вклада (850 000 тенге), то и реальная процентная ставка оказалась отрицательной. Процесс обесценивания денег за счет инфляционных процессов происходит интенсивнее, чем начисление процентов по вкладу. Определим обеспечивающую годовую процентную ставку указанной операции, для реальной доходности 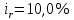 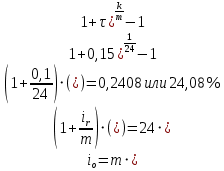 Определим компенсирующую ставку: 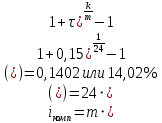 Таблица 4 Основные результаты решения Задания 5
Задание 6 У предпринимателя есть ценная бумага, гарантирующая выплату по ней в размере P тенге через n лет. Предприниматель, желая получить деньги прямо сейчас, переуступает это обязательство банку. Банк согласен принять данную ценную бумагу с дисконтом i % годовых. Определить, какая сумма будет выплачена предпринимателю, если дисконтирование будет осуществлено по следующим схемам: а) по правилу математического дисконтирования с простым процентом; б) по правилу математического дисконтирования со сложным процентом; в) по правилу банковского учета с простым процентом; г) по правилу банковского учета со сложным процентом. Для вариантов, в которых получатся отрицательные значения, прокомментировать их. Основные результаты решения оформить в виде таблицы:
Данные для расчетов в задании 6: 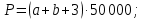 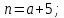 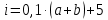 Пример решения: 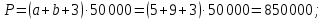 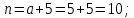 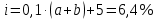 У предпринимателя есть ценная бумага, гарантирующая выплату по ней в размере P = 850 000 тенге через n = 10 лет. Предприниматель, желая получить деньги прямо сейчас, переуступает это обязательство банку. Банк согласен принять данную ценную бумагу с дисконтом i= 6,4% годовых. Определить, какая сумма будет выплачена предпринимателю, если дисконтирование будет осуществлено по следующим схемам: а) по правилу математического дисконтирования с простым процентом; б) по правилу математического дисконтирования со сложным процентом; в) по правилу банковского учета с простым процентом; г) по правилу банковского учета со сложным процентом. Решение: а) Находим дисконтированную сумму по правилу математического дисконтирования с простым процентом 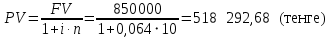 б) Находим дисконтированную сумму по правилу математического дисконтирования со сложным процентом 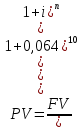 в) Находим дисконтированную сумму по правилу банковского учета с простым процентом 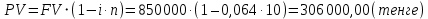 г) Находим дисконтированную сумму по правилу банковского учета со сложным процентом 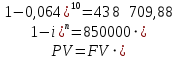 (тенге) (тенге)Результаты расчетов представлены в таблице 5: Таблица 5 Основные результаты решения Задания 6
Задание 7 У предпринимателя есть три варианта долгосрочного вложения средств: ВАРИАНТ 1 – вложить денежные средства в размере  тенге на тенге на  лет в банк под лет в банк под  % годовых с ежемесячным начислением процентов; % годовых с ежемесячным начислением процентов;ВАРИАНТ 2 – вложить средства в размере 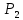 тенге на тенге на  лет в проект, который принесет в конце срока не облагаемый налогом доход лет в проект, который принесет в конце срока не облагаемый налогом доход  тенге; тенге;ВАРИАНТ 3 – вложить денежные средства в размере  тенге на тенге на 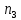 лет в бизнес, который принесет в конце срока доход лет в бизнес, который принесет в конце срока доход 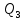 тенге, но с разницы между доходом и вкладом нужно будет заплатить налог тенге, но с разницы между доходом и вкладом нужно будет заплатить налог %. %.Определить, какой из вариантов вложения средств наиболее выгоден для предпринимателя, если операции оцениваются по правилу сложного процента. Вывод обосновать. Основные результаты решения оформить в виде вывода, примерно такого содержания: Вывод: предпринимателю выгоднее выбрать (1 или 2 или 3) вариант вложения денежных средств, потому что (краткое обоснование с приведением сравнения необходимых параметров). |
