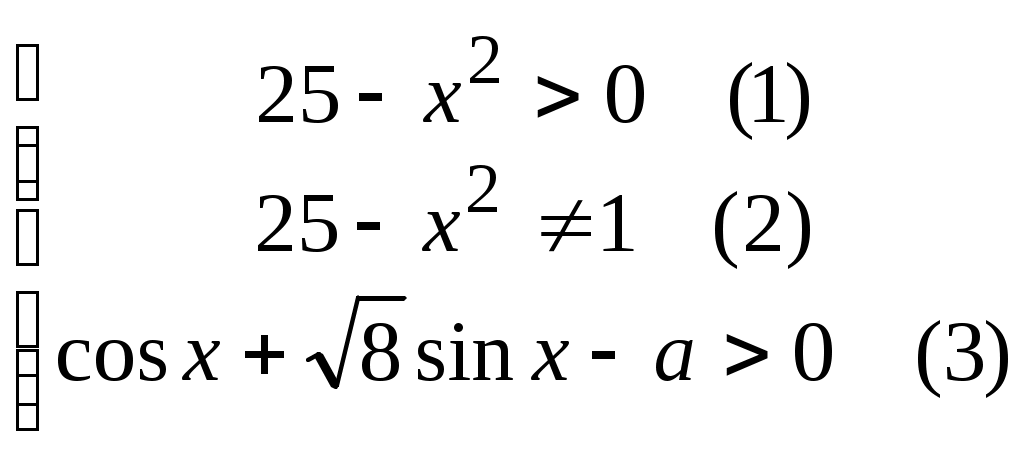Пример 77. Найти все значения «р», при которых уравнение 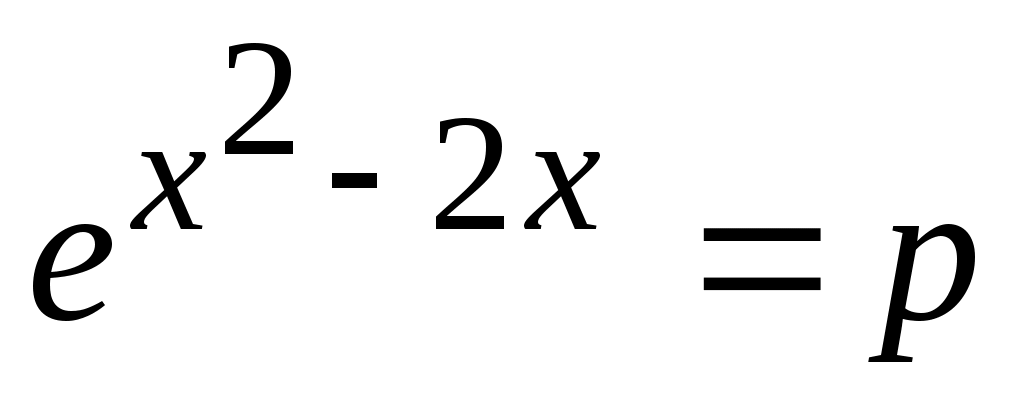 имеет одно решение. имеет одно решение.
Ответ: 1е.
Функция 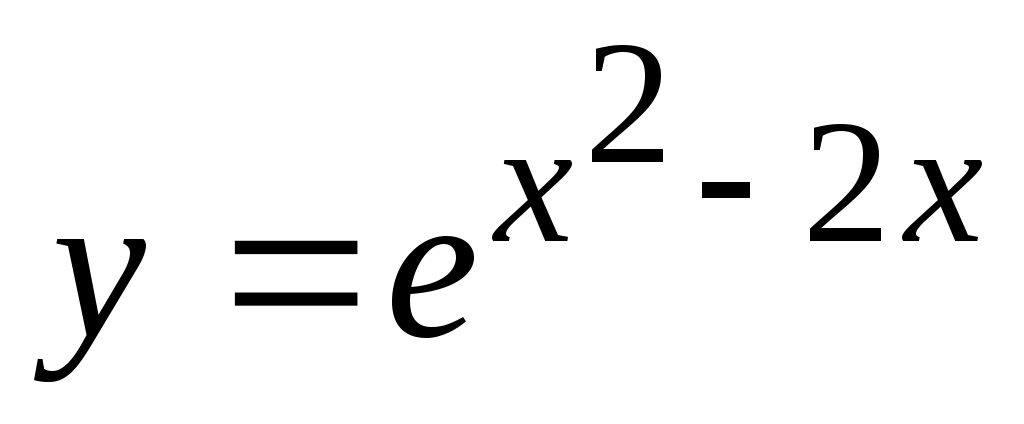 >0 при любых значениях >0 при любых значениях  и имеет наименьшее значение при условии и имеет наименьшее значение при условии  . Найдем решение данного уравнения (для проверки: . Найдем решение данного уравнения (для проверки:  =1); =1); 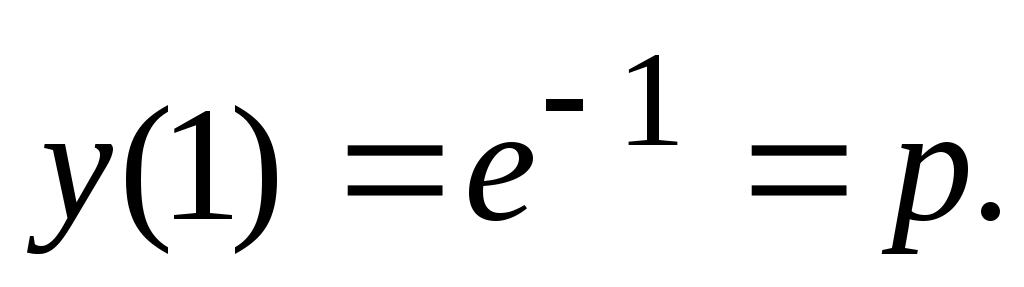
Пример 78. Найти все значения «р», при которых уравнение
 имеет одно решение. Ответ: 14. имеет одно решение. Ответ: 14.
В уравнении  необходимо убрать знак модуля при условии: необходимо убрать знак модуля при условии: 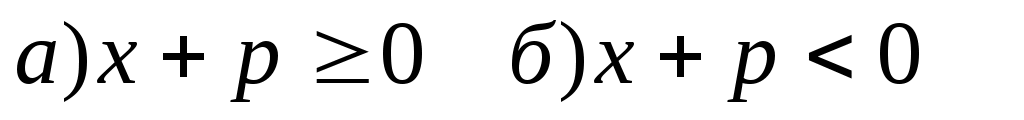 и решать уравнения и решать уравнения 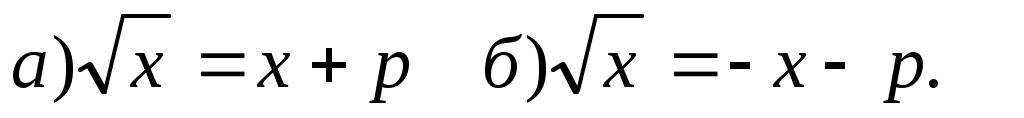
Если уравнение записать в виде 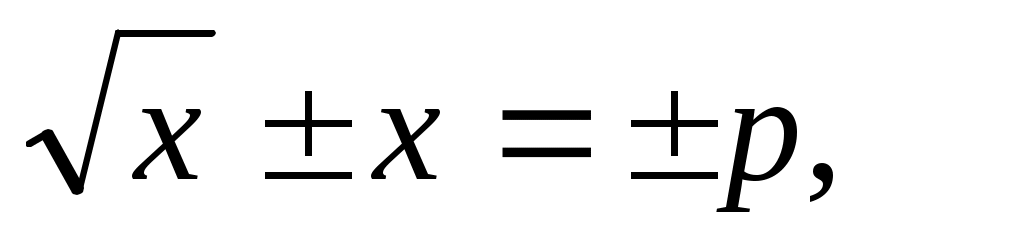 то единственное решение проще найти графически, заменяя то единственное решение проще найти графически, заменяя 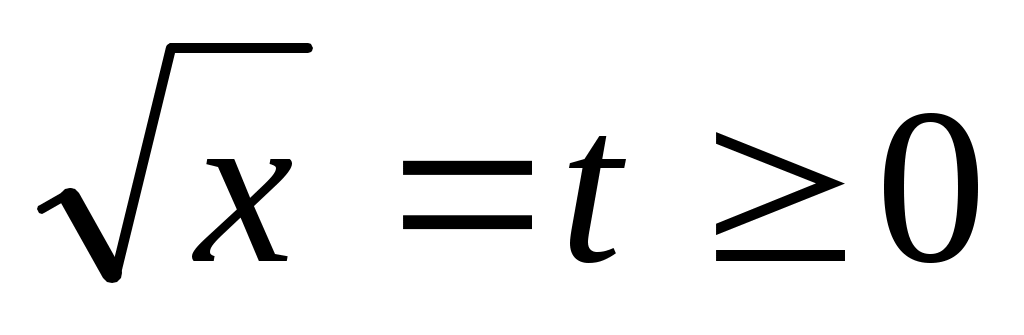 и получая уравнение и получая уравнение  . Необходимо из двух уравнений выбрать одно. Левая часть уравнения представляет собой параболу с вершиной . Необходимо из двух уравнений выбрать одно. Левая часть уравнения представляет собой параболу с вершиной 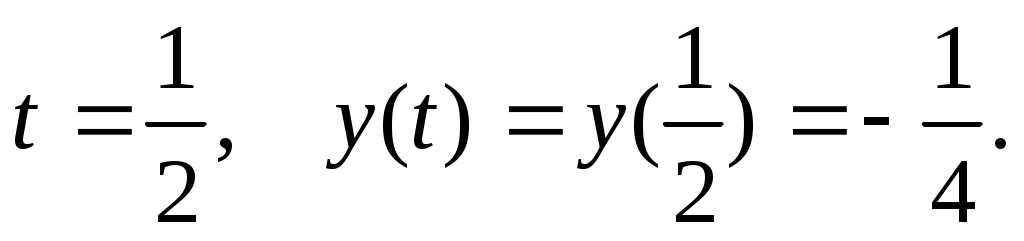 Условие Условие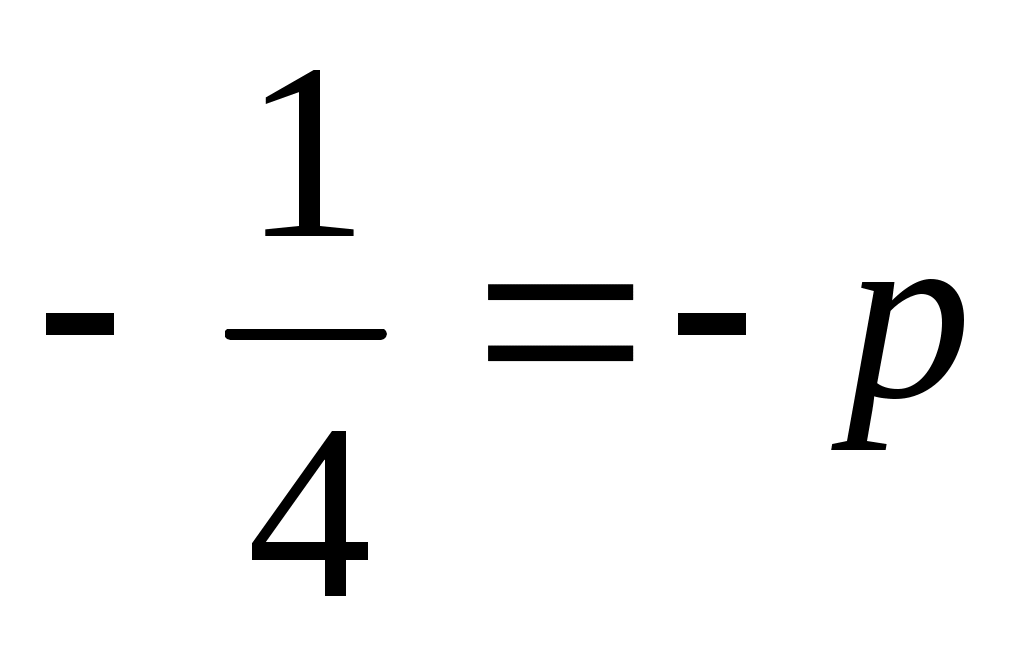 определяет значение параметра: определяет значение параметра:  . .
Пример 79. Найти все значения «а», при которых наименьшее
решение неравенства 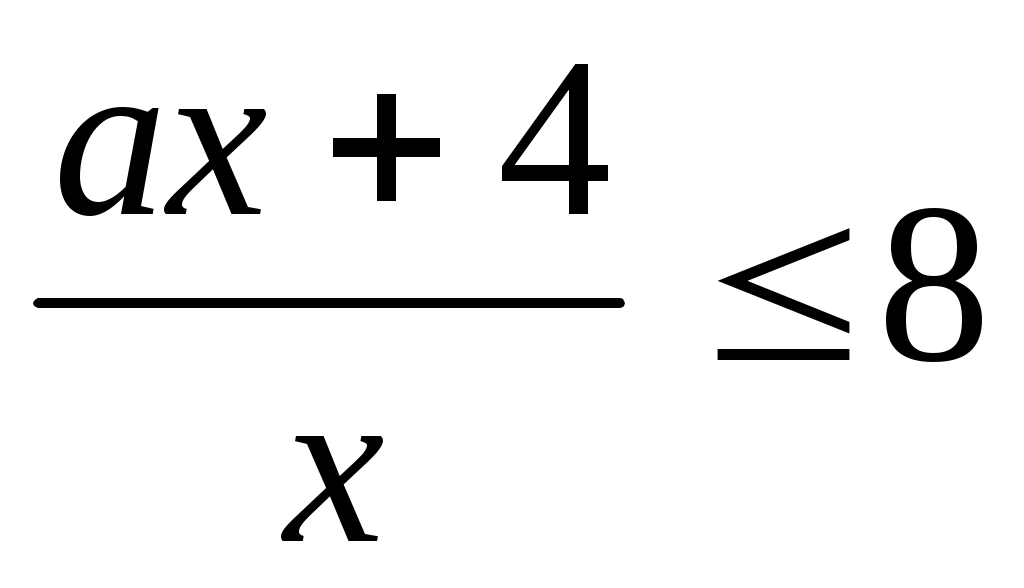 равно –1. равно –1.
Ответ: 12.
Преобразуем неравенство 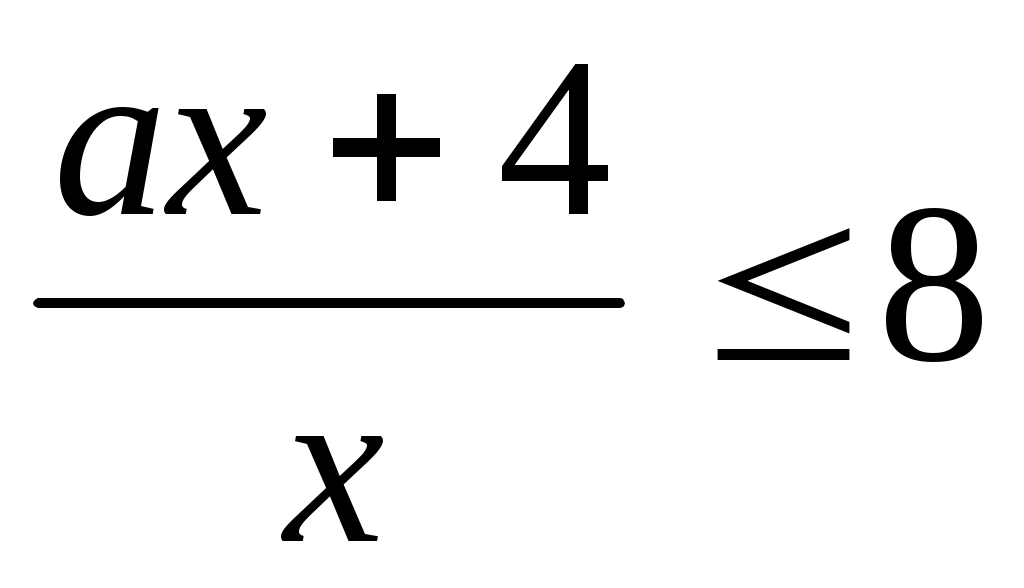 к виду к виду 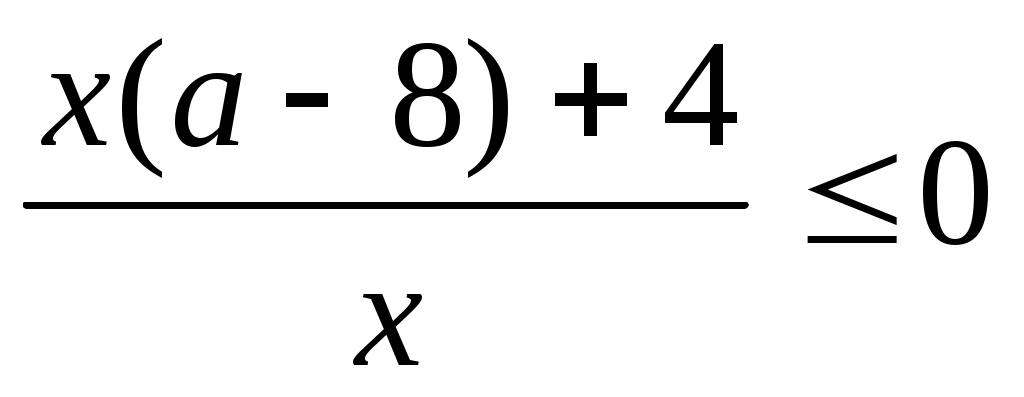 , ,
и будем его решать методом интервалов с нулевыми точками
 . Значение . Значение  может быть как больше нуля, так и меньше. Необходимо рассмотреть оба варианта и получить решение неравенства. По условию задачи, наименьшее решение должно быть равно (-1). В одном из вариантов (8- может быть как больше нуля, так и меньше. Необходимо рассмотреть оба варианта и получить решение неравенства. По условию задачи, наименьшее решение должно быть равно (-1). В одном из вариантов (8-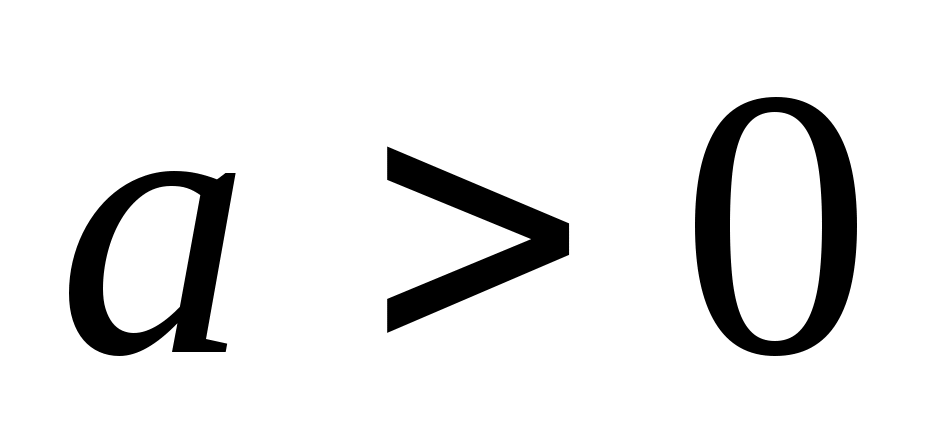 ) такого решения быть не может. ) такого решения быть не может.
Пример 80. При каких значениях «а» уравнение
имеет единственное решение?
Ответ: 4 (-;0).
Преобразуем  к виду к виду 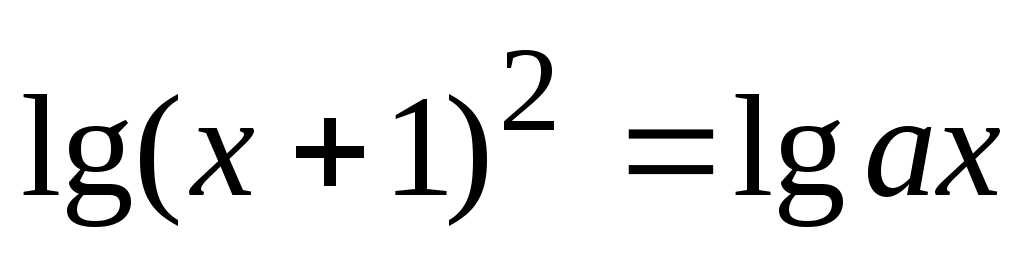 и перейдем к решению уравнения и перейдем к решению уравнения 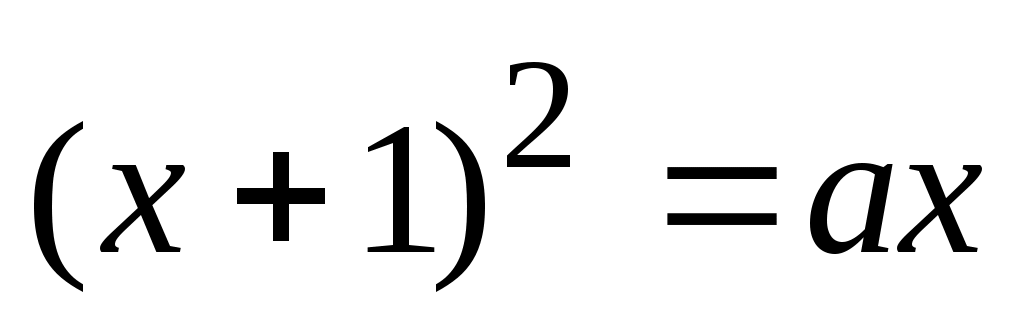 при условии, что при условии, что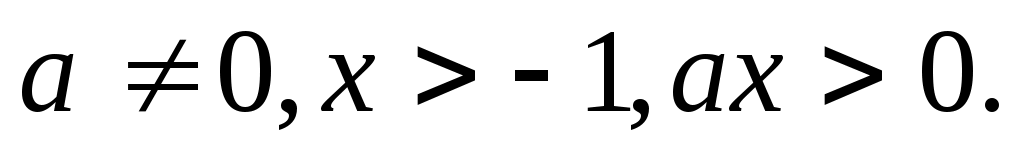
Единственное решение возможно в двух случаях: 1)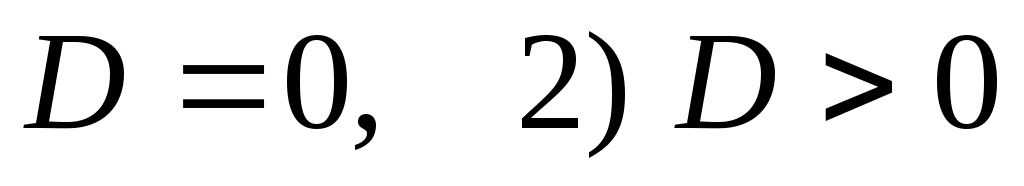 , но один из корней уравнения , но один из корней уравнения 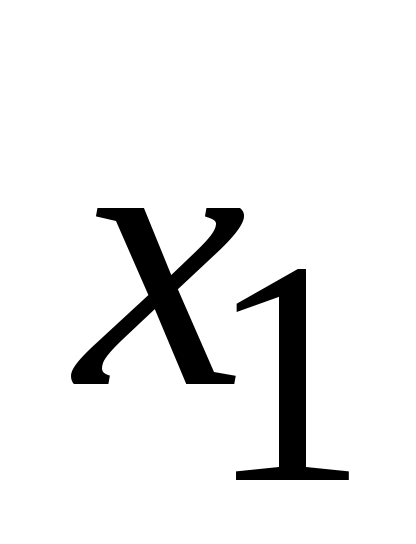 или или 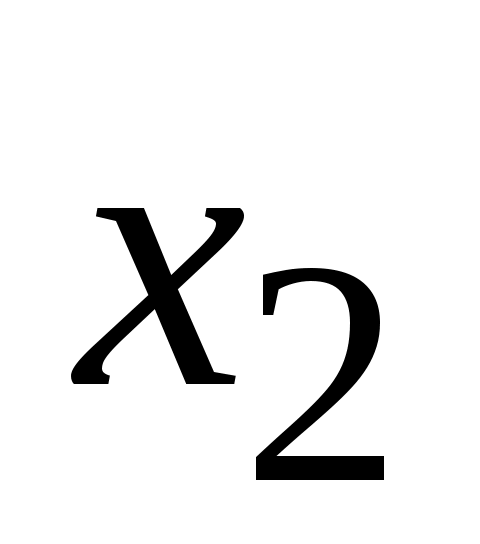 не удовлетворяют условию задачи. Для случая не удовлетворяют условию задачи. Для случая 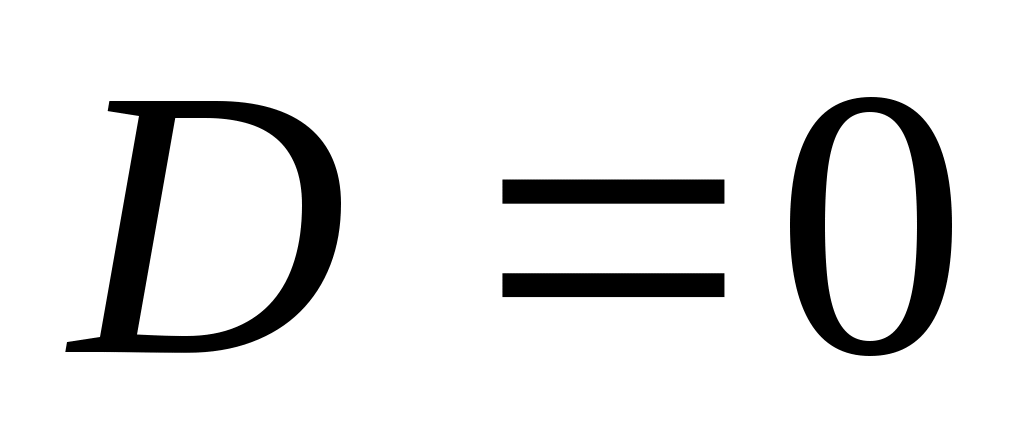 получаем решение получаем решение  , при , при 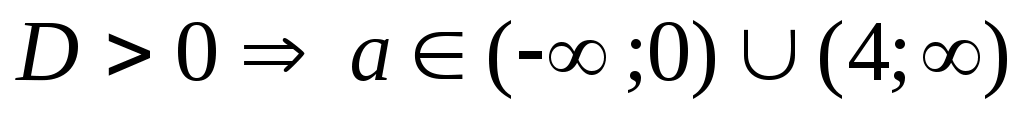 только в случае только в случае 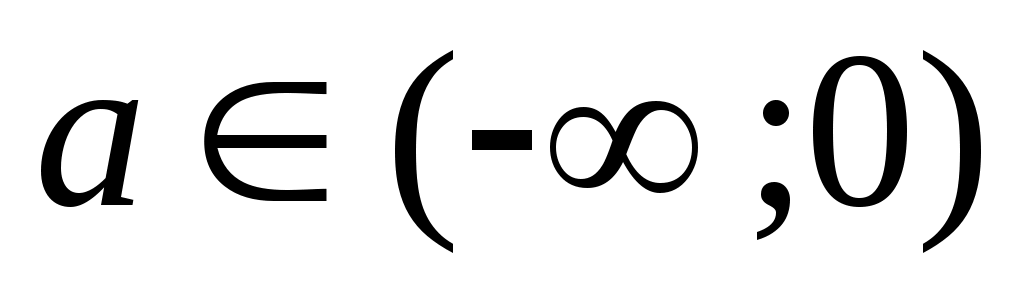 решение будет единственным. решение будет единственным.
Пример 81. При каких значениях «а» уравнение 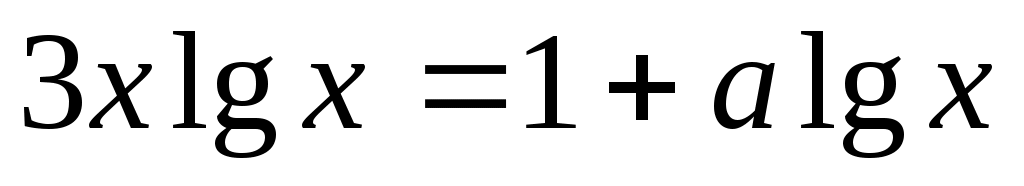
имеет единственное решение?
Ответ: а0.
Преобразуем 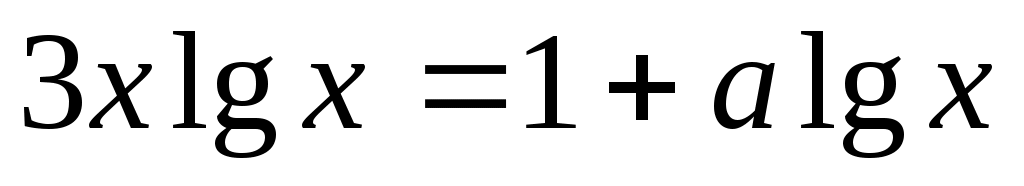 к виду к виду 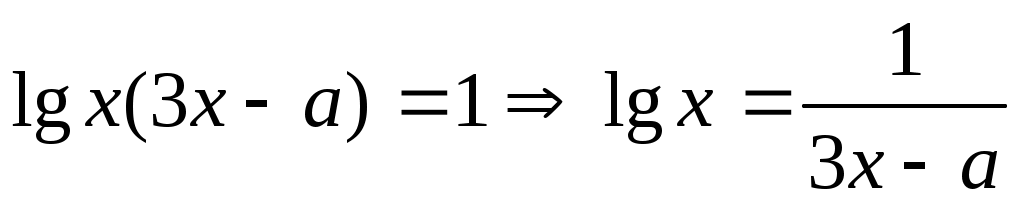 . Решение уравнения необходимо выполнить графически, то есть построить известные функции . Решение уравнения необходимо выполнить графически, то есть построить известные функции 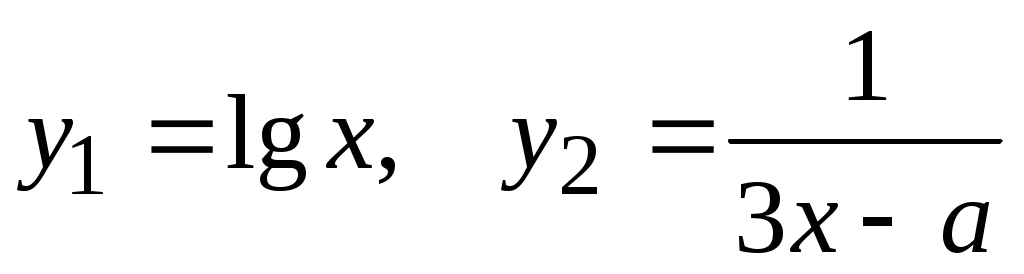 и подобрать значение и подобрать значение  так, чтобы точка пересечения графиков была единственной. так, чтобы точка пересечения графиков была единственной.
Пример 82. При каких значениях «а» функция
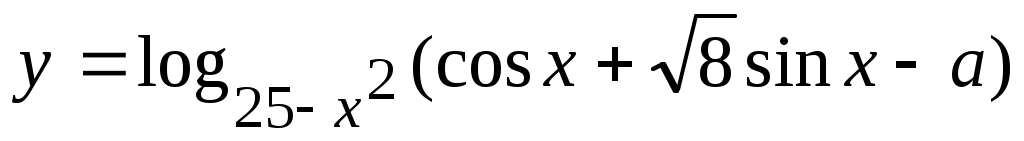 определена при любых определена при любых
значениях «х»?
Область определения функции 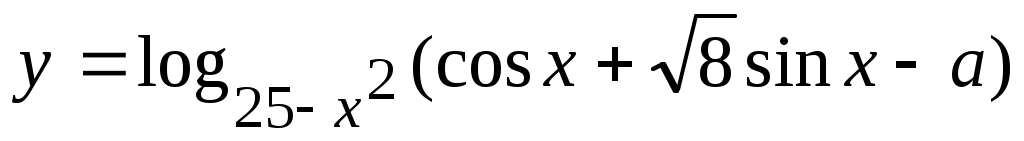 находится при выполнении условий находится при выполнении условий 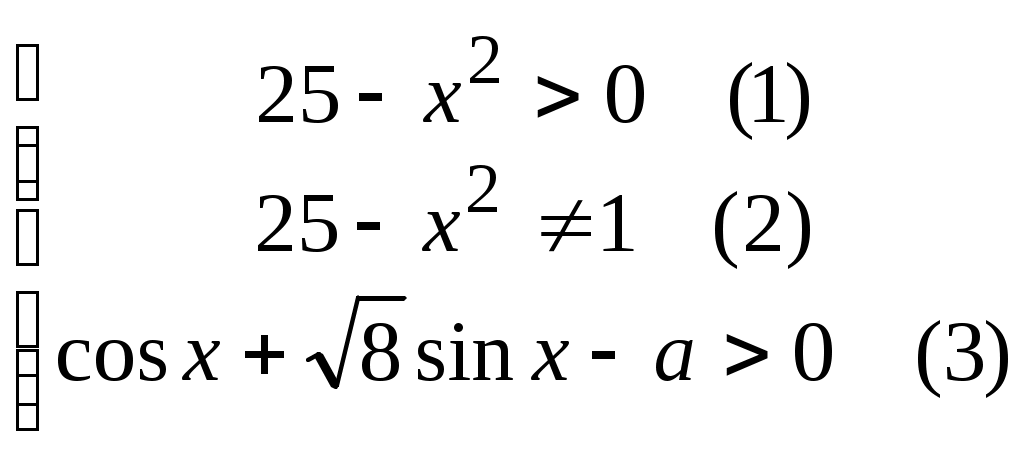
Решение (1) и (2) определяет 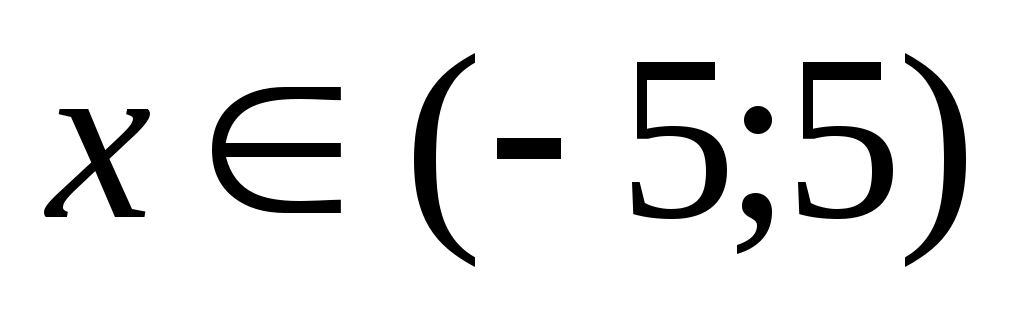 за исключением значений за исключением значений
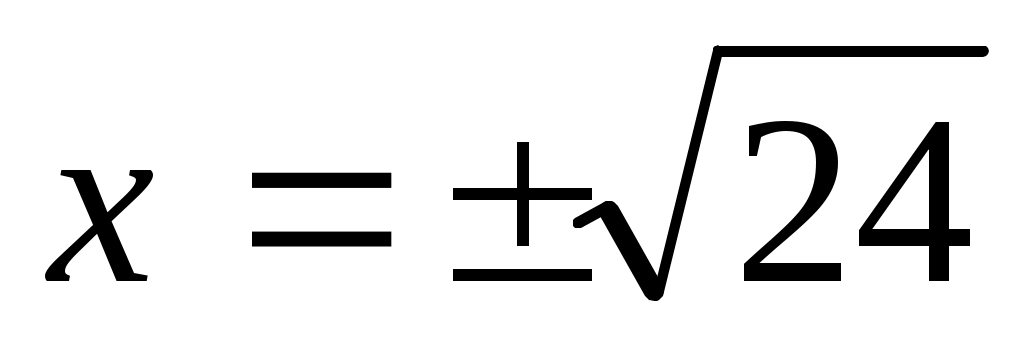 . Решение (3) удобнее находить в виде . Решение (3) удобнее находить в виде 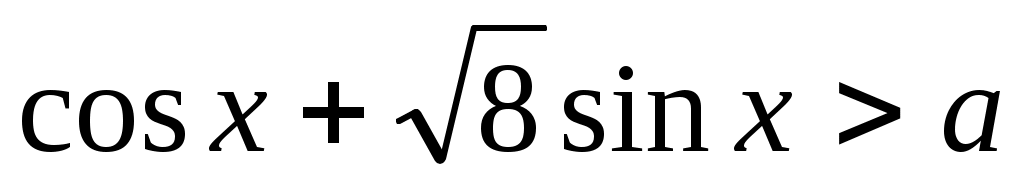 , обозначая , обозначая 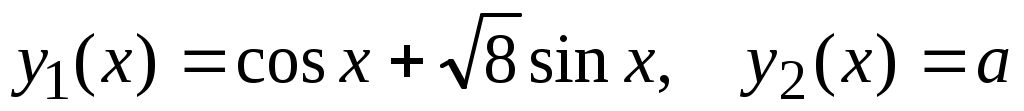 . Тогда . Тогда 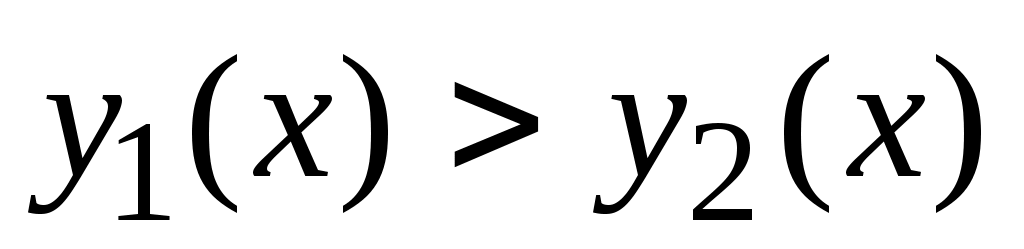 . Необходимо определить минимум функции . Необходимо определить минимум функции 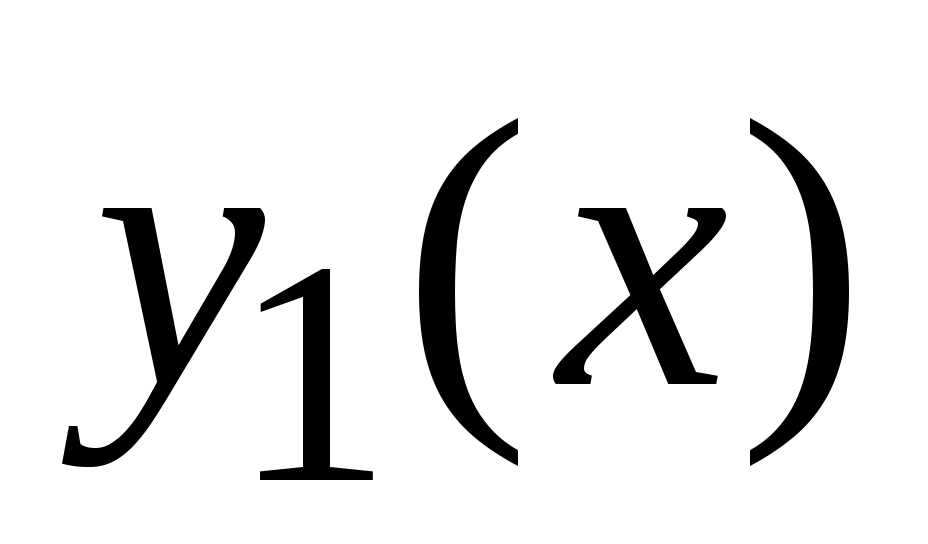 , используя равенство нулю ее производной: , используя равенство нулю ее производной: 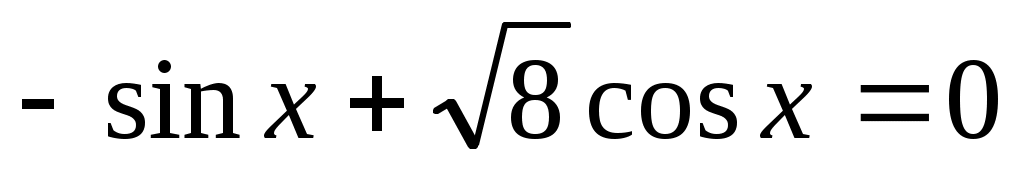 . Точкой минимума является точка с координатами . Точкой минимума является точка с координатами 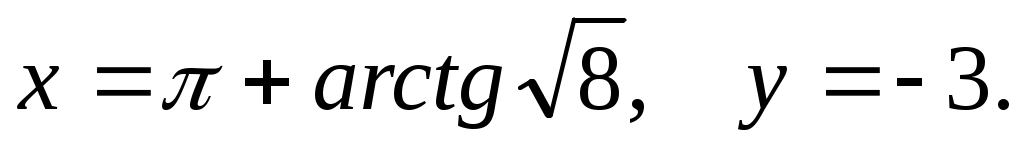
Выполнение условия  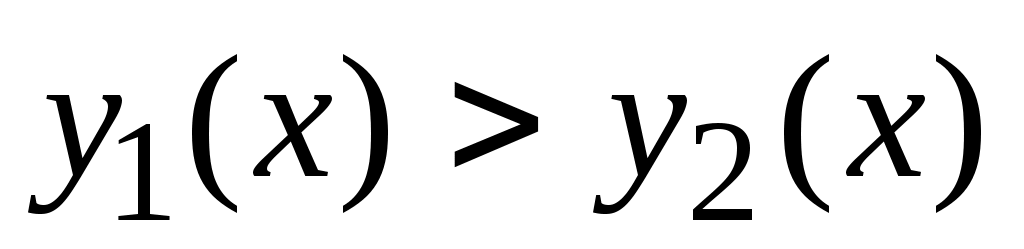 достигается при значении достигается при значении
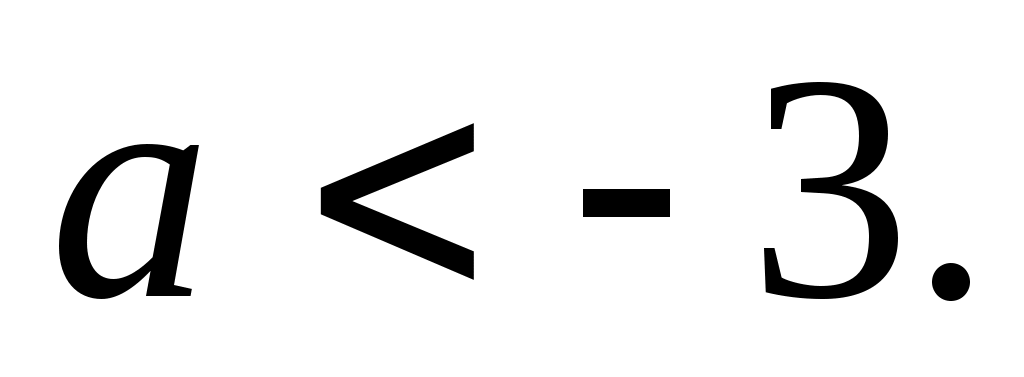 С учетом (1) и (2) решением задачи являются значения С учетом (1) и (2) решением задачи являются значения
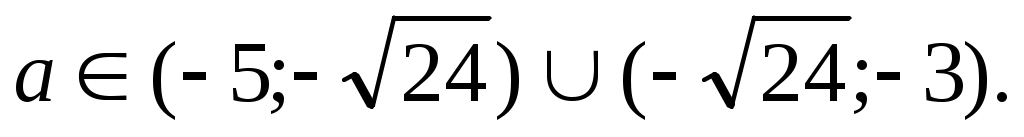 |
 Скачать 1.98 Mb.
Скачать 1.98 Mb.