Задачи. томский политехнический университет

• Название: томский политехнический университет
• Анкор: Задачи
• Дата: 23.03.2023
• Размер: 1.98 Mb.
• Имя файла: zadachi.doc
• Тип: Сборник задач; #1011343
• страница: 5 из 6

§20. Логарифм числа
При вычислении логарифма числа, обозначенного 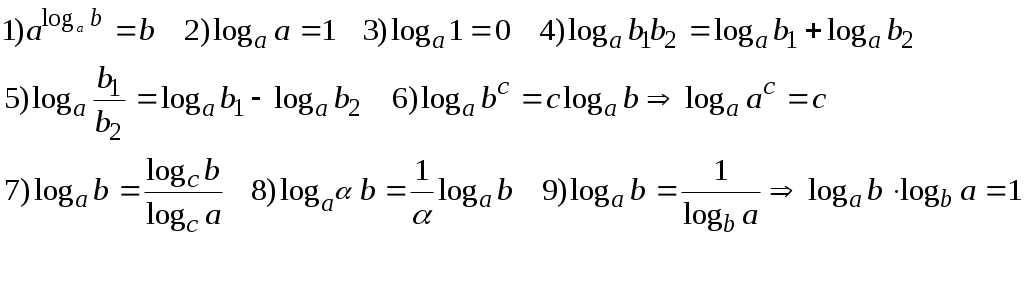, где , необходимо знать его свойства:



Пример 62. Вычислить: ;

а) Представим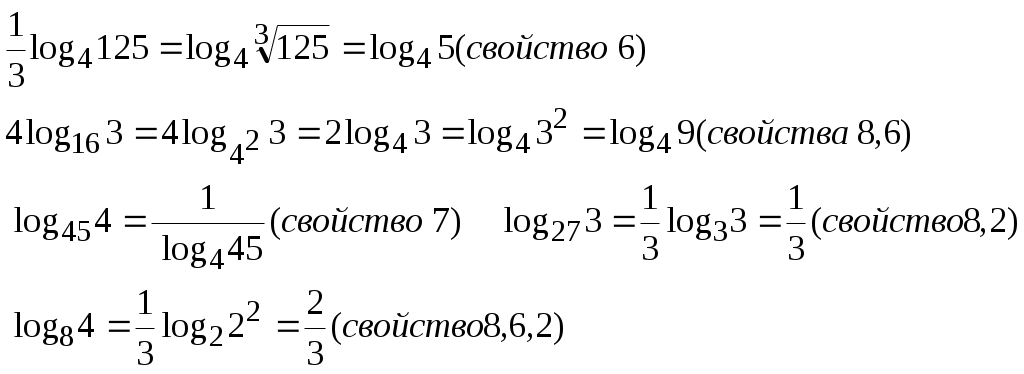

б) Продолжим вычисления, используя представленные

преобразования:


Пример 63. Вычислить: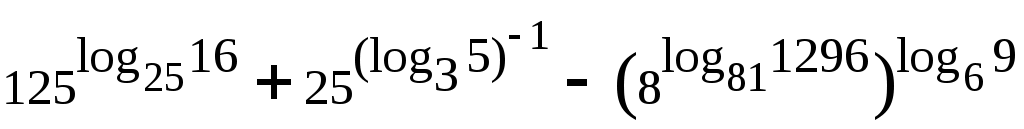

Преобразуем, используя свойства логарифма числа: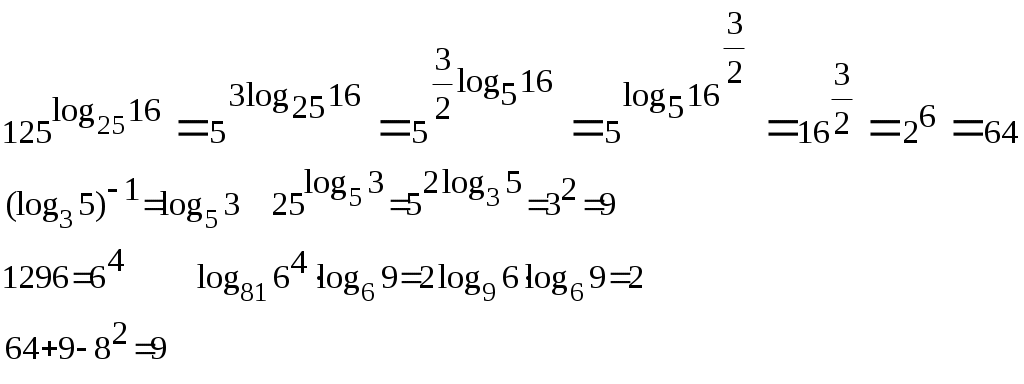




§21. Решение логарифмических уравнений
С помощью логарифмических свойств и алгебраических преобразований логарифмические уравнения сводятся к двум видам:

1) . Из равенства логарифмов с одним и тем же основанием следует равенство , которое требует решения алгебраического уравнения. Для получения правильного решения логарифмического уравнения необходимо сделать проверку полученного решения алгебраического уравнения, так как необходимо, чтобы .

2) . Замена переменной: приводит к

решению алгебраического уравнения . Получив решение

, переходят к решению уравнения

, то есть . Полученное

решение проверяется условием .

Пример 64.

а) Преобразуем левую часть уравнения

. (Использованы равенства:

).

б) Приводим полученное выражение к общему знаменателю:

или .

Проверкой подтверждается только решение .

Пример 65.

а) Заменим

б)

в)
§22. Решение логарифмических неравенств
Решение логарифмического неравенства вида

зависит от основания логарифма . При >1 переходим к решению неравенства (знак неравенства - прежний), а при

знак неравенства меняется на противоположный: . Окончательное решение логарифмического неравенства находится с учетом его области определения, то есть выполнения условий



Если основание логарифма является переменной величиной, то решение логарифмического неравенства выполняется в два этапа, когда полагается, что основание логарифма больше единицы, либо меньше единицы, но больше нуля.

Пусть 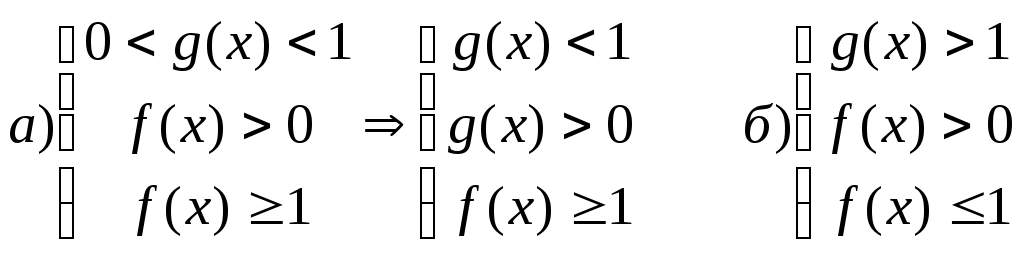Решение:



Пример 66. 0

а) Данная задача, в сравнении с той, что была описана в общем виде выше, упрощается тем, что выражение под логарифмом представлено числом 0,4<1.В этом случае 0 выполняется только тогда, когда логарифмическая функция убывает, то есть при условии

.

б) Решаем систему неравенств: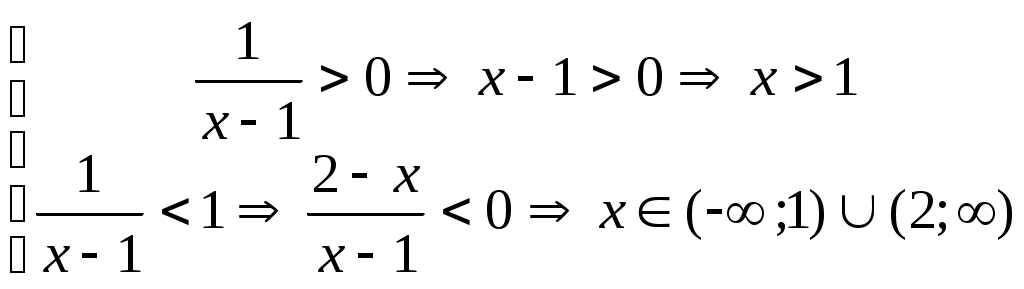


Общее решение системы: (2;).

Пример 67. 0

а) Необходимо решить систему неравенств: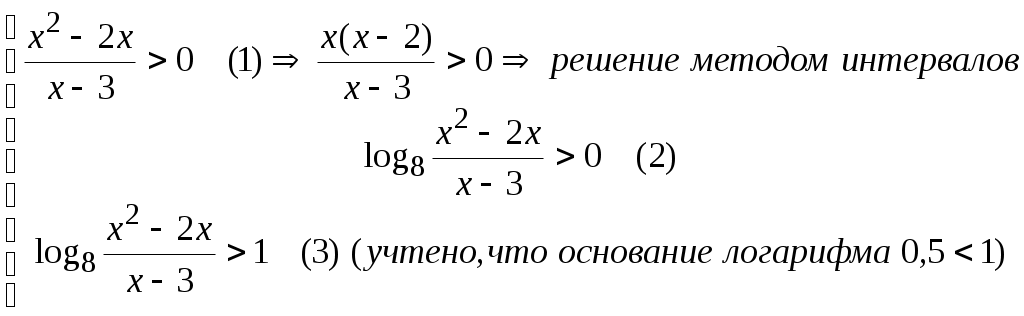



б) Решение неравенства (1):

Неравенства (2) и (3) объединяем и решаем неравенство:



Последнее неравенство решаем мотодом интервалов и получаем решение:

Пример 68. 1

а) Система неравенств будет иметь вид: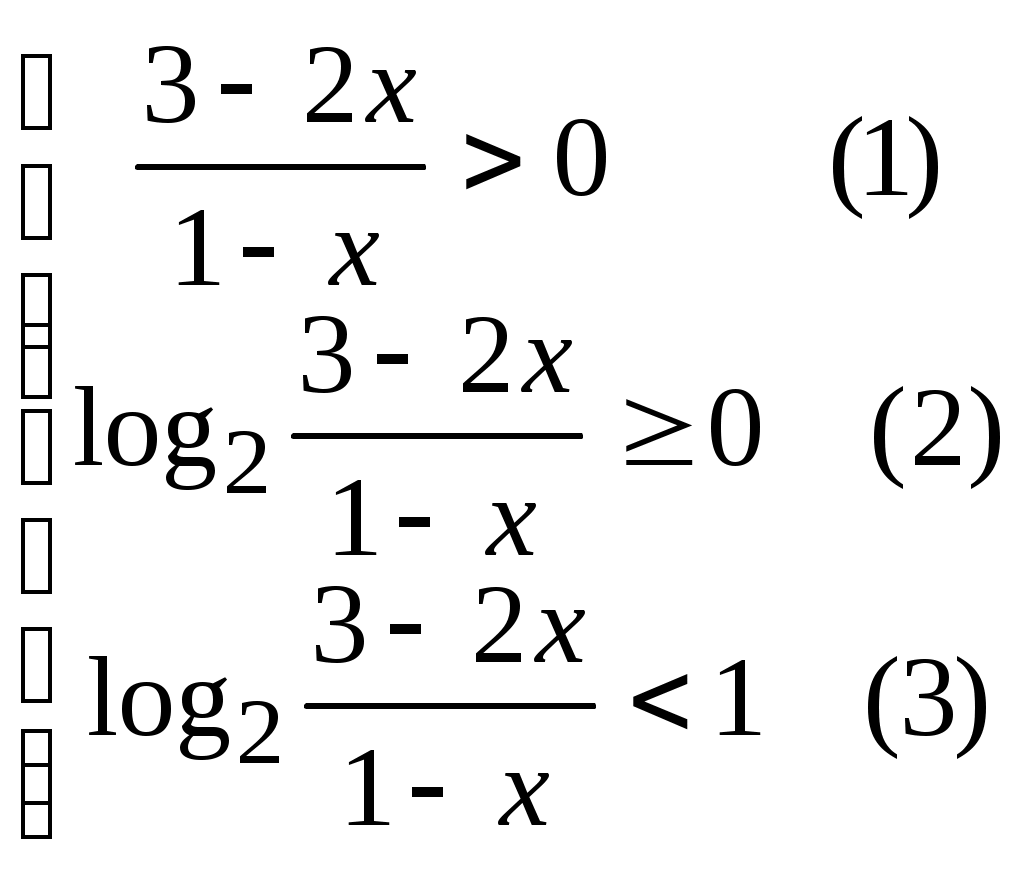



б) Решение неравенства (1):

Решение неравенства (2):

Решение неравенства (3): .

Объединим полученные решения:
§23. Область определения функции. Графики функции.
Ограничения на область определения имеют следующие функциональные выражения: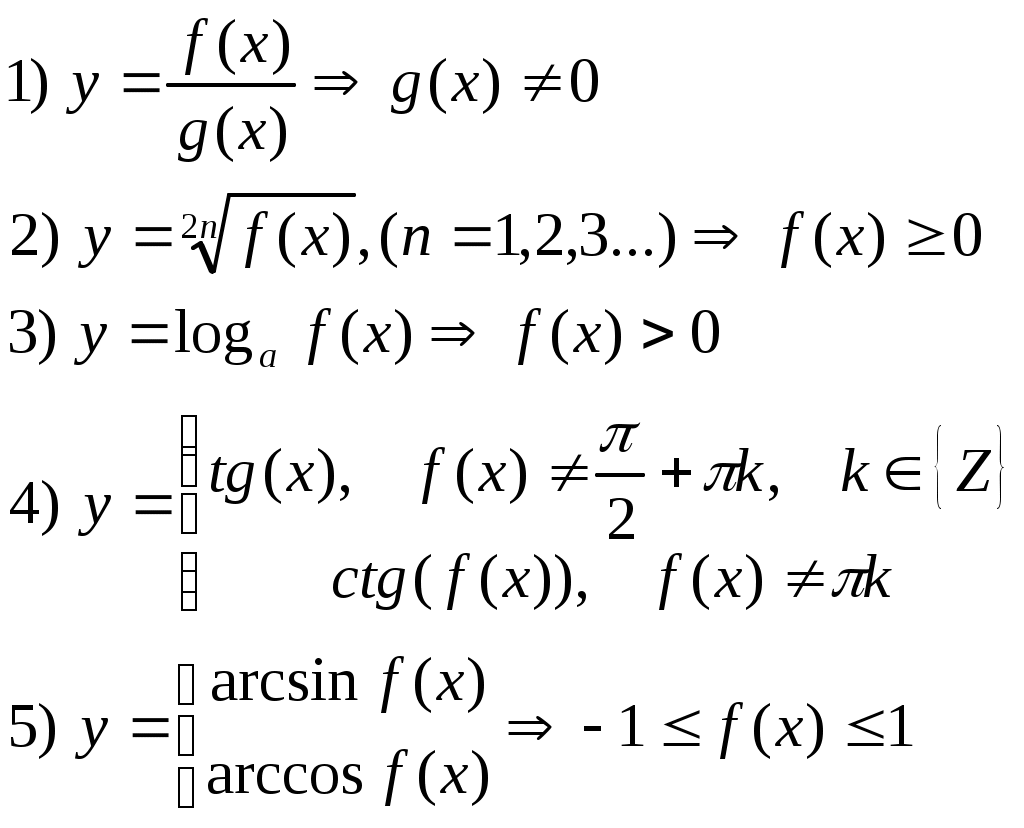



Решение данных неравенств приводит к решению задачи о нахождении области определения.

Пример 69.

Решим систему неравенств, согласно общим рекомендациям.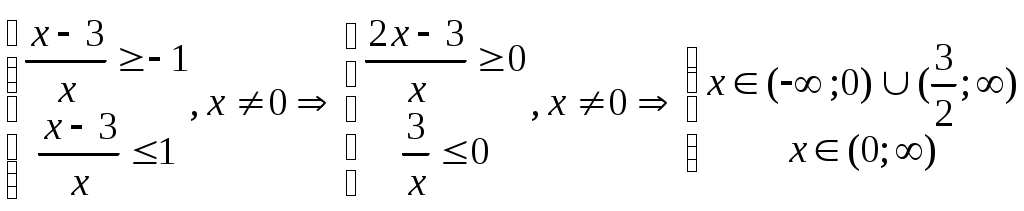

.

Решение задачи:

При построении графиков функций необходимо классифицировать функцию как линейную, дробно-линейную, степенную, показательную, логарифмическую тригонометрическую или обратно тригонометрическую. Графики простейших функций данного вида общеизвестны. Далее, необходимо учесть параллельный перенос осей координат, если функция преобразуется к виду .

При параллельном переносе новое начало осей координат находится в точке О₁ с координатами , а оси О₁Х₁ и О₁Y₁ параллельны осям

ОХ и ОY. График функции расположен относительно точки также, как располагался бы график ( ). Рекомендации к решению задач.

Задача 70: .

Начало координат О₁(0;-1) является нулевой точкой новой системы координат Х₁О₁Y₁ при параллельном переносе осей координат (О₁Х₁ и О₁Y₁ параллельны ОХ и ОY, соответственно). В новой системе координат строим гиперболу

, ветви которой расположены в первой и третьей четвертях системы Х₁О₁Y_1; учитываем, что одна из ветвей проходит через точку:



График функции отличается от графика тем, что все , поэтому необходимо все отрицательные значения заменить такими же положительными значениями .

Окончательный график представляет собой две ветви гиперболы, расположенные в первой и второй четвертях системы координат Х₁О₁Y_1.

Задача 71: .

Начало координат О₁(0;1). Строим график степенной функции в системе координат Х₁О₁Y₁ , симметричный относительно О₁, так как функция нечетна. График функции должен пройти через точку

Задача 72: .

Преобразуем выражение к виду

Тогда Строим график показательной функции в системе координат Х₁О₁Y₁ в последовательности: а) (аналог )- монотонно убывающая на всей числовой оси функция, имеющая точку пересечения с осью О₁Y₁ ( ); б) все значения

переносим в отрицательную область, сохраняя числовое значение ординаты, и получаем график функции . Построенный график должен пройти через точку

Задача 73: .

Преобразуем выражение к виду . Тогда Строим график логарифмической функции в системе координат Х₁О₁Y₁(аналог ). Область определения функции в системе координат Х₁О₁Y₁: , и график функции проходит через точку Необходимо также учесть, что графику функции принадлежит точка



Задача 74: преобразуем к виду , так как . Необходимо построить график известной функции , и все отрицательные значения ординат точек графика заменить положительными значениями.
§24. Задачи с параметрами.
Задачи с параметрами относятся к сложным задачам и имеют разную направленность. Поэтому можно дать только одну, общую для всех задач, рекомендацию: необходимо хорошо знать теоретические основы темы, обозначенной в условиях задачи.

Пример 75. При каком значении «а» функция возрастает на интервале (0;)? Указать наименьшее целое.

а) Тема задачи: исследование функции с помощью ее

производной. Возрастание функции определяется условием

.

б) . Необходимо решить неравенство ,

при условии Квадратное неравенство будет

выполняться, если при условии больший корень

уравнения равен нулю, то есть:



Рекомендации к выполнению задач:

Пример 76. При каком значении «а» функция расположена не ниже оси ОХ. Указать наименьшее целое.

Ответ: 5.

Функция графически представлена параболой, ветви которой направлены вверх, и, согласно условия задачи, ее вершина должна быть расположена в точке с координатами ( ), причем . Находим . Решаем простейшее неравенство, и, при получении ответа, учитываем условие задачи (указать наименьшее целое).