Задачи. томский политехнический университет

• Название: томский политехнический университет
• Анкор: Задачи
• Дата: 23.03.2023
• Размер: 1.98 Mb.
• Имя файла: zadachi.doc
• Тип: Сборник задач; #1011343
• страница: 1 из 6

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

«Утверждаю»

____________
“__”________2009 г.


СБОРНИК ЗАДАЧ С РЕШЕНИЯМИ

ПО МАТЕМАТИКЕ

для слушателей ЗФТШ «Перспектива» и школьников 10-11 классов
(Методические указания по школьной математике)

Томск 2009

УДК 378.146:51:6813 Сборник задач с решениями для повторения

школьного курса математики при подготовке к ЕГЭ

// Составители: Филипенко Л.А., Филипенко Н.М.; Том. политех,

ун-т. – Томск, 2009. - 42 с.

Сборник задач с решениями для повторения школьного курса математики при подготовке к ЕГЭ рассмотрен и рекомендован к изданию методическим семинаром кафедры высшей математики и математической физики (протокол №111 от 29 августа 2009г.)

Зав. кафедрой, профессор, д.ф.-м.н.____________А.Ю. Трифонов

Аннотация

Сборник содержит примеры решения задач или рекомендации к их выполнению. Рассмотрены задачи, являющиеся базовой основой для сдачи ЕГЭ по математике.

Ó Томский политехнический университет

СОДЕРЖАНИЕ

Введение……………………………………………………………..3
§1. Вычисления без калькулятора, алгебраические

преобразования ………………………………………………. 4

§2. Линейные уравнения и неравенства, содержащие

переменную под знаком модуля ……………………….......... 6

§3. Системы линейных уравнений ……………………………… 8

§4. Системы линейных уравнений, содержащие параметр………..9

§5. Задачи, связанные с квадратным выражением ……………….11

§6. Решение рациональных неравенств …………………………...13

§7. Построение графиков квадратных функций,

содержащих модуль ……………………………………………14

§8 Квадратные уравнения, содержащие параметр ………………15

§9. Решение рациональных уравнений

со степенью n 2 …………………………………………. ……16

§10. Решение нелинейных систем уравнений…..…………...........18

§11. Решение иррациональных уравнений и

неравенств……………………….…………….………………..20

§12. Прогрессии…………………………………………………….22

§13. Текстовые задачи……………………………………………...23

§14. Тригонометрические задачи………………….. ……………..26

§15. Производная функции, и ее

приложения………………………………………………. …….28

§16. Первообразная функции. Определенный

интеграл…………………………………..…..………….............30

§17. Показательные уравнения…………………………………….32

§18. Показательные неравенства……………….. ………………...33

§19. Решение системы показательных уравнений………………..34

§20. Логарифм числа………………………………………………..35

§21. Решение логарифмических

уравнений………………………………………………………36

§22. Решение логарифмических

неравенств……..……………………………………………….36

§23. Область определения функции. Графики

функций………………………………………………………...38

§24. Задачи с параметрами………………………………………...40


Введение
Сборник задач для слушателей ЗФТШ «Перспектива» и школьников старших классов содержит необходимые теоретические основы для решения задач, примеры их решения (или рекомендации к решению). Тематика задач соответствует всем разделам школьного курса математики, за исключением геометрии. Рекомендуемые задачи определяются требованиями ЕГЭ последних лет. Уровень сложности задач можно оценить как средний и выше.

§1. Вычисления без калькулятора, алгебраические преобразования.
Для выполнения расчетов без калькулятора необходимо уметь переводить периодические дроби в обыкновенные. Удобнее всего это делать по формуле для суммы бесконечно убывающей геометрической прогрессии , где - первый член прогрессии; - знаменатель прогрессии.

Рассмотрим такое задание на нескольких примерах:

Пример 1. - члены бесконечно убывающей прогрессии, где . Тогда

.
Пример 2. - члены бесконечно убывающей прогрессии, где . Тогда

.

Пример 3.

. Тогда

Пример 4. (( +2,708333…):2,5):((1,3+0,7(6)+0,(36)) ´ )´ ;

Необходимо правильно и рационально выполнить цикл вычислений. Прежде всего переведем периодические дроби в обыкновенные.

1)

.
2) .
3) .
4) .
Для выполнения некоторых задач необходимо понимать, что . Тогда,

Пример 5. , так как .

Для формирования квадрата суммы или разности под знаком корня необходимо представлять, что .

Пример 6. Вычислить .

, где . Необходимо подобрать a иb так, чтобы сумма их квадратов равнялась 5.

.

Значит . Тогда . Можно проверить, возводя в квадрат, что это действительно так

В результате, , так как .

Пример 7.

Вычислить .

, так как , то
.

IV. Для выполнения алгебраических преобразований необходимо знать свойства степенных выражений и модификации формул сокращенного умножения. Например:

1) .

2) , используем и условие

.

3) , тогда

.

Пример 8. ( + - )³.

Учтем, что ;

Тогда
.

Пример 9. ( +1)( )( )^-1.

Учтем, что , а . Тогда .

§2. Линейные уравнения и неравенства, содержащие переменную под знаком модуля.
Для решения уравнений и неравенств со знаком модуля необходимо использовать следующую схему решения.

1. Определить нулевые точки, приравняв нулю выражения, находящиеся

под знаком модуля.

2. Разделить числовую ось на интервалы полученными нулевыми

точками и решить уравнение или неравенство для каждого интервала,

убирая знак модуля в соответствии с правилом (п.III).

3. Полученное решение должно принадлежать рассматриваемому

интервалу, если решается уравнение. При решении неравенства

находится общий промежуток для полученного решения и интервала.

Пример 10. |х+12|-|х-1|=3х-8.

Нулевыми точками являются значения и . Рассматриваем последовательно интервалы: . Нулевые точки включаем в интервал, находящийся справа от нулевой точки.

В интервале , так как при любом по той же причине. Тогда получается уравнение: . Решение не принадлежит промежутку .

В интервале . Уравнение имеет решение , не принадлежащее промежутку .

В интервале . Уравнение имеет решение , и оно является решением уравнения.

Пример 11. |х-1|+ х < 5-|2х-5|.

Нулевыми точками являются значения 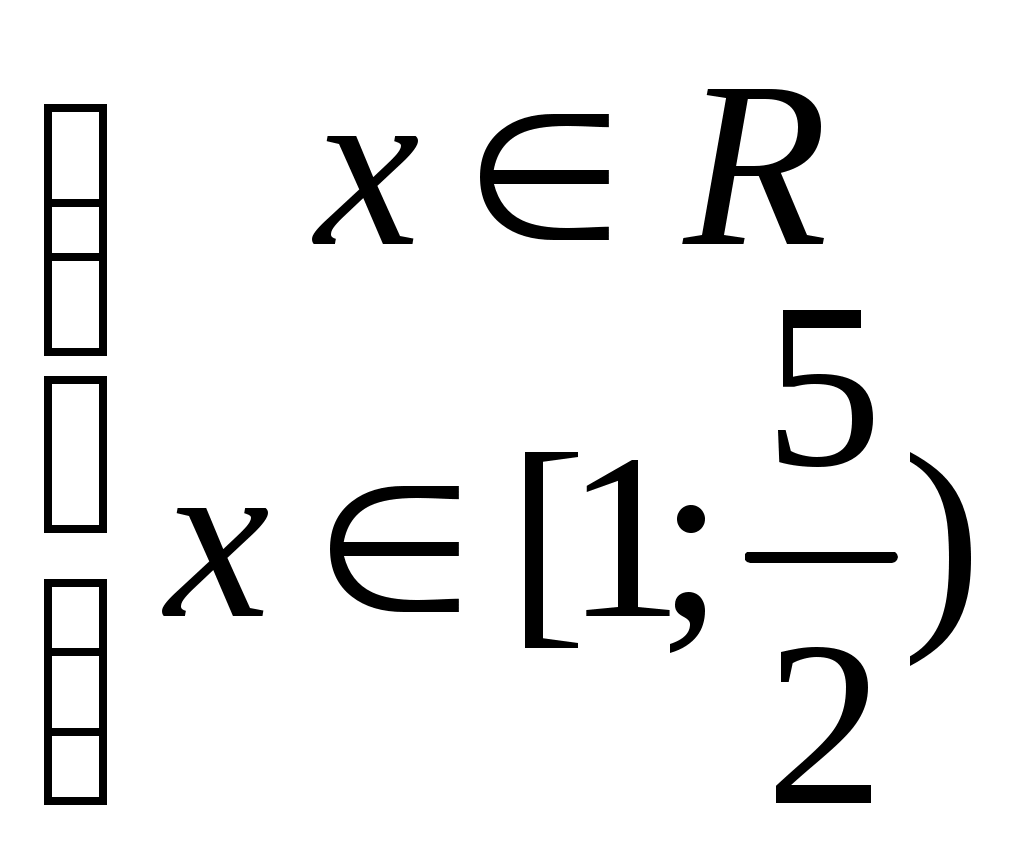и . Рассматриваем решение для интервалов: .

В интервале . Решаем неравенство . Общим решением находим .

В интервале . Решаем неравенство , что означает . Тогда решением системы является .

В интервале 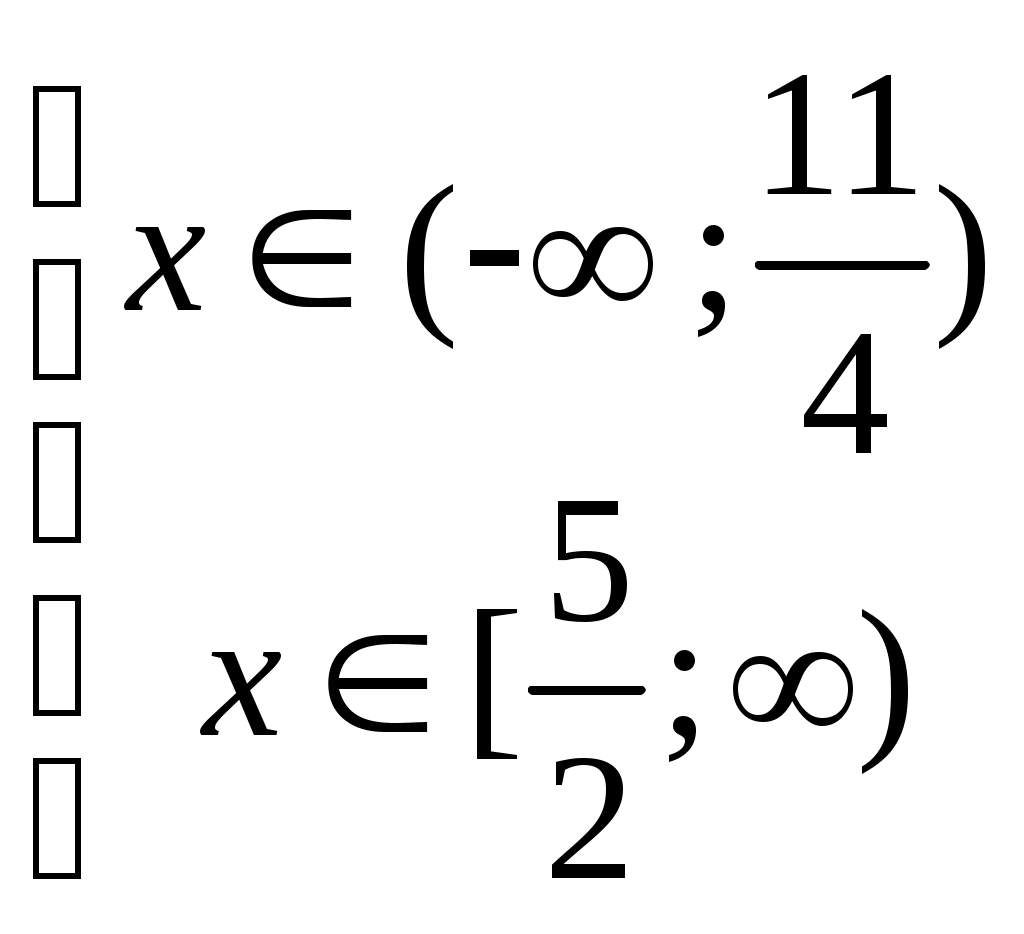. Решаем неравенство и получаем решение . Для системы решением является .

Собирая вместе полученные решения, которые имеют общие точки и , объединяем полученные промежутки в один .

§3. Системы линейных уравнений
Для решения системы трех линейных уравнений будем использовать метод исключения неизвестных.

Пример 12.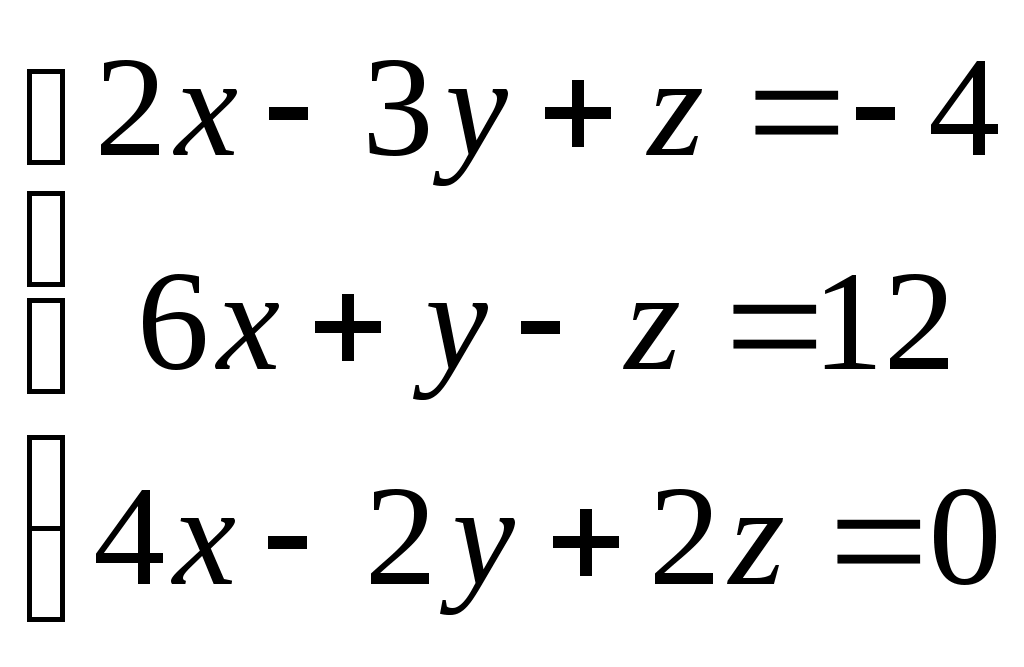

Исключим неизвестное из первого и второго уравнения: . Для этого достаточно сложить эти уравнения (левые и правые части). Уравнение или будет содержать только два неизвестных.

1. 
   Аналогично исключим из второго и третьего уравнений: . Первое уравнение умножим на 2 (обе части) для того, чтобы коэффициенты при были равны и
   

противоположны по знаку .

Складывая эти уравнения, получим или .

2. 
   Тогда из уравнения . Зная и из л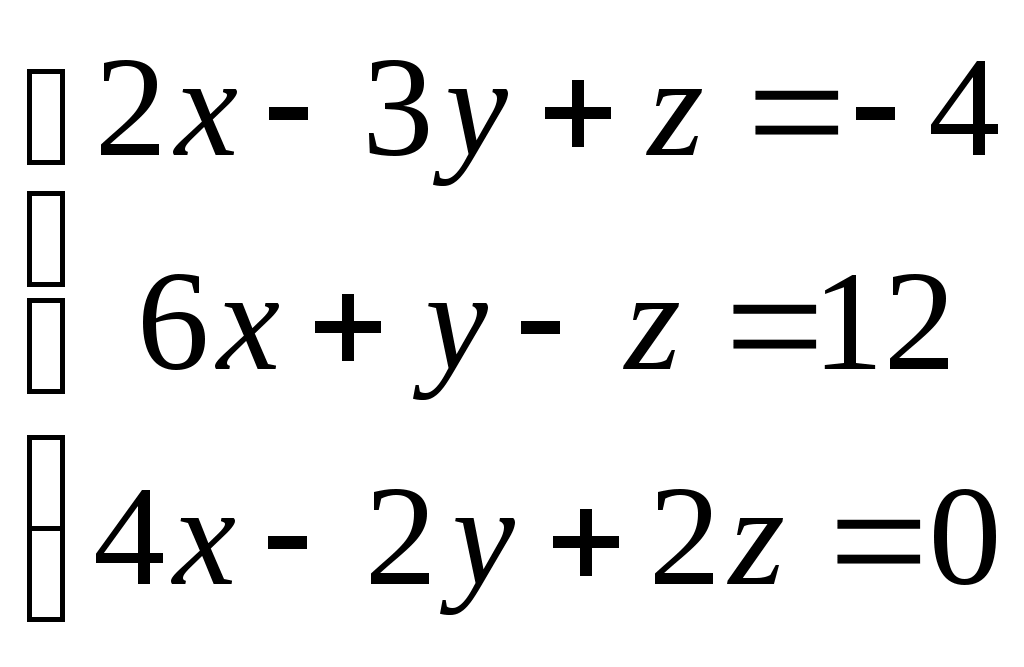юбого уравнения системы можно найти значение .
   

Пример 13.

Исключаем из уравнений один и два:

. Для этого умножим уравнение один на (-2):

. Суммируем уравнения и получаем .

Исключаем из второго и третьего уравнений:

. Суммируем их и получаем .

Решаем систему из уравнений , умножая первое

уравнение на 2 и суммируя: получим

. Подставляем и находим . Из

любого уравнения системы находим , подставляя

(первое уравнение: ).

§4. Системы линейных уравнений, содержащие параметр.
Для решения подобных задач необходимо знать, что линейная система вида 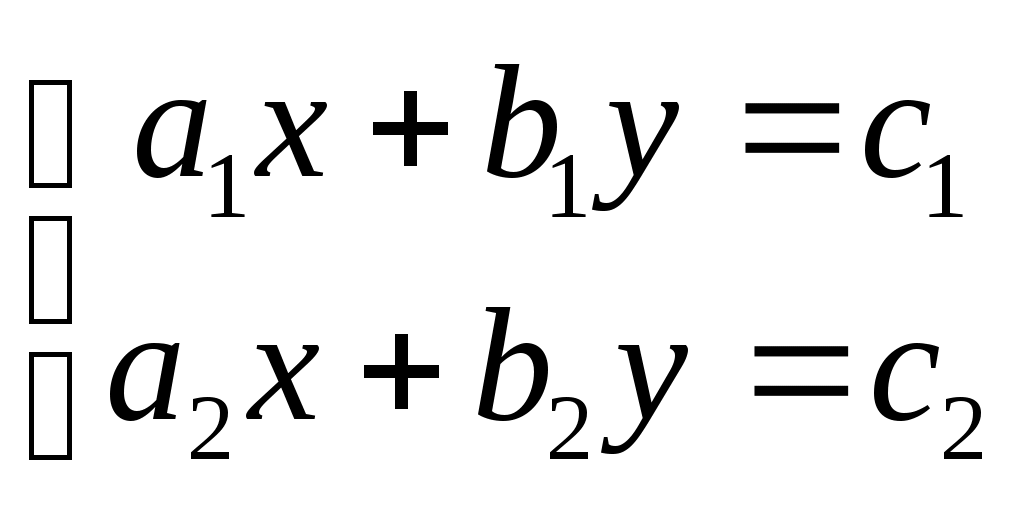(1) имеет единственное решение, при ; имеет множество решений, если и не имеет решений, если .

Во избежание ошибок при использовании метода подстановок, которым чаще всего и решается система (1), можно освоить несложный метод Крамера, использующий понятие определителя системы, обозначение и вычисление которого следующее: 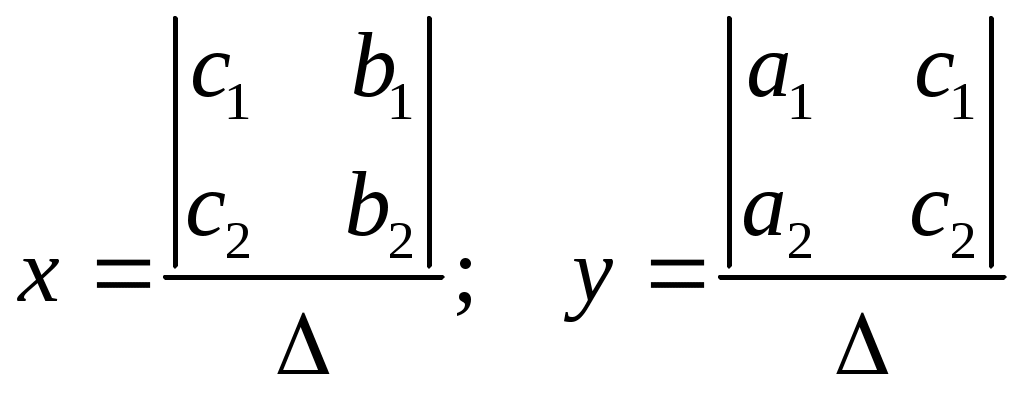- определитель системы. Тогда неизвестные и находятся в виде , то есть в последовательно заменяется первый столбец (коэффициенты при ) или второй столбец (коэффициенты при ) на столбец свободных членов системы (правая часть системы). Вычисления определителей выполняют по тому же правилу, что и для : .
Решим методом Крамера систему без параметров: .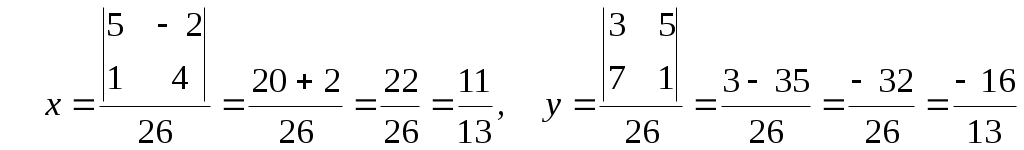


.
Проверка: 1) (верно)

2) (верно).
Пример 14.

Единственное решение система имеет при условии или . В результате или , то есть .

В помощь к выполнению подобных задач в контрольной работе решим следующую задачу.

Пример 15. . Найти значение параметра удовлетворяющее

условию .

Решение: Чтобы правильно найти 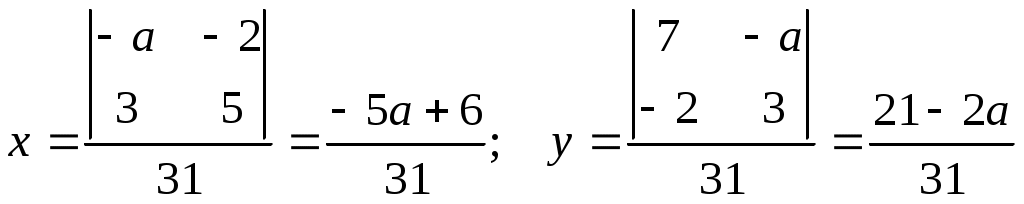, необходимо всегда систему записывать в стандартном виде (1), то есть: . ; .

Условие ведет к решению неравенства
.

Ответ: .
§5. Задачи, связанные с квадратным выражением.
Квадратное выражение используется в различного вида задачах: квадратных уравнениях, неравенствах, геометрическом представлении функции в виде параболы. Для правильного решения задач необходимо знать:

1) Уравнение всегда можно привести к виду . Тогда при ( - дискриминант уравнения) корни уравнения определяются условием: . Данные условия используют для нахождения корней по теореме Виета.

Пример 16. Найти корни квадратного уравнения по теореме Виета: х²-10х+9=0.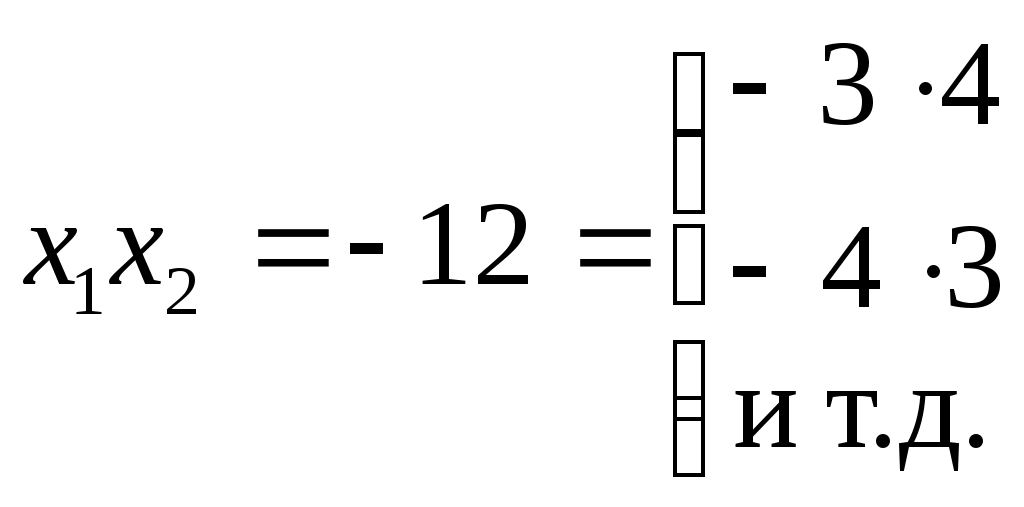

. Выбираем сомножители, удовлетворяющие условию , то есть .

2) Разложение на сомножители: возможно только при .

3) Выделение полного квадрата означает приведение к виду и выполняется по схеме: , где . Практически, необходимо из выражения вынести множитель , поделив на него все слагаемые, затем разделить коэффициент перед пополам и выделить квадрат суммы или разности в зависимости от знака перед , затем вычесть квадрат числа, закрытого в скобке и выполнить действия между числами, после этого умножить на вынесенный множитель полученные скобки и числовое значение вне скобок.

Пример 17. ; Пояснение: . Если перед множитель 1 , то выделение полного квадрата упрощается: ; .

4) Выделение полного квадрата помогает очень просто решить геометрическую задачу по построению параболы, которая является геометрическим образом квадратной функции . Вершина параболы находится в точке , если уравнение параболы привести к каноническому виду: . Выделение полного квадрата практически решает данную задачу: . Пример 18. . Кроме этого, можно использовать и известные формулы для значений: . Для полного построения параболы необходимо также найти точки пересечения с осями координат: с - корни уравнения ; с . Направление ветвей определяется знаком множителя перед . Ветви расположены вверх при и вниз при .

5) Решение квадратного неравенства проще выполнять с помощью схематического построения параболы, учитывая только направление ветвей и существование корней уравнения , то есть значений .

Пример 19. Решить квадратное неравенство: ;

. Решаем уравнение

. Можно было заметить, что

. Неравенство имеет решение ,

так как парабола расположена ветвями вверх и только касается оси

в одной точке .

6) Решение квадратных уравнений и неравенств, содержащих модуль

необходимо выполнять, убирая модуль по известным правилам,

изложенным в §2.

Пример 20. .

. Нулевые точки . В интервалах

выражение имеет соответственно знаки

. Тогда для интервалов решаем уравнение

и принадлежат данным

интервалам и являются решениями. В интервале

и решаем уравнение или

. Решениями являются значения ,

принадлежащие указанному интервалу. Полный ответ: .
Пример 21. .

Выражение имеет нулевые точки и в интервалах имеет соответственно знаки . Для интервалов , а неравенство имеет вид и имеет решение . С учетом рассматриваемых интервалов решением являются промежутки . В интервале и решаем неравенство . Решениями будут промежутки . Общим решением системы является решение . Объединяем полученные решения и , и окончательный ответ: .
§6. Решение рациональных неравенств.
Решение рациональных неравенств выполняется по схеме: все слагаемые переносятся в левую часть (сравнение возможно только с нулевой правой частью). Затем левая часть приводится к общему знаменателю.

Находятся нулевые точки числителя и знаменателя, а числовая ось делится ими на интервалы. Если все линейные множители записаны в виде , то самый правый интервал имеет знак , а затем знаки в интервалах чередуются. Решение неравенства совпадает с интервалами того же знака, что и знак неравенства. Необходимо учесть, что множители в четных степенях не влияют на знак неравенства и могут быть полностью исключены из рассмотрения, если знак неравенства строгий; значение, соответствующее нулю, также является решением, если знак неравенства нестрогий.

Пример 22.

. Неравенство строгое, поэтому исключаем точку , а затем исключаем из рассмотрения . Интервалы имеют знаки . Значит решением являются промежутки . Точка не принадлежит указанным промежуткам.

Пример 23. . Решением является и .

Пример 24. ³ .


.
Умножим на . Выражение при любых , так как , а коэффициент при положителен (парабола находится выше оси ). Значит, решаем неравенство . Выражение необходимо представить в виде , то есть разложить на сомножители, если это возможно.

Нулевые точки . Интервалы имеют знаки . Решением неравенства являются промежутки .
§7. Построение графиков квадратных функций,

содержащих модуль.

Пример 24.

Рассмотрим построение функции . При решении уравнения определено, что в интервалах , в интервале . Поэтому необходимо построить функции и , и взять части графиков для соответствующих интервалов. Для построения параболы найдем координаты вершины и точки пересечения с осями координат:



, то есть . Точки пересечения с , с .

Для построения параболы выполним аналогичные действия:

.

Координаты вершины параболы . Ветви параболы направлены вниз. Точки пересечения с осями координат те же, что и для .

На рисунке показан график функции .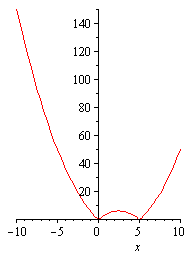




§8. Квадратные уравнения, содержащие параметр.
При решении подобных уравнений обычно используются определенные знания о дискриминанте уравнения и его связи с корнями данного уравнения.

Пример 25.

При каких значениях уравнение имеет одно решение?

Одно решение квадратное уравнение имеет при . Найдем . Решим уравнение . и . Поэтому .

Пример 26.

При каких значениях уравнение не имеет действительных корней?

Квадратное уравнение не имеет решения в области вещественных значений при . Найдем . Решим неравенство . Интервалы имеют знаки . Поэтому решением является промежуток .

Необходимо также знать, что при квадратное уравнение имеет два решения .

§9. Решение рациональных уравнений

со степенью n 2
При решении рациональных уравнений со степенью n 2 необходимо понимать, что в зависимости от вида уравнения можно:

1. 
   преобразовать его левую часть (правая часть равна нулю) в произведение сомножителей со степенью не выше двух, и затем приравнять каждый из них нулю, решив полученные уравнения известным способом.
   

Пример 27.



Выполняем преобразование: Действие сокращения на невозможно, так как множитель содержит неизвестное , и теряется корень уравнения. Далее, приравниваем нулю:

а)

2. 
   при n=4 узнать вид биквадратного уравнения, и решить его известным способом.
   

Пример 28.

.

Делаем замену переменной и решаем квадратное уравнение

1.

3. 
   некоторые виды уравнений можно свести к квадратному заменой переменной.
   

Пример 29. .

Преобразование:

Заметим общую часть . Тогда уравнение примет вид



Приводим к общему знаменателю и решаем квадратное уравнение

Приравниваем: и .

Решаем уравнения и получаем корни .

4) подобрать корень , если он целый, учитывая, что целыми корнями рационального уравнения с целыми коэффициентами могут быть только делители свободного члена. Затем преобразовать уравнение к виду , где выражение получено делением многочлена, стоящего в левой части уравнения(правая часть равна нулю), на многочлен . Деление выполняется столбиком. Корни получают, приравнивая нулю сомножителей левой части уравнения.

Пример 30.

.

Данное уравнение не решается ни одним из способов, описанных в пп.1,2,3, поэтому попробуем подобрать корень из делителей числа 6: Подходит Поделим левую часть уравнения

на :

_ 