Задачи. томский политехнический университет
 Скачать 1.98 Mb.
|
|
§13. Текстовые задачи Текстовые задачи – это задачи на составление уравнений на основании зависимости, данной в условии задачи. Основные этапы решения задачи. 1) Выбор одной из неизвестных величин, входящих в условие задачи, и обозначение ее какой-либо буквой (например  ). Иногда удобно ввести две или более неизвестных. В большинстве случаев для этого берут искомую величину, то есть ту, которую требуется определить по условию задачи. Но иногда бывает целесообразно обозначить через какую-нибудь другую неизвестную величину, связанную с искомой. Удачный выбор неизвестной величины облегчает составление и решение уравнения. 2) Выражают через (или другие введенные неизвестные) все неизвестные величины, входящие в условие задачи. 3) Составление уравнений (одного или более) на основании зависимости между величинами, данной в условии задачи, и их решение. 4) Проверка (по условию задачи) обязательна, так как корень уравнения может не быть решением задачи. Различают задачи, где используется процентное соотношение между величинами, или даны соотношения между ними в частях; задачи на движение и задачи на выполнение той или иной работы. Пример 40. Имеется 5л 70%-го раствора серной кислоты. Сколько литров 80%-го раствора серной кислоты нужно долить в этот раствор, чтобы получился 72%-й раствор серной кислоты? (задача на процентное соотношение) Пояснение. В 5 л 70% раствора серной кислоты содержится  л серной кислоты. Если за взять искомый объем 80% раствора, то в нем будет содержаться серной кислоты. Тогда ( )серной кислоты должны составлять 72% полученного ( ) литров объема, то есть  - это искомое уравнение задачи. Решаем его:  л.Пример 41. Первый сплав содержит металлы в отношении 1:2, а второй – те же металлы в отношении 2:3. Из скольких частей обоих сплавов можно получить третий сплав, содержащий металлы в отношении 17:27? (задача на отношения в частях) Пояснение. Весь объем первого сплава разделен на 3 части (соотношение 1:2) и содержит 1/3 одного металла и 2/3 другого металла. Аналогично, весь объем второго сплава разделен на 5 частей (соотношение 2:3) и содержит 2/5одного металла и 3/5 другого металла. Третий, полученный сплав, имеет соотношение металлов 17:27(44части), то есть должен содержать 17/44 одного металла и 27/44 другого металла. Пусть взято (в долях) 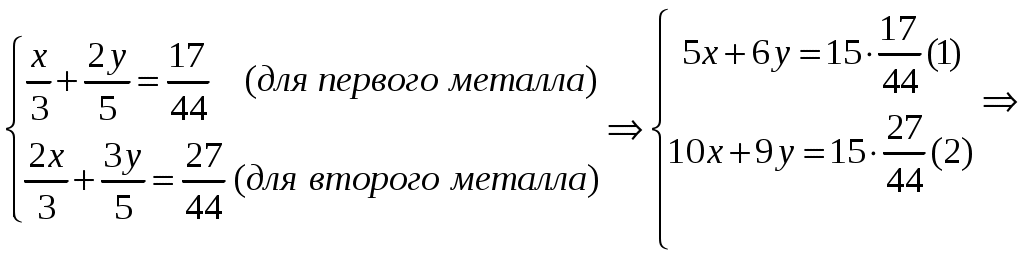первого сплава и  второго сплава. Тогда существуют равенства Поделим (1) на (2):  , то есть нужно взять 9 и 35 долей (частей) первого и второго сплава, соответственно.Пример 42. Поезд был задержан на 15 минут, поэтому, чтобы прибыть на станцию по расписанию, проходил оставшийся до нее путь в 120 км, увеличив скорость по сравнению со скоростью по расписанию в 1,2 раза. С какой скоростью прошел поезд 120 км? (задача 11 блока 4 на движение) Пояснение. Возьмем за 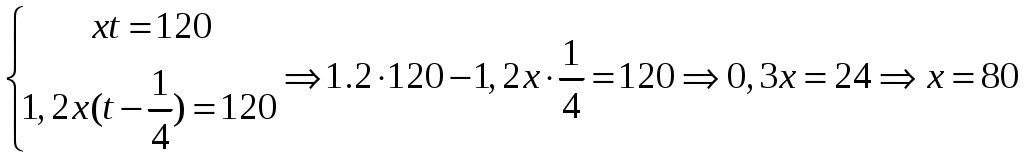скорость движения поезда до задержки и  - время движения. Тогда, согласно закону физики,  . По условию, скорость увеличена в 1,2 раза, а время уменьшено на 15 мин.(задержка поезда), то есть ¼ часа. Расстояние осталось прежним. Отсюда . Система уравнений имеет вид: км/час.Скорость  км/час.Пример 43. В бассейн проведены три трубы. Через первые две вода заливается, через третью вытекает. Через одну первую трубу бассейн может наполниться за 2 часа, через одну вторую за 5 часов, а через третью трубу вся вода из наполненного бассейна может вытечь за 10 часов. За какое время наполнится бассейн, если открыть все три трубы? (задача 12 блока 4 на выполнение работы) Пояснение. Пусть  - объем бассейна. Тогда, скорость вытекания воды из первой трубы  , из второй - , из третьей- . Время, когда открыты все трубы, обозначим . Составляем . Знак (+) означает, что труба работает на заполнение, а знак (-) – на вытекание. После преобразования ( деления на величину )получим   (часа)=1ч45мин.§14. Тригонометрические задачи Тригонометрические задачи делятся на несколько типов: Вычисление тригонометрических выражений; доказательство тригонометрических тождеств; решение тригонометрических уравнений и неравенств. Но в каждом обозначенном типе задач используются одни и те же тригонометрические формулы, количество которых достаточно велико. Приведем те формулы и тригонометрические преобразования, без знания которых большинство тригонометрических задач решить невозможно.  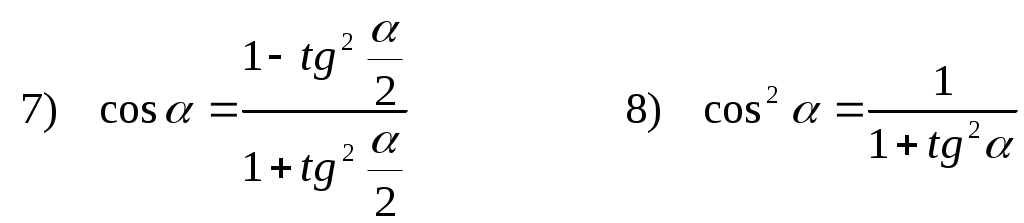    Приемы, используемые в решении задач:       Пример 44. Вычислить  .Воспользуемся преобразованиями: а)   (использован прием(3) из списка и формула  )б)  При делении (а) на (б) получим  .Пример 45. Вычислить  Преобразуем   При этом  Выражение  Пример 46. Решить уравнение  Необходимо учесть, что решение уравнения не должно содержать тех значений, которые подпадают под условия:  Преобразуем  приведем уравнение к общему знаменателю)    - решение уравнения.§15. Производная функции, и ее приложения Наиболее сложными задачами в данной теме являются задачи, в которых необходимо использовать геометрический или механический смысл производной, а также задачи на исследование функции. Необходимо знать, что: 1)  - производная функции  , вычисленная в точке , равна тангенсу угла наклона касательной, проведенной к графику функции в точке с координатами  , где  .2) уравнение касательной к графику функции в точке с координатами (  ) может быть записано в виде  Также полезно знать, что уравнение прямой через две известные точки с координатами (  может быть записано в виде  . Алгебраическими преобразованиями можно данное уравнение привести к виду  , где  - угловой коэффициент прямой. 3)  - скорость движения материальной точки, вычисленная в момент времени .4) Решение неравенства  0 и  0 определяет интервалы монотонного возрастания и убывания функции, соответственно. Эти интервалы должны принадлежать области определения функции. 5) Условие =0 определяет точку , в которой функция достигает своего максимума или минимума, если эта точка принадлежит области определения функции и производная функции в окрестности точки меняет знак, то есть  0, а  0 или наоборот, где - малое положительное значение Пример 47. В каких точках касательные к графику функции  имеют угол наклона к оси ОХ, равный 45? Напишите уравнения этих касательных. а) Найдем производную функции:  б) По условию задачи угол наклона касательных к графику функции должен быть равен  ,то есть  в) Решим уравнение   и вычислим значение  г) Запишем уравнение касательных: при  при  Пример 48. На параболе y=x2 взяты две точки с абсциссами  Через эти точки проведена секущая. В какой точке параболы касательная к ней параллельна проведенной секущей? а) Определим уравнение секущей, используя уравнение прямой, проходящей через две известные точки. Для этого вычислим  Уравнение секущей:  ; Угловой коэффициент этой прямой равен 4 (множитель перед  , если ).б) Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому производная функции y=x2 должна быть равна 4, то есть  Окончательно, получаем ответ:(2;4) Для решения задачи необходимо использовать условие перпендикулярности двух прямых  и  в виде  Пример 49. Найти угловой коэффициент прямой, соединяющей точки экстремума функции y=x3-6x2+9x+1. а) Найдем точки экстремума функции. Для этого приравняем нулю производную функции y=x3-6x2+9x+1 и решим уравнение  . В окрестности точек  производная меняет знак, точки принадлежат области определения функции (-;) и являются точками экстремума. б) Вычислим  Запишем уравнение прямой, проходящей через две известные точки с координатами (1;5) и (3;1)  . Угловой коэффициент прямой равен (-2). Пример 50. Найти минимальное целое значение параметра к, при котором функция y=x3+5x2+kx+6 не имеет экстремума. а) Найдем производную функции y=x3+5x2+kx+6. Так как по условию задачи функция не должна иметь экстремума, то 0, то есть  .б) Уравнение  не имеет решения, если дискриминант  0, то есть   . Минимальное целое значение данного неравенства  . |