|
|
Задачи. томский политехнический университет
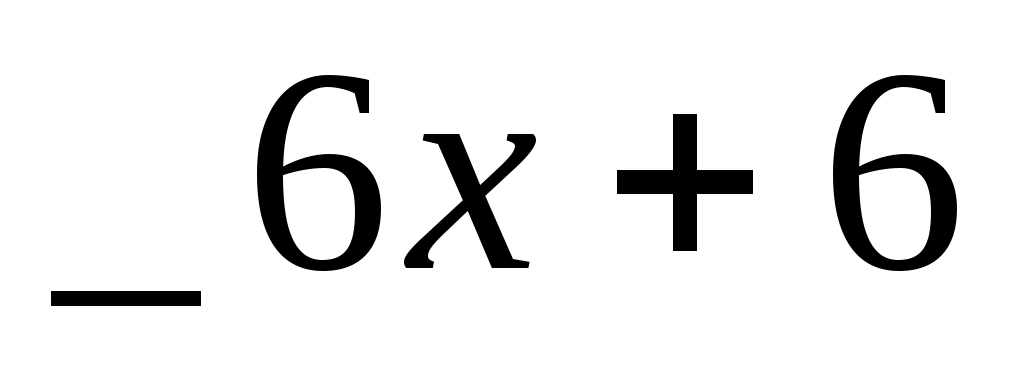
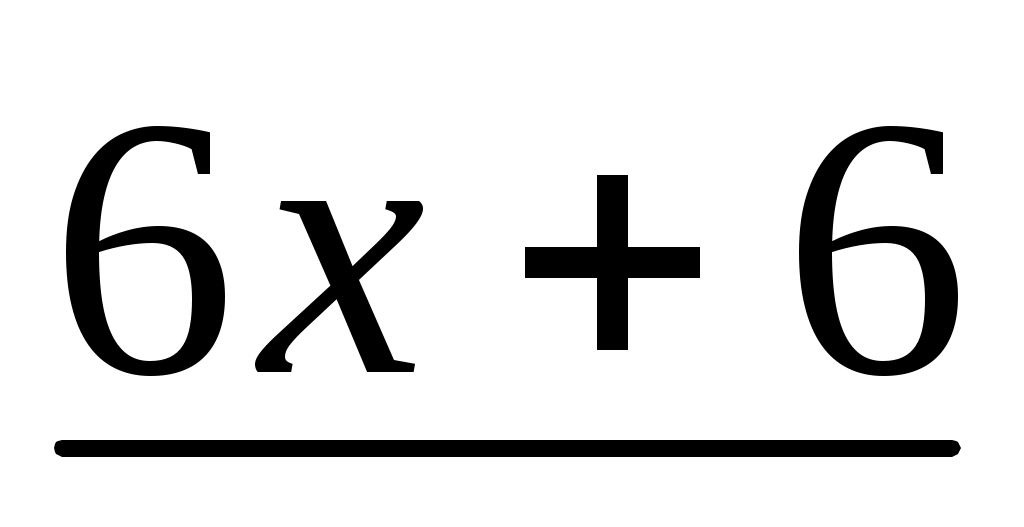
0
В результате, записываем уравнение в виде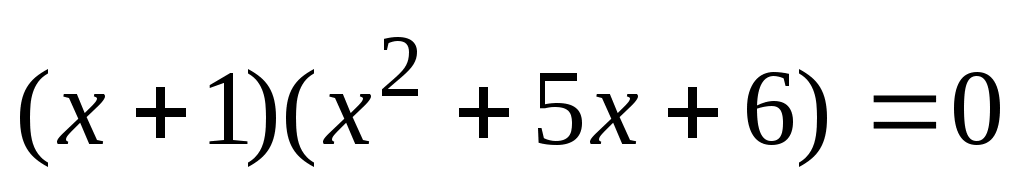 и получаем корни и получаем корни 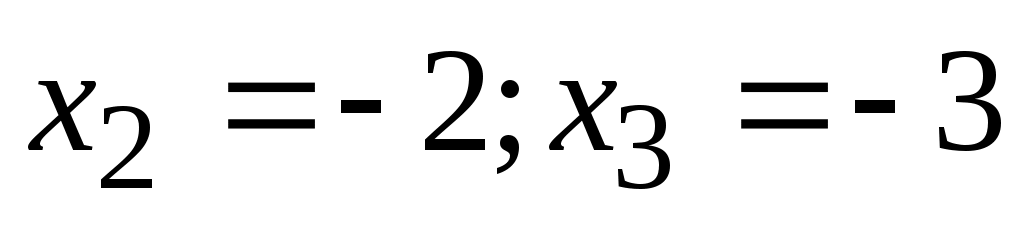 , решая квадратное равнение , решая квадратное равнение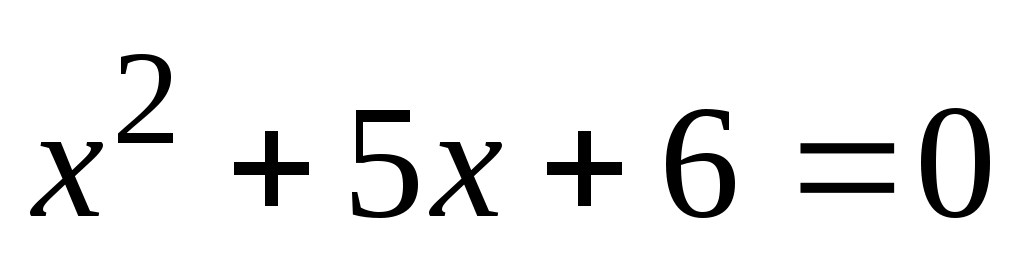 . .
5) знать специальный вид уравнения со степенью n=4:
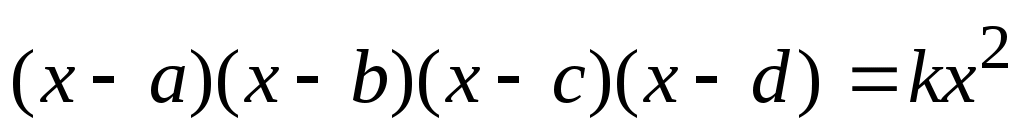 , для которого выполняется одно из условий , для которого выполняется одно из условий 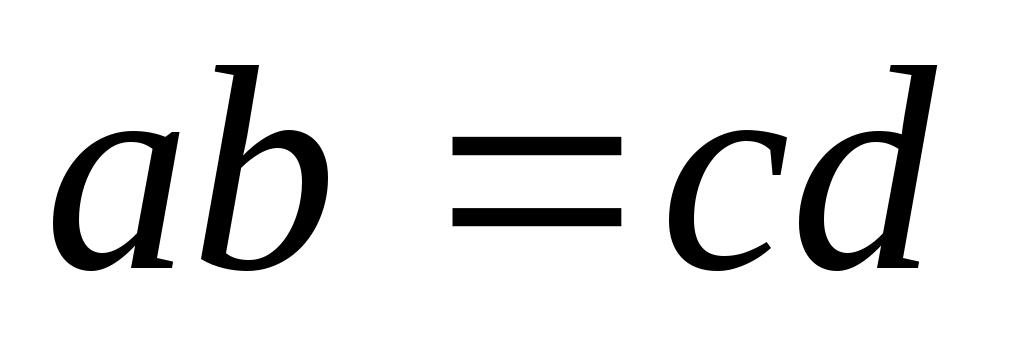 или или 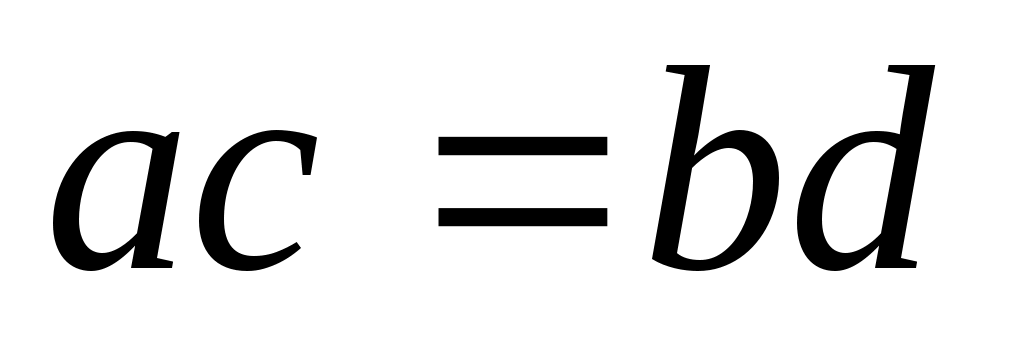 или или 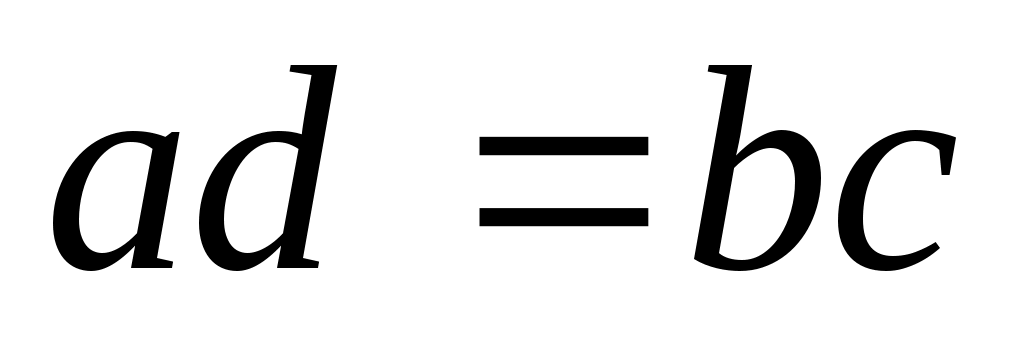 . .
Тогда (пусть 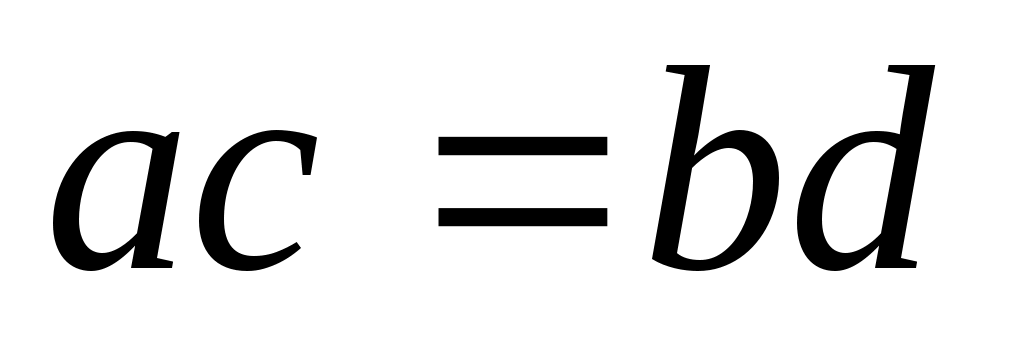 ) в уравнении выполняются преобразования: ) в уравнении выполняются преобразования:
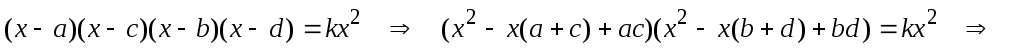 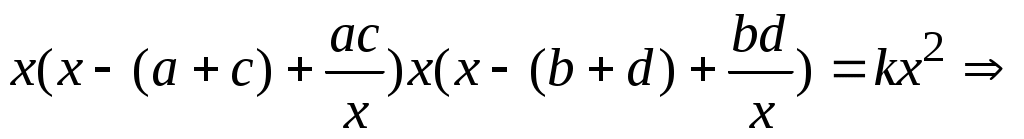  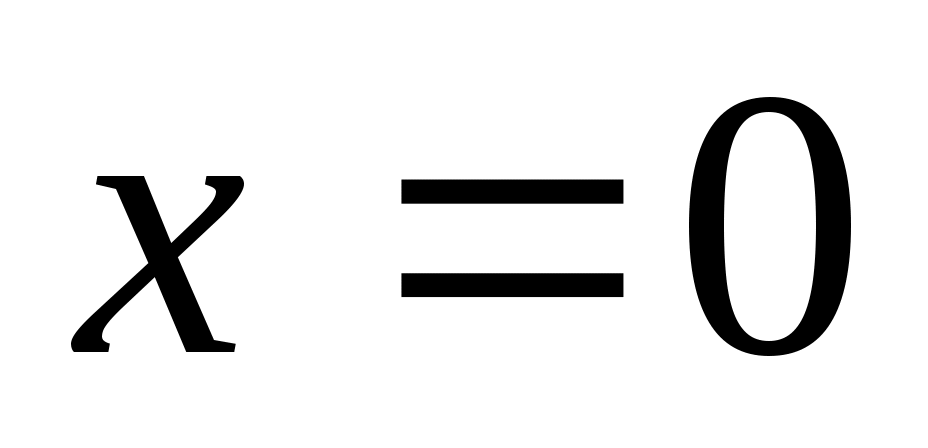 не является корнем уравнения, поэтому сократим обе части уравнения на не является корнем уравнения, поэтому сократим обе части уравнения на 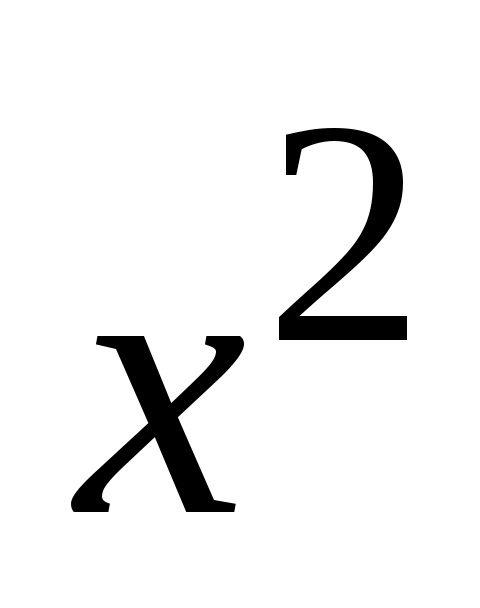 и, так как и, так как
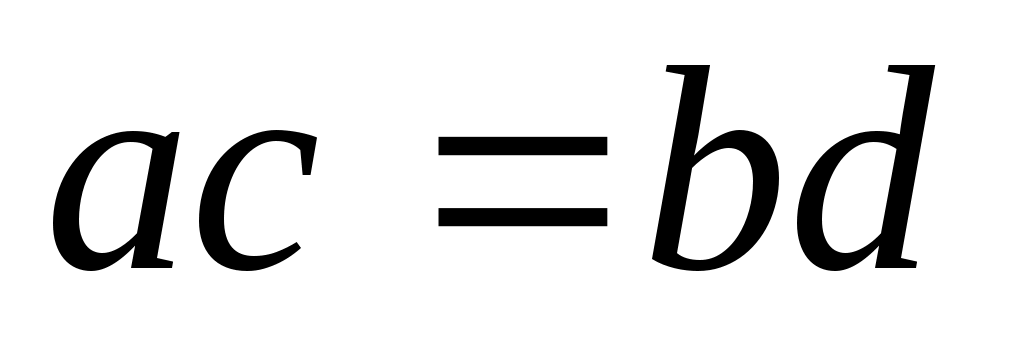 , заменим , заменим 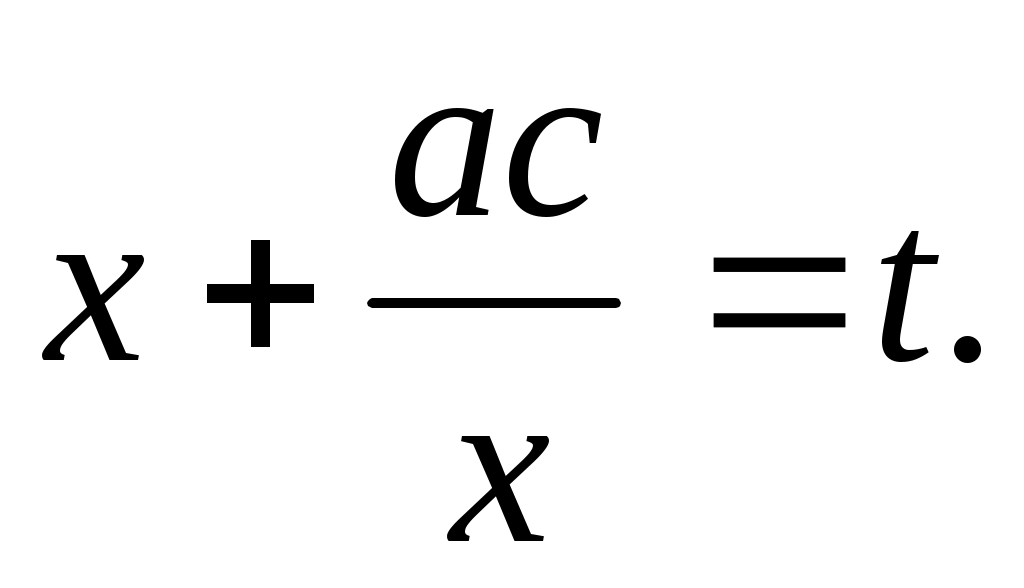 Получим Получим 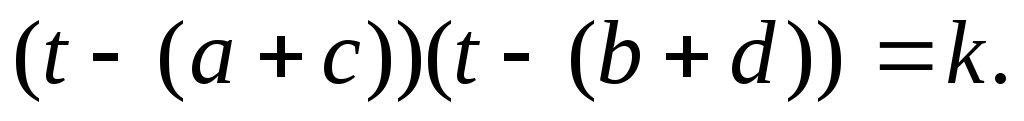 Это уравнение квадратное, решаем его и находим корни. Затем приравниваем Это уравнение квадратное, решаем его и находим корни. Затем приравниваем 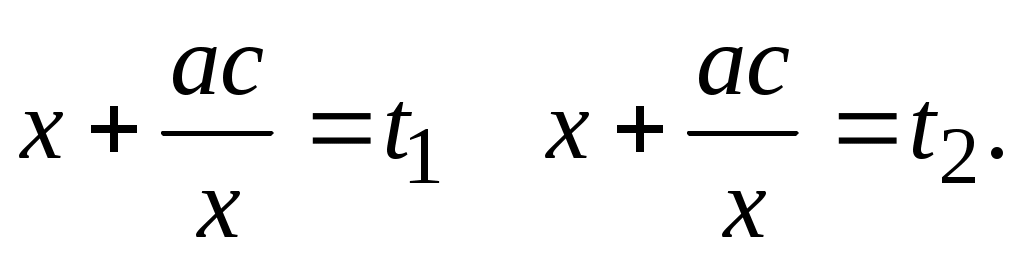 Окончательно, находим корни исходного уравнения. Окончательно, находим корни исходного уравнения.
Пример 31.
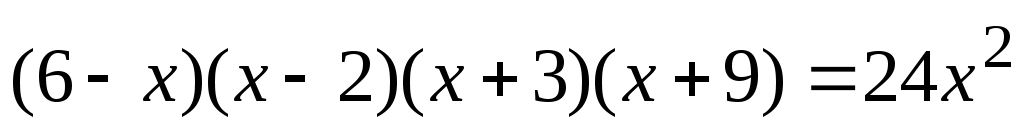 . .
Выполним преобразования так, чтобы уравнение имело стандартный вид, указанный в п.5:
 . Определим, что 6(-3)=2(-9) и запишем уравнение в виде . Определим, что 6(-3)=2(-9) и запишем уравнение в виде 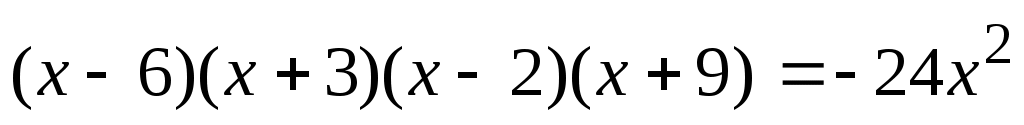 . Далее решаем уравнение по описанной схеме. . Далее решаем уравнение по описанной схеме.
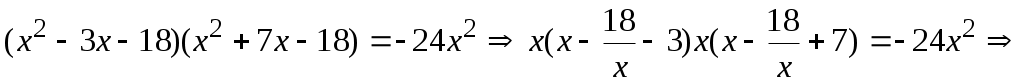

а) 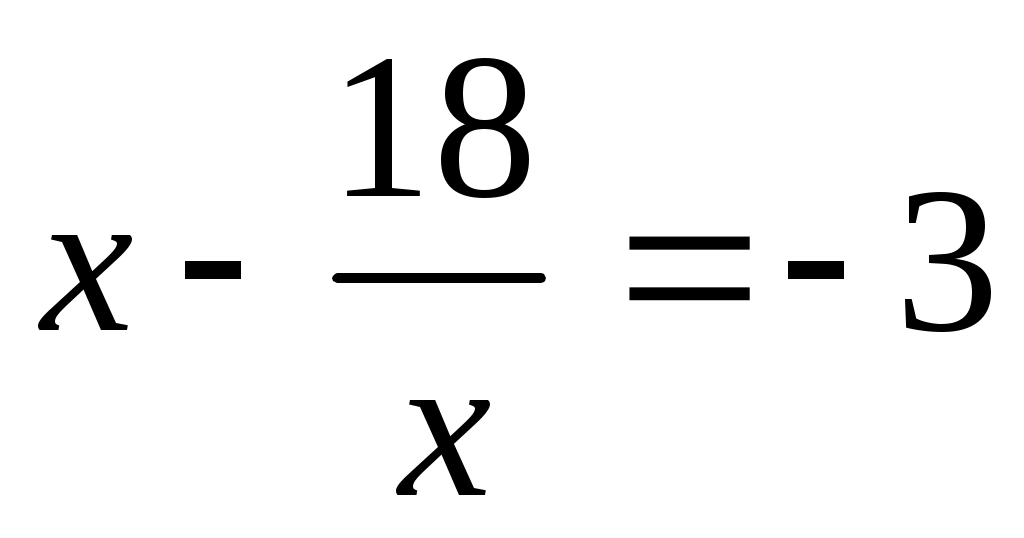 б) б) 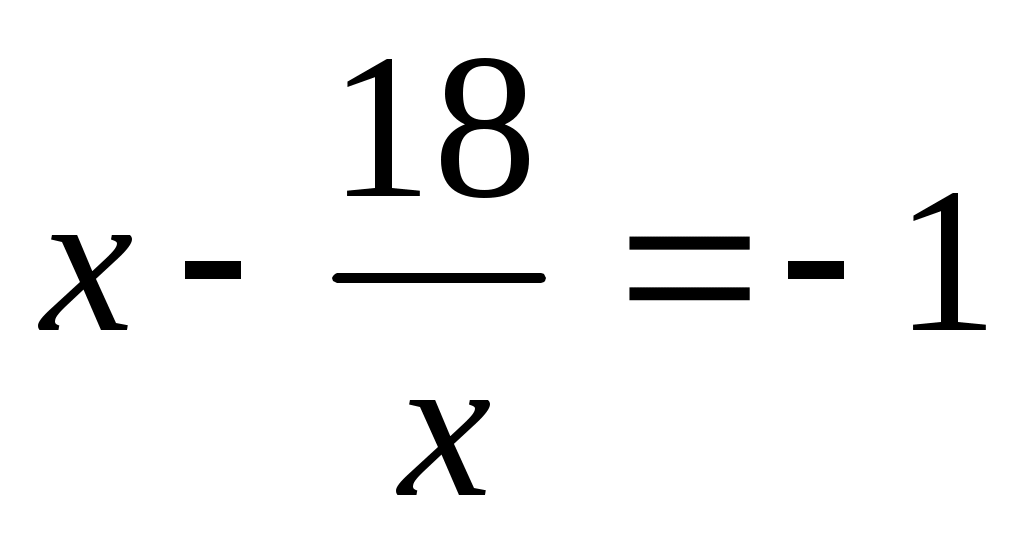
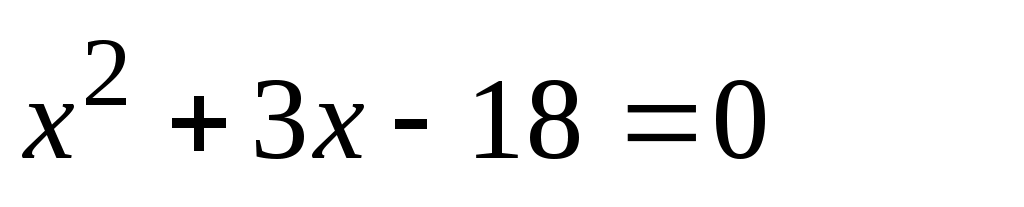 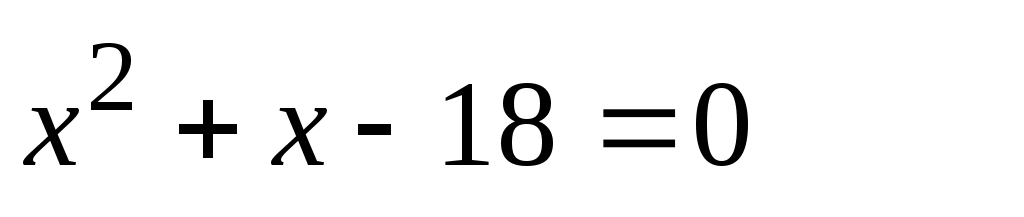

§10. Решение нелинейных систем уравнений
Рекомендуется знать следующие методы решения:
1) Метод подстановки (подробно не рассматриваем из-за его простоты и известности)
Метод вспомогательного неизвестного, когда одно из уравнений
системы содержит слагаемые одного, но видоизмененного типа.
Например, 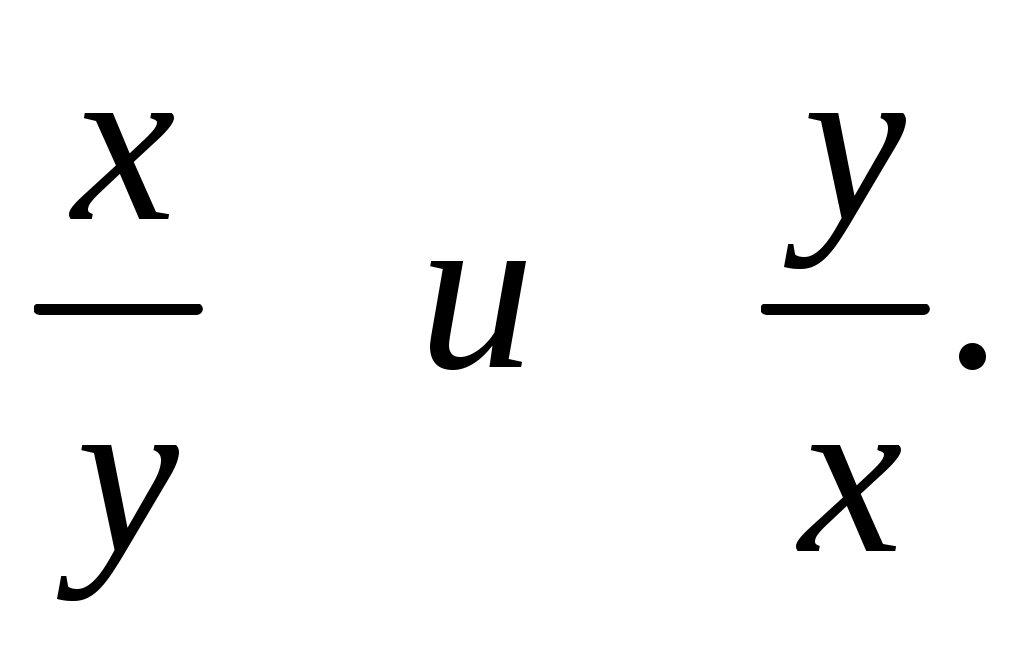 Тогда, можно Тогда, можно  и решить уравнение с одним неизвестным t, а затем результат этого решения использовать, продолжая решать систему. и решить уравнение с одним неизвестным t, а затем результат этого решения использовать, продолжая решать систему.
Пример 32.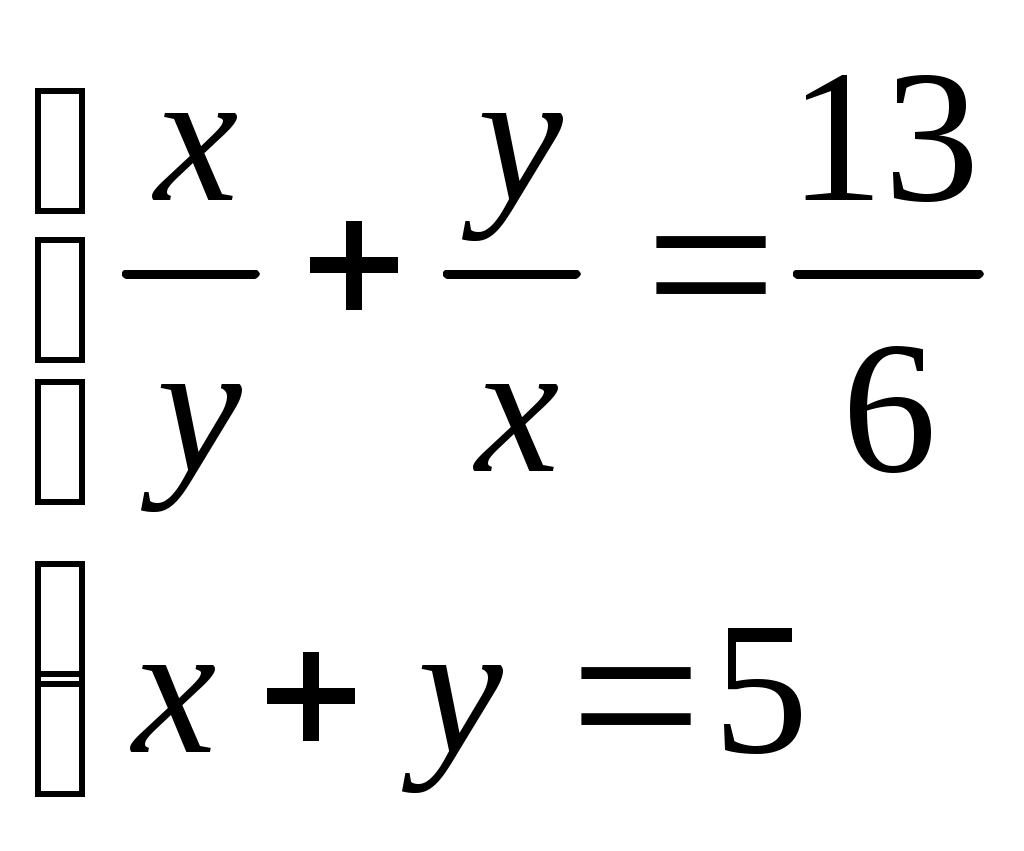
Сделаем замену  ; Тогда первое уравнение системы примет вид ; Тогда первое уравнение системы примет вид  Решаем квадратное уравнение Решаем квадратное уравнение 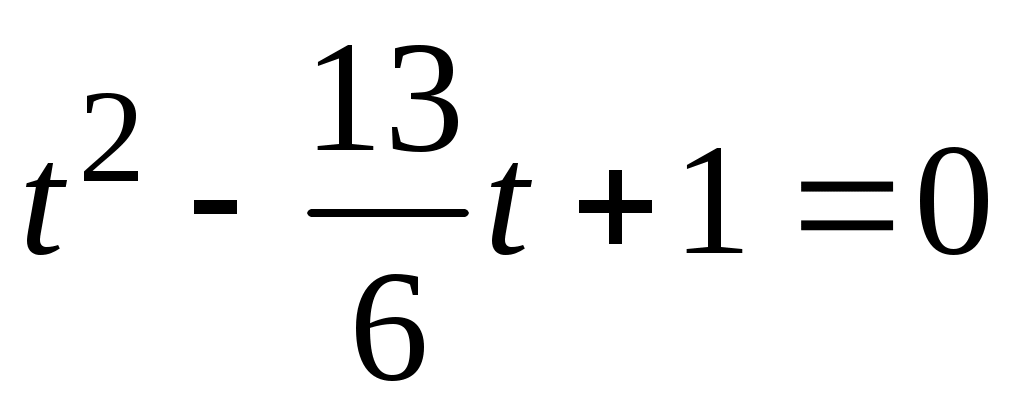 и получаем и получаем 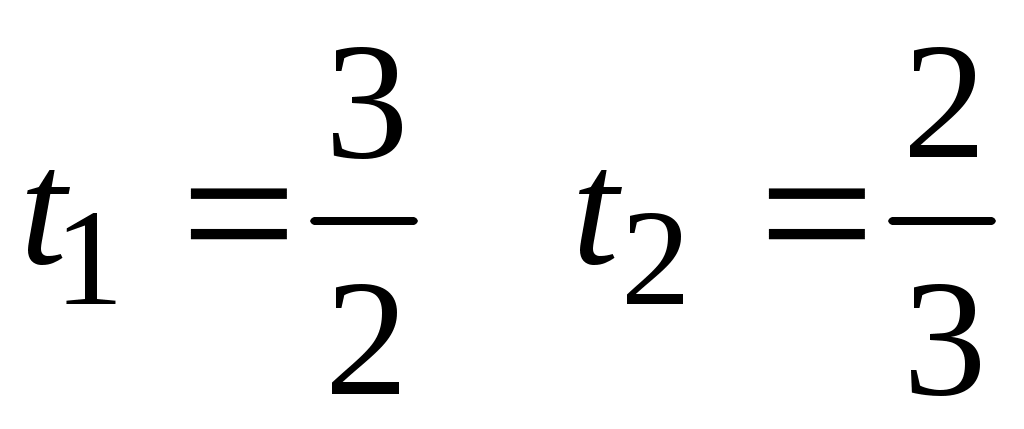 , то есть , то есть
а) 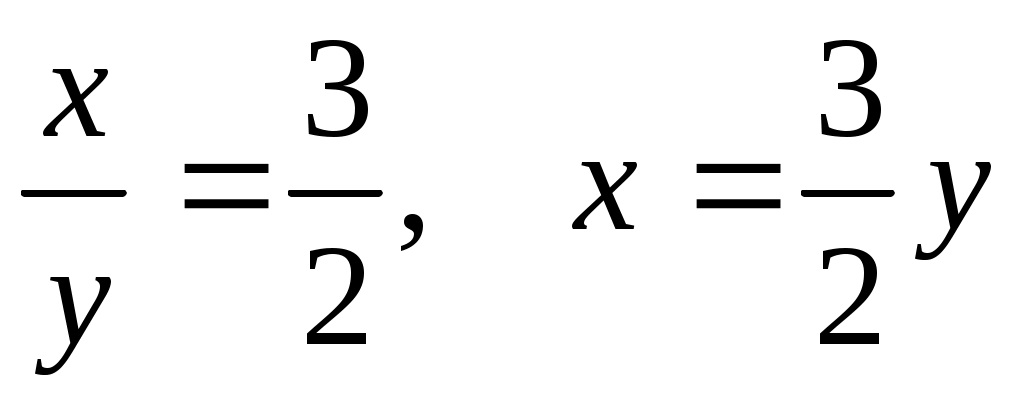 и второе уравнение системы будет иметь вид и второе уравнение системы будет иметь вид
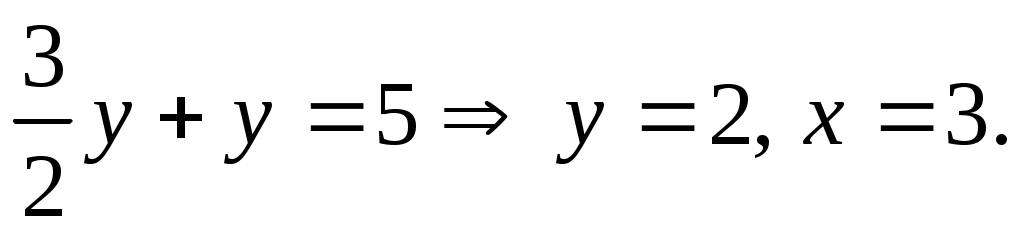
б) 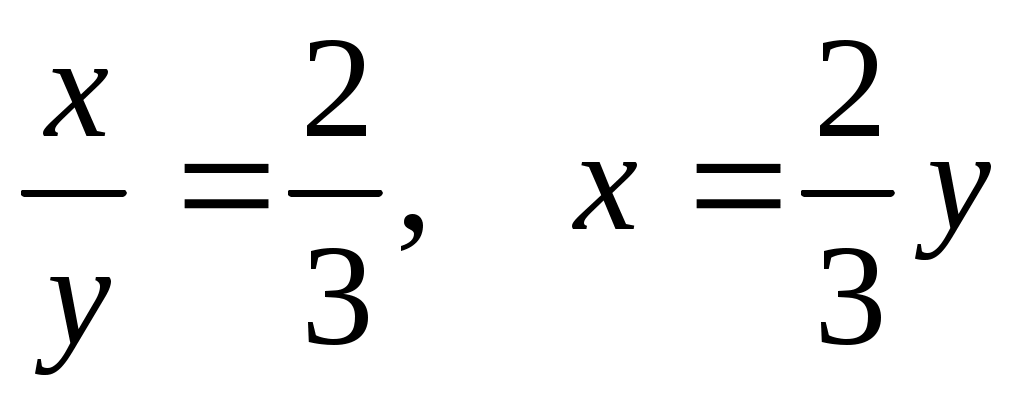 . Второе уравнение системы определит . Второе уравнение системы определит 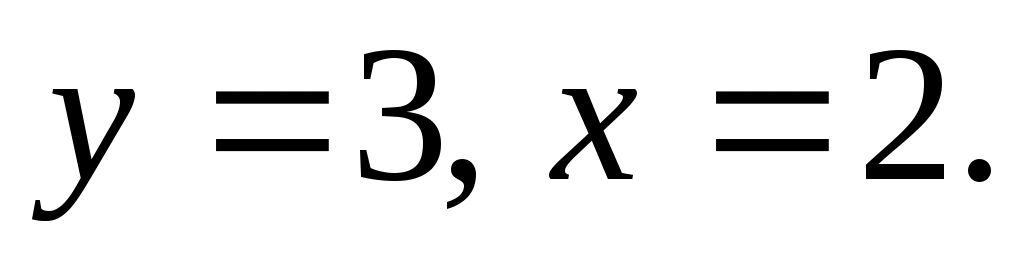
Алгебраические преобразования системы (наиболее сложный
метод), основанные на формулах сокращенного умножения, и
алгебраических действиях над левыми и правыми частями
уравнений системы.
Пример 33. 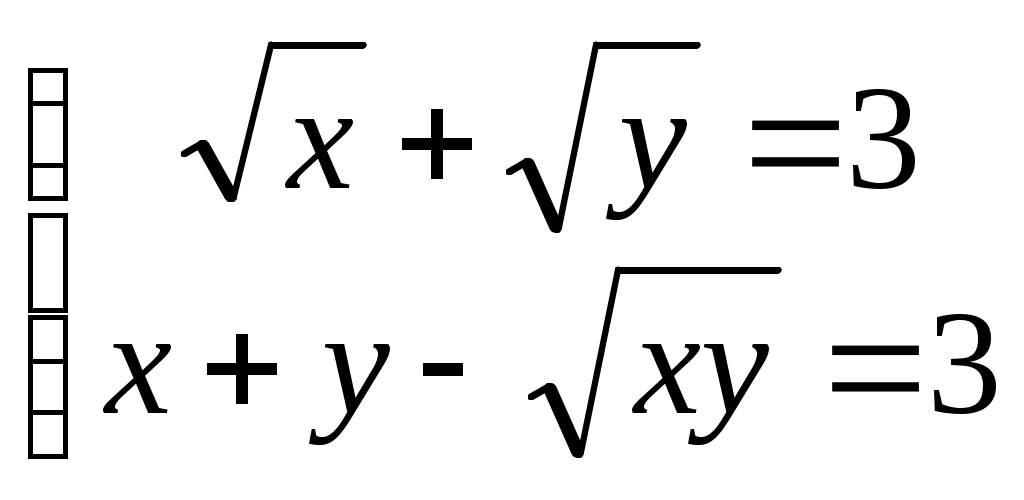
Учтем, что 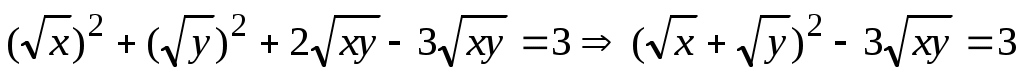 . .
Тогда 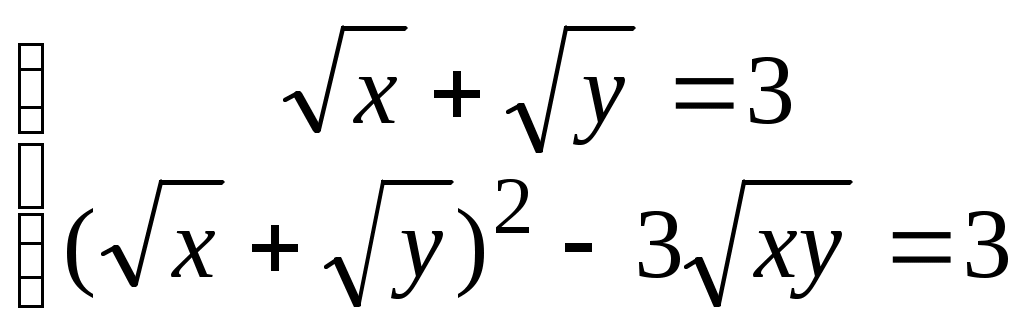
Используя равенство 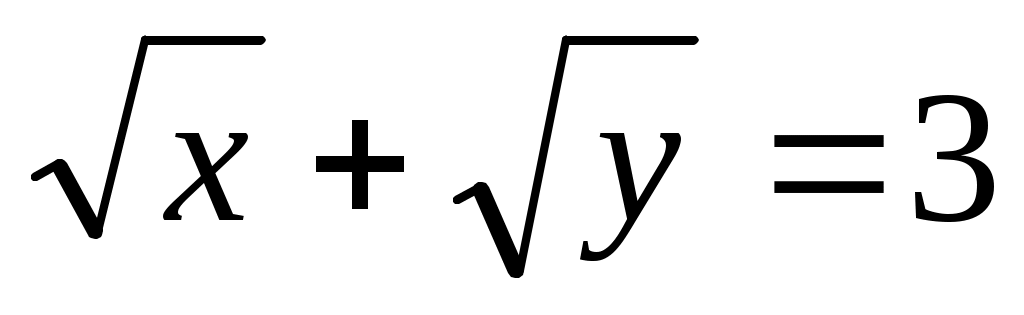 , получим второе уравнение системы в виде , получим второе уравнение системы в виде 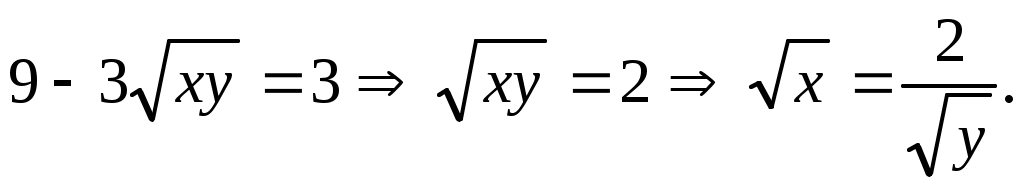 Получена зависимость между Получена зависимость между 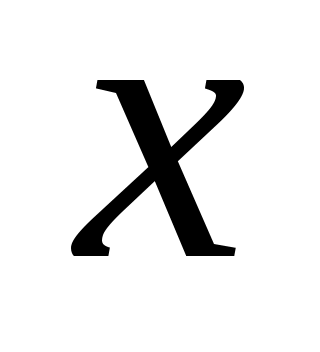 и и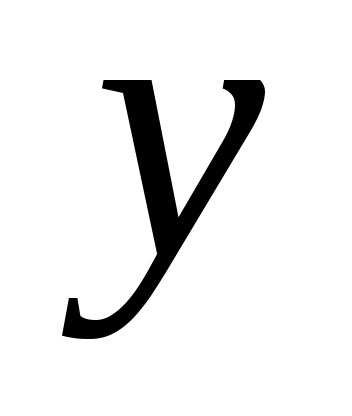 , и ее можно использовать для дальнейшего решения первого уравнения системы: , и ее можно использовать для дальнейшего решения первого уравнения системы: 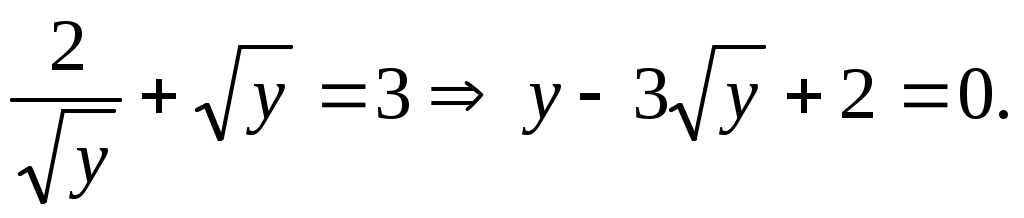 Заменим Заменим 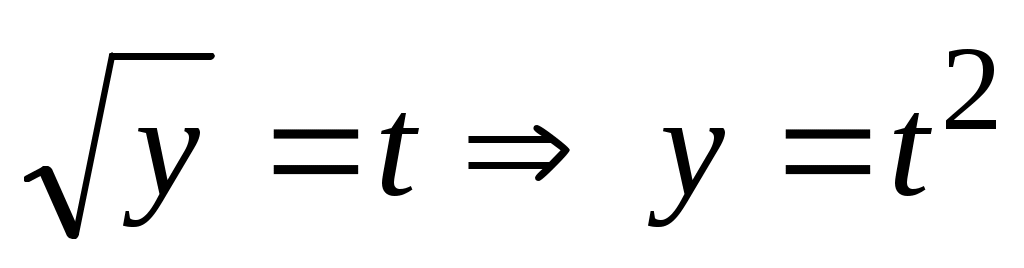 и решим квадратное уравнение и решим квадратное уравнение 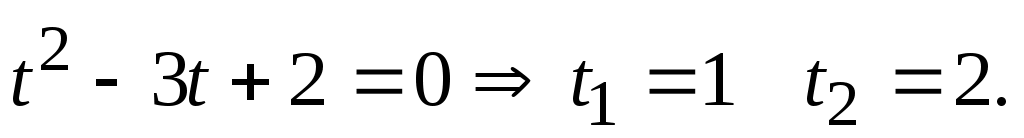 Далее, Далее,
а) 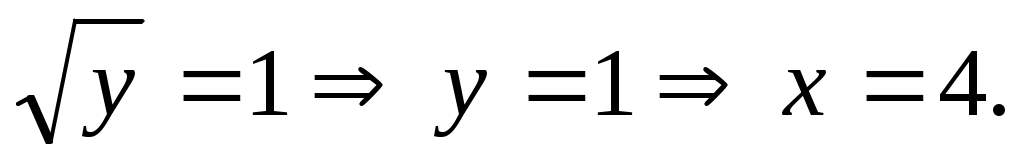
б) 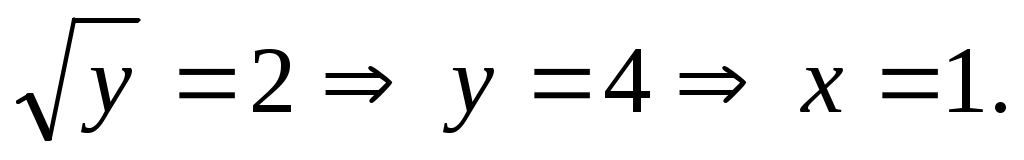
Пример 34. 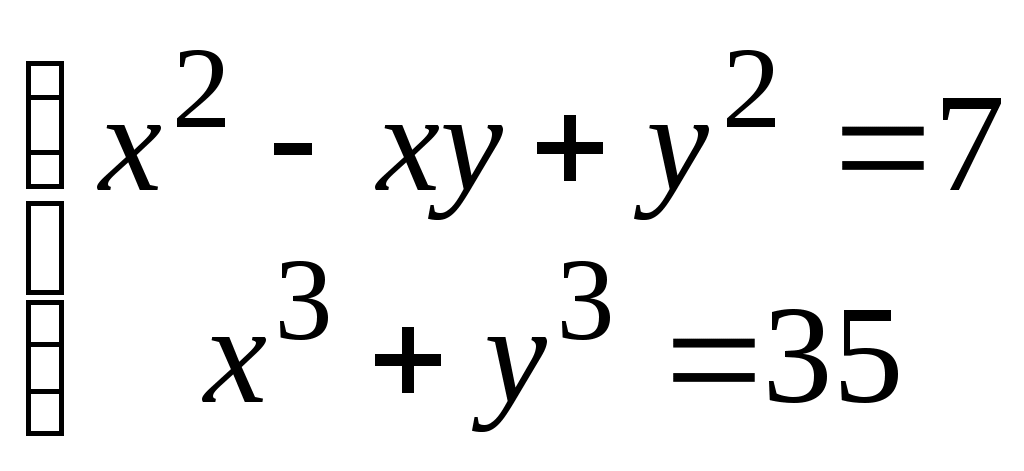
Заметим, что 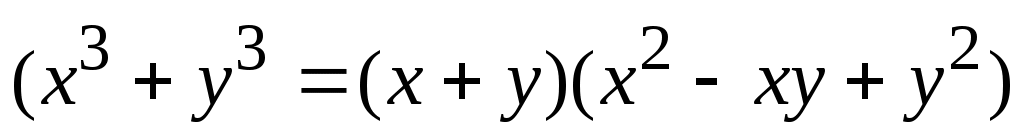 . Значит, можно использовать первое уравнение для второго, которое, в этом случае, будет иметь вид . Значит, можно использовать первое уравнение для второго, которое, в этом случае, будет иметь вид
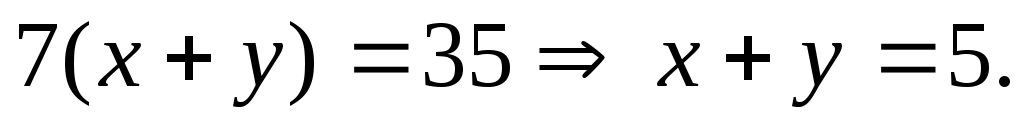 Получена зависимость между Получена зависимость между 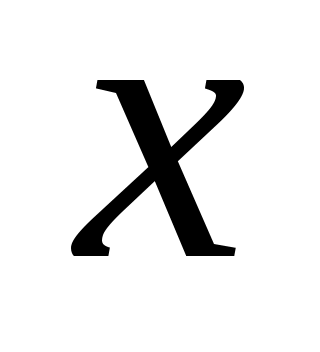 и и 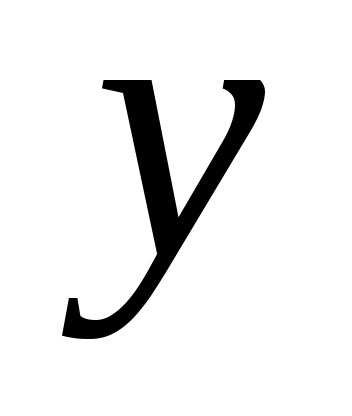 , которую можно использовать для решения первого уравнения, как уравнения с одним неизвестным. , которую можно использовать для решения первого уравнения, как уравнения с одним неизвестным.
Пример 35. 
Преобразуем первое уравнение: 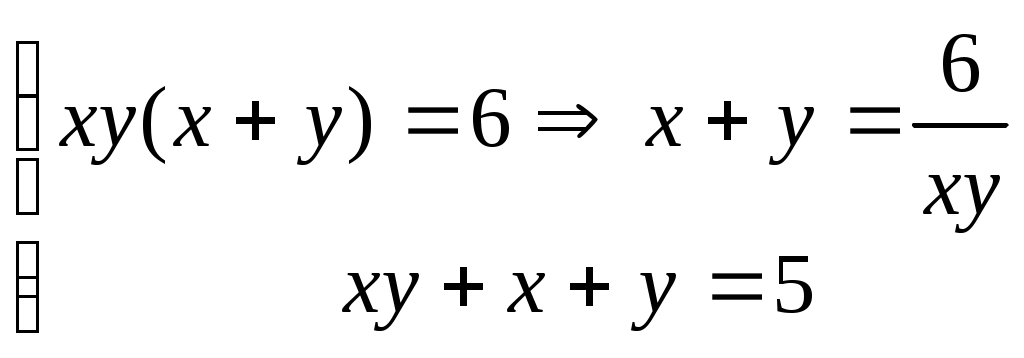
Второе уравнение примет вид 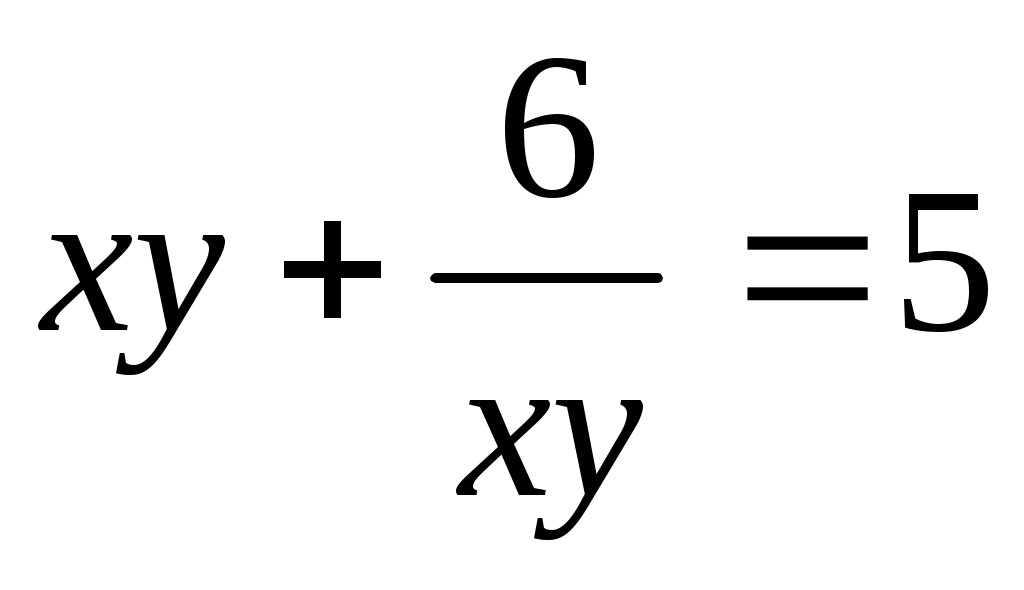 . Если . Если 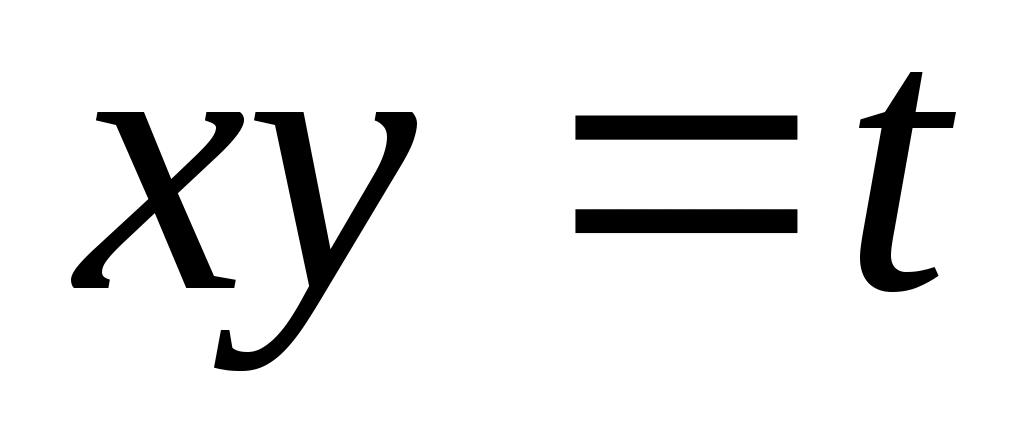 , то , то 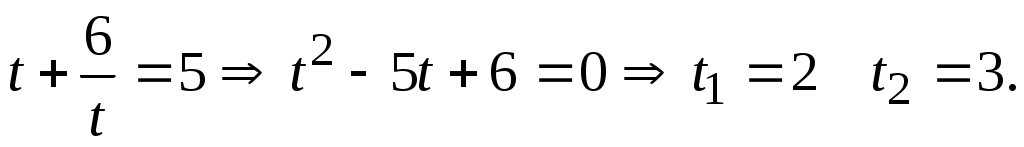 Получены зависимости между Получены зависимости между
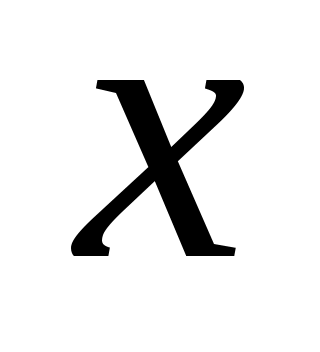 и и 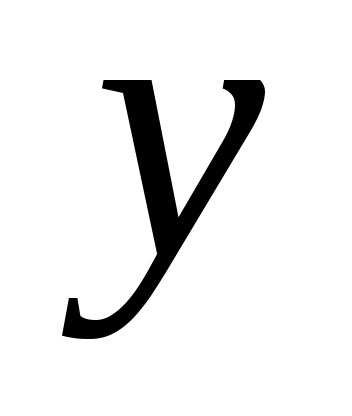 : а) : а) 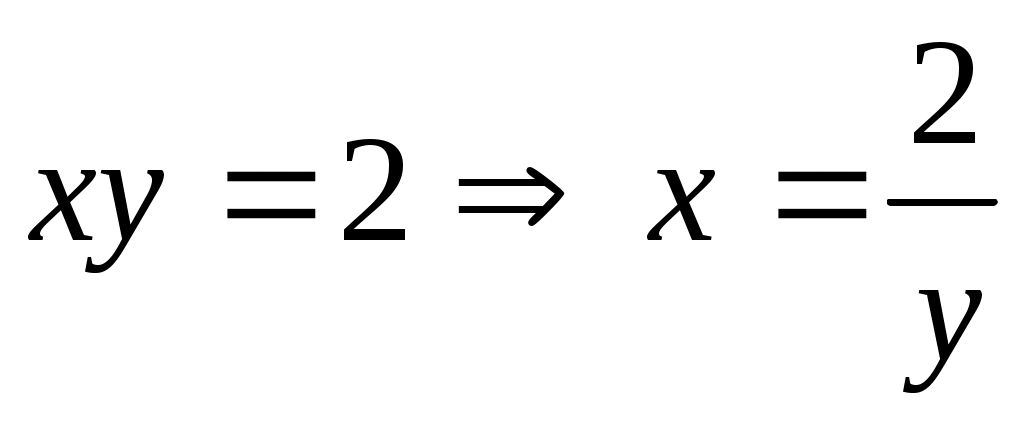 б) б)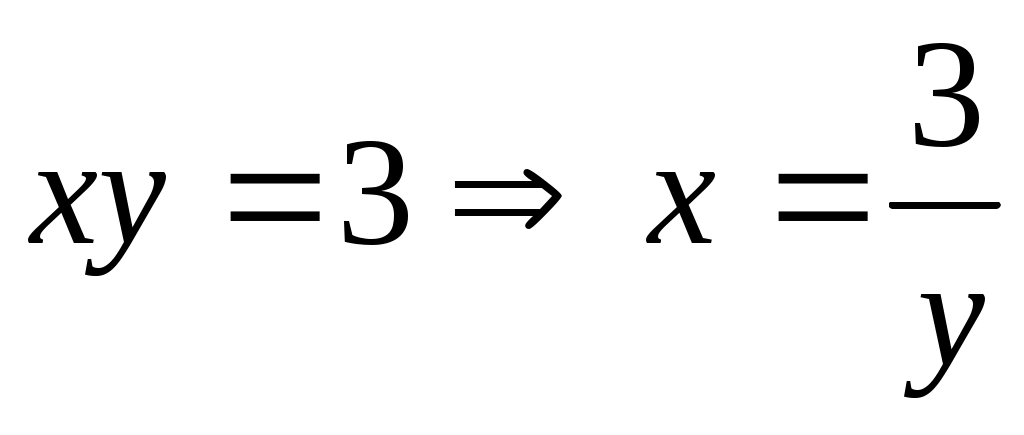 . Случай (б) не приводит к решению квадратного уравнения и не определяет решения системы. . Случай (б) не приводит к решению квадратного уравнения и не определяет решения системы.
§11. Решение иррациональных уравнений и неравенств
При решении иррациональных уравнений необходимо: полученное решение проверить подстановкой в исходное уравнение, так как при решении равносильность уравнений часто нарушается.
Способ решения уравнения зависит от его вида, и можно рекомендовать следующие действия:
Если уравнение содержит только одно выражение с неизвестным
под знаком радикала (корня), то его уединяют в определенной
части уравнения и возводят обе части уравнения в степень корня,
избавляясь от иррациональности.
Таким способом решается задача 13 блока 3.
Если один и тот же радикал встречается в разных частях уравнения, то рациональному решению помогает правильная компоновка уравнения.
Пример. 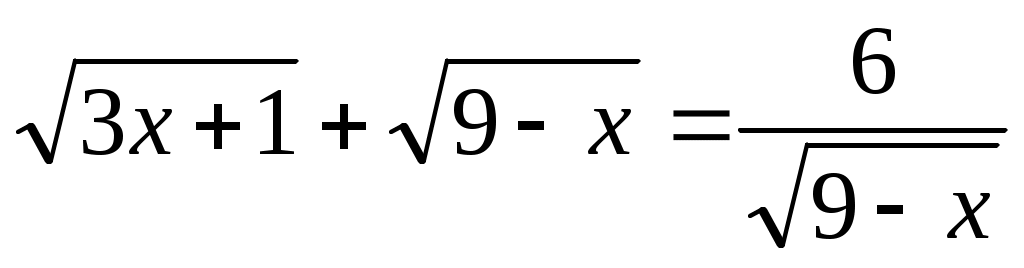 (задача 14 блока 3) (задача 14 блока 3)
Преобразования: 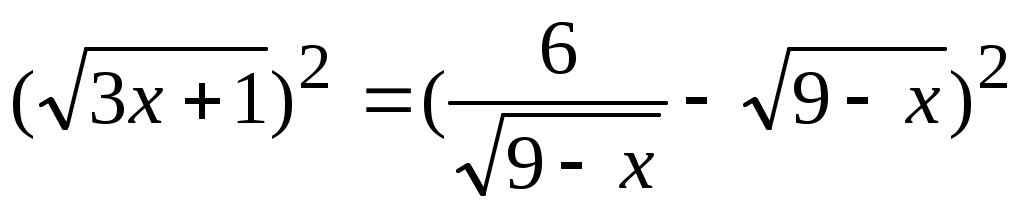 . .
При повторении некоторой части выражения, стоящего под знаком корня и без него, можно сделать замену переменной.
Пример 36. 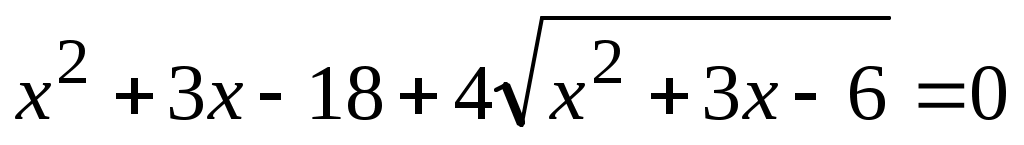
Замена: 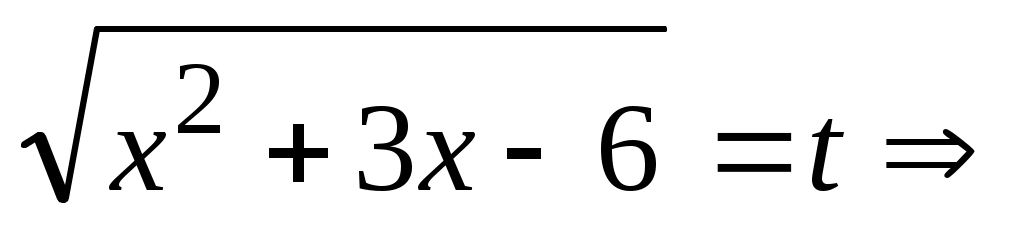 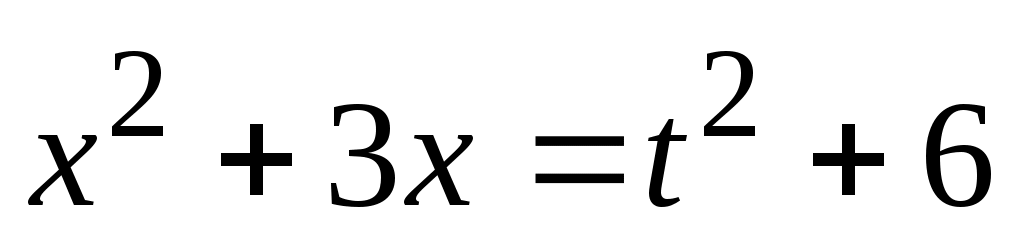
Уравнение преобразуется к виду: 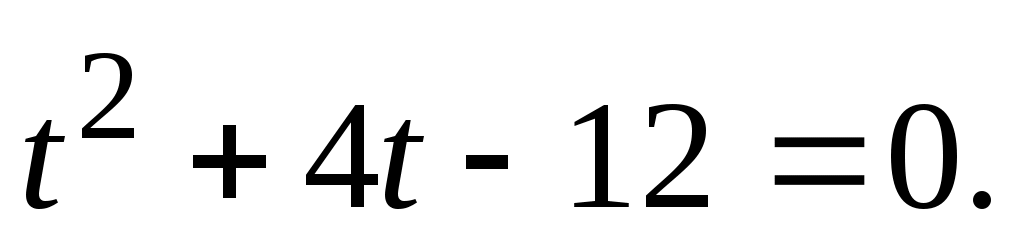
Получив значения 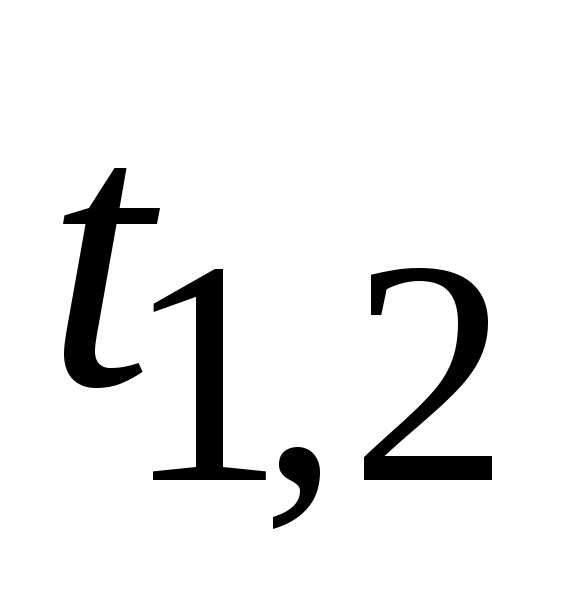 , приравниваем этим значениям выражение , приравниваем этим значениям выражение 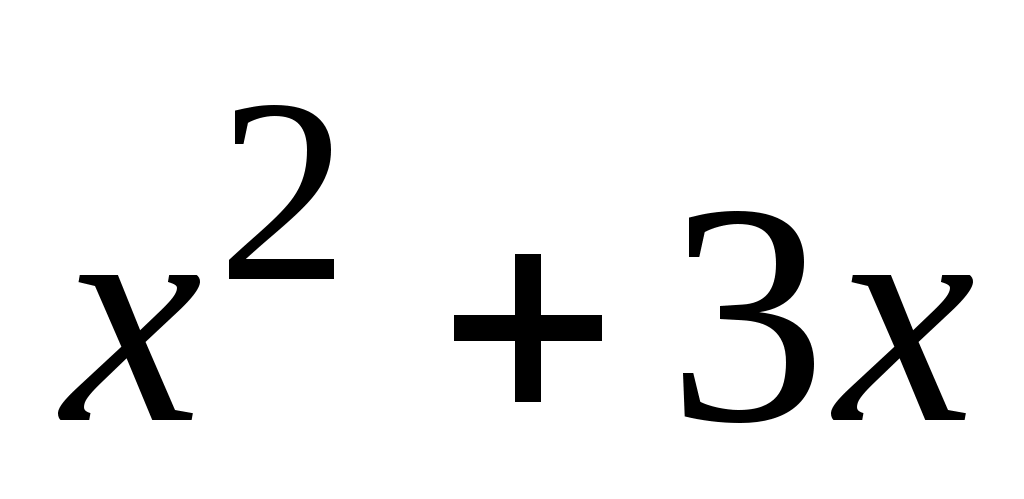 и получаем решения; проверяем их подстановкой в исходное уравнение. и получаем решения; проверяем их подстановкой в исходное уравнение.
4) При решении уравнения вида
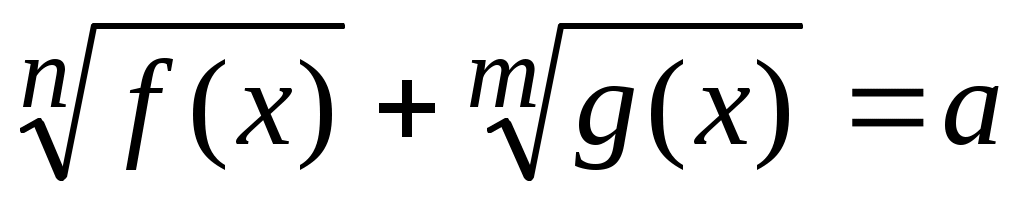 , где , где 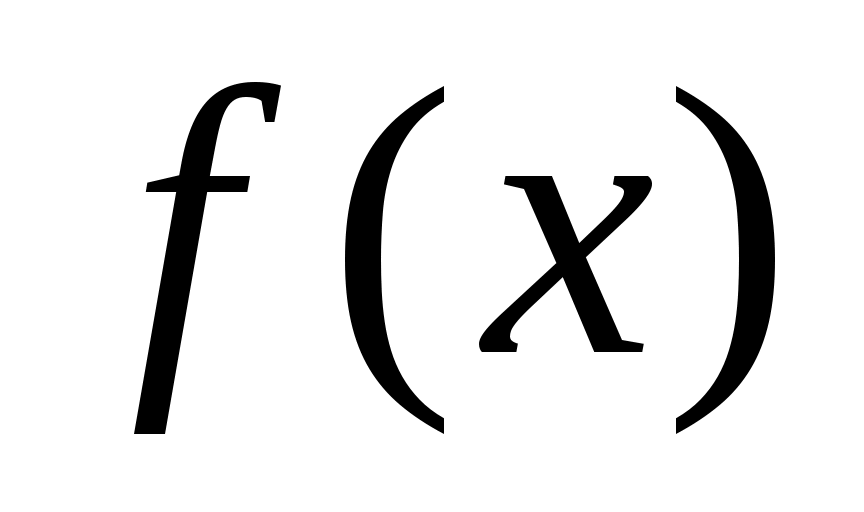 и и 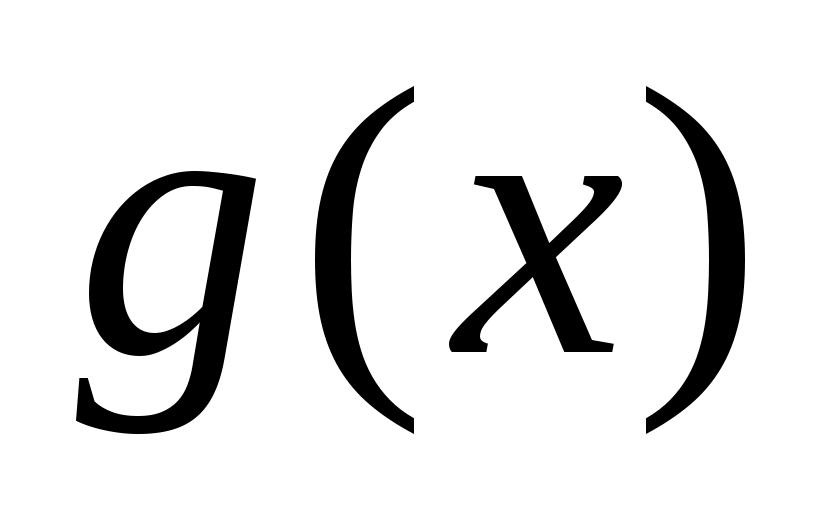 линейные функции вида линейные функции вида 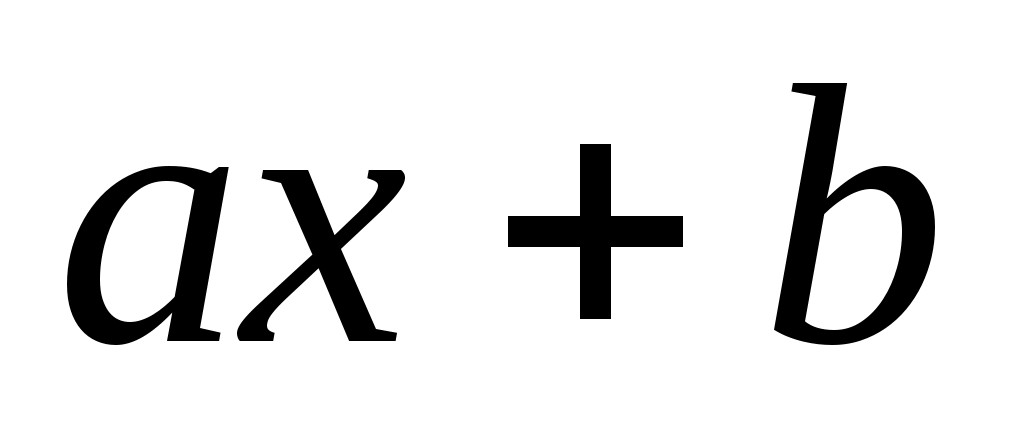
можно ввести новые переменные и решить систему нелинейных уравнений. Рассмотрим описанные действия на примере.
Пример 37. 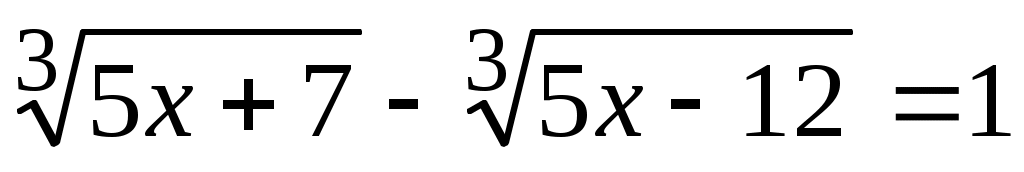 . .
Замена:  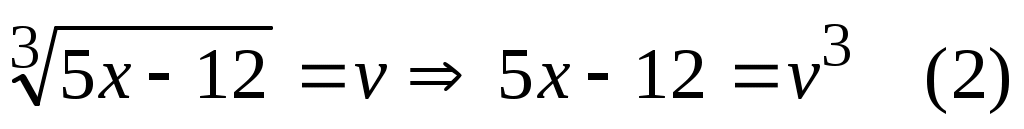
(1)-(2)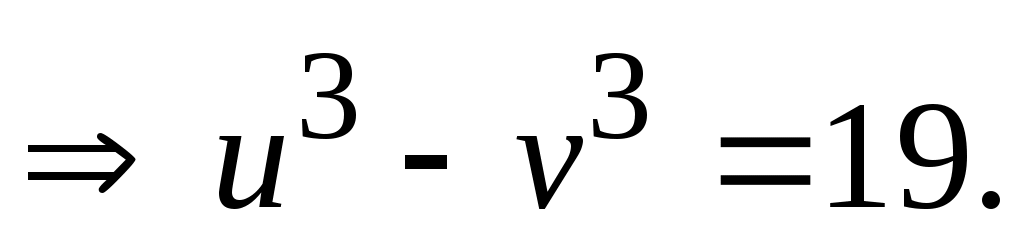 Если коэффициенты при Если коэффициенты при 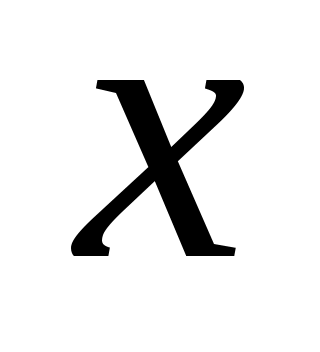 в (1) и (2) неодинаковы, то, прежде, чем складывать или вычитать (1) и (2), нужно уравнять эти в (1) и (2) неодинаковы, то, прежде, чем складывать или вычитать (1) и (2), нужно уравнять эти
коэффициенты домножением на соответствующие множители (1) и (2).
С учетом исходного уравнения, нелинейная система будет иметь вид
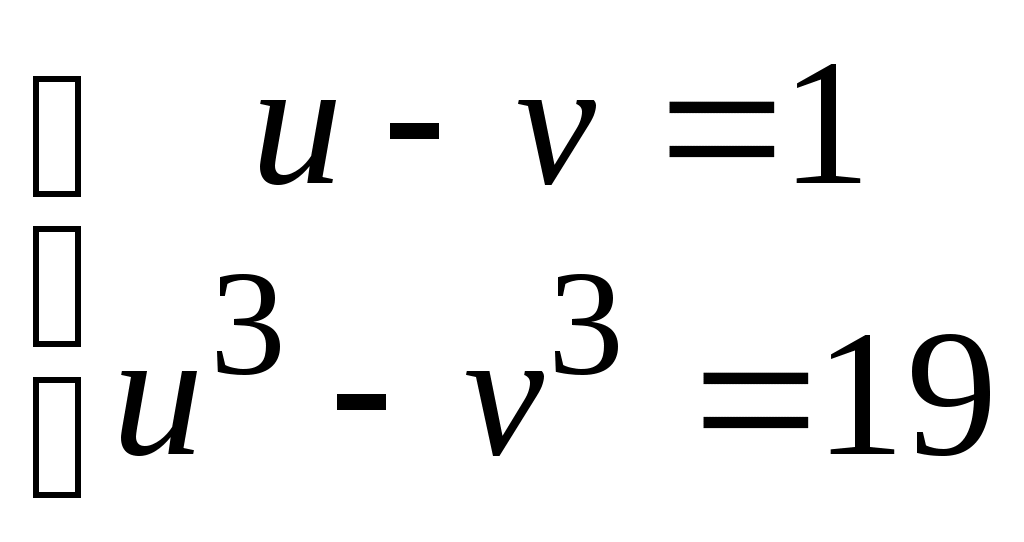
Используя метод подстановки 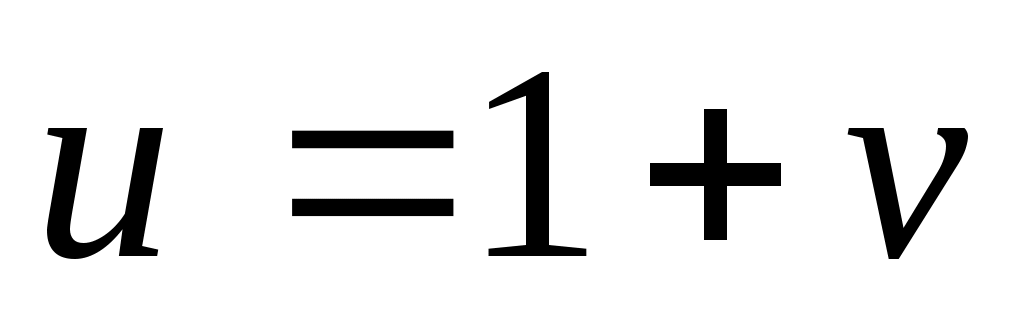 , решим второе уравнение системы: , решим второе уравнение системы: 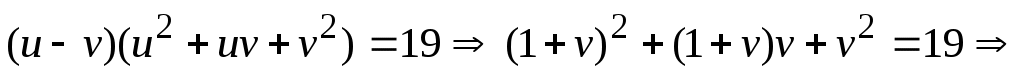
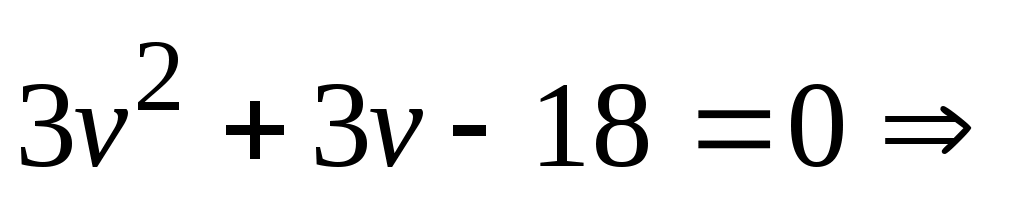 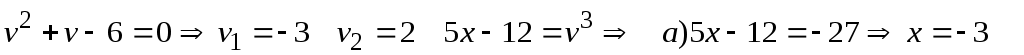 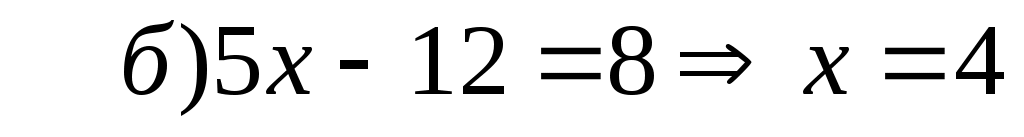 . .
При решении иррациональных неравенств очень внимательно нужно отнестись к тем, которые содержат радикалы четной степени. Неравенство нельзя возводить в четную степень, если хотя бы одна из его частей отрицательна.
Существуют два основных вида неравенств, к которым сводятся многие другие:
1)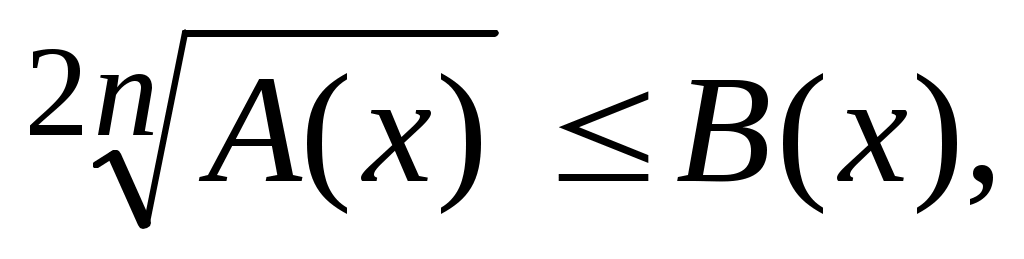 (пусть n=1) (пусть n=1) 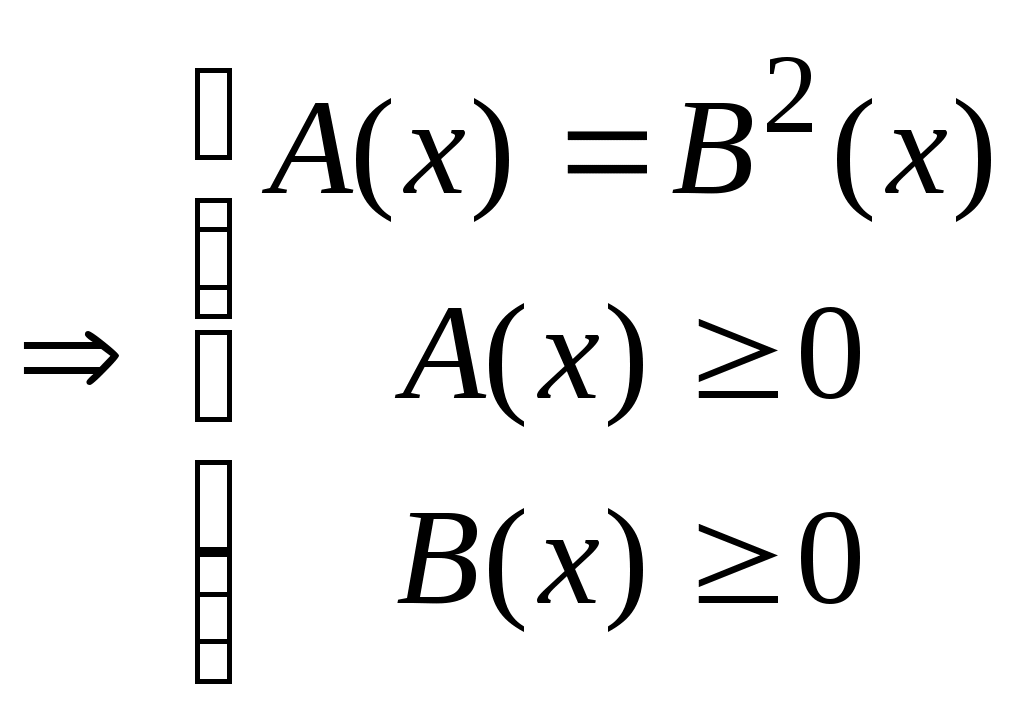
2)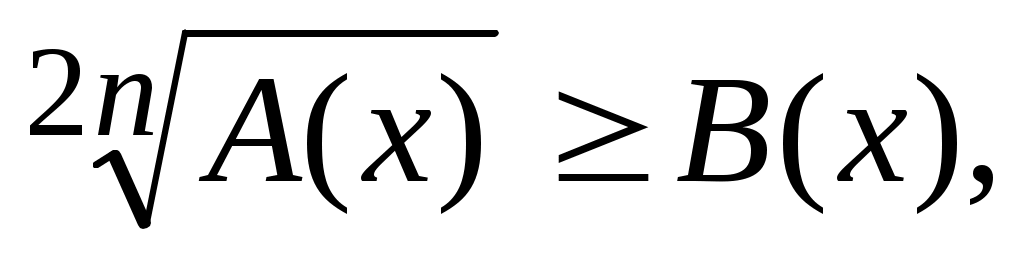 (пусть n=1).Неравенство распадается на две системы (пусть n=1).Неравенство распадается на две системы
неравенств:
а)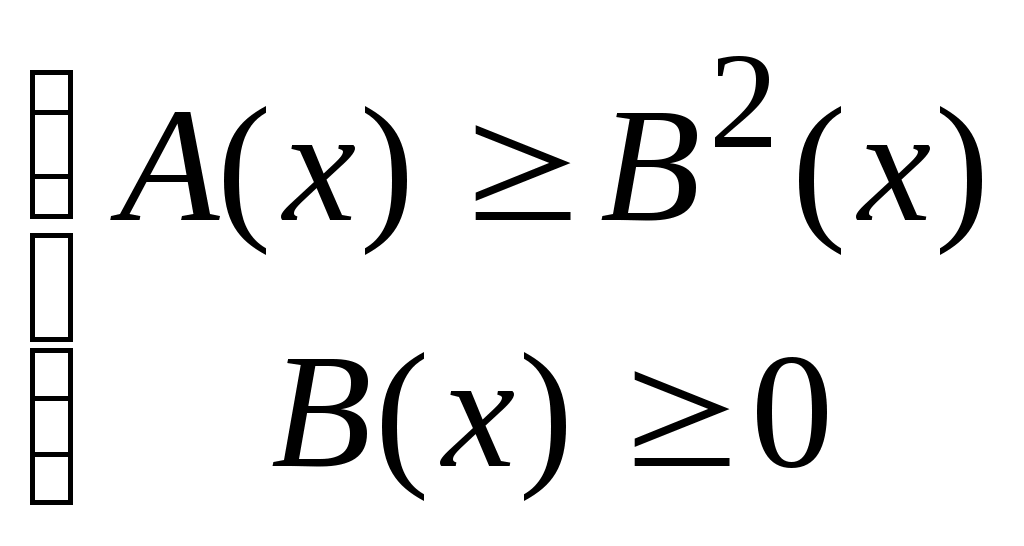 б) б)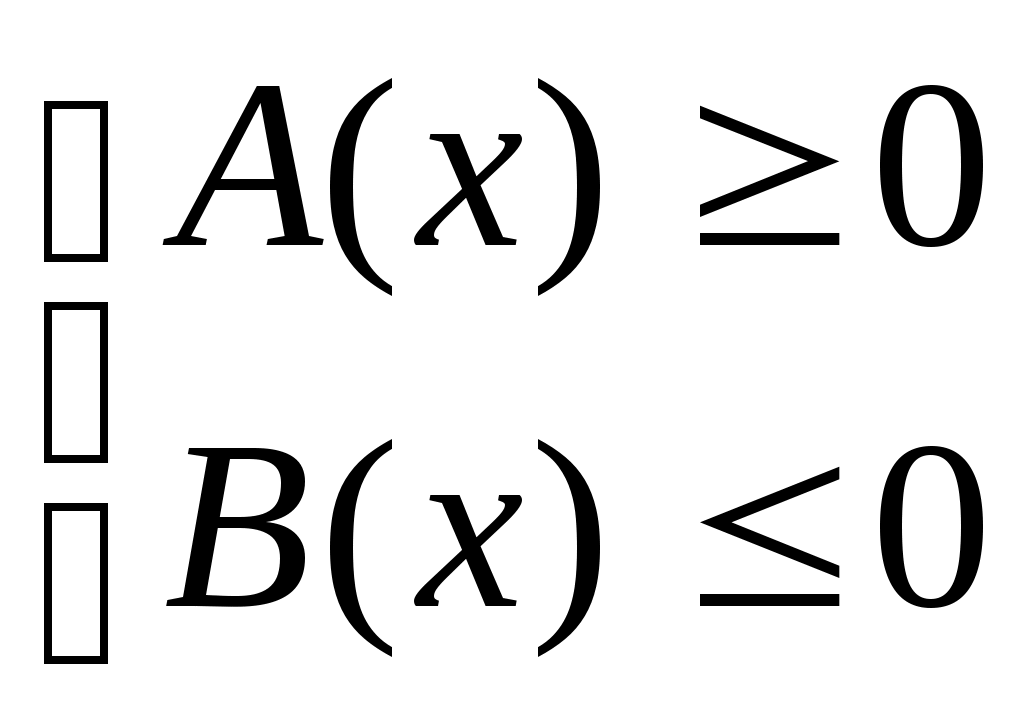
При решении иррациональных неравенств используются те же методы решения, что и для рациональных неравенств.
Пример 37.  1 1
а) Находим область определения: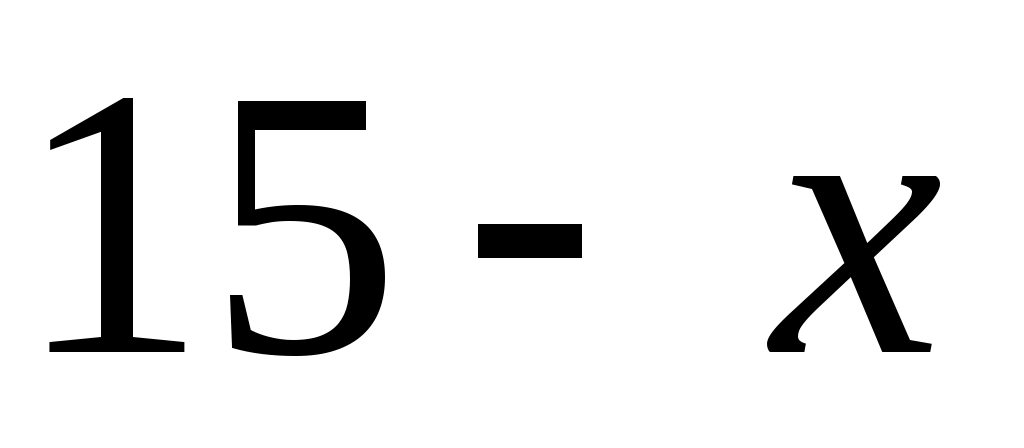 0; 0; 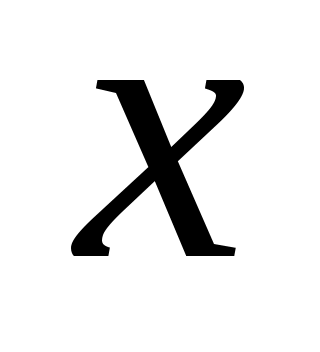 15. 15.
б) Переносим все слагаемые в левую часть, и приводим ее к общему знаменателю: 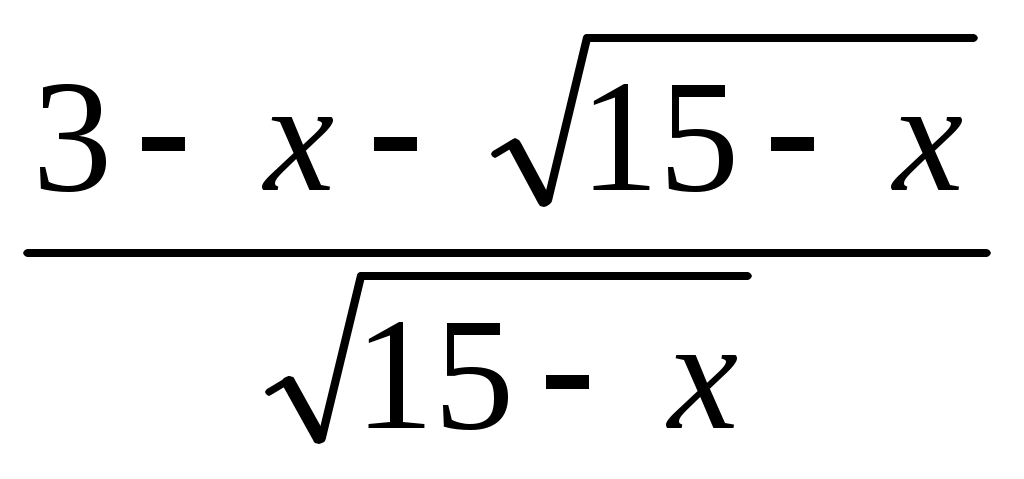 0 0
в) Для решения неравенства методом интервалов получим нулевые точки: 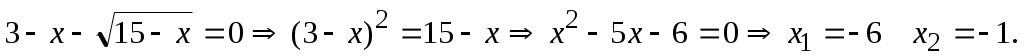
На интервале (-1;15) выражение 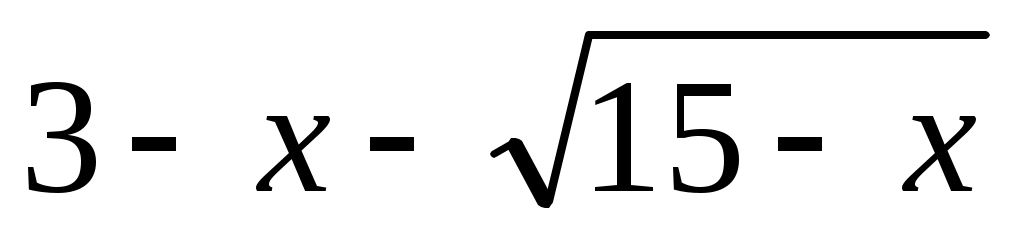 меньше нуля, поэтому решением неравенства является интервал меньше нуля, поэтому решением неравенства является интервал
(-1;15).
§12. Прогрессии
При решении задач, связанных с арифметической (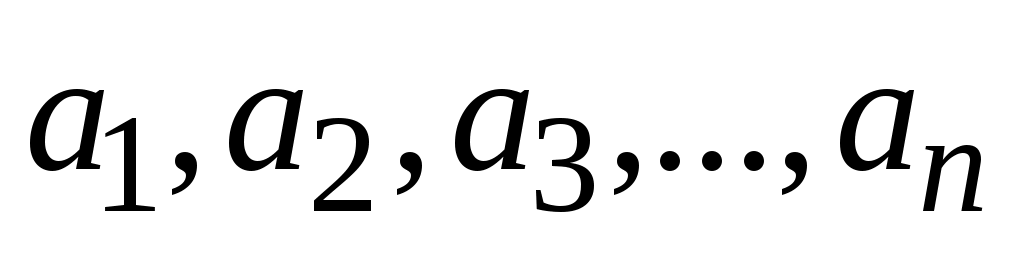 ) и геометрической ( ) и геометрической ( 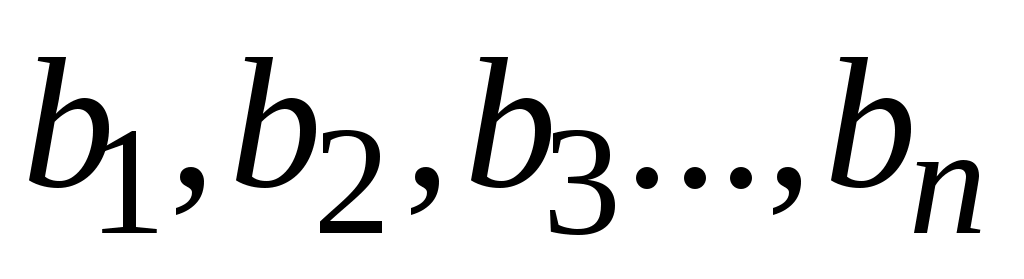 ) прогрессиями, где ) прогрессиями, где 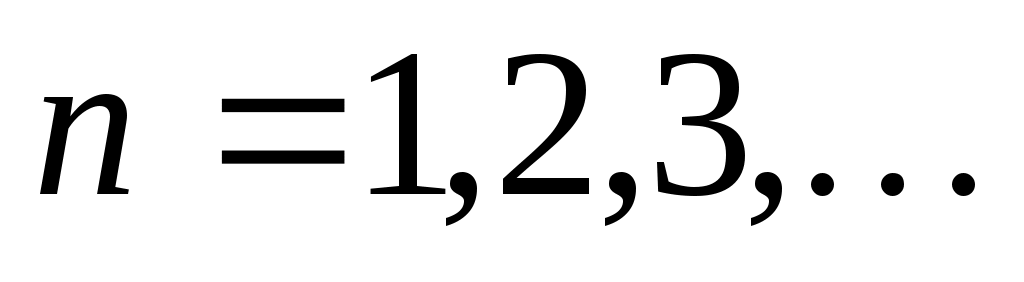 необходимо знать формулы: необходимо знать формулы:
1) 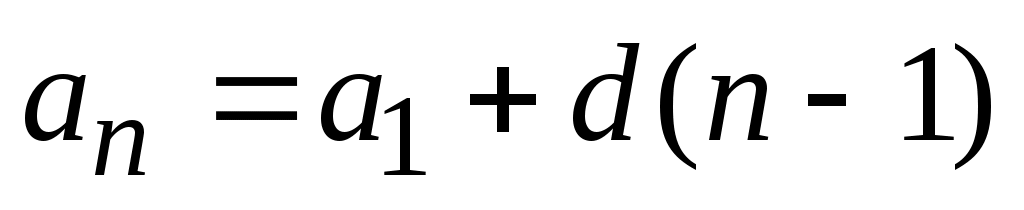 , где , где 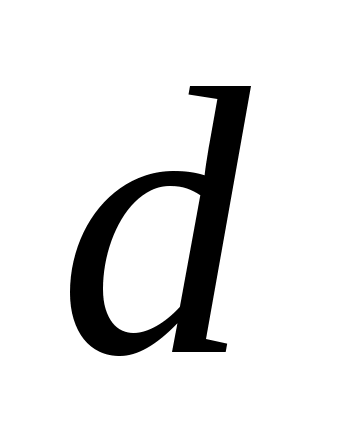 - разность арифметической прогрессии; - разность арифметической прогрессии;
2) 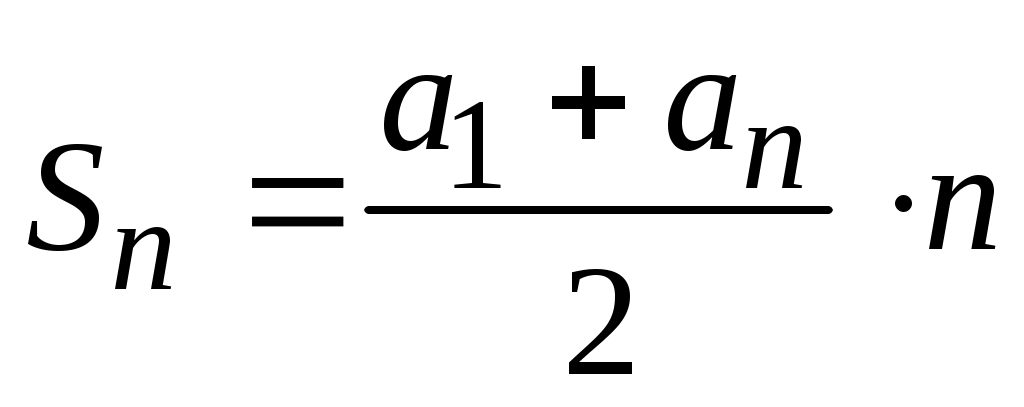 , ,
где 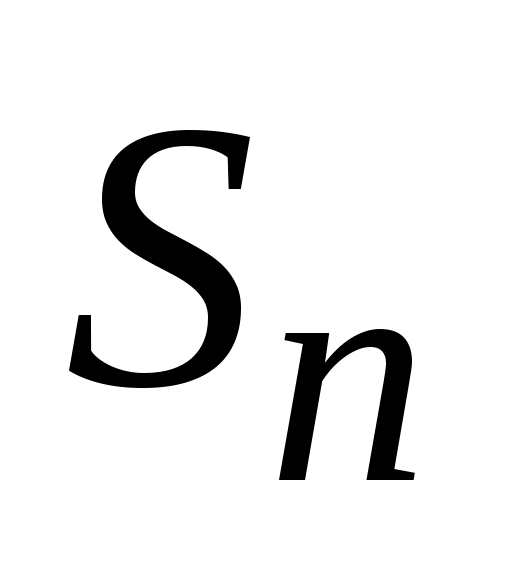 - сумма - сумма 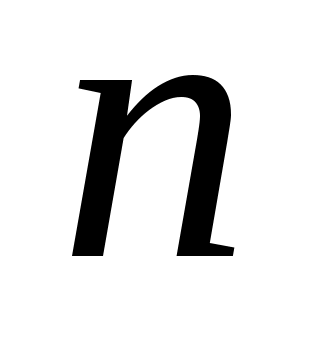 - членов арифметической прогрессии; - членов арифметической прогрессии;
3) 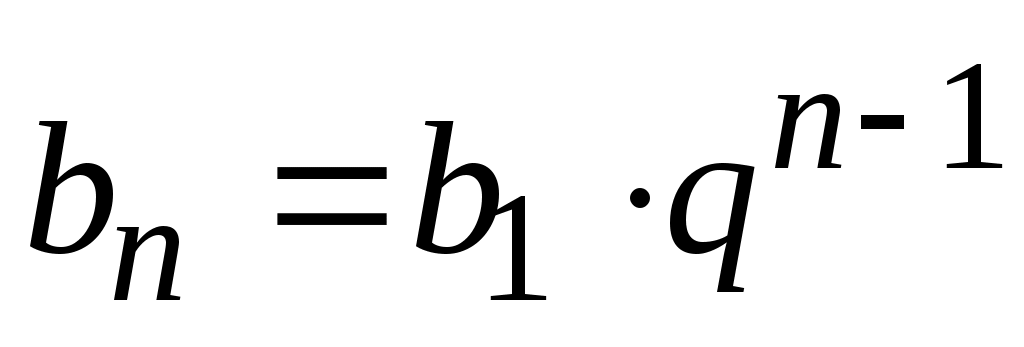 , где , где 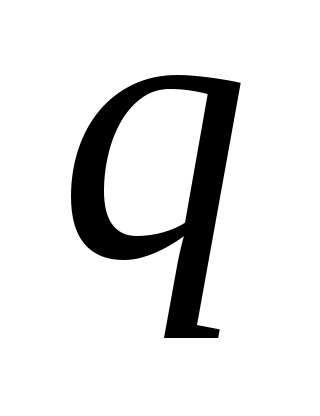 - знаменатель геометрической прогрессии; - знаменатель геометрической прогрессии;
4) 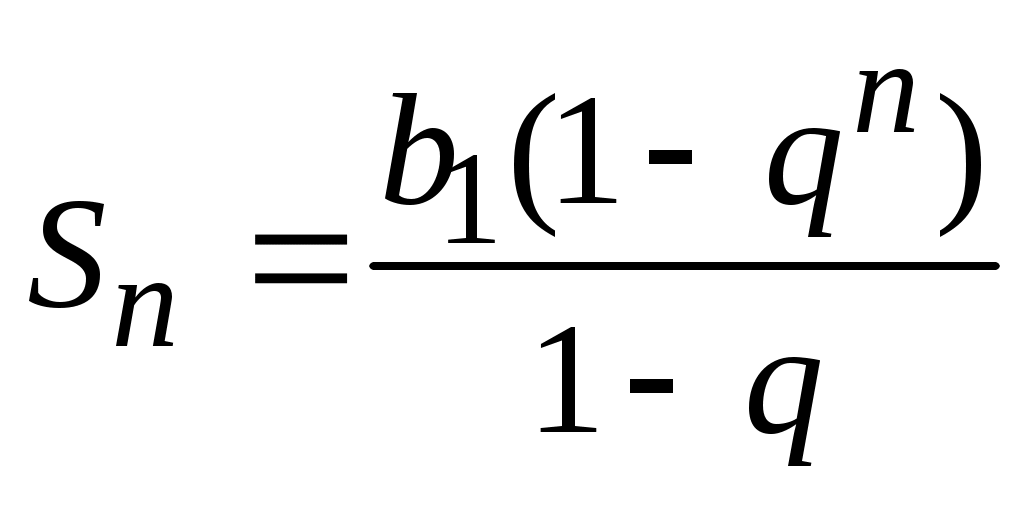 , ,
где 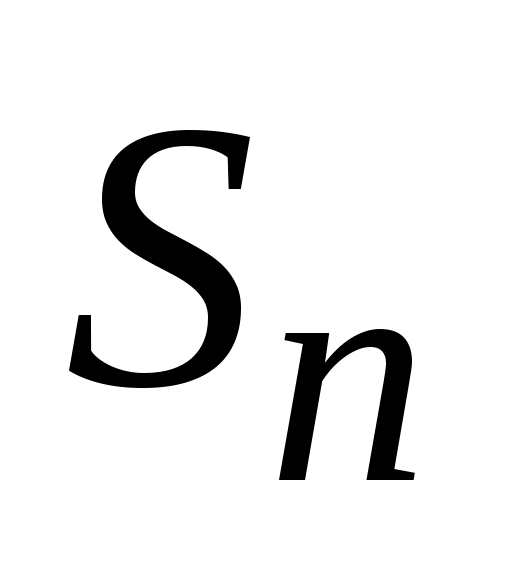 - сумма - сумма 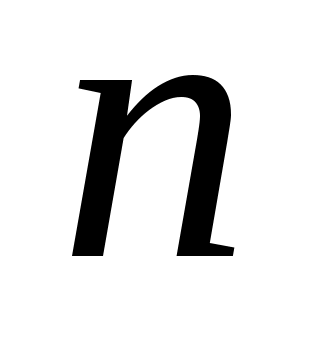 - членов геометрической прогрессии; - членов геометрической прогрессии;
5) 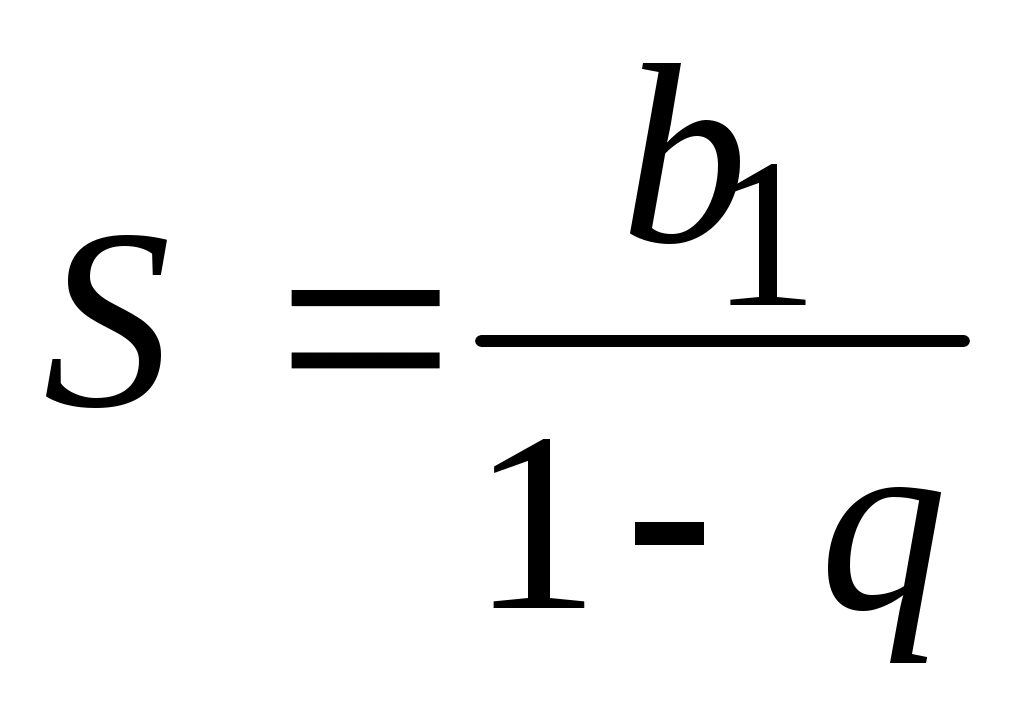 - сумма бесконечного числа членов убывающей - сумма бесконечного числа членов убывающей
геометрической прогрессии, для которой  1 и n. 1 и n.
Решение задач сводится к составлению системы уравнений, сложность которой зависит от условий задачи, и дальнейшему ее решению.
Пример 38. Три числа образуют убывающую арифметическую прогрессию, сумма которой равна 3. Известно, что сумма квадратов этих чисел равна 11. Найти разность прогрессии.
Представим условия задачи:
а) 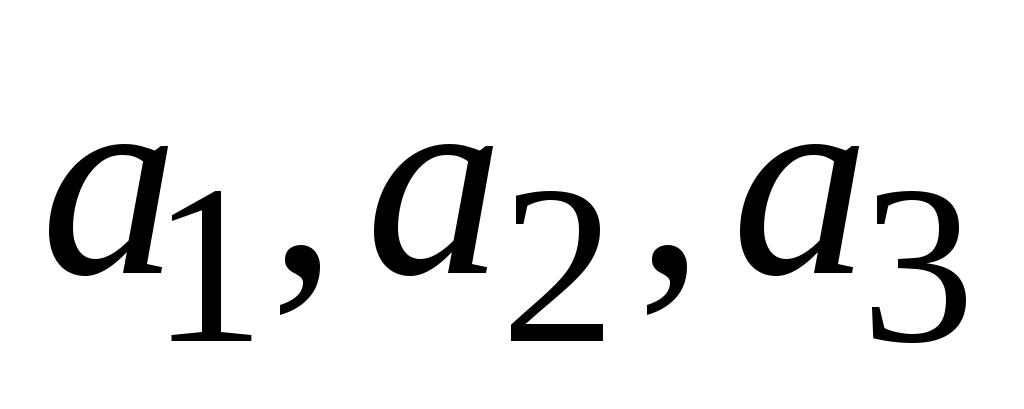 - 3 члена арифметической прогрессии; - 3 члена арифметической прогрессии;
б)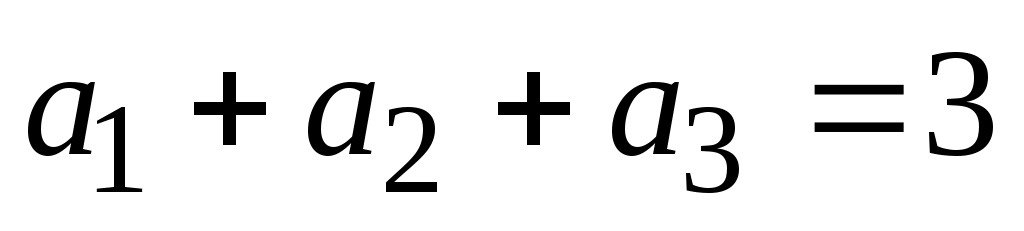 (по условию задачи: сумма членов прогрессии равна 3); (по условию задачи: сумма членов прогрессии равна 3);
в) 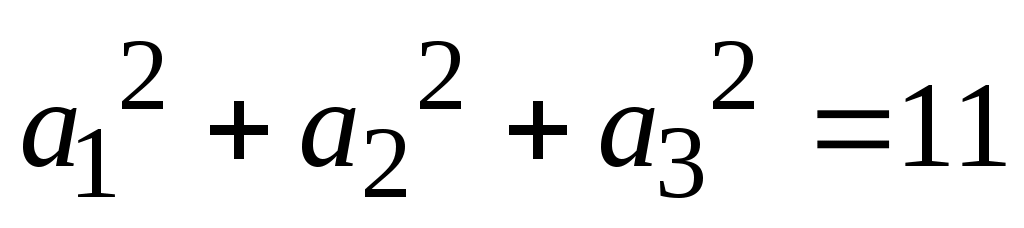 (по условию задачи: сумма квадратов членов (по условию задачи: сумма квадратов членов
прогрессии равна 11);
Получена нелинейная система уравнений: 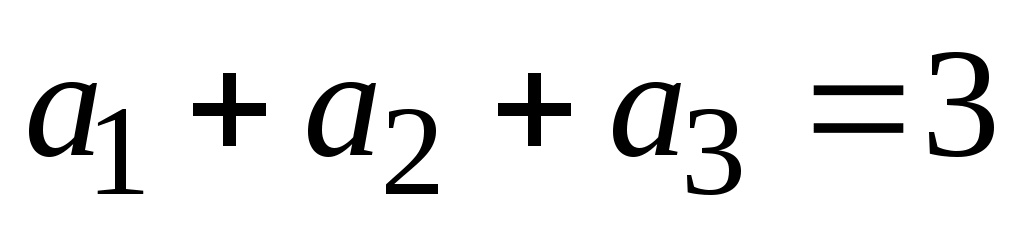
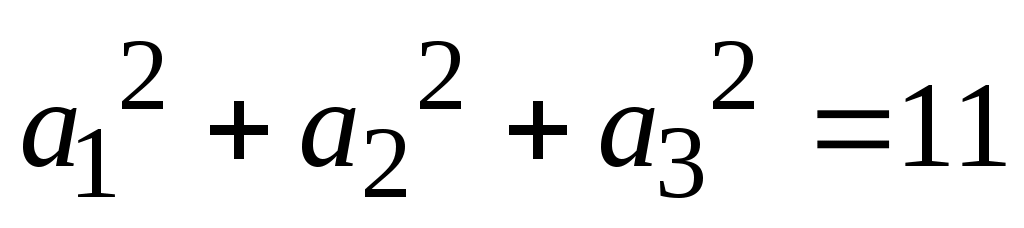 . .
Используем формулу 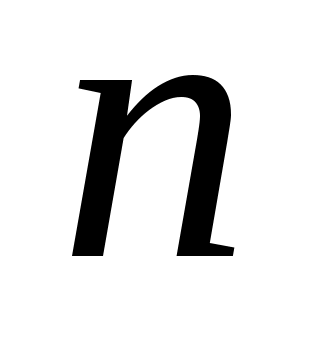 - члена арифметической прогрессии и определим: - члена арифметической прогрессии и определим: 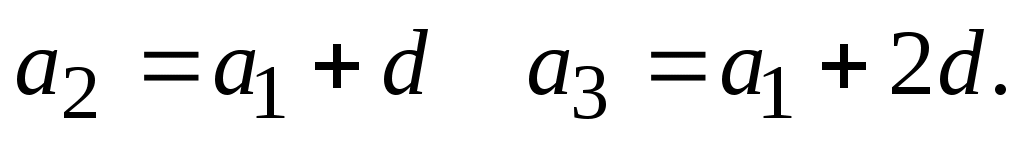 Тогда, система преобразуется к виду Тогда, система преобразуется к виду
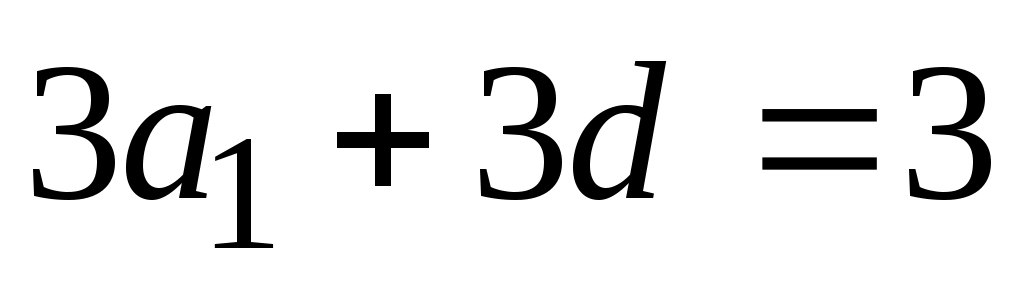
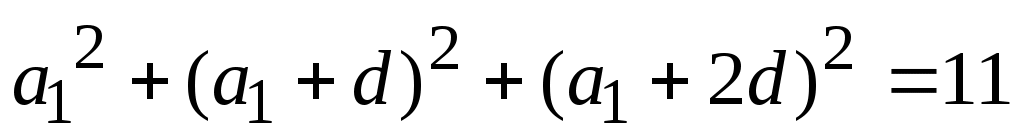 или или
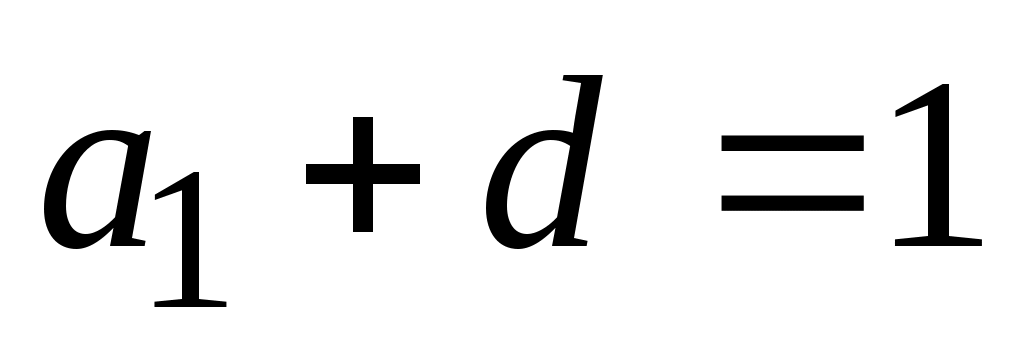
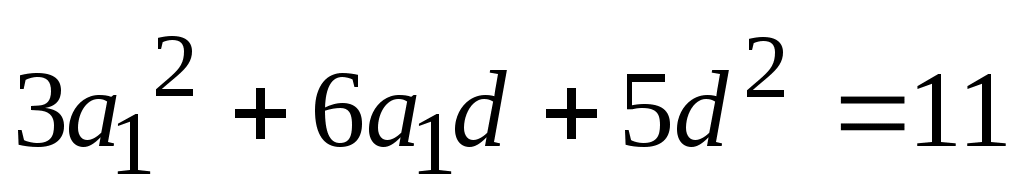
Сделаем подстановку 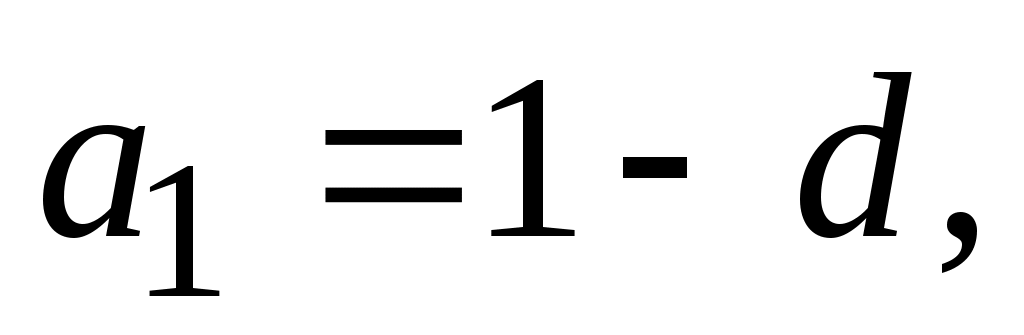 во второе уравнение системы, которое приобретет вид во второе уравнение системы, которое приобретет вид 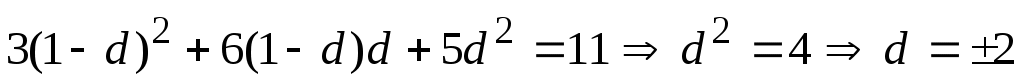
Так как, по условию задачи, прогрессия убывающая, то нужно взять значение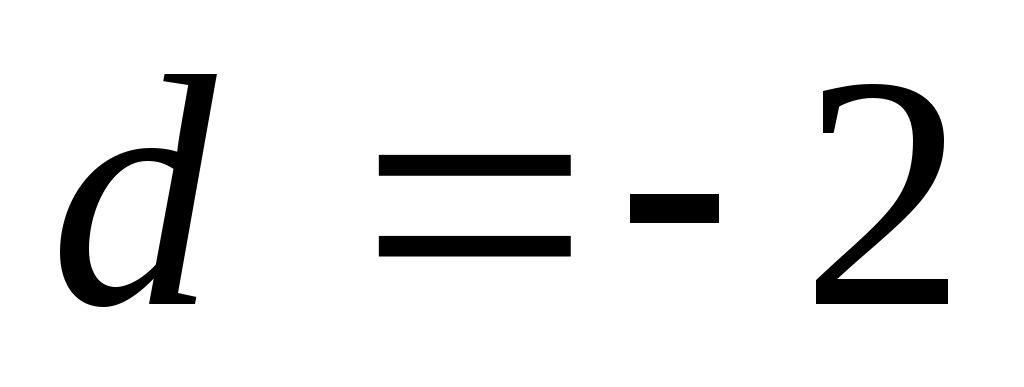 . .
Пример 39. Сумма первых двух членов бесконечно убывающей геометрической прогрессии равна 6, а отношение второго члена к пятому равно 8. Определить сумму прогрессии.
Представим условия задачи:
а) 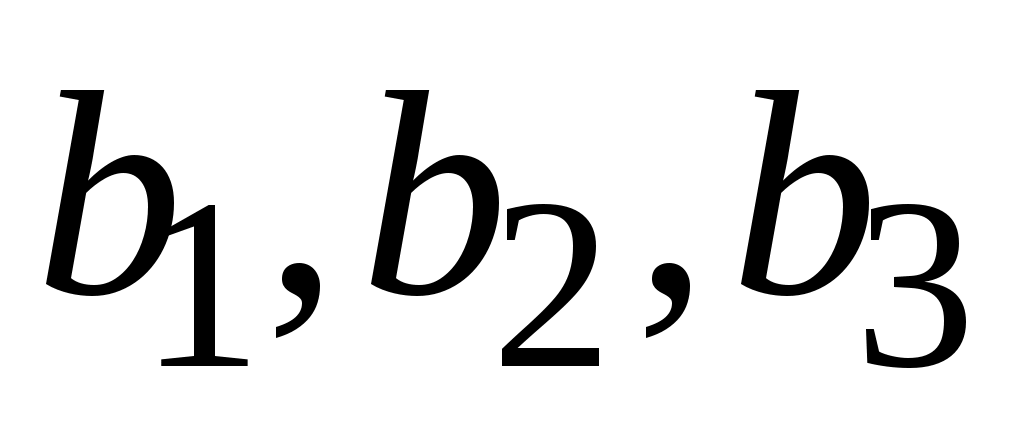 - 3 члена геометрической прогрессии; - 3 члена геометрической прогрессии;
б) 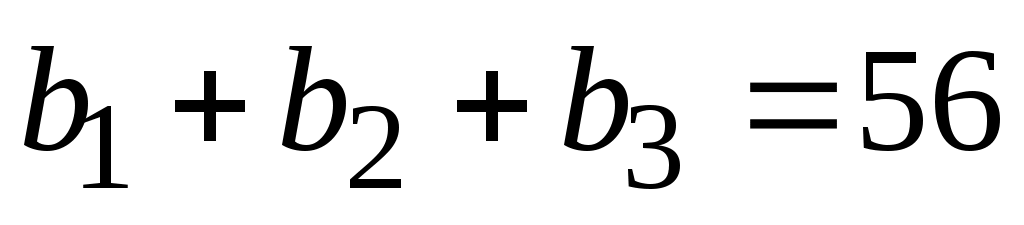 (по условию задачи: сумма 3-х членов геометрической (по условию задачи: сумма 3-х членов геометрической
прогрессии равна 56);
в) 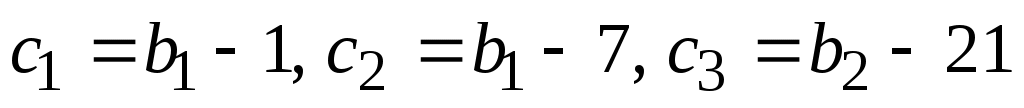 - три члена арифметической - три члена арифметической
прогрессии, то есть 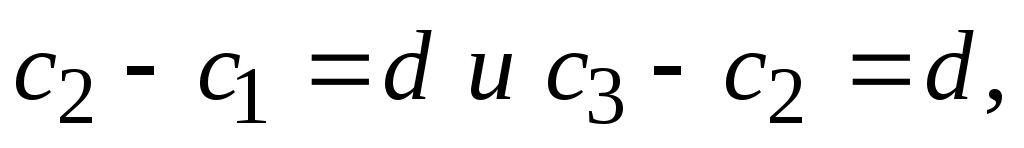 тогда тогда  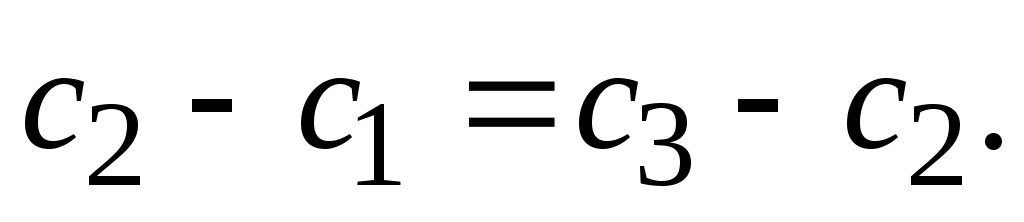
Перейдем к записи условий (б) и (в), используя формулы: 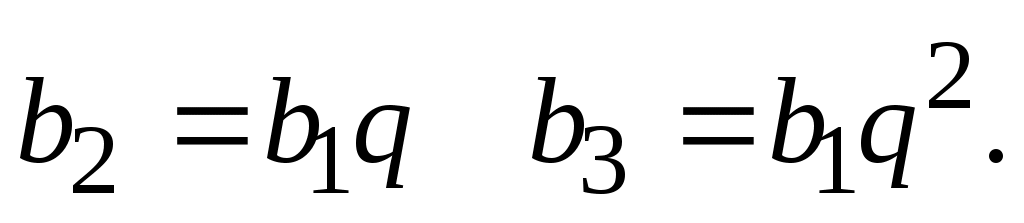 Тогда Тогда
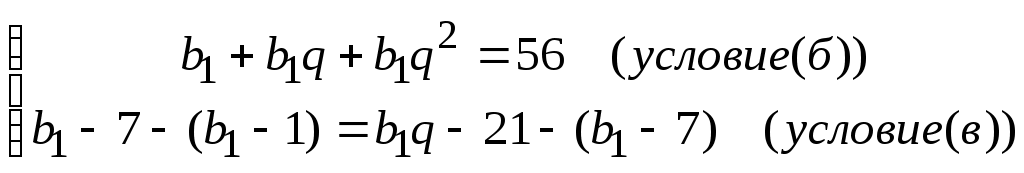
Выполним преобразования и получим

Решим систему методом подстановки 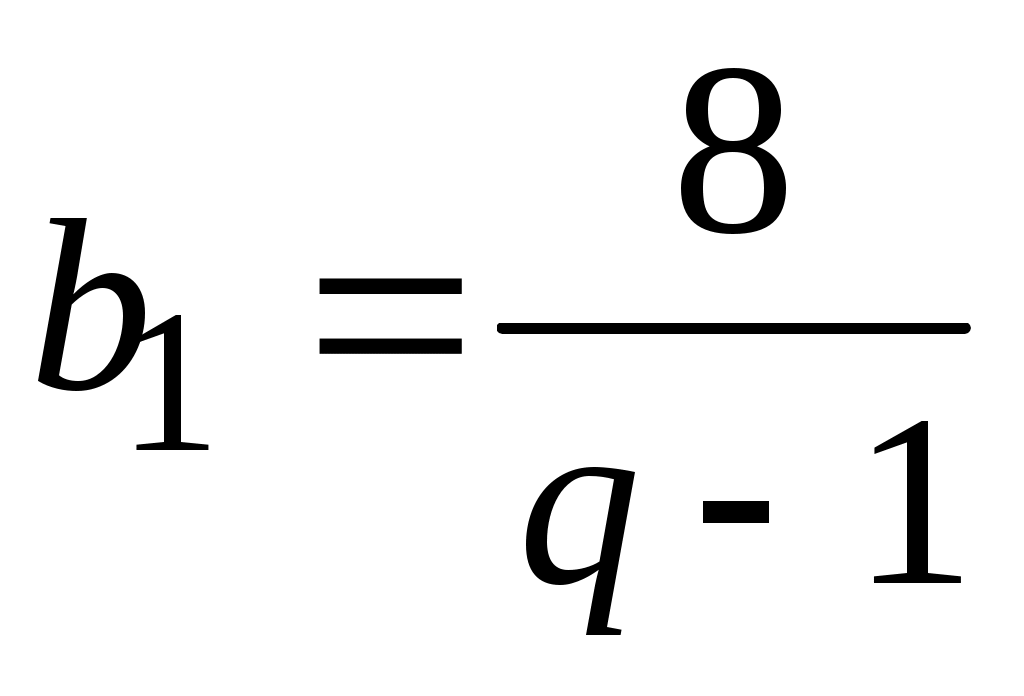 . Первое уравнение системы приобретет вид: . Первое уравнение системы приобретет вид:

Необходимо выбрать значение 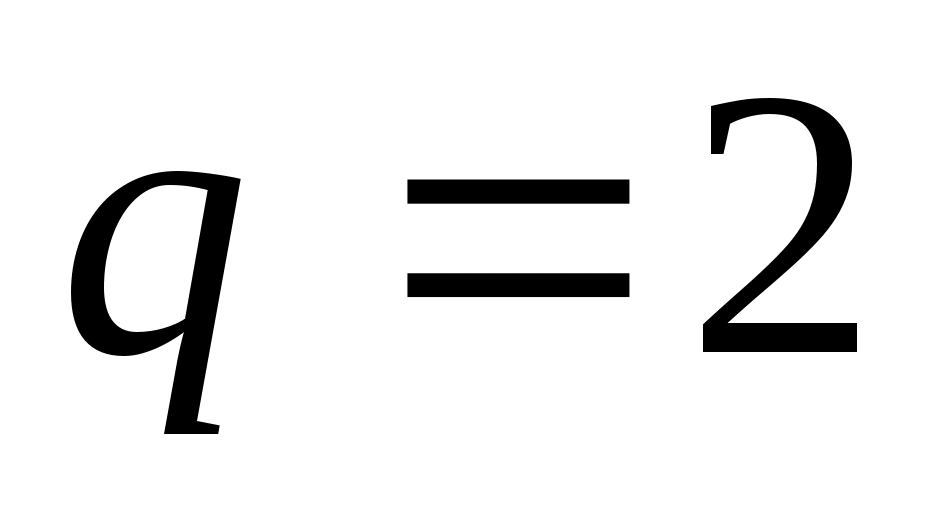 , чтобы выполнилось условие , чтобы выполнилось условие
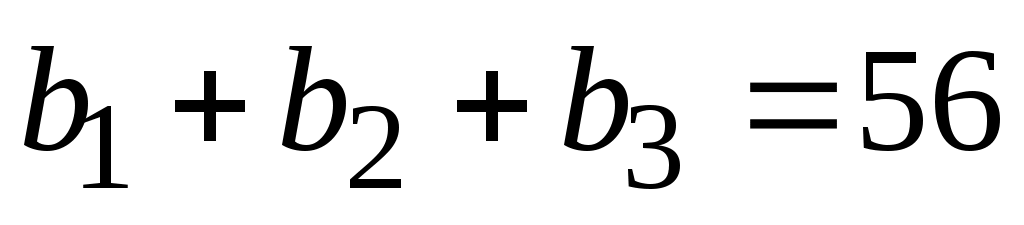 . В этом случае . В этом случае 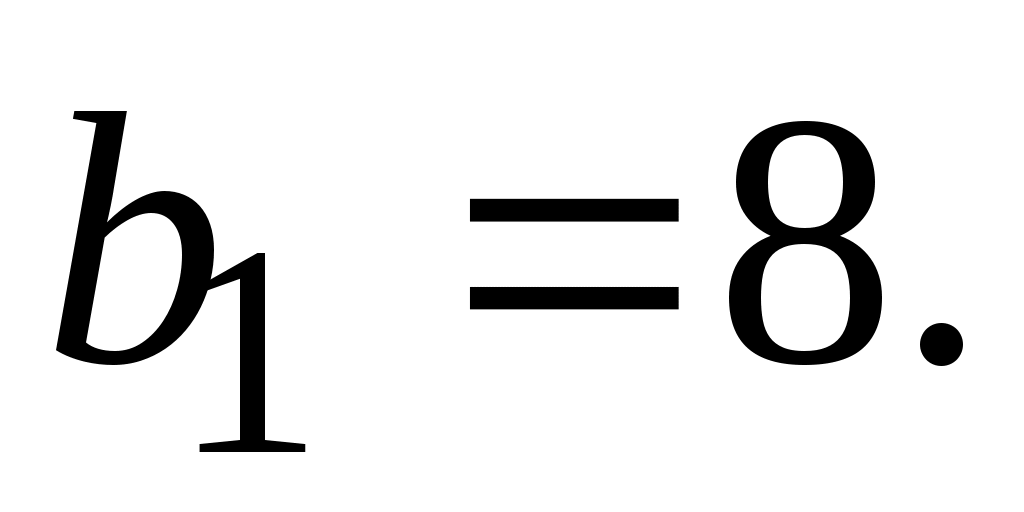 По условию задачи необходимо найти сумму 10 членов геометрической прогрессии, то есть По условию задачи необходимо найти сумму 10 членов геометрической прогрессии, то есть
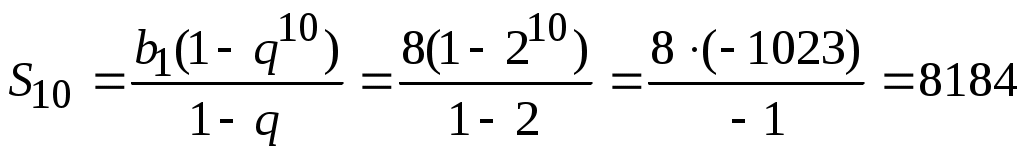 . .
|
|
|
 Скачать 1.98 Mb.
Скачать 1.98 Mb.