Задачи. томский политехнический университет
 Скачать 1.98 Mb.
|
|
§16. Первообразная функции. Определенный интеграл Для решения задач, связанных с первообразной функции (неопределенным интегралом) и определенным интегралом, необходимо знать: 1) таблицу неопределенных интегралов в объеме     2) свойства неопределенного интеграла  , где  - числовой коэффициент.  , где  - первообразная функции  , а  - линейная функция.3)  . Вычисление определенного интеграла представляет собой нахождение числа, равного разности значений первообразной функции в точках верхнего и нижнего пределов определенного интеграла. Это же числовое значение определяет площадь криволинейной трапеции, вид которой можно найти в любом учебнике. Для вычисления площади фигуры, заключенной между графиками функций  необходимо определить значения  как абсциссы точек пересечения графиков : - решить уравнение или определить их из условия задачи. В любой точке  вычислить  . Если, допустим,  , топлощадь фигуры равна  .Пример 51. Найти первообразную функций f(x), проходящую через точку М0 с координатами x0,y0:  а) Найдем первообразную функции:  (аргументом степенной функции является линейная функция 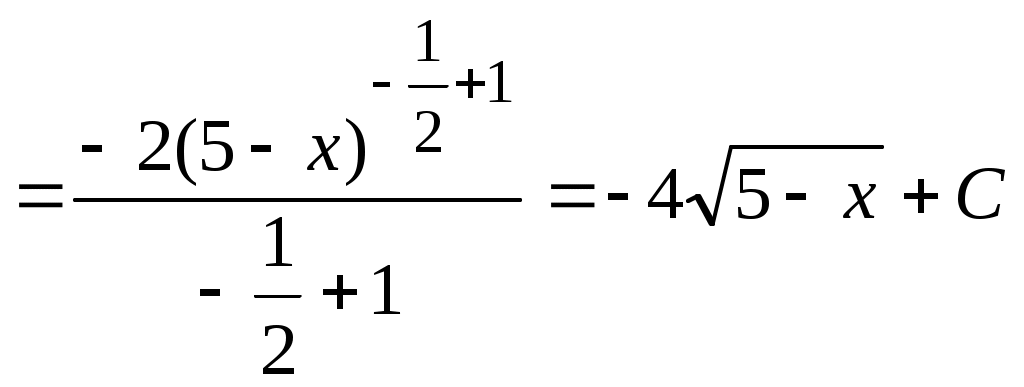 , где =-1) .б) Используя условие задачи  , то есть  ,получим уравнение для определения значения постоянной интегрирования  : -1=-8+ ; Окончательно, .Пример 52. Вычислить площадь фигуры, заключенной между указанными линиями: y=2x; y=x; x=5. а) Функции: y1=2x; y2=x пересекаются в точке с абсциссой x=0 (2x=x), то есть  (нижний предел определенногоинтеграла, который определит искомую площадь фигуры). Значение  определено условием задачи. Тогда . Вычислим  . Значит .Пример 53. Вычислить площадь фигуры, заключенной между линиями: y=x2-x; y=2x. а) Найдем точки пересечения функций y1=x2-x; y2=2x:  .б) Вычислим  . Тогда   §17. Показательные уравнения Способы решения показательных уравнений можно представит, рассматривая два вида уравнений: 1)  , где  -функциональные выражения произвольного вида, а число  0 и  .Тогда равенство показательных выражений левой и правой части уравнений приводит к равенству  , которое представляет собой алгебраическое уравнение, способы решения которого известны. Пример 54.  Преобразуем левую часть уравнения, используя равенства  . Уравнение принимает вид: 2)  , то есть неизвестная величина в уравнении представлена показательной функцией  . Введем новую переменную  (заметим, что  0, так как 0 при любых значениях  ). Далее, будем решать алгебраическое уравнение  и находить значения  (одно или более, зависит от вида уравнения). Затем,  .Пример 55.  Заменим:  , учтем, что . Уравнение будет иметь 3) Наиболее сложными являются показательные уравнения, содержащие две показательные функции с разными основаниями. Для их решения необходимо правильно выбрать алгебраические преобразования, которые приводят уравнение к виду с одной показательной функцией. Рассмотрим решение уравнения такого типа. Пример 56.  Преобразуем  ,  ,  ,  . Уравнение содержит показательные функции: 1) с основанием 2, степени которых  и ; 2) с основанием 5, степени которых  и . Выберем показательные выражения с меньшими степенями, то есть  и  ; разделим левую и правую части уравнения почленно на произведение  . Получим  . Преобразуем и получим результат:  , где  ;  . Заменим  и запишем алгебраическое уравнение  или  . Кубическое уравнение решается подбором корня  . Остаток от деления многочленов  и  равен  . Уравнение  не имеет решения в области вещественных чисел. Поэтому единственный корень определяет  или  ;  .§18. Решение системы показательных уравнений Пример 57. 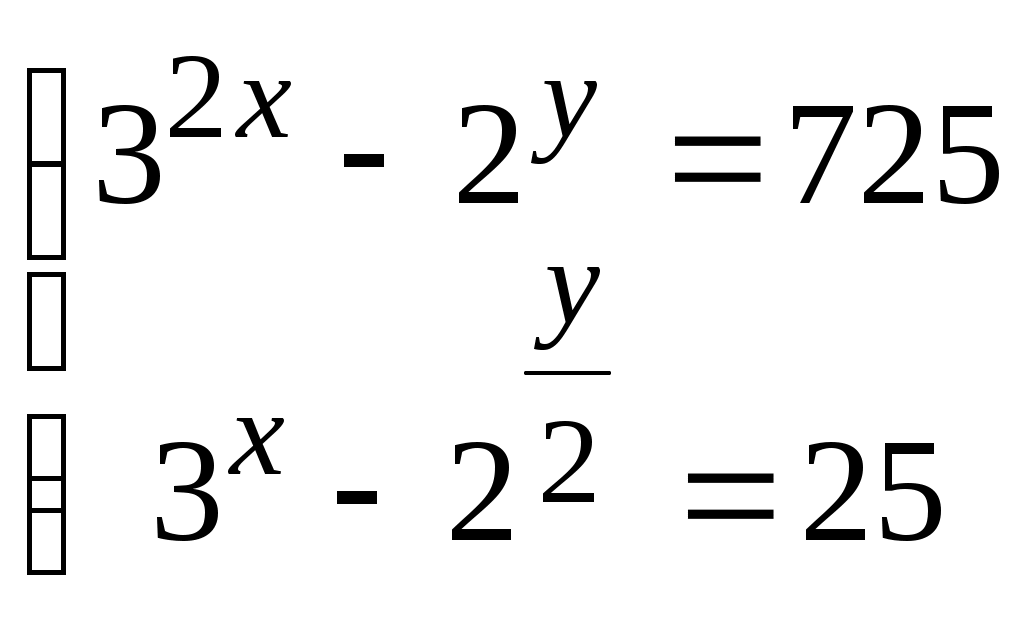 Заменим:  . Тогда система будет иметь вид: Алгебраическую систему уравнений решаем методом подстановки  . Первое уравнение системы представим в виде: Тогда  . Окончательно,  §19. Показательные неравенства При решении показательных неравенств вида  необходимо учитывать значение . При 0< <1 знак неравенств, при сравнении степеней, меняется на противоположный, то есть  При >1 сравнение степеней выполняется с тем же знаком. Полученные алгебраические неравенства решают известными способами в зависимости от вида неравенства. Пример 58.  Учитывая область определения неравенства:  и условие , будем решать неравенство  . Так как  (основание 5>1).Квадратное неравенство имеет решение  С учетом области определения решение задачи:  Пример 59.  0; Рекомендации к решению задачи. Необходимо  представить в виде  , заменить 0 и решать алгебраическое неравенство.Получите решение  и, с учетом того, что 0, решением является интервал (0;4). Тогда 0 4 Пример 60.  Ответ: 1;4.Рекомендации к решению задачи Учесть, что  Использована формула суммы арифметической прогрессии, число членов которой равно .Пример 61.  0; Рекомендации к решению задачи. Представить  Затем, почленно разделить обе части неравенства на произведение  . |