Траектория, путь, перемещение. Скорость движения точки по прямой. Нахождение координаты по известной зависимости скорости от времени
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
31. Первый закон термодинамики. Работа газа при изменении объема. Первое начало термодинамики: Количество теплоты, сообщённое газу, идёт на приращение внутренней энергии газа и на совершение газом работы над внешними телами. 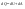 - первое начало термодинамики. Определим физические величины, входящие в этот закон. - первое начало термодинамики. Определим физические величины, входящие в этот закон.а) Внутренняя энергия идеального газа равна 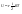 , где , где 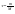 - количество вещества, i – число степеней свободы молекул газа. Тогда изменение внутренней энергии газа равно - количество вещества, i – число степеней свободы молекул газа. Тогда изменение внутренней энергии газа равно  - изменение внутренней энергии газа. - изменение внутренней энергии газа.б) Вычислим теперь работу, совершаемую газом при изменении объёма. Для этого рассмотрим газ, находящийся в цилиндре под поршнем, который может свободно перемещаться.  При нагревании давление газа P , будет оставаться постоянным, и, как видно из рисунка, работа, которую совершает газ, будет равна: При нагревании давление газа P , будет оставаться постоянным, и, как видно из рисунка, работа, которую совершает газ, будет равна:  , где dV=Sdl - изменение объема газа. , где dV=Sdl - изменение объема газа. 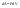 - работа, совершаемая газом при изменении его объема. - работа, совершаемая газом при изменении его объема. в) Наконец, найдём формулу для подсчёта количества теплоты, сообщенной газу массы  при его нагревании на при его нагревании на  . Для этого введем понятие молярной теплоёмкости газа . Для этого введем понятие молярной теплоёмкости газа 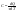 . Молярная теплоёмкость газа – это количество теплоты, сообщённой 1 молю газа, для увеличения его температуры на . Молярная теплоёмкость газа – это количество теплоты, сообщённой 1 молю газа, для увеличения его температуры на  . Тогда формула для подсчёта теплоты будет иметь вид . Тогда формула для подсчёта теплоты будет иметь вид 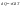 - теплота, сообщённая газу для увеличения его температуры на dT. - теплота, сообщённая газу для увеличения его температуры на dT.32. 0братимые и необратимые процессы. Равновесные и неравновесные процессы. Изопроцессы в газах. Равновесным состоянием системы называется такое состояние, при котором параметры системы имеют определённые значения, остающиеся при неизменных внешних условиях постоянными сколько угодно долго. Процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновесным или квазистатическим. Из сказанного следует, что равновесным может быть только бесконечно медленный процесс. При достаточно медленном протекании реальные процессы могут приближаться к равновесному процессу сколько угодно близко. Равновесный процесс может быть проведен в обратном направлении, причём система будет проходит через те же состояния, что и при прямом ходе, но в обратной последовательности. Поэтому равновесные процессы называют также обратимыми процессами. В случае обратимого процесса при возвращении в исходное состояние ни в самой системе, ни в окружающих телах не остаётся никаких изменений. Если такие изменения появляются, то такой процесс называется необратимым процессом. Все реальные процессы необратимы 1. Термодинамика изохорического процесса: V=const Рассмотрим закон, описывающий этот процесс и его график в координатах (P,V). Этот закон является частным случаем уравнения состояния идеального газа: PV = RT. 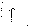 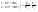 . - закон Шарля. Так как . - закон Шарля. Так как 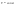 , то , то 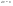 и и 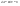 , т.е , т.е  - работа совершаемая газом при изохорическом процессе равна нулю. Тогда - работа совершаемая газом при изохорическом процессе равна нулю. Тогда 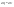 - первое начало термодинамики для изохорического процесса. Поскольку количество теплоты, сообщенное газу, равно - первое начало термодинамики для изохорического процесса. Поскольку количество теплоты, сообщенное газу, равно  , где , где  - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа: - молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа: 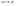 - изменение внутренней энергии газа. Сравнивая эту формулу с другой формулой - изменение внутренней энергии газа. Сравнивая эту формулу с другой формулой 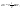 получим выражение для молярной теплоёмкости газа при постоянном объёме: получим выражение для молярной теплоёмкости газа при постоянном объёме: 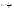 . .
Соотношение Майера Сначала рассмотрим закон, описывающий этот процесс и его график в координатах (P,V). 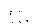 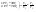 - закон Гей-Люссака. Теперь работа, совершаемая газом, - закон Гей-Люссака. Теперь работа, совершаемая газом, 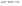 приращение внутренней энергии газа тоже не равно нулю приращение внутренней энергии газа тоже не равно нулю  , и первое начало термодинамики не меняет своего вида: , и первое начало термодинамики не меняет своего вида: 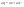 первое начало термодинамики для изобарического процесса. Формула для подсчёта теплоты теперь примет вид первое начало термодинамики для изобарического процесса. Формула для подсчёта теплоты теперь примет вид 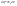 где где  - молярная теплоёмкость газа при постоянном давлении. Приращение внутренней энергии запишем в виде - молярная теплоёмкость газа при постоянном давлении. Приращение внутренней энергии запишем в виде  . Работу, совершаемую газом, также представим в аналогичном виде . Работу, совершаемую газом, также представим в аналогичном виде  . Здесь мы воспользовались уравнением Менделеева-Клапейрона . Здесь мы воспользовались уравнением Менделеева-Клапейрона 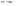 дифференциальное уравнение которого при дифференциальное уравнение которого при 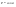 дает дает 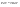 . Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R: . Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R: 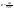 , ,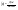 . Универсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус. Продолжим рассмотрение изобарического процесса. Подставляя полученные выражения для dQ, dU, dA в первое начало термодинамики, получим: . Универсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус. Продолжим рассмотрение изобарического процесса. Подставляя полученные выражения для dQ, dU, dA в первое начало термодинамики, получим: 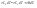 Сокращая на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме Сокращая на dT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме  и постоянном давлении и постоянном давлении  : : 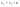 - соотношение Майера. Учитывая выражение для - соотношение Майера. Учитывая выражение для 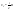 , получим аналогичное выражение для , получим аналогичное выражение для   = =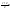 . Приведем также выражение для отношения молярных теплоёмкостей . Приведем также выражение для отношения молярных теплоёмкостей  и и  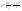 . Для двухатомных молекул при невысоких температурахi= 5, тогда . Для двухатомных молекул при невысоких температурахi= 5, тогда  1,4. Выпишем работу, совершаемую газом при изобарическом процессе (P=const): 1,4. Выпишем работу, совершаемую газом при изобарическом процессе (P=const): 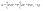 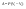 - работа, совершаемая газом при изобарическом процессе. - работа, совершаемая газом при изобарическом процессе.  На графике (P,V) работа, совершаемая газом, численно равна площади прямоугольника, построенного под изобарой. На графике (P,V) работа, совершаемая газом, численно равна площади прямоугольника, построенного под изобарой.3. Термодинамика изотермического процесса: T=const. Приведем закон, описывающий этот процесс, и его график в координатах (P,V). 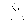 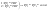 - закон Бойля-Мариотта Так как T = const, то - закон Бойля-Мариотта Так как T = const, то 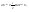 т. е. dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю. Тогда dQ = dA - Первое начало термодинамики при изотермическом процессе. При изотермическом процессе вся теплота, сообщенная газу, идет на работу, совершаемую газом: Q=A. Выпишем работу, совершаемую газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона т. е. dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю. Тогда dQ = dA - Первое начало термодинамики при изотермическом процессе. При изотермическом процессе вся теплота, сообщенная газу, идет на работу, совершаемую газом: Q=A. Выпишем работу, совершаемую газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона 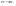 представим элементарную работу в виде: представим элементарную работу в виде: 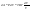 Тогда Тогда 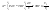 . работа, совершаемая газом при изотермическом процессе . работа, совершаемая газом при изотермическом процессе  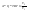 . Учитывая то, что при изотермическом процессе . Учитывая то, что при изотермическом процессе 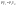 работу можно вычислить также по формуле: работу можно вычислить также по формуле: 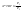 ; ;На графике (P,V) работа, совершаемая газом, численно равна площади под кривой, описывающий изотермический процесс. 33. 34. Адиабатный процесс. Уравнение Пуассона, адиабата. Политропный процесс, уравнение политропы. Термодинамика адиабатического процесса: dQ=0 Несмотря на то, что мы поочерёдно рассмотрели процессы с V=const, P=const, T=const, список характерных газовых процессов этим не исчерпывается. Обратим внимание, что при изохорическом процессе dA=0, при изотермическом процессе dU=0, и поэтому естественно рассмотреть процесс в котором dQ=0, т.е. адиабатический процесс. Адиабатический процесс - это процесс, протекающий без теплообмена с окружающей средой. Поскольку dQ = 0, то первое начало термодинамики примет вид: 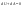 - первое начало термодинамики при адиабатическом процессе. Такой вид первого начала термодинамики позволяет легко вычислить работу, совершаемую газом: - первое начало термодинамики при адиабатическом процессе. Такой вид первого начала термодинамики позволяет легко вычислить работу, совершаемую газом: 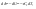 или для конечного адиабатического процесса: или для конечного адиабатического процесса: 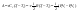 - - работа, совершаемая газом при адиабатическом процессе. Исходя из dU + dA = 0, выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. Для этого dU и dA представим в виде - - работа, совершаемая газом при адиабатическом процессе. Исходя из dU + dA = 0, выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. Для этого dU и dA представим в виде 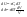 Подставив это выражение в dU + dA = 0, получим дифференциальное уравнение: Подставив это выражение в dU + dA = 0, получим дифференциальное уравнение: 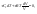 которое, разделив на СVT и используя соотношения которое, разделив на СVT и используя соотношения 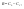 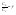 , можно записать в виде , можно записать в виде 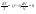 . Это дифференциальное уравнение приводится к полному дифференциалу: . Это дифференциальное уравнение приводится к полному дифференциалу: 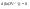 Решение этого дифференциального уравнения имеет вид Решение этого дифференциального уравнения имеет вид 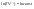 или или 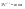 - уравнение адиабатического процесса в переменных(T,V). Воспользовавшись уравнением Менделеева-Клапейрона PV=RT, можно перейти к переменным (P,V) и (T,P). Например, из - уравнение адиабатического процесса в переменных(T,V). Воспользовавшись уравнением Менделеева-Клапейрона PV=RT, можно перейти к переменным (P,V) и (T,P). Например, из 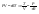 Подставляя это в уравнение Подставляя это в уравнение 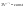 , получим , получим 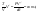 или или 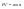 - уравнение Пуассона, - уравнение Пуассона,где  -коэффициент Пуассона. -коэффициент Пуассона. 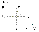 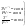 - уравнения адиабаты. - уравнения адиабаты. Политропический процесс Реализованные на практике процессы не всегда можно отнести к какому-либо рассмотренному выше процессу. В этом случае процесс можно считать политропическим. Политропическим процессом называется всякий процесс изменения состояния, при котором теплоёмкость газа С остаётся постоянной и равной 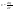 . Отсюда выразим количество теплоты через теплоёмкость газа при политропическом процессе: . Отсюда выразим количество теплоты через теплоёмкость газа при политропическом процессе: 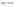 . Используем первое начало термодинамики: . Используем первое начало термодинамики: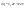 . Здесь . Здесь 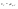 и и 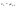 - теплоёмкости газа при постоянном объёме и давлении соответственно. С учётом выражения количества теплоты через теплоёмкость политропического процесса получим - теплоёмкости газа при постоянном объёме и давлении соответственно. С учётом выражения количества теплоты через теплоёмкость политропического процесса получим 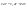 или или 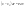 (4.38). Продифференцируем уравнение состояния идеального газа и выразим дифференциал температуры: (4.38). Продифференцируем уравнение состояния идеального газа и выразим дифференциал температуры: 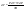 . Учтём, что . Учтём, что 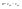 , а , а 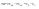 , получим: , получим: 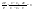 (4.39). Обозначим (4.39). Обозначим 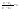 - показатель политропы. После интегрирования (4.39) и дальнейшего потенцирования полученного результата, придём к уравнению политропы: - показатель политропы. После интегрирования (4.39) и дальнейшего потенцирования полученного результата, придём к уравнению политропы: 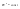 (4.40). Это уравнение может быть выражено и через другие пары параметров состояния, аналогично тому, как это было сделано для адиабатного процесса. (4.40). Это уравнение может быть выражено и через другие пары параметров состояния, аналогично тому, как это было сделано для адиабатного процесса.35. Круговые процессы или циклы. Идеальная тепловая машина и цикл Карно. К.П.Д. идеальной тепловой машины. К.П.Д. реальной тепловой машины. . Процесс, при котором система переходит из состояния 1 в состояние 2, а затем возвращается в состояние 1 через другие промежуточные процессы, называется круговым процессом или циклом. Графически цикл изображается замкнутой кривой. Всякая тепловая машина представляет собой систему, совершающую много кратно некий круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объёма  , а затем сжимается до первоначального объёма , а затем сжимается до первоначального объёма  (рис. 1). Чтобы работа за цикл была больше нуля, давление, (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать теплоту, а в ходе сжатия отнимать от него теплоту. Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемой рабочему телу за цикл, равно (рис. 1). Чтобы работа за цикл была больше нуля, давление, (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать теплоту, а в ходе сжатия отнимать от него теплоту. Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемой рабочему телу за цикл, равно 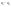 , где , где  – теплота, получаемая рабочим телом при расширении, а – теплота, получаемая рабочим телом при расширении, а  – теплота, отдаваемая при сжатии. Работа – теплота, отдаваемая при сжатии. Работа  , совершаемая за цикл, равна площади цикла. Таким образом, первое начало термодинамики, написанное для цикла, имеет вид , совершаемая за цикл, равна площади цикла. Таким образом, первое начало термодинамики, написанное для цикла, имеет вид 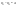 (1). Как следует из этого выражения, не вся получаемая извне теплота (1). Как следует из этого выражения, не вся получаемая извне теплота  используется для получения полезной работы. Коэффициентом полезного действия используется для получения полезной работы. Коэффициентом полезного действия  (сокращённо КПД) тепловой машины называется отношение совершаемой за цикл работы (сокращённо КПД) тепловой машины называется отношение совершаемой за цикл работы  к полученной за цикл теплоте к полученной за цикл теплоте  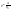 . Приняв во внимание соотношение (1), выражение для КПД можно записать в виде . Приняв во внимание соотношение (1), выражение для КПД можно записать в виде 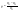 . .Второе начало термодинамики: Невозможно построить периодически действующую тепловую машину, которая бы всю подводимую к ней теплоту превращала в работу, т.е. всегда 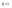 . .Цикл Карно и его КПД Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е. 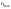 . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. 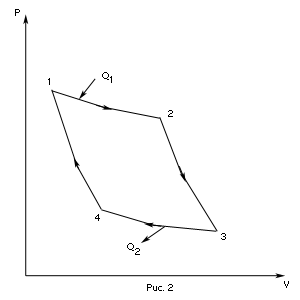  - изотермическое расширение при - изотермическое расширение при  , , - адиабатическое расширение, - адиабатическое расширение,  , , - изотермическое сжатие при - изотермическое сжатие при  , , - изотермическое сжатие, - изотермическое сжатие, 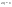 . .Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты  равно работе равно работе  , совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна , совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна 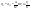 где где  – масса идеального газа в тепловой машине. Количество отдаваемой холодильнику теплоты – масса идеального газа в тепловой машине. Количество отдаваемой холодильнику теплоты  равно работе равно работе  , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна 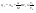 . Для того чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие . Для того чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие 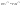 . Аналогично для состояний 2 и 3 должно вытекать условие . Аналогично для состояний 2 и 3 должно вытекать условие 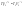 . Разделив одно соотношение на другое, приходим к условию замкнутости цикла . Разделив одно соотношение на другое, приходим к условию замкнутости цикла 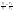 . Теперь подставляя . Теперь подставляя  и и  в выражение для КПД, получим в выражение для КПД, получим 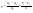 (2). В результате получим формулу для КПД цикла Карно: (2). В результате получим формулу для КПД цикла Карно: 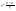 , где , где  - температура нагревателя, - температура нагревателя,  - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах  и и  . Вернёмся к соотношению (2), которое имеет место в случае обратимого цикла Карно. В общем случае при возможности необратимого цикла Карно это соотношение примет вид: . Вернёмся к соотношению (2), которое имеет место в случае обратимого цикла Карно. В общем случае при возможности необратимого цикла Карно это соотношение примет вид: 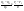 (3). Преобразуем (3) следующим образом: (3). Преобразуем (3) следующим образом: 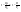 , , 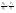 , или , или 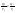 В результате получим В результате получим 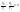 . Для обратимого цикла Карно: . Для обратимого цикла Карно: 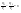 , для необратимого цикла Карно: , для необратимого цикла Карно: 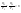 . Для произвольного обратимого цикла: . Для произвольного обратимого цикла: 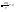 , для произвольного необратимого цикла: , для произвольного необратимого цикла:  . . |
