Траектория, путь, перемещение. Скорость движения точки по прямой. Нахождение координаты по известной зависимости скорости от времени
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
Момент инерции твердого телаРассмотрим твёрдое тело, которое может вращаться вокруг неподвижной вертикальной оси. Чтобы удержать ось от перемещений в пространстве, заключим её в подшипники. Опирающийся па нижний подшипник фланец Фл , предотвращает передвижение оси в вертикальном направлении .  Абсолютно твёрдое тело можно рассматривать как систему материальных точек с неизменным расстоянием между ними. Линейная скорость элементарной массы Абсолютно твёрдое тело можно рассматривать как систему материальных точек с неизменным расстоянием между ними. Линейная скорость элементарной массы  равна равна  , где , где  -расстояние массы -расстояние массы  от оси вращения. Следовательно, для кинетической энергии элементарной массы получается выражение от оси вращения. Следовательно, для кинетической энергии элементарной массы получается выражение 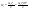 . Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей. . Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей. 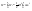 . Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения . Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения 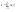 - момент инерции твёрдого тела..Слагаемые этой суммы представляют момент инерции материальной точки относительно оси вращения - момент инерции твёрдого тела..Слагаемые этой суммы представляют момент инерции материальной точки относительно оси вращения  - момент инерции материальной точки относительно оси вращения. Размерность момента инерции [ I ]= 1 кг - момент инерции материальной точки относительно оси вращения. Размерность момента инерции [ I ]= 1 кг . Таким образом, кинетическая энергия тела вращающегося вокруг неподвижной оси, равна . Таким образом, кинетическая энергия тела вращающегося вокруг неподвижной оси, равна 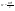 - кинетическая энергия вращающегося твёрдого тела. - кинетическая энергия вращающегося твёрдого тела. 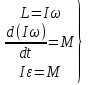 – уравнение вращательного движения тела. Произведение момента инерции тела на угловое ускорение равно моменту внешних сил относительно неподвижной оси вращения. – уравнение вращательного движения тела. Произведение момента инерции тела на угловое ускорение равно моменту внешних сил относительно неподвижной оси вращения.16. Работа при вращении тела. Условия равновесия твердого тела. 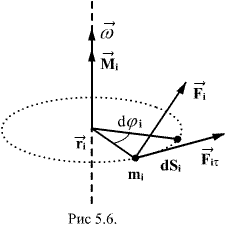 Рассмотрим действие внешней силы  , приложенной к точке массой , приложенной к точке массой  . За время . За время 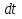 элементарная масса элементарная масса 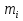 проходит путь проходит путь 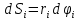 . Работа силы . Работа силы 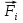 на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей 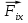 силы. силы. 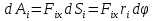 . Но . Но 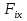 равна модулю момента равна модулю момента 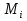 силы силы 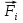 относительно оси вращения. Работа относительно оси вращения. Работа 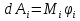 , и будет положительна, если , и будет положительна, если 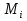 имеет такое же направление, как и имеет такое же направление, как и 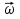 отрицательное, если направление векторов отрицательное, если направление векторов 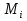 и и 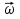 противоположны. противоположны.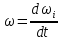 . С учетом, что . С учетом, что 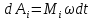 . Работа всех сил, приложенных к телу . Работа всех сил, приложенных к телу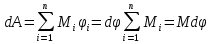 . Полная работа . Полная работа 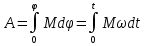 17. Теорема Гюйгенса - Штейнера. Момент инерции и кинетическая энергия вращения твердого тела вокруг неподвижной оси. Момент инерции тела относительно нецентральной оси. Теорема Штейнера. Пусть тело вращается вокруг неподвижной нецентральной оси. Это тело обладает кинетической энергией 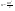 (1), (1),  где I - момент инерции тела относительно данной нецентральной оси где I - момент инерции тела относительно данной нецентральной оси . Проведём через центр масс С ось ОО , параллельную данной нецентральной оси . Проведём через центр масс С ось ОО , параллельную данной нецентральной оси 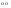 . Тогда вращение твёрдого тела можно представить как результат вращения центра масс С вокруг оси . Тогда вращение твёрдого тела можно представить как результат вращения центра масс С вокруг оси 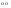 и вращение твёрдого тела вокруг центральной оси ОО тоже с угловой скоростью . Кинетическую энергию тоже можно представить как сумму двух слагаемых. и вращение твёрдого тела вокруг центральной оси ОО тоже с угловой скоростью . Кинетическую энергию тоже можно представить как сумму двух слагаемых. 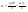 (2); где (2); где 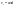 - линейная скорость центра масс. C учётом (1) и (2) получаем - линейная скорость центра масс. C учётом (1) и (2) получаем 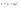 - теорема Штейнера. Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями : - теорема Штейнера. Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями : 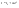 Таким образом, теорема Штейнера, по существу, сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела. Таким образом, теорема Штейнера, по существу, сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела. Линейная скорость элементарной массы  равна равна  , где , где  -расстояние массы -расстояние массы  от оси вращения. Следовательно, для кинетической энергии элементарной массы получается выражение от оси вращения. Следовательно, для кинетической энергии элементарной массы получается выражение 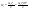 . Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей. . Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей. 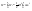 . Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения . Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения 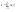 - момент инерции твёрдого тела. Таким образом, кинетическая энергия тела вращающегося вокруг неподвижной оси, равна - момент инерции твёрдого тела. Таким образом, кинетическая энергия тела вращающегося вокруг неподвижной оси, равна 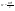 - кинетическая энергия вращающегося твёрдого тела. - кинетическая энергия вращающегося твёрдого тела.18. Инвариантность законов динамики в ИСО. Сила инерции. Пусть одна система движется относительно другой равномерно и прямолинейно со скоростью 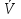 тогда тогда 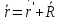 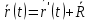 . Необходимо заметить что инерциальность с/с отсчета здесь фактически не использована поэтому закон сложения скоростей справедлив и в случае если 2-ая система движется ускоренно но не вращается . Необходимо заметить что инерциальность с/с отсчета здесь фактически не использована поэтому закон сложения скоростей справедлив и в случае если 2-ая система движется ускоренно но не вращается 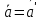 абсолютное уск-ие равно относительному, это означает что ускорение инвариантно при переходе из одной ИСО в другое. абсолютное уск-ие равно относительному, это означает что ускорение инвариантно при переходе из одной ИСО в другое. 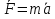 , , 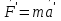 . Сила зависит от разности . Сила зависит от разности 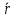 и разности скоростей поэтому и сила инвариантно при переходе из одной ИСО в др. и разности скоростей поэтому и сила инвариантно при переходе из одной ИСО в др. Система отсчета движется поступательно и ускоренно. Выберем 2-ую с/с так чтобы она двигалась относительно первой ИСО прямо и ускоренно. 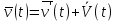 , , 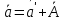 , где , где 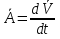 я-ся переносным ускорением и тогда я-ся переносным ускорением и тогда 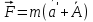 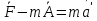 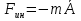 Для того чтобы сохранить формулировку закона ньютона в НИСО надо добавить силу инерции возникающего за счет Для того чтобы сохранить формулировку закона ньютона в НИСО надо добавить силу инерции возникающего за счет19. Система отсчета равномерно вращается (материальная точка покоится в НИСО, материальная точка движется в НИСО). Теорема Кориолиса. Пусть дан диск который равномерно вращается с угловой скоростью ω и пусть шарик соединен с центром диска пружиной. Шарик покоится. В этом случае он занимает положение при к-ом сила натяжения пружины оказывается равной 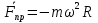 так выглядит ситуация со стороны ИСО. Свяжем с диском и вращающуюся с/с отсчета в к-ой диск и шарик покоятся т.е нах-ся в равновесии. Тут равновесие можно объяснить действием силы инерции так выглядит ситуация со стороны ИСО. Свяжем с диском и вращающуюся с/с отсчета в к-ой диск и шарик покоятся т.е нах-ся в равновесии. Тут равновесие можно объяснить действием силы инерции 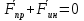 . . 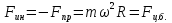 Силу инерции действующую на м/т в равномерно вращающейся с/с отсчета называют центробежной силой. Д.т.ч. описать состояние покоя в такой НИСО необходимо учитывать центробежную силу инерции. Силу инерции действующую на м/т в равномерно вращающейся с/с отсчета называют центробежной силой. Д.т.ч. описать состояние покоя в такой НИСО необходимо учитывать центробежную силу инерции.Пусть шарик масоой m движется вдоль радиуса 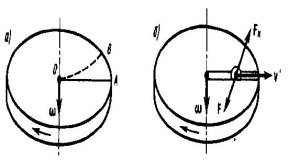 с постоянной скоростью с постоянной скоростью 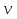 . Начнем вращать диск с . Начнем вращать диск с 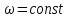 тогда когда шарик достигнет края окажется в точке В. тогда когда шарик достигнет края окажется в точке В. 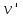 относительно диска. Поэтому в с/с связанной с вращающимся диском на шарик действовала сила инерции кот-ую назвали силой Кориолиса. относительно диска. Поэтому в с/с связанной с вращающимся диском на шарик действовала сила инерции кот-ую назвали силой Кориолиса. 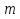 движется относительно вращающейся с/сы отсчета равномерно по ркружности в перпенд плоскости оси вращеня движется относительно вращающейся с/сы отсчета равномерно по ркружности в перпенд плоскости оси вращеня 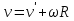 . Для того чтобы частица двигалась по окружности относительно ИСО на неё д.действовать сила направленная к центру окружности . Для того чтобы частица двигалась по окружности относительно ИСО на неё д.действовать сила направленная к центру окружности 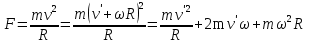 . В НИСО . В НИСО 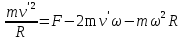 , , 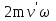 - сила Кориолиса. - сила Кориолиса. 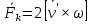 сила кориолиса действует только на тела движущиеся относительно вращающейся системы отсчета и сила кориолиса действует только на тела движущиеся относительно вращающейся системы отсчета и 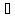 -на -на 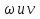 , находится по правилу буравчика. , находится по правилу буравчика.20. Законы Кеплера и обобщение Ньютона (закон всемирного тяготения). Сила тяжести. Поле тяготения. Космические скорости. 1) Все планеты движутся по эллиптическим орбитам, причем Солнце находится в одном из фокусов орбиты. 2) Отрезок, соединяющий Солнце с планетой, описывает равные площади за равные промежутки времени. 3) Квадраты периодов обращения нескольких планет вокруг Солнца относятся, как кубы больших полуосей эллипсов.  1) Мы показали, что замкнутые орбиты являются эллипсами. 2) Второй закон Кеплера представляет собой закон сохранения момента импульса. 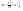 - вектор площади треугольника. - вектор площади треугольника. - секторальная площадь. - секторальная площадь. 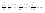  3) Для эллипсов вывод более громоздкий, но для круговых орбит просто: 3) Для эллипсов вывод более громоздкий, но для круговых орбит просто: 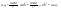  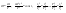 Кеплеровские законы были уточнены и объяснены на основе закона всемирного тяготения Исааком Ньютоном. Закон же всемирного тяготения гласит: Сила F взаимного притяжения между материальными точками массами m1 и m2, находящиеся на расстоянии r друг от друга, равна: F=Gm1m2/r^2, где G - гравитационная постоянная. Закон открыт Ньютоном также в XVII веке (понятно, что на основе законов Кеплера). Таким образом в формулировке Ньютона законы Кеплера звучат так: - первый закон: под дествием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. Надо сказать, что он справедлив для всех тел, между которыми действует взаимное притяжение. - формулирование второго закона Кеплера не дана, так как в этом не было необходимости. - третий закон Кеплера сформулирован Ньютоном так: квадраты сидерических периодов планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших полуосей орбит планет. СИЛА ТЯЖЕСТИ Частным, но крайне важным для нас видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Согласно закону всемирного тяготения, она выражается формулой 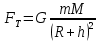 где 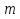 – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли. – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.ГРАВИТАЦИОННОЕ ПОЛЕ, пространство вокруг предмета, чья масса способна притягивать другой предмет. Сила этого притяжения, разделенная на массу второго предмета, и есть сила гравитационного поля. Предмет с большой массой, такой как Земля, имеет мощное гравитационное поле, и оказываемое им воздействие называется силой гравитации (или тяготения). Слабая гравитационная сила существует даже между очень маленькими частицами. Элементарная работа перемещения тела массой m в поле тяготения небесного тела массой М равна откуда находим взлетную скорость, позволяющую вывести корабль на круговую орбиту радиусом r: Для Земли υ2z = 11,2 км/с. Все эти рассуждения справедливы для изолированной планеты. Однако, если планета входит в планетную систему, имеющую центральное светило — Солнце, то, освободившись от тяготения планеты, корабль отнюдь не избавится от притяжения Солнца. Теперь он станет обращаться по замкнутой траектории вокруг Солнца. Чтобы разорвать путы солнечного притяжения, мы должны сообщить кораблю параболическую скорость относительно Солнца: Для Земли υorb = 29,8 км/с и υpar C = 42,1 км/с. Означает ли это, что мы обязаны разогнать корабль до скорости 42,1 км/с для того, чтобы он ушел произвольно далеко от Солнца? Конечно, нет, ведь мы можем использовать грандиозную катапульту, которой снабдила нас природа,— Землю, несущуюся по своей орбите со скоростью υorb. Легко понять, что для Земли скорость, позволяющая, хотя бы в принципе, долететь до любого космического объекта, расположенного в плоскости орбиты Земли за пределами Солнечной системы,— третья космическая скорость — равна Итак, сообщив кораблю скорость υ3 у поверхности Земли, мы можем послать его к любой звезде, лежащей в плоскости обращения Земли. К любой, кроме ближайшей — Солнца! |
