Траектория, путь, перемещение. Скорость движения точки по прямой. Нахождение координаты по известной зависимости скорости от времени
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
21. Элементы специальной (частной) теории относительности. Постулаты Эйнштейна. Преобразования Лоренца и их следствия. Основной закон релятивисткой динамики материальной точки. Закон взаимосвязи массы и энергии. В основе специальной теории относительности лежат постулаты Эйнштейна, сформулированные им в 1905 г. I. Принцип относительности: никакие опыты (механические, электрические, оптические), проведенные внутри даннойинерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. II. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источник света или наблюдателя и одинакова во всех инерциальных системах отсчета. 22. Гармонический осциллятор. Превращения энергии при колебаниях осциллятора. Примеры гармонических осцилляторов (физический маятник, математический маятник). Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы , пропорциональной смещению. Потен mv2/2, потенциальная kx2/2. 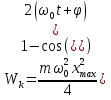 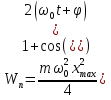 Кин. И потен. Энергии меняются в противофазе вокруг общего среднего значения с удвоенной частотой с течением времени кинетическая переходит в потенциальную и наоборот. Полная энергия остается постоянной. 23. Плотность среды и давление в гидростатике. Основные законы гидростатики. Барометрическая формула. Жидкости и газы находятся в напряженном сжатом состоянии. Степень напряженности хар-ся давлением 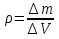 . Выделим мысленно мелкую площадку внутри объема жидкости. На площадку с 2-х сторон действуют силы происходящие от беспорядоченного движения молекул. Пусть сила с одной стороны, с другой тоже равнa ΔF, тогда давление на площадку называют отношение сила нормально действующей на площадку к величине площадки ΔS: . Выделим мысленно мелкую площадку внутри объема жидкости. На площадку с 2-х сторон действуют силы происходящие от беспорядоченного движения молекул. Пусть сила с одной стороны, с другой тоже равнa ΔF, тогда давление на площадку называют отношение сила нормально действующей на площадку к величине площадки ΔS: 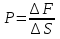 Закон паскаля давление в любом месте покоящейся жидкости одинакова по всем направлениям и одинаково передаются по всему объему занимаемому жидкостью (этот закон справедлив в достаточно малом объеме когда сила тяжести действующая на данный объем во много раз меньше сил давления на его стенки. АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. 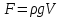  Известно, что атмосферное давление с высотой уменьшается. Установим закон изменения атмосферного давления в зависимости от высоты. Упростим задачу, считая температуру постоянной и не изменяющейся с высотой. При возрастании высоты на небольшую величину dxдавление уменьшается на малую величину Известно, что атмосферное давление с высотой уменьшается. Установим закон изменения атмосферного давления в зависимости от высоты. Упростим задачу, считая температуру постоянной и не изменяющейся с высотой. При возрастании высоты на небольшую величину dxдавление уменьшается на малую величину  , где - плотность газа, = m0n, m0 - масса молекулы. Удобно выразить плотность газа через макропараметры – температуру и давление. Для этого воспользуемся формулой (2.5) и получим , где - плотность газа, = m0n, m0 - масса молекулы. Удобно выразить плотность газа через макропараметры – температуру и давление. Для этого воспользуемся формулой (2.5) и получим  , тогда , тогда  , а , а 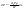 . Разделим переменные . Разделим переменные 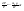 Интегрируя, получаем: Интегрируя, получаем: 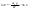 , где С - постоянная интегрирования, которую находим из условия : при x=0 и С=Р0 . Тогда , где С - постоянная интегрирования, которую находим из условия : при x=0 и С=Р0 . Тогда 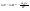 или или 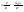 . После потенцирования получим барометрическую формулу . После потенцирования получим барометрическую формулу 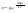 (3.15). Учитывая, что масса молекулы может быть выражена через молярную массу и число Авогадро (3.15). Учитывая, что масса молекулы может быть выражена через молярную массу и число Авогадро 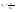 , а , а 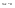 , показатель экспоненты можно записать через молярную массу и универсальную газовую постоянную: , показатель экспоненты можно записать через молярную массу и универсальную газовую постоянную: 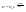 (3.15'). (3.15').24. Понятие потока жидкости (газа) и уравнение непрерывности. Вывод уравнения Бернулли. Теорема Торричелли. Течение в горизонтальной трубе. Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости  , как функцию времени , как функцию времени 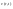 . Стационарное течение – это установившееся движение жидкости, при котором вектор скорости в каждой точке пространства остаётся постоянным, т.е. . Стационарное течение – это установившееся движение жидкости, при котором вектор скорости в каждой точке пространства остаётся постоянным, т.е. 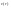 . Линии тока - это линии, проведённые в движущейся жидкости так, что касательные к ним в каждой точке совпадают по направлению с вектором скорости . Линии тока - это линии, проведённые в движущейся жидкости так, что касательные к ним в каждой точке совпадают по направлению с вектором скорости . Густота линий тока пропорциональна величине скорости в данном месте. Трубка тока – это часть жидкости, ограниченная линиями тока.Частицы жидкости при своём движении не пересекают стенок трубки тока. . Густота линий тока пропорциональна величине скорости в данном месте. Трубка тока – это часть жидкости, ограниченная линиями тока.Частицы жидкости при своём движении не пересекают стенок трубки тока. 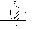 Возьмем несжимаемую жидкость и рассмотрим в ней трубку тока. Объём жидкости, прошедшей через поперечное сечение S за время t, равен Svt. Тогда Q = Sv - поток жидкости, т.е. объём жидкости, прошедшей через поперечное сечение S за единицу времени. Возьмем несжимаемую жидкость и рассмотрим в ней трубку тока. Объём жидкости, прошедшей через поперечное сечение S за время t, равен Svt. Тогда Q = Sv - поток жидкости, т.е. объём жидкости, прошедшей через поперечное сечение S за единицу времени. 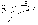 Если жидкость несжимаема, то объем жидкости между сечениями S1 и S2 будет оставаться неизменным, и тогда S1v1= S2v2 . Это справедливо для любой пары S1 и S2 , и мы получаем Sv = const – теорема о неразрывности струи: Для несжимаемой жидкости величина потока жидкости Sv в любом сечении одной и той же трубки тока должна быть одинаковой. Если жидкость несжимаема, то объем жидкости между сечениями S1 и S2 будет оставаться неизменным, и тогда S1v1= S2v2 . Это справедливо для любой пары S1 и S2 , и мы получаем Sv = const – теорема о неразрывности струи: Для несжимаемой жидкости величина потока жидкости Sv в любом сечении одной и той же трубки тока должна быть одинаковой.Стационарное движение идеальной жидкости. Уравнение Бернулли. Идеальная жидкость – жидкость, в которой внутреннее трение (вязкость) полностью отсутствует. 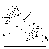 Рассмотрим стационарное течение идеальной жидкости. Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. Рассмотрим объём жидкости V, ограниченный стенками трубки токаи и перпендикулярными к линиям тока сечениями S1 и S2. За время t этот объём переместится. В силу непрерывности струи: V1= V2=V. Энергия каждой частицы жидкости складывается из её кинетической и потенциальной энергии. Вследствие стационарности течения приращение энергии Е всего рассматриваемого объёма V можно вычислить как разность энергий заштрихованных объёмов V1 и V2. Рассмотрим стационарное течение идеальной жидкости. Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. Рассмотрим объём жидкости V, ограниченный стенками трубки токаи и перпендикулярными к линиям тока сечениями S1 и S2. За время t этот объём переместится. В силу непрерывности струи: V1= V2=V. Энергия каждой частицы жидкости складывается из её кинетической и потенциальной энергии. Вследствие стационарности течения приращение энергии Е всего рассматриваемого объёма V можно вычислить как разность энергий заштрихованных объёмов V1 и V2. 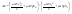 где плотность жидкости. В идеальной жидкости приращение энергии должно равняться работе, совершаемой над выделенным объёмом силами давления: Е = А (1), А = P1S1l1 - P2S2l2 = (P1 - P2)V. Подставляя в (1) и сократив V, получим: где плотность жидкости. В идеальной жидкости приращение энергии должно равняться работе, совершаемой над выделенным объёмом силами давления: Е = А (1), А = P1S1l1 - P2S2l2 = (P1 - P2)V. Подставляя в (1) и сократив V, получим: 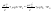 . Поскольку сечения S1 и S2 произвольные, то это справедливо в любом сечении трубки тока. В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие: . Поскольку сечения S1 и S2 произвольные, то это справедливо в любом сечении трубки тока. В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие: 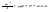 – уравнение Бернулли. Для горизонтальной линии тока уравнение Бернулли примет вид: – уравнение Бернулли. Для горизонтальной линии тока уравнение Бернулли примет вид: 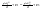 , т.е. давление оказывается меньшим в тех точках, где скорость больше. , т.е. давление оказывается меньшим в тех точках, где скорость больше.Истечение жидкости из отверстия Рассмотрим  истечение жидкости из небольшого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность, а с другой стороны – отверстие, через которое вытекает жидкость. P1 = P2 – давления в обоих сечениях равны атмосферному. Скорость перемещения открытой поверхности в широком сосуде положим, равна нулю. Тогда: истечение жидкости из небольшого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность, а с другой стороны – отверстие, через которое вытекает жидкость. P1 = P2 – давления в обоих сечениях равны атмосферному. Скорость перемещения открытой поверхности в широком сосуде положим, равна нулю. Тогда: 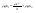 , где v – скорость течения из отверстия. Отсюда: , где v – скорость течения из отверстия. Отсюда: 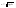 - формула Торричелли, где h = h1 - h2. -импульс силы. - формула Торричелли, где h = h1 - h2. -импульс силы. 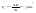 - реакция вытекающей струи. - реакция вытекающей струи. 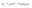 Течение жидкости по трубе. Формула Пуазейля.  Пологая течение жидкости ламинарным, найдём закон изменения скорости vс расстоянием r от оси трубы, т.е. v(r) -? Выделим воображаемый цилиндрический объём жидкости радиуса rи длинны l. Поскольку скорости всех частиц жидкости являются постоянными v = const, сумма внешних сил, приложенных к любому объёму жидкости, равна нулю. На основание цилиндра действуют силы давления, сумма которых равна: Пологая течение жидкости ламинарным, найдём закон изменения скорости vс расстоянием r от оси трубы, т.е. v(r) -? Выделим воображаемый цилиндрический объём жидкости радиуса rи длинны l. Поскольку скорости всех частиц жидкости являются постоянными v = const, сумма внешних сил, приложенных к любому объёму жидкости, равна нулю. На основание цилиндра действуют силы давления, сумма которых равна: 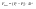 . На боковую поверхность цилиндра действует сила трения: . Поскольку , то . Учитывая, что скорость убывает с расстоянием от оси трубы, т.е. , из (1) получим: , . Интегрирование даёт: . Так как при r = R скорость v= 0, то , где R - радиус трубы. . На боковую поверхность цилиндра действует сила трения: . Поскольку , то . Учитывая, что скорость убывает с расстоянием от оси трубы, т.е. , из (1) получим: , . Интегрирование даёт: . Так как при r = R скорость v= 0, то , где R - радиус трубы.  - закон изменения скорости жидкости от расстояния до оси трубы. Если - скорость на оси трубы, то - закон изменения скорости жидкости от расстояния до оси трубы. Если - скорость на оси трубы, то  Вычислим поток жидкости Q – т. е. объём жидкости, протекающей через поперечное сечение трубы за единицу времени. Для этого сначала определим поток жидкости через кольцо радиуса r и толщиной dr : Вычислим поток жидкости Q – т. е. объём жидкости, протекающей через поперечное сечение трубы за единицу времени. Для этого сначала определим поток жидкости через кольцо радиуса r и толщиной dr : 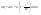 -поток жидкости через кольцо dr. Интегрируя по r, получим поток жидкости через поперечное сечение трубы: -поток жидкости через кольцо dr. Интегрируя по r, получим поток жидкости через поперечное сечение трубы: 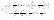  -формула Пуазеля . Ее можно использовать для определения коэффициента вязкости -формула Пуазеля . Ее можно использовать для определения коэффициента вязкости . .25. Вязкость. Ламинарное течение в трубе. Формула Пуазейля. Турбулентное течение жидкости. Число Рейнольдса. Гидродинамика вязкой жидкости. Коэффициент вязкости. Ламинарные и турбулентные течения. Всем реальным жидкостям и газам присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается. Рассмотрим следующий опыт:  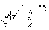 В жидкость погружены две параллельные друг другу пластины, линейные размеры которых значительно превосходят расстояние между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней с некоторой скоростью В жидкость погружены две параллельные друг другу пластины, линейные размеры которых значительно превосходят расстояние между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней с некоторой скоростью  под действием постоянной силы под действием постоянной силы  . Пусть S - площадь поверхности пластин, тогда -- сила трения, действующая на пластину при ее движении, где - коэффициент внутреннего трения или коэффициент вязкости. Опыт показывает, что - скорость частиц жидкости в разных слоях. Так как - модуль градиента скорости. - сила внутреннего трения между слоями жидкости при ее движении. Размерность коэффициент вязкости: в СИ , в СГС . 1 Па с=10 П. У жидкостей коэффициент вязкостиуменьшается с увеличением температуры, у газов наоборот. Наблюдается два вида течения жидкости (газа): . Пусть S - площадь поверхности пластин, тогда -- сила трения, действующая на пластину при ее движении, где - коэффициент внутреннего трения или коэффициент вязкости. Опыт показывает, что - скорость частиц жидкости в разных слоях. Так как - модуль градиента скорости. - сила внутреннего трения между слоями жидкости при ее движении. Размерность коэффициент вязкости: в СИ , в СГС . 1 Па с=10 П. У жидкостей коэффициент вязкостиуменьшается с увеличением температуры, у газов наоборот. Наблюдается два вида течения жидкости (газа):
Английский учёный Рейнольдс установил, что характер течения жидкости зависит от значения безразмерной величины: - число Рейнольдса, где l характерный для поперечного сечения размер. Как видно из этого выражения, имеет смысл ввести новую характеристику вязкой жидкости: - кинематический коэффициент вязкости. 26. Параметры, определяющие состояние вещества. Идеальный газ. Вывод основного уравнения кинетической теории газов. Вывод основных газовых законов. Уравнение состояния идеальных газов. Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. Состояние заданной массы m идеального газа определяется значениями трёх параметров: давления P, объёма V, и температуры Т. Уравнение состояния идеального газа или уравнение Менделеева - Клапейрона является обобщением законов идеального газа, открытых экспериментально до создания МКТ. Однако, из основного уравнения МКТ (2.3), можно получить уравнение состояния идеального газа. Для этого подставим вместо средней кинетической энергии поступательного движения молекулы в основное уравнение МКТ идеальных газов правую часть равенства (2.4), получим уравнение, в которое не входят микропараметры газа  (2.5). Так как (2.5). Так как 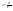 , следовательно, , следовательно, 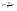 или или . Учитывая, что . Учитывая, что 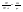 , получим N=NA , получим N=NA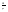 , а так как NAk = R = 8,3 , а так как NAk = R = 8,3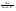 - молярная газовая постоянная [2,3,5,15] или универсальная газовая постоянная [1,6,7,] , то получим уравнение Менделеева - молярная газовая постоянная [2,3,5,15] или универсальная газовая постоянная [1,6,7,] , то получим уравнение Менделеева 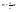 (2.6). Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется (2.6). Уравнение состояния газа часто удобно использовать в записи, предложенной Клапейроном, если количество вещества не изменяется 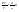 или или  (2.7). Уравнение (2.7) часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества. (2.7). Уравнение (2.7) часто называют обобщённым газовым законом. Тот факт, что из основного уравнения молекулярно-кинетической теории идеального газа можно вывести уравнение состояния идеального газа, подтверждает верность молекулярно-кинетической теории вещества.Основное уравнение молекулярно – кинетической теории газов. Возьмем сосуд с газом и определим давление P газа на стенки сосуда. Для простоты рассмотрения выберем этот сосуд в форме куба с ребром l и расположим его в декартовой системе координат, как показано на рисунке. Пусть в сосуде имеется всего N молекул. Предположим, что:
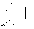 Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона. Импульс силы, полученный стенкой при ударе молекулы, определим из второго закона Ньютона. 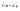 . где . где  - изменение импульса молекулы, m – масса молекулы. Поскольку масса стенки намного больше массы молекулы, то - изменение импульса молекулы, m – масса молекулы. Поскольку масса стенки намного больше массы молекулы, то 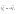 и и 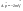 или по модулю или по модулю 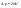 , где использовано обозначение , где использовано обозначение 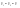 . Таким образом, одна молекула одна молекула за время t передает стенке импульс силы . Таким образом, одна молекула одна молекула за время t передает стенке импульс силы 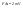 , а за время , а за время 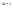 сек передаёт стенке импульс силы равный сек передаёт стенке импульс силы равный 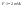 , где k – число ударов молекул за 1 сек. , где k – число ударов молекул за 1 сек. 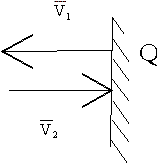 Так как Так как 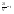 - промежуток времени между двумя последовательными ударами,. то - промежуток времени между двумя последовательными ударами,. то 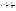 , тогда , тогда 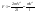 . Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек . Теперь подсчитаем суммарный импульс силы, который передают стенке N1 молекул, движущихся вдоль оси x, за 1 сек 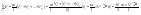 , где скобки < > обозначают среднее значение выражения, стоящего в скобках. Если извлечь корень квадратный из < V2 >, получим среднюю квадратичную скорость молекул, которую будем обозначать <Vкв> , где скобки < > обозначают среднее значение выражения, стоящего в скобках. Если извлечь корень квадратный из < V2 >, получим среднюю квадратичную скорость молекул, которую будем обозначать <Vкв>  - средняя квадратичная скорость молекул газа. Давление, оказываемое газом на грань куба, равно: - средняя квадратичная скорость молекул газа. Давление, оказываемое газом на грань куба, равно: 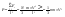 , где n – концентрация молекул. Запишем это выражение в виде , где n – концентрация молекул. Запишем это выражение в виде 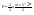 , чтобы подчеркнуть, что в левую часть этого выражения входит средняя кинетическая энергия поступательного движения молекулы , чтобы подчеркнуть, что в левую часть этого выражения входит средняя кинетическая энергия поступательного движения молекулы 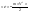 . Тогда . Тогда 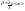 - основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа: - основное уравнение молекулярно-кинетической теории ( уравнение Клаузиуса ) С учетом уравнения состояния идеального газа: 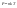 получаем выражение для средней кинетической энергии поступательного движения молекул: получаем выражение для средней кинетической энергии поступательного движения молекул:  - средняя кинетическая энергия поступательного движения молекул. Мы видим, что величина kT есть мера энергии теплового движения молекул. - средняя кинетическая энергия поступательного движения молекул. Мы видим, что величина kT есть мера энергии теплового движения молекул.Газовые законы установлены в 17 веке экспериментально. Однако, их можно получить, используя уравнение Менделеева - Клапейрона. |

 ;
;