Траектория, путь, перемещение. Скорость движения точки по прямой. Нахождение координаты по известной зависимости скорости от времени
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
36. Содержание второго закона термодинамики. Второе начало термодинамики: Невозможно построить периодически действующую тепловую машину, которая бы всю подводимую к ней теплоту превращала в работу, т.е. всегда 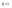 . .Энтропия и второе начало термодинамики Понятие энтропии имеет статистическое толкование. Состояние макроскопического тела (т.е. тела, образованного огромным количеством молекул) может быть задано с помощью объёма, давления, температуры, внутренней энергии и других макроскопических величин. Охарактеризованное таким способом состояние называется макросостоянием. Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется микросостоянием. Всякое макросостояние может быть осуществлено различными способами, каждому из которых соответствует некоторое микросостояние тела. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом  или термодинамической вероятностью макросостояния. В статистической физике существует теорема, которая утверждает о равновероятности всех микросостояний данной системы. В качестве характеристики вероятности состояния можно было бы выбрать статистический вес или термодинамической вероятностью макросостояния. В статистической физике существует теорема, которая утверждает о равновероятности всех микросостояний данной системы. В качестве характеристики вероятности состояния можно было бы выбрать статистический вес  , однако такая характеристика не обладала бы свойствами аддитивности. Поэтому в качестве характеристики состояния принимается величина S, пропорциональная логарифму статистического веса , однако такая характеристика не обладала бы свойствами аддитивности. Поэтому в качестве характеристики состояния принимается величина S, пропорциональная логарифму статистического веса  . .  (4). где (4). где  - постоянная Больцмана. Такую величину называют энтропией. Определённая таким образом энтропия обладает следующими свойствами: - постоянная Больцмана. Такую величину называют энтропией. Определённая таким образом энтропия обладает следующими свойствами:
Эти утверждения и составляют содержание второго начала термодинамики: Энтропия изолированной системы может только возрастать, (либо по достижении максимального значения оставаться неизменной), т.е. 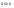 . .37. Неравенство Клаузиуса. Энтропия. Изменение энтропии при обратимых и необратимых процессах. Изменение энтропии в процессах идеального газа. 9.14 Теорема Клаузиуса Рассмотрим обратимый процесс по пути 1а2 и 2б1. Т.к. процессе 1а2б1 обратимый, то для него справедливо равенство Клаузиуса 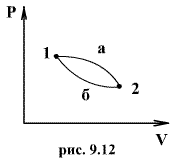 Разобьем этот интеграл на два: по пути 1а2 и 2б1 Поменяем пределы интегрирования второго интеграла или Таким образом, сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса. Разобьем этот интеграл на два: по пути 1а2 и 2б1 Поменяем пределы интегрирования второго интеграла или Таким образом, сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса.Если же 2б1 я-ся необратимым неравновесным способом то ΔS≥0 (интеграл 1а2 больше) неравенство клаузиуса. Изменение энтропии замкнутой системы может либо равняться улю или возрастать для необратимого процесса. 9.15 Энтропия Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно. Мы говорим только об изменении энтропии (подобно изменению потенциальной энергии , для которой не важно где начало отсчета). Из уравнения что выше вытекает основное количественное выражение второго начала термодинамики Энтропия  – это такая функция состояния, дифференциал которой определяется отношением: – это такая функция состояния, дифференциал которой определяется отношением: 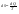 . В СИ энтропия . В СИ энтропия  измеряется в Дж/К. Приведём формулы для подсчёта изменения энтропии в случае изопроцессов для идеального газа: измеряется в Дж/К. Приведём формулы для подсчёта изменения энтропии в случае изопроцессов для идеального газа:а) Изохорический процесс: 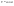 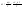 , , 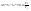 . .б) Изобарический процесс: 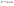 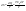 , ,  . .в) Изотермический процесс: 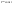 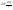 , , 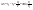 . .г) Адиабатический процесс: 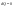 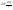 , ,  , ,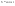 . .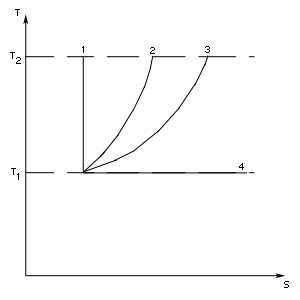  - адиабатический процесс, - адиабатический процесс, - изохорический процесс, - изохорический процесс, - изобарический процесс, - изобарический процесс, - изотермический процесс. - изотермический процесс.38. Энтропия и вероятность. Статистический характер второго закона термодинамики. Третье начало термодинамики. 7.Энтропия. Вероятность. Более глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность Согласно Больцману, энтропия системы и термодинамическая вероятность связаны между собой следующим образом: Энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. В случае необратимых процессов в замкнутой системе энтропия возрастает, т. е. процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной. В случае обратимых процессов энтропия и термовероятность замкнутой системы остаются постоянными. Энтропия системы, находящейся в равновесном состоянии, максимальна. Эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для малых систем может наблюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать или оставаться постоянными. С понижением температуры во всякой системе наблюдается тенденция к упорядоченности. Если бы тело можно было охладить до температуры, равной абсолютному нулю, когда тепловые движения молекул не мешали бы установлению порядка, то в системе установился бы идеальный порядок, которому соответствовала бы минимальная энтропия. Если при абсолютном нуле температуры над системой совершить работу, то энтропия системы не изменится. Это доказано и отражено в теореме Нернста [2]: при абсолютном нуле температуры любые изменения состояния происходят без изменения энтропии. При Т=0 энтропия минимальна S=0. Иногда теорему Нернста возводят в ранг третьего начала термодинамики. Часто третье начало термодинамики формулируют так: абсолютный нуль температуры недостижим. Действительно, если бы существовало тело с Т=0 К (следовательно, S=0), то можно было бы построить вечный двигатель второго рода, что противоречит второму началу термодинамики. 39. Реальные газы. Межмолекулярные силы. При давлении 500 МПа (1 атм=101,3 кПа) объем моле кул составит уже половину всего объема газа. Таким образом, при высоких дав лениях и низких температурах ука занная модель идеального газа непри годна. 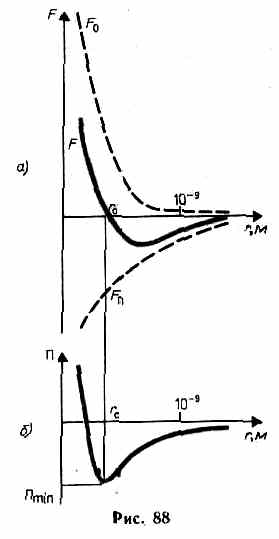 При рассмотрении реальных газов — При рассмотрении реальных газов —газов, свойства которых зависят от взаи модействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях £10-9 м и быстро убывают при увеличении рассто яния между молекулами. Такие силы на зываются короткодействующими. В XX в., по мере развития представле ний о строении атома и квантовой механи ки, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На рис. 88, а приведена качественная зависи мость сил межмолекулярного взаимодей ствия от расстояния r между молекулами, где Fo и Fп— соответственно силы оттал кивания и притяжения, a F— их результи рующая. Силы отталкивания считаются положительными, а силы взаимного при тяжения — отрицательными. На расстоянии r = r0результирующая сила F=0, т. е. силы притяжения и оттал кивания уравновешивают друг друга. Та ким образом, расстояние r0соответствует равновесному расстоянию между молеку лами, на котором бы они находились в от сутствие теплового движения. При r Элементарная работа dA силы Fпри увеличении расстояния между молекула ми на drсовершается за счет уменьше ния взаимной потенциальной энергии мо лекул, т. е. dA=Fdr=-dП. (60.1) Из анализа качественной зависимости по тенциальной энергии взаимодействия мо лекул от расстояния между ними (рис. 88, б) следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимо действия не действуют (г®¥), то П=0. При постепенном сближении молекул между ними появляются силы притяжения (F<0), которые совершают положитель ную работу (dA=Fdr>0). Тогда, со гласно (60.1), потенциальная энергия вза имодействия уменьшается, достигая мини мума при r=r0. При r<r0с уменьшением rсилы отталкивания (F>0) резко воз растают и совершаемая против них работа отрицательна (dA=Fdr<0). Потенци альная энергия начинает тоже резко воз растать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих мо лекул в состоянии устойчивого равновесия (r=r0) обладает минимальной потенци альной энергией. 40. Уравнение Ван - дер - Ваальса. График уравнения Ван - дер - Ваальса. Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Для одного моля газа ( = 1) уравнение изотермы можно представить в виде 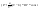 , (4). если считать температуру Т постоянной. Перепишем уравнение (4) в виде , (4). если считать температуру Т постоянной. Перепишем уравнение (4) в виде 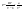 (5). (5). При высоких температурах последний член в (5) можно опустить, и тогда изотерма будет гиперболой, асимптотами которой являются изобара Р = 0 и изохора V = b . Для исследования изотерм при любых значениях Т умножим уравнение (4) на V2. После раскрытия скобок уравнение изотермы примет вид 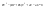 (6) (6)Это уравнение третьей степени по V , в которое давление Р входит в качестве параметра. Поскольку его коэффициенты вещественны, уравнение имеет либо один вещественный корень, либо три корня. Каждому корню на плоскости (V,P) соответствует точка, в которой изобара Р = const пересекает изотерму. В первом случае, когда корень один и точка пересечения будет одна. Так будет, как мы видели, при любых давлениях, если температура достаточно высока. Изотерма имеет вид монотонно опускающейся кривой MN.  При более низких температурах и надлежащих значениях давления Р уравнение (6) имеет три корня V1, V2, V3 . В таких случаях изобара P = const пересекает изотерму в трех точках L, C, G (рис. 1). Изотерма содержит волнообразный участок LBCAG. Она сначала монотонно опускается вниз (участок DB), затем на участке BA монотонно поднимается вверх, а за точкой A снова монотонно опускается. При некоторой промежуточной температуре три корня V1, V2, V3 становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма FKH всюду монотонно опускается вниз, за исключением одной точки K, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка K называется критической точкой. Соответствующие ей давление Pk , объем Vk и температура Tk называются также критическими. Говорят, что вещество находится в критическом состоянии, если его объем и давление (а следовательно, и температура) равны критическим. При более низких температурах и надлежащих значениях давления Р уравнение (6) имеет три корня V1, V2, V3 . В таких случаях изобара P = const пересекает изотерму в трех точках L, C, G (рис. 1). Изотерма содержит волнообразный участок LBCAG. Она сначала монотонно опускается вниз (участок DB), затем на участке BA монотонно поднимается вверх, а за точкой A снова монотонно опускается. При некоторой промежуточной температуре три корня V1, V2, V3 становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма FKH всюду монотонно опускается вниз, за исключением одной точки K, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка K называется критической точкой. Соответствующие ей давление Pk , объем Vk и температура Tk называются также критическими. Говорят, что вещество находится в критическом состоянии, если его объем и давление (а следовательно, и температура) равны критическим.Для нахождения критических параметров Pk, Vk, Tk учтем, что в критической точке уравнение (6) переходит в уравнение 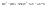 (7). (7).Поскольку в этом случае все три корня совпадают и равны Vk , уравнение должно приводиться к виду 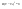 (8). (8). Возводя в куб и сравнивая коэффициенты уравнений (7) и (8), получим три уравнения 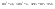 . .Решая их, найдем выражения для параметров критического состояния вещества: 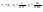 (9). (9).К тем же результатам можно прийти, заметив, что критическая точка К является точкой перегиба изотермы, касательная в которой горизонтальна, а поэтому в точке К должны соблюдаться соотношения 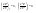 . .Решая эти уравнения совместно с уравнением изотермы (4) придем к формулам (9). Не все состояния вещества, совместимые с уравнением Ван-дер-Ваальса, могут быть реализованы в действительности. Для этого необходимо еще, чтобы они были термодинамически устойчивы. Одно из необходимых условий термодинамической устойчивости физически однородного вещества состоит в выполнении неравенства 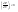 . Физически оно означает, что при изотермическом увеличении давления объем тела должен уменьшаться. Иными словами, при возрастании V все изотермы должны монотонно опускаться. Между тем, ниже критической температуры на изотермах Ван-дер-Ваальса имеются поднимающиеся участки типа BCA (рис. 1). Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут. При переходе к практическим изотермам эти участки должны быть выброшены. . Физически оно означает, что при изотермическом увеличении давления объем тела должен уменьшаться. Иными словами, при возрастании V все изотермы должны монотонно опускаться. Между тем, ниже критической температуры на изотермах Ван-дер-Ваальса имеются поднимающиеся участки типа BCA (рис. 1). Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут. При переходе к практическим изотермам эти участки должны быть выброшены.Таким образом, реальная изотерма распадается на две ветви EGA и BLD , отделенные друг от друга. Естественно предположить, что этим двум ветвям соответствуют различные агрегатные состояния вещества. Ветвь EA характеризуется относительно большими значениями объема или малыми значениями плотности, она соответствует газообразному состоянию вещества. Напротив, ветвь BD характеризуется относительно малыми объемами, а следовательно, большими плотностями, она соответствует жидкому состоянию вещества. Мы распространяем, следовательно, уравнение Ван-дер-Ваальса и на область жидкого состояния. Таким путем удается получить удовлетворительное качественное описание явления перехода газа в жидкость и обратно. Возьмем достаточно разреженный газ при температуре ниже критической. Исходное состояние его на диаграмме PV изображается точкой E (рис. 1). Будем сжимать газ квазистатически, поддерживая температуру T постоянной. Тогда точка, изображающая состояние газа, будет перемещаться по изотерме вверх. Можно было думать, что она достигает крайнего положения A , где изотерма обрывается. В действительности, однако, начиная с некоторой точки G , давление в системе перестает повышаться, и она распадается на две физически однородные части, или фазы: газообразную и жидкую. Процесс изотермического сжатия такой двухфазной системы изображается участком GL горизонтальной прямой. При этом во время сжатия плотности жидкости и газа остаются неизменными и равными их значениям в точках L и G соответственно. По мере сжатия количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе - увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние. Эндрюс систематически исследовал ход изотерм углекислоты (СО2) при различных температурах и на основе этих исследований ввел понятие критической температуры. Углекислота им была выбрана сознательно, так как она обладает критической температурой (310 С), лишь незначительно превышающей комнатную, и сравнительно невысоким критическим давлением (72,9 атм). Оказалось, что при температуре выше 310 С изотермы углекислоты монотонно опускаются вниз, т.е. имеют гиперболический вид. Ниже этой температуры на изотермах углекислоты появляются горизонтальные участки, на которых изотермическое сжатие газа приводит к его конденсации, но не к увеличению давления. Таким путем было установлено, что сжатием газ можно превратить в жидкость только тогда, когда его температура ниже критической. При специальных условиях могут быть реализованы состояния, изображаемые участками изотермы GA и BL. Эти состояния называются метастабильными. Участок GA изображает так называемый пересыщенный пар, участок BL - перегретую жидкость. Обе фазы обладают ограниченной устойчивостью. Каждая из них может существовать до тех пор, пока она не граничит с другой более устойчивой фазой. Например, пересыщенный пар переходит в насыщенный, если в него ввести капли жидкости. Перегретая жидкость закипает, если в нее попадают пузырьки воздуха или пара. |
