ОПД.Ф.7 Статистика. Требования гос впо к обязательному минимуму содержания основной образовательной программы подготовки специалиста
 Скачать 0.94 Mb.
|
|
Тема: «Выборочные наблюдения» Задание 5 № 1 Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5-% выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении – 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определить пределы, в которых будет находиться срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования более 60 дней. № 2 Произведено выборочное наблюдение для определения доли брака продукции. В выборке было взято 400 единиц изделий из общего количества в 4 тыс. единиц. В результате выборки обнаружен брак в 65 изделиях. Определить: размеры колебаний брака во всей партии с вероятностью 0,93; сколько продукции должно быть выборочно обследовано для определения доли брака с ошибкой, не превышающей 1%, исходя из приведенных выше показателей. №3 На ткацкой фабрике работает 800 ткачих. В порядке случайной повторной выборки определена средняя дневная выборка 100 ткачих. В итоге этого обследования получены следующие данные
На основании приведенных данных, определите среднюю ошибку репрезентативности при определении средней дневной выработки ткачих. Какова была бы предельная ошибка репрезентативности при р=0,91 при бесповторном отборе. №4 Для определения среднего возраста мужчин, вступающих в брак, и доли мужчин, вступающих в повторный брак, была произведена 5-% выборка, результаты которой приведены в таблице.
С вероятностью 0,954 определите пределы, в которых будет находиться средний возраст мужчин, вступающих в брак, и долю мужчин, вступающих в брак во второй раз. №5 Произведено выборочное наблюдение для определения доли брака продукции. В выборку было взято 900 единиц изделий из общего количества в 5 тыс. единиц. В результате выборки был обнаружен брак в 70 изделиях. Определить: численность бракованных единиц продукции во всей партии с вероятностью 0,937; сколько продукции должно быть обследовано в порядке выборки для определения доли брака с ошибкой не превышающей 1 %, исходя из приведенных выше показателей, с вероятностью 0,92. № 6 Произведено выборочное обследование длительности производственного стажа рабочих. В выборке было взято 200 рабочих из общего количества в 1000 человек. Результат выборки следующий.
На основании приведенных данных определить: с вероятностью 0,917 возможные пределы колебаний средней продолжительности стажа всех рабочих; какое число рабочих надо взять в выборку, чтобы ошибка не превышала 1 года, на основе приведенных выше показателей. № 7 При обработке материалов учета городского населения методом случайного бесповторного отбора было установлено, что в городе 10% жителей - в возрасте свыше 60 лет. При этом из общей численности города (400 тыс. человек) выборкой было охвачено 100 тыс. человек. Определите, с вероятностью 0,954, в каких пределах колеблется доля жителей в возрасте старше 60 лет среди всего населения города. №8 В процессе случайной выборки было проведено 90 тыс. измерений деталей. В итоге проверки установлено наличие 100 случаев брака. Определите: ошибку репрезентативности при установлении процента бракованных деталей с вероятностью 0,676 и 0,942; пределы, в которых находится процент бракованной продукции. №9 Выборочным обследованием было охвачено 10000 пассажиров пригородных поездов. На основании этого обследования установлена средняя дальность поездки пассажира 40 км. и среднее квадратичное отклонение - 6 км. Определить возможные пределы средней дальности поездки пассажиров при вероятности 0,663, 0,854, 0,947. №10 В городе проживает 10 тыс. семей. С помощью выборки предполагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2. Методические указания к заданиям 1 и 2 Средними величинами в статистике называют обобщающие показатели, выражающие типичные, характерные для определенных условий места и времени размеры и количественные соотношения явлений общественной жизни. В статистике различают несколько видов средних величин, а именно: арифметическую, гармоническую, геометрическую и др. В зависимости от частоты повторения вариант средние исчисляются как простые невзвешенные, так и взвешенные. Среднюю арифметическую невзвешенную рассчитывают по формуле:  ,В задании 1 вид и форма средней выбирается исходя из экономического содержания исчисляемого показателя. Так, например, средняя урожайность определяется отношением валового сбора к посевной площади. Если в условии задачи по бригадам (хозяйствам и т.п.) имеются данные об урожайности и посевной площади, то исходя из экономического содержания показателя для определения средней урожайности применяется средняя арифметическая взвешенная:  где  - значение осредняемого признака (урожайность), - частота (посевная площадь),n- число единиц совокупности. Средняя гармоническая невзвешенная определяется по формуле  Если же в условии даны показатели об урожайности культуры и ее валовом сборе, то для расчета средней урожайности применяется формула средней гармонической взвешенной:  где  - сумма значений осредняемого признака по группе (валовый сбор); - значение осредняемого признака (урожайность).Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине заданного признака, т.е. когда суммированию подлежат не сами варианты, а обратные им величины. Аналогичен подход для расчета средней цены, среднего процента выполнения плана, средней производительности труда и т.п. Средняя геометрическая определяется по формуле  Наиболее широкое применение средняя геометрическая получила для определения среднегодовых темпов роста в рядах динамики. Как сказано выше, при выборе того или другого вида средней следует исходить из того, что средняя применена правильно тогда, когда она имеет реальный экономический смысл. Разновидностью средней являются мода и медиана. Эти величины также используются в качестве характеристик вариационного ряда. Мода (М0) - варианта, встречающаяся в изучаемой совокупности чаще всего, т.е. варианта, которой соответствует наибольшая частота. Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой располагается наибольшая частота, и будет модой. В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Поэтому в модальном интервале необходимо определить модальную варианту. При этом надо иметь в виду, что при расчетах будет получено не точное, а некоторое условное значение моды, так как неизвестен характер распределения частоты внутри модального интервала. Вычисление моды в интервальном ряду производится по следующей формуле: 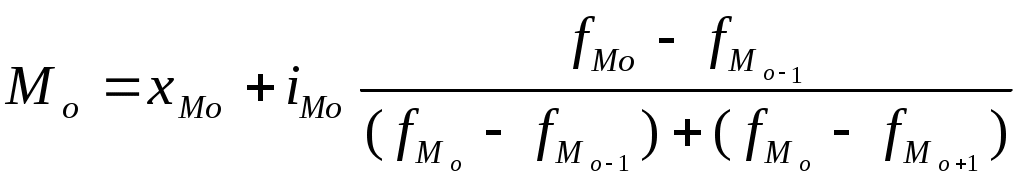 ,где хМо - начало (нижняя граница) модального интервала (15); i - величина интервала (2); fМо - частота модального интервала (30); f Мо-1 - частота интервала, предшествующего модальному (20); f М0+1 - частота интервала, следующего за модальным (25). Воспользуемся данными табл. 1.1. и рассчитаем моду:  Медиана (Ме)- варианта, находящаяся в средине ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Срединная варианта и будет являться медианой. Расчет медианы для интервального ряда производится по формуле  ,где хМе - начало (нижняя граница) медианного интервала (15); i- величина интервала (2);  - сумма накопленных частот ряда (100);sМе-1 - накопленная частота вариант, предшествующих медианному (35); fМе - частота медианного интервала (30). Воспользуемся данными табл. 1.1. и рассчитаем медиану. В табл. 1.1. Ме лежит между 50 и 51 частотами, а они находятся в сумме накопленных частот, равной 65, поэтому интервал 15-17 является медианным. Определяем медиану  Для характеристики размеров колеблемости признаков в статистике применяется следующие показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации и др. Размах вариации представляет собой разность между наибольшим (хmax) и наименьшим (xmin) значениями вариант, т.е. R=хmax-хmin Например, размах вариации производительности труда рабочих в бригаде (см. табл. 1.1) равен: 21-9=12 дет. в смену. Среднее линейное отклонение (  ) определяется из отношения суммы, взятой по абсолютной величине (без учета знака) отклонения всех вариант от средней арифметической, к объему всей совокупности. Оно бывает незвешенное и взвешенное и определяется соответственно по формулам: , ,Дисперсия  - это средняя из квадратов отклонений значений признака от его средней арифметической величины. Она определяется по формуле средней арифметической простой: или средней арифметической взвешенной   Если имеются два взаимоисключающих друг друга варианта, то вариация признака называется альтернативной. Обозначая наличие признака - 1, а отсутствие - 0, и долю вариантов обладающих данным признаком - p, а долю вариантов, не обладающих им - q и замечая, что p+q=1, получаем среднюю:  Дисперсию альтернативного признака определяем по формуле:  Следовательно, дисперсия альтернативного признака  Среднее квадратичное отклонение - это корень квадратный из дисперсии определяется по формулам средней арифметической простой:  или средней арифметической взвешенной 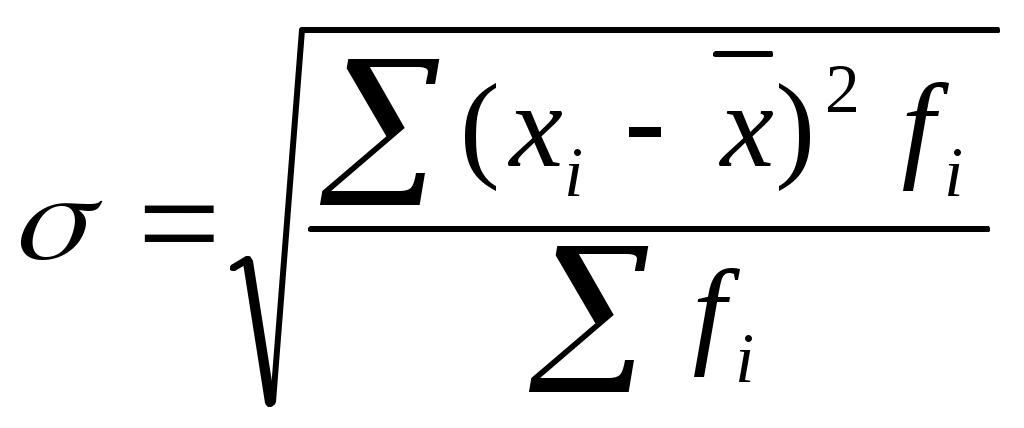 Среднее квадратическое отклонение альтернативного признака:  Мерой сравнения степеней колеблемости для двух, трех и более вариационных рядов служит показатель, который носит название коэффициента вариации и определятся по формуле:  Результаты расчета средней и показателей вариации студент должен представить в таблице по форме табл. 1. Таблица 1 - Пример определения средней и показателей вариации
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
