Требования к компьютерным сетям

• Название: Требования к компьютерным сетям
• Дата: 03.02.2022
• Размер: 259 Kb.
• Имя файла: 41-51.doc
• Тип: Документы; #350408
• страница: 3 из 3

Логико-вероятностные методы анализа надежности систем

Сущность логико-вероятностных методов заключается в использовании функций алгебры логики (ФАЛ) для аналитической записи условий работоспособности системы и переходе от ФАЛ к вероятностным функциям (ВФ), объективно выражающим безотказность системы. Т. е. с помощью логико-вероятностного метода можно описать схемы ИС для расчета надежности с помощью аппарата математической логики с последующим использованием теории вероятностей при определении показателей надежности [2, 3, 8].

Система может находится только в двух состояниях: в состоянии полной работоспособности (у = 1) и в состоянии полного отказа (у = 0). При этом предполагается, что действие системы детерминировано зависит от действия ее элементов, т. е. уявляется функцией х1, х2, … , xi, … , xn. Элементы могут находиться также только в двух несовместных состояниях: полной работоспособности (xi = 1) и полного отказа (xi = 0).

Функцию алгебры логики, связывающую состояние элементов с состоянием системы у (х1, х2,…, xn) называют функцией работоспособности системы F(y) = 1.

Для оценки работоспособных состояний системы используют два понятия:

1)  кратчайшего пути успешного функционирования (КПУФ), который представляет собой такую конъюнкцию её элементов, ни одну из компонент которой нельзя изъять, не нарушив функционирования системы. Такая конъюнкция записывается в виде следующей ФАЛ: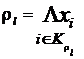

,

где i – принадлежит множеству номеров  , соответствующих данному
l-му пути.

Другими словами, КПУФ системы описывает одно из её возможных работоспособных состояний, которое определяется минимальным набором работоспособных элементов, абсолютно необходимых для выполнения заданных для системы функций.

2)  минимального сечения отказов системы (МСО) представляющего собой такую конъюнкцию из отрицаний её элементов, ни одну из компонент которой нельзя изъять, не нарушив условия неработоспособности системы. Такую конъюнкцию можно записать в виде следующей ФАЛ: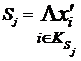

,

где   означает множество номеров, соответствующих данному сечению.

Другими словами, МСО системы описывает один из возможных способов нарушения работоспособности системы с помощью минимального набора отказавших элементов.

Каждая избыточная система имеет конечное число кратчайших путей (l = 1, 2,…, m) и минимальных сечений (j =1, 2,…, m).

Используя эти понятия можно записать условия работоспособности системы.

1)  в виде дизъюнкции всех имеющихся кратчайших путей успешного функционирования.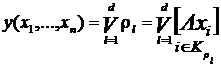

;

2)  в виде конъюнкции отрицаний всех МСО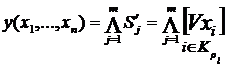

;

Таким образом, условия работоспособности реальной системы можно представить в виде условий работоспособности некоторой эквивалентной (в смысле надежности) системы, структура которой представляет параллельное соединение кратчайших путей успешного функционирования, или другой эквивалентной системы структура которой представляет соединение отрицаний минимальных сечений.

Например, для мостиковой структуры ИС функция работоспособности системы с помощью КПУФ запишется следующим образом: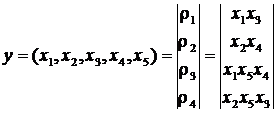

 ;

функцию работоспособности этой же системы через МСО можно записать в следующем виде:



При небольшом числе элементов (не более 20) может быть использован табличный метод расчета надежности, который основан на использовании теоремы сложения вероятностей совместных событий.

Вероятность безотказной работы системы можно вычислить по формуле (через вероятностную функцию вида):



Логико-вероятностные методы (методы: разрезания, табличный, ортогонализации) широко применяют в диагностических процедурах при построении деревьев отказов и определении базисных (исходных) событий, вызывающих отказ системы.

Для надежности компьютерной системы со сложной структурой резервирования может быть использован метод статистического моделирования.

Идея метода заключается в генерировании логических переменных xi c заданной вероятностью pi возникновения единицы, которые подставляются в логическую структурную функцию моделируемой системы в произвольной форме и затем вычисляется результат.

Совокупность х1, х2,…, хn независимых случайных событий, образующих полную группу, характеризуется вероятностями появления каждого из событий p(xi), причем  .

Для моделирования этой совокупности случайных событий используется генератор случайных чисел, равномерно распределенных в интервале [0-1]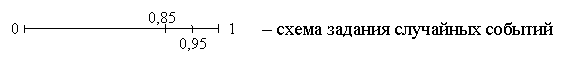



Значение pi выбирается равным вероятности безотказной работы i-й подсистемы. При этом процесс вычисления повторяетсяN0 раз с новыми, независимыми случайными значениями аргументов xi (при этом подсчитывается количество N(t) единичных значений логический структурной функции). Отношение N(t)/N0 является статистической оценкой 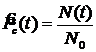 вероятности безотказной работы

,

где N(t) – количество безотказно работающих до момента времени t объектов, при их исходном количестве.

Генерирование случайных логических переменных xi с заданной вероятностью появления единицы рi осуществляется на основании равномерно распределенных в интервале [0-1] случайных величин, получаемых с помощью стандартных программ, входящих в математическое обеспечение всех современных компьютеров.
48)Модель оценки надежности, описываемая системой дифференциальных уравнений

Метод дифференциальных уравнений. Метод применяется для оценки надежности восстанавливаемых объектов и основан на допущении о показательных распределениях времени между отказами (наработки) и времени восстановления. При этом параметр потока отказов w = λ =1/tcp. и интенсивность восстановления µ = 1/tв, где tcp. – среднее время безотказной работы, tв – среднее время восстановления.

Для применения метода необходимо иметь математическую модель для множества возможных состояний системы S = {S1,S2,…, Sn}, в которых она может находиться при отказах и восстановлениях системы. Время от времени система S скачком переходит из одного состояния в другое под действием отказов и восстановлений ее отдельных элементов.

При анализе поведения системы во времени в процессе износа удобно пользоваться графом состояний. Граф состояний – это направленный граф, где кружками или прямоугольниками изображают возможные состояния системы. Он содержит столько вершин, сколько различных состояний возможно у объекта или системы. Ребра графа отражают возможные переходы из некоторого состояния во все остальные с параметрами интенсивностей отказов и восстановлений (около стрелок показаны интенсивности переходов).

Каждой комбинации отказовых и работоспособных состояний подсистем соответствует одно состояние системы. Число состояний системы n = 2k, где k – количество подсистем (элементов).

Связь между вероятностями нахождения системы во всех его возможных состояниях выражается системой дифференциальных уравнений Колмогорова (уравнений первого порядка).

Структура уравнений Колмогорова построена по следующим правилам: в левой части каждого уравнения записывается производная вероятности нахождения объекта в рассматриваемом состоянии (вершине графа), а правая часть содержит столько членов, сколько ребер графа состояний связано с этой вершиной. Если ребро направлено из данной вершины, соответствующий член имеет знак минус, если в данную вершину – знак плюс. Каждый член равен произведению параметра интенсивности отказа (восстановления), связанного с данным ребром, на вероятность нахождения в той вершине графа, из которой исходит ребро.

Система уравнений Колмогорова включает столько уравнений, сколько вершин в графе состояний объекта.

Система дифференциальных уравнений дополняется нормировочным условием: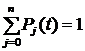

,

где Pj(t) – вероятность нахождения системы в j-м состоянии;

n – число возможных состояний системы.

Решение системы уравнений при конкретных условиях дает значение искомых вероятностей Pj(t).

Все множество возможных состояний системы разбивается на две части: подмножество состояний n1, в которых система работоспособна, и подмножество состояний n2, в которых система неработоспособна.

Функция готовности системы:

Кг ,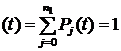

где Pj(t) – вероятность нахождения системы в j работоспособном состоянии;

n1 – число состояний в которых система работоспособна.

Когда необходимо вычислить коэффициент готовности системы или коэффициент простоя (перерывы в работе системы допустимы), рассматривают установившийся режим эксплуатации при t→∞. При этом все производные   и система дифференциальных уравнений переходят в систему алгебраических уравнений, которые легко решаются.

Пример графа состояний нерезервированной восстанавливаемой системы с n – элементами приведен на рис. 1.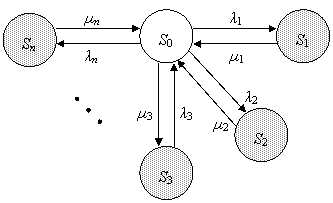



Рис. 1. Граф состояний восстанавливаемой системы (штриховкой отмечены неработоспособные состояния)

Рассмотрим возможные состояния в которых может находиться система. Здесь возможны следующие состояния:

S0 – все элементы работоспособны;

S1 – первый элемент неработоспособен остальные работоспособны;

S2 – второй элемент неработоспособен остальные работоспособны;

.

.

.

Sn – n-й элемент неработоспособен остальные работоспособны.

Вероятность одновременного появления двух неработоспособных элементов пренебрежимо мала. Символами λ1, λ2,…, λnобозначены интенсивности отказов, µ1, µ2,…, µn интенсивности восстановления соответствующих элементов;

По графу состояний (рис. 1) составляют систему дифференциальных уравнений (уравнение для состояния S0 опускаем из-за громоздкости):

С нормировочным условием:  .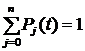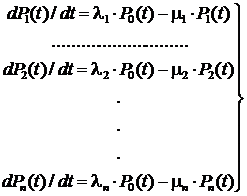



Начальные условия: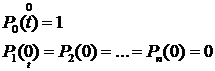



При установившемся режиме эксплуатации (при t→∞) имеем: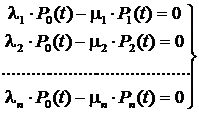



Решив полученную систему алгебраических уравнений с учетом нормировочного условия, находим показатели надежности.

При решении системы уравнений можно использовать преобразование Лапласа для вероятностей состояний или численные методы.
49) Модель оценки надежности, описываемая системой интегральных уравнений

Основной задачей расчета надежности проектируемых ИС является построение математических моделей адекватных вероятностным процессам их функционирования. Эти модели позволяют оценить степень удовлетворения требований по надежности к проектируемым или эксплуатируемым системам.

Вид математической модели определяет возможность получения расчетных формул. Для проведения расчета надежности восстанавливаемых резервированных и нерезервированных систем используются: метод интегральных уравнений, метод дифференциальных уравнений, метод переходных интенсивностей, метод оценки надежности по графу возможных состояний и др. [1, 2, 3, 5, 6].

Метод интегральных уравнений. Метод интегральных уравнений является наиболее общим, его можно применять при расчете надежности любых (восстанавливаемых и невосстанавливаемых) систем при любых распределениях ВБР и времени восстановления.

В этом случае для определения показателей надежности системы составляют и решают интегральные и интегро-дифференциальные уравнения, связывающие характеристики распределения ВБР, а для восстанавливаемых систем – и время восстановления элементов.

В ходе составления интегральных уравнений обычно выделяют один или несколько бесконечно малых интервалов времени, для которых рассматривают сложные события, проявляющие при совместном действии нескольких факторов.

В общем случае решения находят численными методами с помощью компьютера. Метод интегральных уравнений не получил широкого распространения из-за трудности решения
50) Характеристика надежности восстанавливаемых систем

Количественные характеристики надежности (работоспособности) различаются для восстанавливаемых и невосстанавливаемых изделий.

Невосстанавливаемые – те, что не ремонтируются после отказа.

Сложные технические объекты (системы), рассчитанные на длительный срок службы, создаются, как правило, ремонтируемыми. Основные показатели надежности восстанавливаемых объектов (элементов): средняя наработка на отказ; параметр потока отказов; среднее время восстановления; интенсивность восстановления; коэффициенты готовности и оперативной готовности.

Переход системы из неработоспособного (предельного) состояния в работоспособное осуществляется с помощью операций восстановления или ремонта. К первым, в основном, относятся операции идентификации отказа (определение его места и характера), замены, регулирования, заключительных операций контроля работоспособности системы в целом. Переход системы из предельного состояния в работоспособное осуществляется с помощью ремонта, при котором происходит восстановление ресурса системы в целом.

Для восстанавливаемых систем характерно чередование времени исправной работы и времени восстановления (ремонтов).

Система, проработав случайное время t_p1, выходит из строя. После отказа происходит восстановление, и система работает вновь время t_p2 до отказа. Этот процесс продолжается неограниченно. Полагаем, что время восстановления пренебрежимо мало по сравнению со временем работы. Можно считать, что восстановление происходит мгновенно. Отказавший, испорченный элемент немедленно заменяется новым. Элемент после восстановления имеет такую же надежность, что и в начальный момент.

Пусть интервалы времени безотказной работы между двумя соседними отказами распределены по экспоненциальному закону. Тогда вероятность того, что за промежуток времени t в системе произойдет n отказов, определится по формуле Пуассона: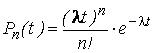

, (n = 0, 1, 2, 3, …),

где λ – среднее число отказов в единицу времени или интенсивность отказов, 
λ = const;

λ = Λ, где Λ – параметр потока отказов. Этот параметр определяется по статистической формуле:

, (12)

где N – общее число отказавших элементов, или число восстановлений, остается неизменным. Отказавшие элементы заменяются новыми.

Поток отказов восстанавливаемой системы является простейшим, пуассоновским.

Параметром потока отказов называется отношение числа отказавших изделий в единицу времени к числу испытываемых изделий при условии, что все вышедшие из строя изделия заменяются исправными (новыми или отремонтированными) Согласно определению ,где – число отказавших образцов в интервале вре­мени от до ; N – число испытываемых об­разцов; – интервал времени.

Для простейшего потока параметр потока отказов определяются по формуле: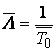

.

Для ремонтируемых объектов удобным для практики критерием надежности является среднее время работы между двумя соседними отказами или наработка на отказ Т₀.

Значения этого параметра определяются по результатам обработки статистического материала, полученного в ходе эксплуатации или экспериментов.

Если устройство проработало суммарное время t_∑ и имело при этом n отказов в работе, то наработка на отказ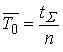

. (13)

Если испытывались N однотипных объектов, то необходимо просуммировать время исправной работы по всем объектам и разделить его на общее число отказов: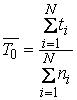

. (14)

Восстановление отказавшего элемента часто требует времени, которым нельзя пренебречь. Среднее время восстановления системы Т_в – это математическое ожидание продолжительности восстановления системы после отказа, т. е. среднее время вынужденного, нерегламентированного простоя, вызванного отысканием и устранением отказа.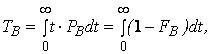

(16)

где Р_в – плотность вероятности времени восстановления;

F_в – функция распределения времени восстановления.

Основной характеристикой восстанавливаемой системы является коэффициент готовности. Коэффициент готовности К_г для установившегося режима эксплуатации определяется как вероятность того, что система будет исправна 
в произвольно выбранный момент в промежутках между плановыми техническими обслуживаниями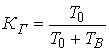

.

Коэффициент вынужденного простоя Кп – это есть отношение времени вынужденного простоя к сумме времени исправной работы и вынужденных простоев:

. (2.20)

Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью:

Kп= 1 -Kг. … (2.21)

Функция готовности есть вероятность того, что в любой момент времени система готова к действию, между функцией и коэффициентом готовности существует зависимость .

51)Интегральный коэффициент готовности