Цены и ценообразование - Есипова В.Е.. Учебник для вузов Издание третье, исправленное и дополненное под редакцией

• Название: Учебник для вузов Издание третье, исправленное и дополненное под редакцией
• Анкор: Цены и ценообразование - Есипова В.Е..doc
• Дата: 03.02.2017
• Размер: 5.7 Mb.
• Имя файла: Цены и ценообразование - Есипова В.Е..doc
• Тип: Учебник; #1903
• Категория: Экономика. Финансы
• страница: 15 из 41

9.2. ОБЩЕЕ РАВНОВЕСИЕ И ЭФФЕКТИВНОСТЬ. ЭКОНОМИКА БЛАГОСОСТОЯНИЯ

Итак, в условиях совершенной конкуренции могут установиться цены, которые обеспечивают равновесие сразу на рынках всех благ и факторов. В соответствии с определениями равновесия это означает, что в сложившейся системе цен все экономические субъекты рыночного хозяйства (как производители, так и потребители) при данной технике и сложившемся распределении доходов не заинтересованы изменять закупки и выпуск продукции.

Означает ли это, что экономика в целом достигла наилучшего из всех возможных своих состояний?

Прежде чем ответить на вопрос, существует ли лучшее, чем общее равновесие, состояние экономики, – нужно решить, что значит улучшение экономического состояния.

По мнению В. Парето^*, любое изменение в экономике, никому не приносящее убытков, но повышающее благосостояние одного или нескольких лиц, является улучшением. Следовательно, оптимальным, по Парето, является такое состояние экономики, при котором нельзя улучшить положение хотя бы одного субъекта, не ухудшая положения других.

^* Вильфредо Парето (1848-1923 гг.), итальянский экономист, социолог и политический деятель
Предположим, что воображаемая экономика состоит только из двух индивидуумов: Федора и Трифона. Если по горизонтальной оси откладывать благосостояние Федора, а по вертикальной – Трифона, то можно построить линию «границы возможных благосостояний» (рис. 9.1). Здесь следует отметить, что изображение конкретного вида границы возможных благосостояний – лишь некоторый возможный вариант для иллюстрации понятия. Дать же точную количественную оценку благосостояния конкретного индивидуума или количественно соизмерить благосостояния разных людей едва ли представляется возможным. Использование понятия «Парето-оптимальность» предполагает возможность определения направления изменения благосостояния отдельных индивидуумов.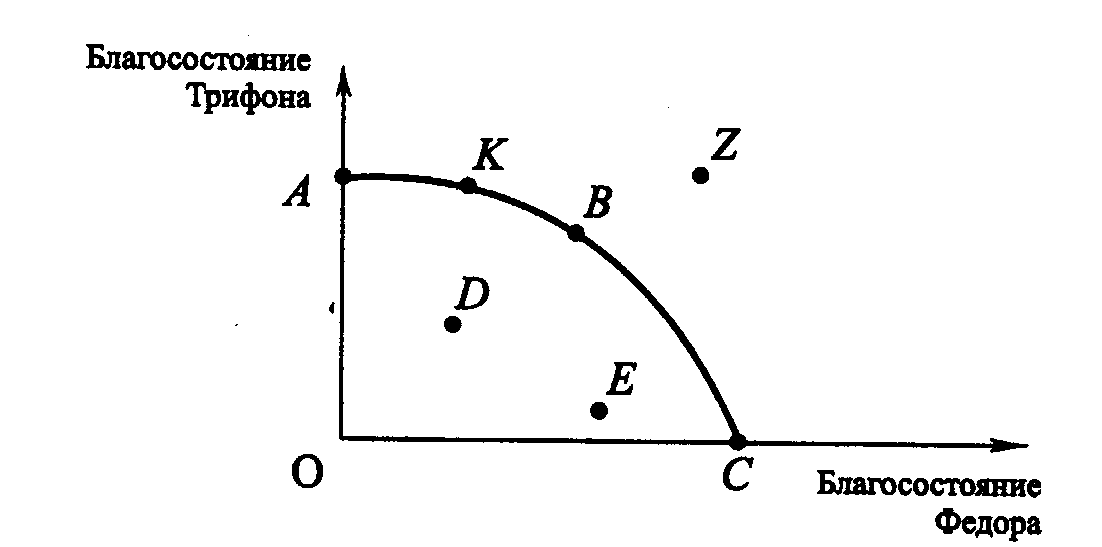


Рис. 9.1. Граница возможных благосостояний

На рис. 9.1 фигура ОАКВС представляет множество возможных благосостояний двух индивидуумов. Чем определяется положение этой линии? Оно определяется наличными производственными ресурсами и характером используемой технологии производства. Если, предположим, увеличилось количество применяемых ресурсов или улучшилась применяемая технология, то это очевидно приведет к сдвигу границы возможных благосостояний вправо вверх, тем самым увеличивается множество возможных доступных благосостояний. Отметим, что при данных условиях, заданном объеме применяемых ресурсов и технологии комбинация двух благосостояний в точке Z является недостижимой. В отличие от Z, благосостояние D достижимо. Но это состояние экономики не является Парето - оптимальным. Почему? Поскольку благосостояние в точках К, В, Е по меньшей мере одного из индивидуумов выше, чем в точке D, а благосостояние другого не ниже. Таким образом, Парето - оптимальными являются все точки, которые лежат на границе АКВС.

Может ли граница возможных благосостояний иметь иную конфигурацию, чем та, которая изображена на рис. 9.1?В принципе – да. Рассмотрим рис. 9.2. На нем граница возможных благосостоянии изображена линией ABCDE. Парето - оптимальному состоянию экономики соответствуют точки на отрезках ВС и DE, то есть только точки, находящиеся на выпуклых участках границы возможных благосостояний.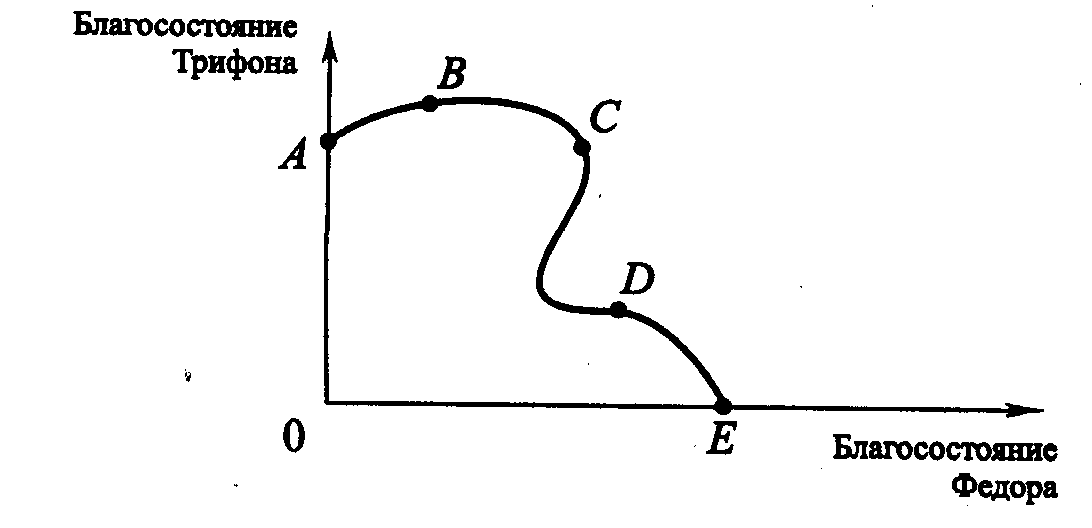


Рис. 9.2. Возможная конфигурация границы возможных благосостояний
Введем понятие «Парето-предпочтительность». Состояние экономики L называется Парето - предпочтительным по отношению к состоянию Т, если в состоянии L благосостояние хотя бы у одного индивидуума выше, а у всех остальных не ниже, чем в состоянии Т. На рис. 9.1 точки К, В, Е являются Парето - предпочтительными по отношению к точке D. Однако точка К не является таковой по отношению к точке Е. При этом точка К является Парето - оптимальной, а точка Е – нет. Одновременно точка Е не является Парето - предпочтительной по отношению к точке К. Вообще, не ко всякой паре состояний экономики может быть применено отношение Парето-предпочтительности. Это отношение применимо лишь в случае, когда данную пару точек в пространстве благосостоянии двух индивидуумов можно соединить отрезком с неотрицательным наклоном. Понятие «Парето-оптимальность» связано с понятием «Парето-предпочтительность». Парето-оптимальное состояние экономики может быть определено как такое, по отношению к которому среди достижимых состояний экономики нет ни одного, обладающего Парето - предпочтительностью.

Эти понятия нужны нам в микроэкономическом анализе, прежде всего, потому, что они в явной форме учитывают несовпадение интересов различных экономических агентов: то, что хорошо для одного, может быть плохо для другого, и наоборот. Они позволяют упорядочить по предпочтительности достижимые состояния экономики. Проиллюстрировать это можно следующим образом: например, если один хозяйственный механизм приводит экономику в состояние В (рис. 9.1), а другой – в D, то совершенно очевидно преимущество первого над вторым. Одно из требований к построению хозяйственного механизма заключается в том, что он должен приводить экономику в Парето-оптимальное состояние или близкое к нему. Нетрудно заметить, что Парето-оптимальных состояний бесконечно много – ими являются все точки, которые принадлежат линии АКВС. Определение же лучшего из данного набора относится к сфере общественного выбора. Однако микроэкономическая теория разрабатывает способы перевода экономики из Парето - оптимального состояния, но «социально несправедливого» состояния, такого как, например, в точке К на рис. 9.1, всостояние, близкое к точке В, которое является «более справедливым», поскольку в точке К Трифону много лучше, чем Федору, который купается в роскоши.

Необходимыми условиями Парето - оптимального состояния являются: эффективность в распределении, эффективность в производстве, эффективность структуры выпуска продукции. Рассмотрим эти условия более подробно.

9.2.1. ЭФФЕКТИВНОСТЬ В РАСПРЕДЕЛЕНИИ (ЭФФЕКТИВНОСТЬ В ОБМЕНЕ)

Состояние экономики называется эффективным в распределении благ между индивидуумами, когда невозможно перераспределить блага таким образом, чтобы благосостояние хотя бы одного из потребителей увеличилось без уменьшения благосостояния других при условии фиксированности объемов производства благ.

Заметим, что определения Парето-оптимальности и Парето-эффективности в распределении благ между потребителями совпадают с той лишь разницей, что во втором определении объемы потребительских благ предполагаются заданными и возможно лишь перераспределять фиксированные объемы благ между потребителями. Эффективность в распределении благ является необходимым, но недостаточным условием Парето-оптимальности.

Для возможности графической иллюстрации будем полагать, что в экономике имеются только два вида продуктов, Х и Y, а также два потребителя, Федор и Трифон. Все выводы можно распространить на любое число благ и потребителей.

На рис. 9.3 изображена коробка Эджуорта - Боули ^* для двух потребителей в пространстве двух благ. Коробка Эджуорта - Боули представляет собой две карты безразличия, наложенные друг на друга таким образом, что одна из них повернута на 180°.

^* Названа так в честь Фрэнсиса Эджуорта (1845-1926 гг.) и Артура Боули (1869-1957 гг.), британских экономистов и статистиков.


Рис. 9.3. Коробка Эджуорта-Боули для двух потребителей, Федора и Трифона

По нижней оси O₁Х₁ откладывается количество товара X, которое потребляет Трифон. На верхней оси O₂X₂ откладывается количество этого же товара, но потребляемое уже Федором. Отрезок O₁L, равный по длине отрезку O₂К, соответствует общему фиксированному количеству товара X.

По оси O₁Y₁ откладывается количество товара Y, которое потребляет Трифон. По оси O₂Y₂ – количество товара Y, потребляемое Федором. Аналогично отрезок O₁К, равный по длине отрезку O₂L, соответствует фиксированному общему количеству товара X..

На рисунок нанесены и кривые безразличия этих двух индивидуумов. Для Трифона они выпуклы влево-вниз, а для Федора – вправо-вверх.

Рассмотрим прямоугольник O₁KO₂L. Любая точка в его пределах характеризует распределение двух товаров между Федором и Трифоном. Так, например, точка А соответствует такому распределению, что Трифон потребляет O₁Х₁' товара Х и O₁Y₁' товара Y, а Федор потребляет O₂X₂' товара Х и O₂Y₂' товара Y.

Из рисунка видно, что точка А не является эффективной в распределении благ между Трифоном и Федором. Точка В (как и всякая другая на участке, ограниченном двумя кривыми безразличия, проходящими через точку А) предпочтительнее, чем А, как для Федора, так и для Трифона. Следовательно, Трифон предпочтет комбинацию В комбинации А. Нетрудно заметить, что точка В расположена ниже кривой безразличия Федора, проходящей через А. Следовательно, и Федор предпочитает комбинацию товаров В. Таким образом, если первоначальное распределение товаров между потребителями соответствует точке А, то возможно улучшить положение как Трифона, так и Федора, перераспределив Y'₁Y"₁ единиц товара Y от Трифона к Федору в обмен на Х'₁X"₂ единиц товара X.

Рассмотрим точку С. В этой точке некая кривая безразличия Федора касается кривой безразличия Трифона. Эта точка является эффективной в распределении благ между потребителями. (Нетрудно заметить, что в точке В положение обоих потребителей хуже, чем в точке С.) Почему? В точке взаимного касания кривые безразличия двух потребителей имеют одинаковый наклон. (Ситуация с угловым решением в данном случае не рассматривается.) Поэтому необходимым признаком состояния, эффективного в распределении благ между потребителями, и, следовательно, состояния, оптимального по Парето, является равенство:

MRS^Ф_XY = MRS^Т_XY (9.5)

где MRS^Ф_XY – предельная норма замены благом Х блага Y для Федора;

MRS^T_XY – предельная норма замены благом Х блага Y для Трифона.

Состояние, эффективное в распределении благ между потребителями, не является единственным. Таковыми являются и состояния, соответствующие точкам Е и D (рис. 9.3). Если соединить все точки касания кривых безразличия одной линией, то мы получим контрактную линию ECD. Хотя эти точки и являются эффективными в распределении благ между потребителями, они вовсе не равнозначны для них. Двигаясь по контрактной линии от точки Е к точке D, мы улучшаем положение Трифона, но ухудшаем положение Федора. Условие (9.5) для двух индивидуумов может быть распространено и для любого количества потребителей. Тогда для всех потребителей этих товаров предельная норма замены должна быть одинаковой.

9.2.2. ЭФФЕКТИВНОСТЬ В ПРОИЗВОДСТВЕ

Предположим, что объемы производственных ресурсов фиксированы. Состояние экономики называется эффективным в производстве, если невозможно увеличить производство одного из товаров, не сокращая при этом производства других.

Рассмотрим ситуацию, когда экономика состоит только из двух предприятий. Первое предприятие производит товар X, а второе – товар Y. При этом используются два вида ресурсов: ресурс А и ресурс В.

На рис. 9.4 изображена коробка Эджуорта-Боули для двух предприятий в пространстве двух ресурсов: А и В.


Рис. 9.4. Коробка Эджуорта-Боули для двух предприятий

Рис. 9.4 внешне напоминает рис. 9.3 с той лишь разницей, что по оси O₁A₁ откладывается количество ресурса А для производства блага X, а по оси О₂А₂ – количество ресурса А, используемое для производства Y. Отрезок O₁L, равный по длине отрезку O₂К, соответствует фиксированному общему количеству ресурса А. По оси O₁В₁ откладывается количество ресурса В, применяемое для производства X, а по оси O₂B₂ – количество ресурса В, используемое для производства Y. Отрезок О₁К, равный по длине отрезку O₂L, соответствует фиксированному количеству ресурса В.

Любая точка в пределах прямоугольника O₁KO₂L на рис. 9.4 характеризует распределение ресурсов А и В между двумя предприятиями. Так, точка F соответствует такому распределению ресурсов А и В между двумя предприятиями, что в производстве блага Х используются O₁A'₁ ресурса А и O₁B'₁ ресурса В, в производстве Y используется O₂A'₂ ресурса А и O₂B'₂ ресурса В.

На рисунок нанесены и изокванты этих двух предприятий. Для предприятия, производящего X, они выпуклы влево-вниз, а для предприятия, производящего Y, – вправо-вверх. Рядом с каждой из изоквант указан соответствующий объем выпуска.

Рассмотрим точку F. Распределение ресурсов, соответствующее этой точке, не является эффективным в производстве. Можно обнаружить, что, перераспределив часть ресурса В от предприятия, которое производит X, к предприятию, производящему Y, в обмен на некоторое количество А, можно перейти к другому распределению ресурсов Р, при котором объемы производства и обоих продуктов выше, чем при распределении ресурсов F.

Точка R, в которой некоторая изокванта предприятия, производящего продукт X, касается некоторой изокванты другого предприятия, производящего Y, является эффективной в производстве. Почему? В точке взаимного касания изокванты двух предприятий имеют одинаковый наклон. Поэтому необходимым признаком состояния, эффективного в производстве, и, следовательно, состояния, оптимального по Парето, является равенство:

MRTS^X_AB = MRTS^Y_AB (9.6)

где MRTS^X_AB – предельная норма технической замены ресурсом А ресурса В в производстве X,

MRTS^Y_AB - предельная норма технической замены ресурсом А ресурса В в производстве Y.

Обратим внимание, что состояние, эффективное в производстве, не является единственным. Такими являются состояния, соответствующие точкам Т и S на рис. 9.4. Если соединить все подобные точки линией, то получим контрактную линию TRS. Условие (9.6) для двух предприятий можно распространить на любое количество предприятий и для любого количества ресурсов. Тогда для всех предприятий предельная норма технической замены должна быть одинаковой. Это условие должно выполняться и для всех пар ресурсов.

9.2.3. ЭФФЕКТИВНОСТЬ СТРУКТУРЫ ВЫПУСКА ПРОДУКЦИИ

Предположим, что достигнуты эффективность в распределении благ между потребителями и эффективность в производстве. Структура выпуска продукции называется эффективной, если невозможно увеличить благосостояние хотя бы одного из них, не уменьшая благосостояния других, путем изменения комбинации (структуры) выпускаемой продукции.

Построим на основе рис. 9.4 границу производственных возможностей. На рис. 9.5 по горизонтальной оси ОХ отложим объем производства товара X, по вертикальной оси OY – товара Y. Каждая из точек на контрактной линии (рис. 9.4) является точкой касания двух изоквант. Так, точке R соответствует точка касания изоквант при Х = 70, а Y = 50. Соответствующую точку отметим на рис. 9.5. Точка S является точкой касания изоквант при Х = 80, а Y = 35. Соответственно и ее нанесем на рис. 9.5 и т. д. Таким образом можно получить всю границу производственных возможностей ITRSK. Фигура, ограниченная этой кривой, есть множество производственных возможностей. Любая комбинация объемов Х и Y, принадлежащая этому множеству, достижима. При этом состояние экономики не является эффективным в производстве.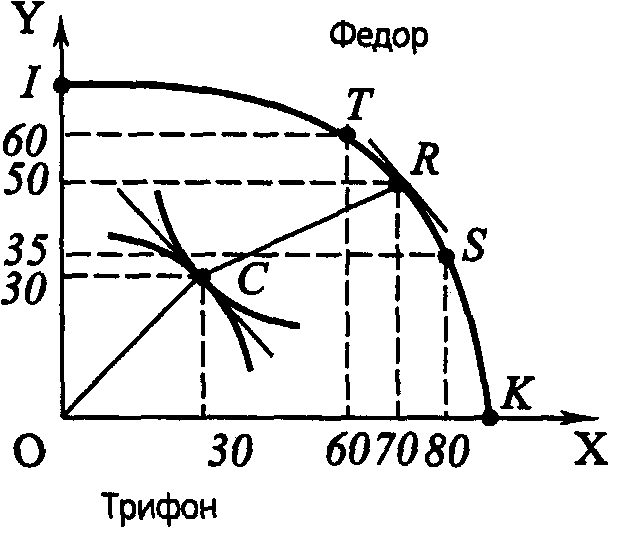


Рис. 9.5. Граница производственных возможностей

Рассмотрим подробнее рис. 9.5. Граница производственных возможностей, изображенная на нем, выпукла вправо-вверх. Это объясняется тем, что одни ресурсы более производительны при производстве одного продукта, а другие ресурсы соответственно при производстве другого. Перемещаясь по границе производственных возможностей вправо-вниз и изменяя структуру выпуска, увеличивая производство X, приходится вовлекать в производство товара Х ресурсы все более неэффективные в производстве данного товара и относительно эффективные в производстве товара Y.

Введем понятие предельной нормы продуктовой трансформации (MRPT_XY). MRPT_XY показывает, каким количеством товара Y следует пожертвовать для производства одной дополнительной единицы товара Х при полном и эффективном использовании всех ресурсов. Геометрически MRPT_XY представляет собой тангенс угла наклона касательной к границе производственных возможностей, взятый с противоположным знаком. (Проведенная через точку R касательная на рис. 9.5 и характеризует MRPT.) Предположим, что в точке R – МRРТ_XY = 1,2.

Теперь сделаем еще один шаг: наложим на множество производственных возможностей коробку Эджуорта-Боули для двух потребителей таким образом, чтобы совместить начало координат для Трифона с точкой О, а начало координат для Федора – с точкой R. Кривая OR представляет собой контрактную линию. Рассмотрим распределение двух благ между потребителями, соответствующее точке С. Это распределение принадлежит контрактной линии. Находясь в этой точке, Трифон из общего количества в 70 единиц блага Х получает 30 единиц блага X, а Федор – 40. Из общего количества блага Y в 50 единиц Трифон получает 30 единиц, а Федор – 20. Как было уже сказано, все точки, принадлежащие контрактной линии, являются точками касания двух кривых безразличия этих потребителей и при этом предельные нормы замены у них равны. Предположим, что в точке С предельные нормы замены для двух кривых безразличия равны 0,6: MRS^Ф_XY = MRS^T_XY = 0,6. Из рисунка видно, что касательная к кривой безразличия, проведенная через точку С, имеет меньший наклон, чем касательная к границе производственных возможностей, которая проведена через точку R.

Таким образом, при объемах производства, соответствующих точке R, и при распределении данной продукции между потребителями, соответствующем точке С, достигается как эффективность в производстве, так и эффективность в распределении. Однако достигается ли при этом Парето-оптимальное состояние? Ответ: нет. Для доказательства этого зафиксируем количество товаров Х и Y, потребляемое Федором. Далее сократим производство Х на единицу. Поскольку MRPT_XY = 1,2, то это позволит увеличить производство Y на 1,2 единицы. А поскольку MRS_XY = 0,6, то Трифон согласится в обмен на сокращение продукта Х на единицу получить дополнительно только 0,6 единиц продукта Y. Его благосостояние при этом не изменится. Если же он получит 1,2 единицы блага Y, его благосостояние повысится. Следовательно, если предельная норма продуктовой трансформации не равна предельной норме замены какого-либо из потребителей, то можно увеличить благосостояние одного из них, не ухудшая положения другого, с помощью изменения структуры выпуска данной продукции. Для данной ситуации это можно сделать, сокращая объем производства блага Х и увеличивая объем производства Y, то есть, двигаясь по границе производственных возможностей (рис. 9.5).

Таким образом, необходимым условием эффективности структуры выпуска продукции, а также Парето-оптимальности является равенство:

MRPT_XY = MRS^T_XY = MRS^Ф_XY. (9.7)

Что произойдет, если мы будем рассматривать модель с n продуктами и m потребителями? Очевидно, что данное равенство (9.7) должно выполняться для любой пары продуктов и для всех потребителей.

Замечание. В данном упрощенном случае мы рассмотрели только три необходимых условия Парето-оптимальности. Если же рассматриваются более сложные ситуации (например, возможность изменения объемов производственных ресурсов), то в этом случае формулируются дополнительные признаки Парето-оптимального состояния.

Поскольку у разных потребителей различные предпочтения благ, то весьма трудно определить, сколько благ нужно произвести и сколько дать каждому потребителю, чтобы у всех была одинаковая MRS? Для этого нужны значительные информационные и материально-технические затраты. Данную проблему проще решить следующим образом.

Если рынки благ являются совершенно конкурентными, все потребители распределят свой бюджет так, чтобы предельные нормы замены по товарам равнялись отношению цен:

(9.8)

В то же время каждая фирма, максимизирующая прибыль, будет продолжать выпуск до тех пор, пока цена не сравняется с предельными издержками, то есть P_X = МС_X и P_Y = МС_Y. Следовательно:

(9.9)

Таким образом, мы показали, что в условиях общего конкурентного равновесия, то есть равновесия на всех рынках в условиях совершенной конкуренции, выполняется эффективность в обмене, эффективность в производстве и эффективность структуры выпуска.

Замечание. В учебниках по математической экономике доказывается, что при весьма общих предложениях общее конкурентное равновесие является одновременно и Парето-оптимальным состоянием.

9.2.4. ДРУГИЕ КРИТЕРИИ ОЦЕНКИ БЛАГОСОСТОЯНИЯ

Для того чтобы рассмотреть несколько весьма полезных критериев, определим, в чем недостаток критерия Парето. Обратимся к рис. 9.6.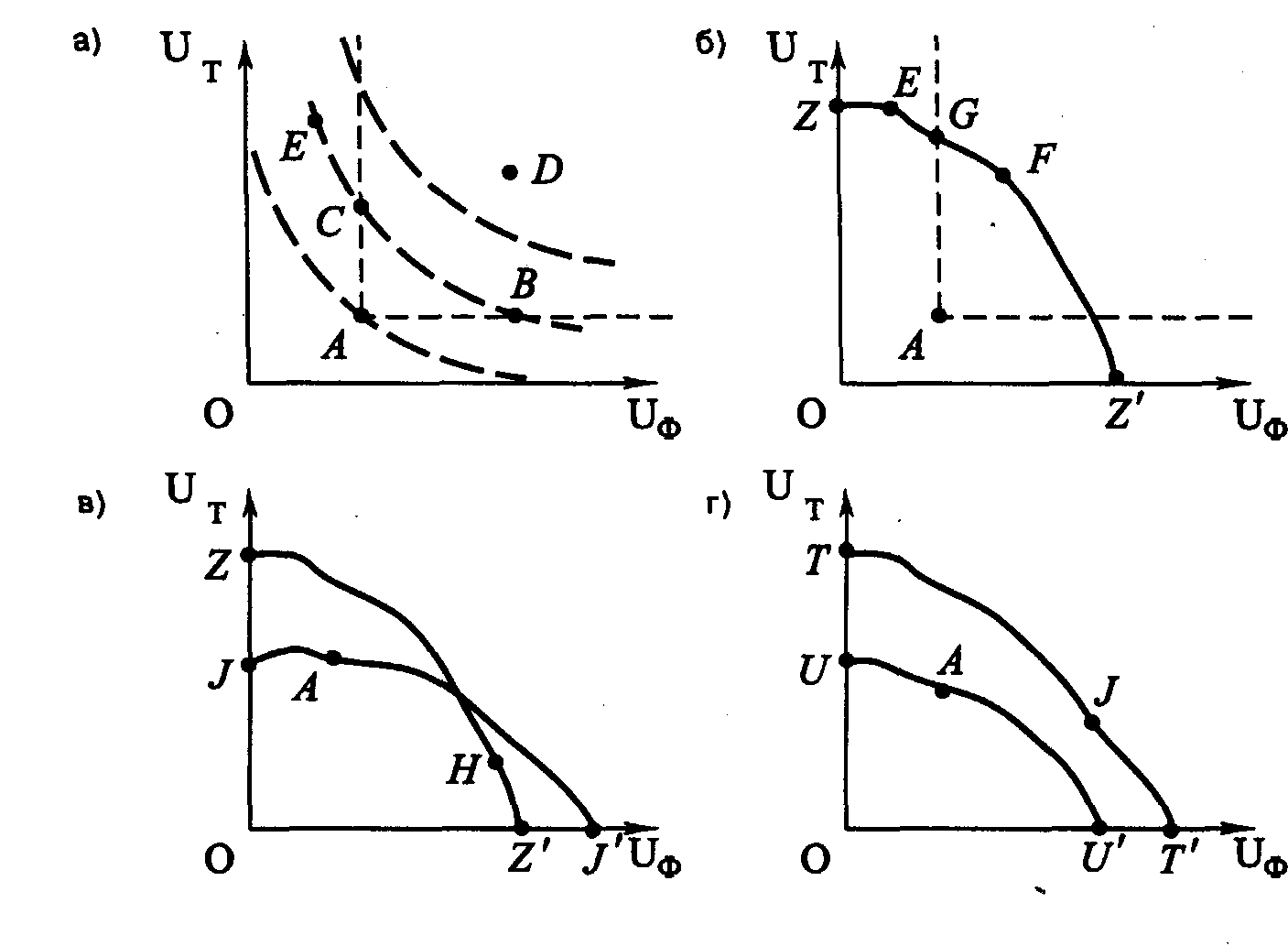


Рис. 9.6. Графическая иллюстрация различных критериев оптимальности

Напомним, что в соответствии с этим критерием любое изменение, которое никому из потребителей не приносит убытков, а кому-то даже пользу, является улучшением. На рис. 9.6, а представлена ситуация с двумя потребителями, Трифоном и Федором: по оси абсцисс откладывается полезность, которую получает Федор (U_Ф), а по оси ординат – Трифон (U_T). В соответствии с критерием Парето, когда состояние характеризуется точкой А, изменение экономической политики улучшает положение, если мы имеем движение по направлению к любой точке (типа В, С, D), которая лежит правее А или выше и правее А, поскольку положение в точке В для Федора лучше, чем в точке А (положение Трифона остается неизменным). Движение же к точке С приносит выгоду Федору, не нанося ущерба Трифону, а движение к точке D приносит выгоды и одному и другому. Однако движение от А к Е нельзя оценивать на основе критерия Парето, поскольку это движение увеличивает благосостояние Трифона, но это происходит за счет снижения благосостояния Федора.

Критерий Калдора. Для объяснения ситуации движения от точки А к точке Е. Н. Калдор^* предложил следующую процедуру. Предположим, что мы спрашиваем у Трифона, какую максимальную сумму он бы уплатил за то, чтобы не отказываться от движения от точки А к точке Е. Предположим, что эта сумма W_T. Аналогичным образом можно выяснить у Федора, сколько он готов уплатить, чтобы предотвратить наступление такого изменения. Обозначим эту сумму через W_Ф. Если W_Ф превышает W_T, Калдор утверждает, что Трифон может компенсировать Федору снижение его благосостояния и при этом сохранить часть выигрыша себе. Итак, изменение является в итоге чистой прибылью (в денежном выражении), поскольку прибыль Трифона превышает убытки Федора. Заметим, что по Калдору не требуется убытки Федора компенсировать так, чтобы никто не оказался бы в проигрыше: индивидуум, получающий прибыль, должен быть способен потенциально осуществить такую компенсацию за свой счет. Вывод Калдора: изменение экономической политики ведет к улучшению, если те, кто выигрывает, оценивают свои доходы выше величины, которую потерпевшие относят к своим убыткам.

^* Николс Калдор (1908-1986 гг.), британский экономист.
Проиллюстрируем критерий Калдора графически (рис. 9.6, б). Введем новую кривую возможной полезности ZZ', характеризующую всевозможные комбинации уровней полезности двух индивидуумов при выполнении условий Парето-оптимальности. Рассмотрим движение из точки F. Посмотрим, что случится, если Федор уступает какую-то часть своего богатства, передавая его Трифону. Мы окажемся в точке G. В этой точке положение Федора хуже, а положение Трифона – лучше, чем в точке F. Двигаясь дальше, мы окажемся в точке Е и т. д. Значит, ZZ' есть геометрическое место точек всех сочетаний уровней полезности для двух индивидуумов, которые могут быть получены через перераспределение богатства между ними и где это перераспределение не сопровождается никакими иными изменениями.

Рассмотрим движение от точки А к точке Е. Это движение нельзя оценить при помощи критерия Парето. ZZ' есть кривая возможной полезности, проходящая через точку Е. Заметим, что имеются и другие точки (например, F и G), к которым можно перейти из Е путем перераспределения богатства. Эти точки лежат выше точки А. По критерию Калдора, движение от точки А к точке Е является улучшением, так как в точке Е можно таким образом перераспределить богатство, что в результате изменения никто не понесет убытков. (Видно, что убыток, который несет Федор, компенсирован в точке G и особенно в точке F). Подводя итоги, отметим, что движение от точки А к точке Е является улучшением в том случае, если А лежит ниже кривой возможной полезности, проходящей через точку Е.

Двойной критерий Т. Сцитовски. Американский экономист Т. Сцитовски^* заметил, что критерий, предложенный Калдором, имеет серьезные недостатки. По этому критерию, возможно, что движение от точки А к точке Н (рис. 9.6, в) означает, что возможно улучшение положения, но в то же время движение от Н к А будет также улучшением. Точка А лежит ниже кривой возможной полезности ZZ', которая проходит через точку Н, но в то же самое время Н лежит ниже кривой возможной полезности JJ', проходящей через точку А. (Такая ситуация возникает в случае пересечения двух кривых возможной полезности.)

^* Тибор Сцитовски (1910 г.) – американский экономист.
Для того чтобы разрешить данную проблему, Сцитовски предложил следующий критерий: а) использовать критерий Н. Калдора для того, чтобы выяснить, улучшает ли положение одного из индивидуумов движение от первоначальной точки к новой; б) использовать критерий Н. Калдора для того, чтобы удостовериться в том, что обратное движение от новой точки к первоначальной не приведет к ухудшению положения. В соответствии с критерием Сцитовски тогда и только тогда, когда движение от одной точки к другой удовлетворяет обоим утверждениям, оно приведет к улучшению.

Однако как и в случае критерия Калдора, так и в случае критерия Сцитовски предполагается, что производится переход от сопоставления благосостояний отдельных индивидуумов к денежной оценке благосостояния этих индивидуумов.

Заметим, что если кривые возможной полезности никогда не пересекаются, то может возникнуть следующая проблема. В точке J (рис. 9.6, г) положение Федора лучше, а положение Трифона хуже, чем в точке А. Если по критерию Калдора и Сцитовски положение в точке J лучше, чем в точке А, поскольку кривая возможной полезности, проходящей через J, лежит выше А, то нет однозначного повода для такого заключения.

Критерий А. Бергсона. Бергсон ^*, в отличие от Калдора и Сцитовски, считает, что основой для выводов относительно улучшения или ухудшения благосостояния должно быть выявление четких суждений о ценности, которые дают сами индивидуумы. Именно эти суждения дадут возможность экономисту оценить положение. По мнению Бергсона, суждения, устанавливающие, что есть справедливость и благо в распределении, могут быть разработаны экономистами, избирателями, законодательными органами или другими правительственными учреждениями. Такой подход равнозначен построению карты безразличия, дающей оценку различным комбинациям полезности, которые могут доставаться различным членам общества (пунктирные линии на рис. 9.6, а). Такая карта безразличия называется функцией общественного благосостояния, аналогичной по своим свойствам ординалистской функции полезности. Она позволяет экономисту принять определенное решение – является ли предложенное изменение экономической политики улучшением положения или не является. Исходя из такого подхода положение Е на рис. 9. 6, а должно считаться лучшим, чем положение А (изменение от А к Е является улучшением), так как Е лежит на более высокой кривой безразличия этой функции общественного благосостояния.

^* Абрам Бергсон (1914 г.) – американский экономист.