Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов

• Название: Учебник для вузов
• Анкор: Дубровский В.И., Федорова В.Н. Биомеханика.doc
• Дата: 28.01.2017
• Размер: 6.47 Mb.
• Имя файла: Дубровский В.И., Федорова В.Н. Биомеханика.doc
• Тип: Учебник; #922
• страница: 14 из 65

4.5. Динамика движения материальной точки по окружности. Центростремительная и тангенциальная силы. Плечо и момент силы. Момент инерции. Уравнения вращательного движения точки

В данном случае материальной точкой можно считать тело, размеры которого малы по сравнению с радиусом окружности.

В подразделе (3.6) было показано, что ускорение тела, движущегося по окружности, складывается из двух составляющих (см. рис. 3.20): центростремительного ускорения — а_ц тангенциального ускорения а_т, направленных по радиусу и касательной соответственно. Эти ускорения создаются проекциями равнодействующей силы на радиус окружности и касательную к ней, которые называются центростремительной силой (F ) и тангенциальной силой (F_T) соответственно (рис. 4.5).
f_t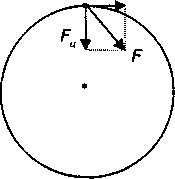



Рис. 4.5. Компоненты равнодействующей силы при неравномерном вращательном движении

Центростремительной силойназывается проекция равнодействующей силы на тот радиус окружности, на котором в данный момент находится тело.

Тангенциальной силойназывается проекция равнодействующей силы на касательную к окружности, проведенную в той точке, в которой в данный момент находится тело.

Роль этих сил различна. Тангенциальная сила обеспечивает изменение величины скорости, а центростремительная сила вызывает изменение направления движения. Поэтому для описания вращательного движения записывают второй закон Ньютона для центростремительной силы:
F_ц=т·а_ц.

(4.11)

Здесь т — масса материальной точки, а величина центростремительного ускорения определяется по формуле (4.9).

В ряде случаев для описания движения по окружности удобнее использовать не центростремительную силу (F_ц), а момент силы, действующей на тело. Поясним смысл этой новой физической величины.

Пусть тело вращается вокруг оси (О) под действием силы, которая лежит в плоскости окружности.

Кратчайшее расстояние от оси вращения до линии действия силы (лежащей в плоскости вращения) называется плечом силы(h).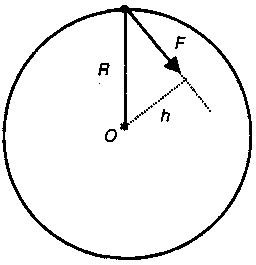


Рис. 4.6. Плечо силы (h)
На рис. 4.6 показаны действующая сила и ее плечо.

Моментом силы(М) относительно оси вращения называется произведение величины силы на ее плечо:

M = ±F·h. (4.12)
Момент силы берется со знаком «+», если сила стремится повернуть тело по часовой стрелке и со знаком «—» в противном случае.

Примечание. В некоторых случаях момент силы считают вектором, направленным по оси вращения. В данном учебнике такие случаи не рассматриваются.

Можно показать, что угловое ускорение (ε), с которым материальная точка движется по окружности, прямо пропорционально моменту (М) действующей на него силы:



Величина, входящая в знаменатель формулы (4.13), называется моментом инерции.

Моментом инерции(J) материальной точки относительно оси вращения называется произведение ее массы (т) на квадрат расстояния (R) до оси вращения:

J = m·R². (4.14)
Из определения следует, что измеряется момент инерции в кг·м².

Подставив момент инерции (4.14) в знаменатель формулы (4.13), получим уравнение описывающее вращение материальной точки под действием силы:

Угловое ускорение материальной точки равно отношению момента действующей на нее силы к моменту инерции точки относительно оси вращения.

Глава 5 ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛА

5.1. Центр масс тела. Масса тела

Любое тело можно рассматривать как совокупность материальных точек, в качестве которых можно, например, брать молекулы. Оказывается, что законы Ньютона, представленные в предыдущем разделе для материальной точки, почти без изменений применимы и к реальному телу, если ввести новое понятие — центр масс (ЦМ).

Пусть тело состоит из п материальных точек с массами m_1, т₂,... т_п.

Центром масс тела, состоящего из п материальных точек, называется точка (в геометрическом смысле), радиус-вектор которой определяется формулой:



Здесь— радиус-вектор точки с номером i(i= 1,2,... п).

Это определение выглядит непривычно, но на самом деле оно дает положение того самого центра масс, о котором у нас имеется интуитивное представление. Например, центр масс стержня будет находиться в его середине.

Применение формулы (5.1) для тела, состоящего из двух точек с массами т и 2т, проиллюстрировано на рис. 5.1.

Можно показать, что скорость и ускорение центра масс определяются аналогичными формулами: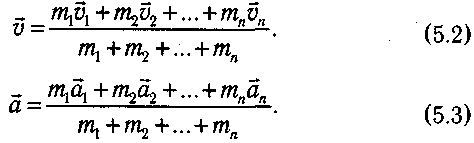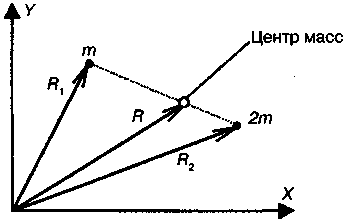





Рис. 5.1. Положение центра масс тела из двух точек

Сумма масс всех точек, входящая в знаменатели формул (5.1-5.3), называется массой тела.

Массой тела называется сумма масс всех его точек:
т = т₁+пц+... + т_п. (5.4)
Центры масс некоторых однородных пластин правильной формы показаны на рис. 5.2.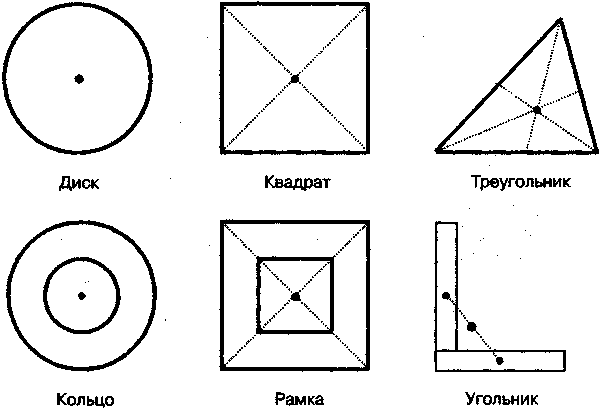



Рис. 5.2. Положение центра масс некоторых пластин правильной формы
В симметричных однородных телах ЦМ всегда расположен в центре симметрии или лежит на оси симметрии, если у фигуры центра симметрии нет. Центр масс может находиться как внутри тела (диск, треугольник, квадрат), так и вне его (кольцо, угольник, квадрат с вырезом в центре). Для человека положение ЦМ зависит от принятой позы. На рис. 5.3. показано положение ЦМ тела прыгуна в воду на различных этапах прыжка. В зависимости от положения частей тела относительно друг друга его ЦМ находится в разных точках.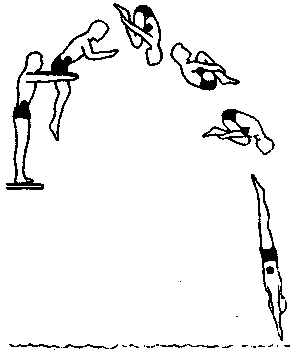



Рис. 5.3. Положение ЦМ прыгуна в воду