Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов
 Скачать 6.47 Mb. Скачать 6.47 Mb.
|
|
Таблица 17.9 Амплитуда движений различных частей тела
Таблица 17.10 Зоны досягаемости человека, см
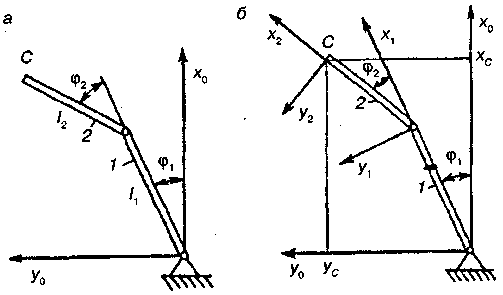 Рис. 17.44. Модель нижней конечности человека: а — расчетная схема, б — кинематическая расчетная схема Обобщенные координаты задают как функцию времени по результатам экспериментальных наблюдений. Решение обратной задачи кинематики представляют интерес для медицины и спорта. Формальная постановка обратной задачи кинематики требует решения уравнения: A1A2… Аi = Вi (17.1) По заданной матрице Вi необходимо найти обобщенные координаты gi. Матричное уравнение (17.1) эквивалентно шести скалярным уравнениям. При этом важно число степеней свободы механизма , который модулирует органы человека. 1 Если ω > 6, то число неизвестных обобщенных координат превышает число уравнений и множество решений оказывается бесконечным. 2. Если ω < 6, то число неизвестных меньше числа уравнений. Задача будет иметь решение лишь при некоторых специальных положениях механизма. 3. Если ω = 6, то, приравняв наддиагональные элементы матриц 4·4, стоящих слева и справа в уравнении (17.1), можно получить систему из шести трансцендентных уравнений относительно обобщенных координат gi. Если это решение дает законы изменения обобщенных координат во времени g((t), то, дифференцируя gi (t), можно найти обобщенные скорости gi(t) и обобщенные ускорения gi(t). Однако при этом погрешности расчета велики из-за необходимости использования методов численного дифференцирования. Антропометрические и масс-инерционные характеристики тела человека. Динамика опорно-двигательного аппарата (ОДА) Тело человека представляет собой сложную биомеханическую систему, которая в повседневной жизни может испытывать значительные ускорения, а в спорте высших достижений особенно. При этом возникают усилия, приводящие к нарушению координации движений, травмам и прочим изменениям в тканях ОДА. Исследования движений человека (спортсмена) аналитическими методами механики проводятся с помощью моделей различной сложности, заменяющих ОДА и воспроизводящих действительную картину движений со степенью точности, достаточной для поставленных в процессе исследований задач. Все сочленения звеньев тела можно моделировать геометрически идеальными вращательными шарнирами. Чтобы воспроизвести движения тела человека, в моделях из максимально возможных шести измеряемых движений для каждого твердого звена, когда оно не присоединено к соседним звеньям (трех поступательных и трех вращательных относительно трех координатных осей, фиксированных на соседнем звене), при наложении кинематических связей исключаются все поступательные и остаются лишь вращательные движения, причем нередко допускаются только некоторые вращательные движения из трех возможных. Все оставшиеся вращательные движения составляют степени свободы звеньев. Формула для определения числа степеней свободы ОДА в целом: где п — число степеней свободы; N — число подвижных звеньев в модели тела; i — число ограничений степеней свободы в соединениях-суставах; Рi— число соединений с i ограничениями. При этом Общее число степеней свободы тела человека составляет около 6 • 144 — 5 • 81 — 4 • 33 — 3 • 29 = 240 (A. Morecki et al., 1969), но с полной достоверностью точное число неизвестно в связи с приближенным характером модели. По кинематической схеме модели (см. рис. 17.43), подобно упрощенному скелету руки (см. рис. 17.43, г), легко подсчитать, что в этом примере подвижность руки относительно плечевого пояса оценивается 7-ю степенями свободы. Положение о преодолении избыточных степеней свободы при работе наглядно изображается на кинематической схеме (см. рис. 17.43, а), если момент мышечных сил в каждом суставе разложить на его составляющие по степени свободы (см. 17.43, г). Очевидно, что число этих компонент момента будет равно числу степеней свободы. Различают две задачи динамики. При решении первой задачи считается, что известны законы движения всех звеньев (обобщенные координаты) и определяются суставные моменты и динамические нагрузки в суставах. Этот расчет позволяет оценить прочность, жесткость и надежность исследуемой системы. Вторая задача динамики заключается в определении динамических ошибок — отклонений законов движения от заданных. Известными считаются внешние силы и находятся законы движения. При решении задач динамики необходимо выбрать и обосновать динамическую расчетную схему. Важную роль при их построении играет моделирование воздействий внешних факторов, в том числе трения, материала и др. Затем строят математическую модель, соответствующую динамической расчетной схеме. При построении динамических расчетных схем тела человека актуальным является определение масс-инерционных характеристик (МИХ) сегментов тела: масс, моментов инерции, координат центров масс отдельных сегментов (частей) тела. Границы сегментов набирают таким образом, чтобы внутри сегмента отсутствовала деформация или непроизвольное изменение геометрии масс сегмента. Обычно выделяют следующие сегменты: стопу, голень, бедро, кисть, предплечье, плечо, голову, верхний, средний и нижней отделы туловища. На рис. 17.45 указаны значения моментов инерции основных сегментов 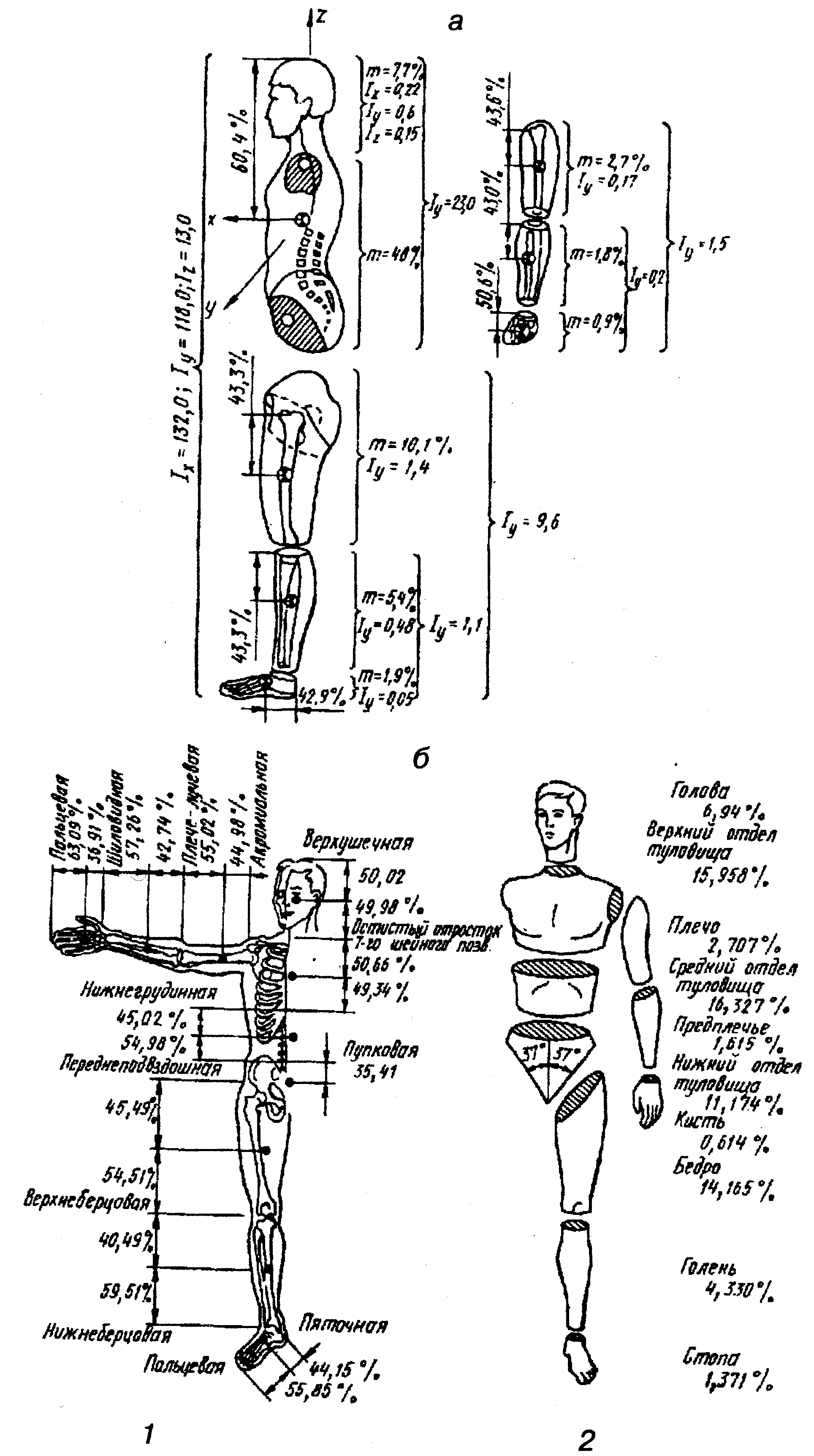 Рис. 17.45. Масс-инерционные характеристики тела человека: а — момент инерции основных сегментов; б — способ разделения на сегменты: 1 — антропометрические точки, определяющие границы сегментов и координаты центров масс сегментов на их продольных осях (в процентах длины); 2 — относительные массы сегментов Таблица 17.11 Коэффициенты уравнений множественной регрессии вида Y = B0 + В1Х1+ В2Х2 для вычисления масс-инерционных характеристик сегментов тела мужчин по весу (Х1) и длине тела (Х2)
Таблица 17.12 Координаты центров масс (рост человека — 100%)
Таблица 17.13 Координаты центров суставов человека, % от роста
(оси обозначены в соответствии с рис.2.1); на рис. 17.45 – антропометрические точки, определяющие границы сегментов и координаты центров масс сегментов на их продольных осях, в табл 17.12 – относительные массы сегментов ( за 100% принята масса тела). Оценку масс-инерционных параметров выполняют как прямыми методами (погружение в воду, внезапное освобождение сечение трупов, компьютерная томография и др.), так и с использованием методов математического и физического моделирования. В последние годы наиболее удобным методом является метод геометрического моделирования. Метод прост для его выполнения необходимы антропометрические измерения (10 обхватов и 10 длин). Минимум ошибок прогнозируется для МИХ отдельных сегментов за счет введения индивидуальных коэффициентов квазиплотности. Кроме этих методов, используют метод определения МИХ по уравнению регрессии, с использованием массы (Х1) и длины тела(Х2) : У =В0 + В1 Х1 + В2 Х2 .Параметры регрессии представлены в табл.17.11. Антропометрические характеристики определяют геометрические размеры тела человека и отдельных его сегментов- это величины, случайным образом измеряющиеся в зависимости от возраста, пола, национальности, рода занятий и т. д. Основные статические, т. е. измерения при фиксированной позе, размеры тела приведены на рис. 17.46, а, и в табл 17.8. Динамические антропометрические характеристики используют для оценки объема рабочих движений, зон досягаемости и в других биомеханических и эргономических задачах, в частности при создании антропометрических манекенов. Некоторые динамические параметры приведены в табл. 17.11; 17.12; 17.13 и на Антропометрическая и инерционная норма Антропометрическая норма определяет связи между линейными размерами любого сегмента тела человека и его ростом Для этой цели введена величина, называемая парсом (П), равная l/56 роста человека. В парсах выражены длины поперечника всех сегментов тела. 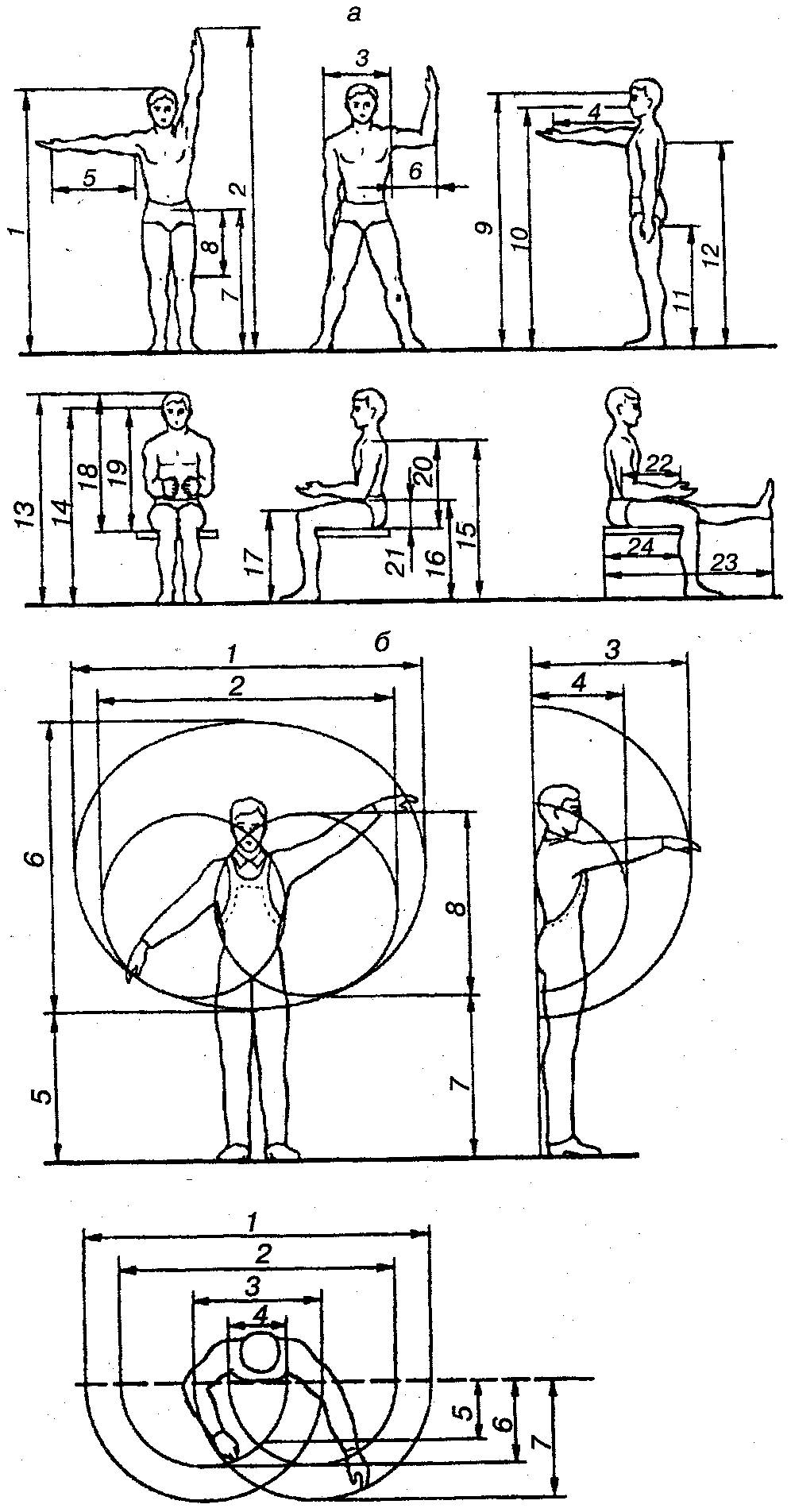 Рис.17.46. Статические характеристики тела человека (а) и зоны досягаемости рук(б) 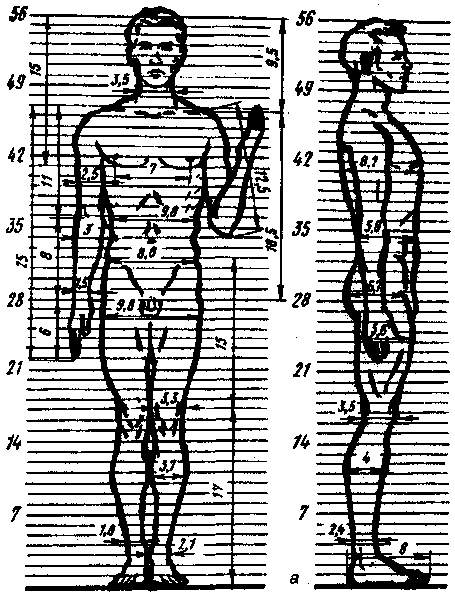 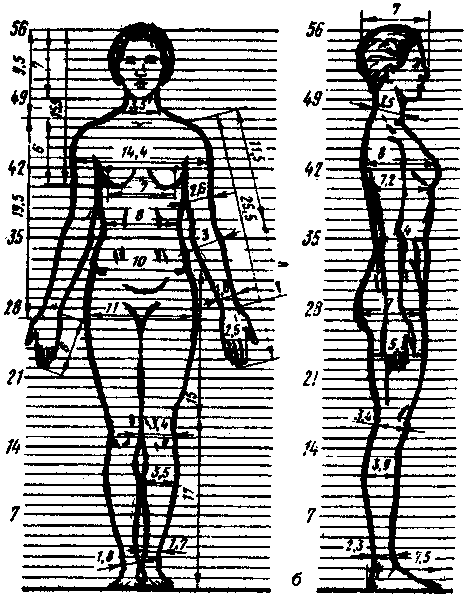 Рис. 17.47. Основные антропометрические характеристики: а — мужчин; б — женщин На рис. 17.47 показаны основные антропометрические характеристики. Ими пользуются, например, для определения длин сегментов после двусторонней ампутации конечностей. На рис. 17.48 буквами обозначены центры суставов, а цифрами — центры масс соответствующих сегментов тела человека (табл. 17.12). При ампутации происходит потеря массы тела, а при параличе — изменение положения центра масс тела. Чем выше уровень ампутации, тем более выражены изменения. Это важно для расчета схем построения протезов и аппаратов для инвалидов. 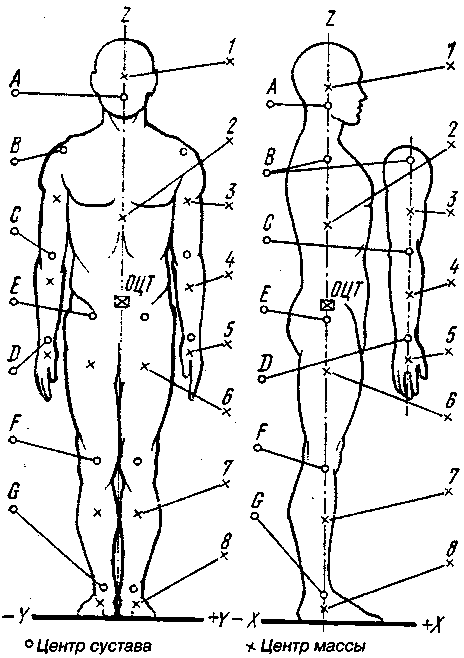 Рис. 17.48. Расположение центров суставов и центров масс в сегментах тела человека | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
