Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов
 Скачать 6.47 Mb. Скачать 6.47 Mb.
|
3.2. Скорость. Средняя и мгновенная скорость. Временные характеристики движенияДля того, чтобы охарактеризовать насколько быстро изменяется в пространстве положение движущегося тела, используют специальное понятие скорость. Средней скоростьютела на данном участке траектории называется отношение пройденного пути ко времени движения: (3.1) Если на всех участках траектории средняя скорость одинакова, то движение называется равномерным. Вопрос о скорости бега является важным в спортивной биомеханике. Известно, что скорость бега на определенную дистанцию зависит от величины этой дистанции. Бегун может поддерживать максимальную скорость только в течение ограниченного времени. Средняя скорость стайеров обычно меньше, чем спринтеров. На рис. 3.8. показана зависимость средней скорости ( V) от длины дистанции (S). 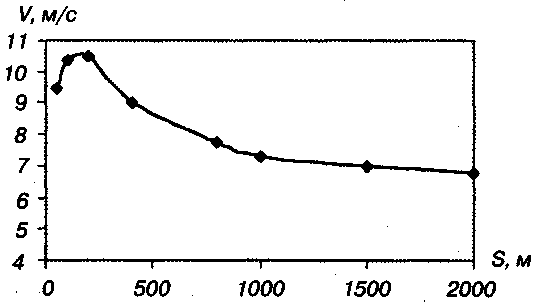 Рис. 3.8. Зависимость средней скорости бега от длины дистанции График зависимости проведен через точки, соответствующие средним скоростям для всех рекордных результатов у мужчин на дистанциях от 50 до 2000 м. Средняя скорость растет с увеличением дистанции до 200 м, а затем убывает. В табл. 3.1 приведены мировые рекорды скорости. Для удобства проведения вычислений среднюю скорость можно записать и через изменение координат тела. При прямолинейном движении пройденный путь равен разности координат конечной и начальной точек. Так, если в момент времени t0тело находилось в точке с координатой x0, а в момент времени t1— в точке с координатой x1 , то пройденный путь Δх = х1— х0, а время движения Δt = t1— t0(в физике и математике принято использовать символ Δ для обозначения разности однотипных величин или для обозначения очень маленьких интервалов). В этом случае (3.2) Таблица 3.1 Мировые спортивные рекорды
В общем случае средние скорости на различных участках пути могут отличаться. На рис. 3.9 представлены координаты падающего тела, моменты времени, в которые тело проходит через эти точки, а также средние скорости для выделенных интервалов. 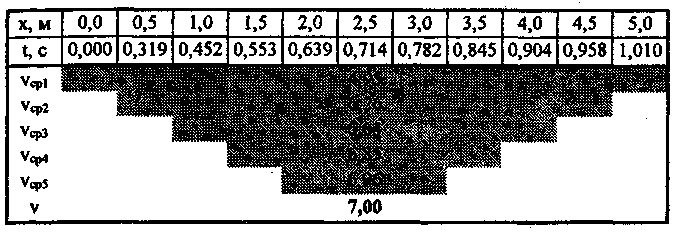 Рис. 3.9. Зависимость средней скорости от участка пути Из данных, приведенных на рис. 3.9 видно, что средняя скорость на всем пути (от 0 м до 5 м) равна Средняя скорость на интервале от 2 м до 3 м равна Движение, при котором средняя скорость изменяется, называется неравномерным. Мы вычисляли среднюю скорость в окрестности одной и той же точки х = 2,5 м. На рис. 3.9 видно, что по мере уменьшения интервала, по которому проводятся вычисления, средняя скорость стремится к некоторому пределу (в нашем случае это 7 м/с). Этот предел называется мгновенной скоростью или скоростью в данной точке траектории. Мгновенной скоростью движения, или скоростью в данной точке траектории называется предел, к которому стремится отношение перемещения тела в окрестности этой точки ко времени при неограниченном уменьшении интервала: Размерность скорости в СИ — м/с. Часто скорость указывают в других единицах (например, в км/ч). При необходимости такие значения можно перевести в СИ. Например, 54 км/ч = 54000 м/3600 с =15 м/с. Для одномерного случая мгновенная скорость равна производной от координаты тела по времени: При равномерном движении величины средней и мгновенной скорости совпадают и остаются неизменными. Мгновенная скорость — величина векторная. Направление вектора мгновенной скорости показано на рис. 3.10.  Рис. 3.10. Направление вектора мгновенной скорости Во время забега мгновенная скорость бегуна меняется. Особенно существенны такие изменения в спринте. На рис. 3.11 приводится пример такого изменения для дистанции 200 м. Бегун начинает движение из состояния покоя и разгоняется, пока не достигнет максимальной скорости. Для бегуна-мужчины время ускорения приблизительно 2 с, а максимальная скорость приближается к 10,5 м/с. Средняя скорость на всей дистанции меньше этого значения. 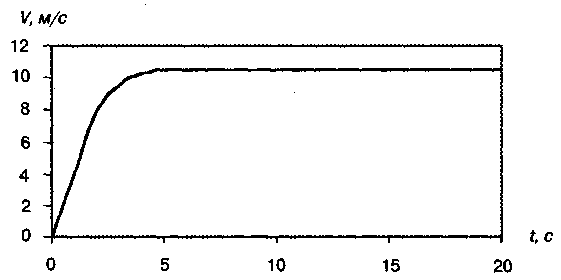 Рис. 3.11. Зависимость мгновенной скорости от времени бега для дистанции 200 м, мужчины Причина того, что бегун не может долго поддерживать свою максимальную скорость движения, состоит в том, что он начинает испытывать недостаток кислорода. Тело содержит кислород, запасенный в мышцах, а в дальнейшем получает его при дыхании. Поэтому спринтер может поддерживать свою максимальную скорость только до тех пор, пока не израсходует запас кислорода. Это кислородное истощение наступает на дистанции около 300 м. Следовательно, для больших дистанций бегун должен ограничивать себя скоростью меньше максимальной. Чем длиннее дистанция, тем меньше должна быть скорость, чтобы кислорода хватило на весь забег. Только спринтеры бегут на максимальной скорости всю дистанцию. На соревнованиях бегун обычно стремиться либо победить соперника, либо установить рекорд. От этого зависит стратегия забега. При установлении рекорда оптимальной стратегией будет та, при которой выбирается скорость, соответствующая полному истощению запаса кислорода к моменту пересечения финиша. В спорте используются специальные временные характеристики. Момент времени(t) — это временная мера положения точки, тела или системы. Момент времени определяют промежутком времени до него от начала отсчета. Моментами времени обозначают, например, начало и окончание движения или какой-либо его части (фазы). По моментам времени определяют длительность движения. Длительность движения(Δt) — это его временная мера, которая измеряется разностью моментов времени окончания и начала движения: Δt = tкон— tнач. Длительность движения представляет собой количество времени, прошедшее между двумя ограничивающими его моментами времени. Сами моменты длительности не имеют. Зная путь точки и длительность ее движения, можно определять ее среднюю скорость. Темп движения(N) — это временная мера повторности движений. Он измеряется количеством движений, повторяющихся в единицу времени (частота движений): В повторных движениях одинаковой длительности темп характеризует их протекание во времени. Темп — величина, обратная длительности движений. Чем больше длительность каждого движения, тем меньше темп, и наоборот. Ритм движений— это временная мера соотношения частей движений. Он определяется по соотношению промежутков времени — длительностей частей движений: Δt2-1 : Δt2-3: Δt4-3... Различный ритм движений для лыжников при скользящем шаге (для пяти фаз шага) показан на рис. 3.12. 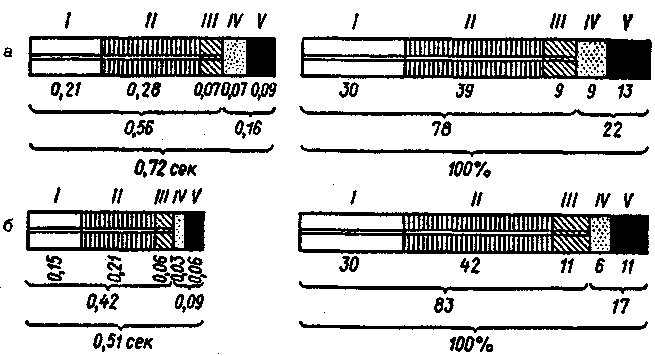 Рис. 3.12. Различный ритм в скользящем шаге на лыжах: а) у высококвалифицированных лыжников; б) у сильнейших лыжников мира; фазы /—/// — скольжение, фазы скольжения, фазы IV— V— стояние лыжи Быстрота— это темп, в котором преодолевается расстояние без учета направления. Быстрота — скалярная величина. Пусть между двумя пунктами при движении по одному шоссе одновременно движутся автомобилист, мотоциклист, велосипедист, бегун. У всех четверых одинаковы траектории, пути, перемещения. Однако их движение отличается быстротой (стремительностью), для характеристики которой и вводится понятие «скорость». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
