логика Гетманова. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики

• Название: Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
• Анкор: логика Гетманова.doc
• Дата: 26.06.2018
• Размер: 2.45 Mb.
• Имя файла: логика Гетманова.doc
• Тип: Учебник; #20763
• страница: 19 из 25

§ 4. ОПРОВЕРЖЕНИЕ ГИПОТЕЗ
Опровержение гипотез осуществляется путем опровержения (фальсификации) их следствий. При этом может обнаружиться, что многие или все необходимые следствия рассматриваемой гипотезы не имеют места в действительности. Кроме того, воз­можно, будут найдены факты, противоречащие выведенным сле­дствиям.

Опровержение гипотез происходит в форме отрицающего мо­дуса (modus tollens) условно-категорического умозаключения, имеющего форму:Этот модус всегда дает достоверное заключение.

Структура опровержения гипотезы такова:
Если имела место причина (гипотеза) Н, то должны быть следствия: С₁ и С₂, и С₃, ..., и С_n.

Суждение, что есть следствие С₁или С₂, или С₃,..., или С_n, является ложным.

_________________

Тогда ложна Н.
В символической логике это умозаключение можно записать таким способом: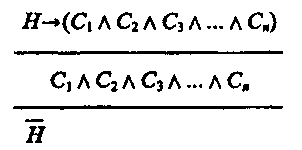



В данном умозаключении мы пользуемся законом де Моргана:

в котором дизъюнкция берется нестрогая. Это означает, что могут отсутствовать одно, два, три или все ηследст­вий. Поэтому для наглядности и удобства практического исполь­зования структуру опровержения гипотез путем опровержения (фальсификации) ее следствий лучше записать таким образом: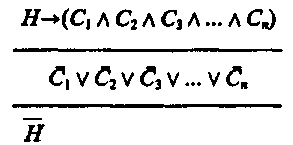

При более точном выражении эта структура опровержения совпадает по формуле не с правилом modus tollens, имеющим только одно основание и одно следствие, а с простой деструктив­ной дилеммой, или трилеммой, или полилеммой, в зависимости от того, сколько следствий вытекает из данной гипотезы: два, три или более.

Приведем пример опровержения гипотезы, из которой выте­кают шесть следствий, т. е. пример простой деструктивной поли­леммы.
Если человек болен крупозным воспалением легких, то у него будет высокая температура (39—40°), сильный озноб, частый сухой кашель, боли в боку, одыш­ка, общее тяжелое состояние.

У данного больного нет высокой температуры (39—40°), или нет сильного озноба, или нет частого сухого кашля, или нет болей в боку, или нет одышки, или общее состояние больного не является тяжелым.

_________________________________________________________

Этот человек не болен крупозным воспалением легких.
Чем большее число следствий отсутствует, тем выше степень опровержения высказанной гипотезы. Если бы в приведенном примере отсутствовало лишь одно или два следствия, то нельзя было бы сделать вывод, что человек не болен крупозным вос­палением легких. Здесь опровергаемые (фальсифицируемые) сле­дствия тоже надо брать по возможности в совокупности. Хотя простое отсутствие следствий (или их необнаружение) не опрове­ргает окончательно гипотезу, так как в данное время, при данных обстоятельствах мы могли их не обнаружить, выдвинутая гипо­теза (или версия) будет подвергнута сомнению. Гипотеза окон­чательно опровергается, если обнаруживаются факты, обстояте­льства, явления, противоречащие вытекающим из данной гипо­тезы следствиям.
§ 5. ПРИМЕРЫ ГИПОТЕЗ, ПРИМЕНЯЮЩИХСЯ НА УРОКАХ В ШКОЛЕ
Велика роль гипотезы в познании. Законы науки и теории до их подтверждения прошли стадию гипотезы. Поэтому учитель, излагая естественно-научные теории, должен показать и стадии, предшествовавшие доказательству теории. Ученые неоднократно подчеркивали огромную роль гипотез. М. В. Ломоносов писал, что гипотезы представляют единственный путь, которым вели­чайшие люди дошли до открытия самых важных истин.

Рассказывая о роли гипотезы в познании, учителя физики и химии смогут привлечь большой и интересный материал из этих наук. Мы проиллюстрируем способ ознакомления учащихся при изучении этих дисциплин в школе лишь некоторыми приме­рами как классических, так и современных гипотез.

На уроках физики учитель будет рассказывать о К. Э. Циол­ковском — основоположнике теории космических полетов. В 1903 г. К. Э. Циолковский опубликовал свою замечательную работу «Исследование мировых пространств реактивными при­борами», которая, по словам академика С. П. Королева, опреде­лила его жизненный и научный путь. В этой работе К. Э. Циол­ковский сформулировал гипотезу: «Центробежная сила уравнове­шивает тяжесть и сводит ее к нулю» — таков путь к космическим полетам. «Вычисления могли указать мне и те скорости, которые необходимы для освобождения от земной тяжести и достижения планет»⁹ (обратим внимание на то, что в качестве фактов К. Э. Циолковский использует результаты математических рас­четов). «Почти вся энергия Солнца пропадает в настоящее время бесполезно для человечества, ибо Земля получает в два (точнее, в 2,23) миллиарда раз меньше, чем испускает Солнце.

Что странного в идее воспользоваться этой энергией! Что странного в мысли овладеть и окружающим земной шар бес­предельным пространством...»¹⁰

На уроках физики учитель приведет научные сведения об успехах в освоении космоса в мирных целях, а также о гелиоэлек­тростанциях, которые, по предположению ученых, смогут кон­курировать с тепловыми и атомными электростанциями.

Учитель также познакомит учащихся с теорией естественной радиоактивности. За открытие радиоактивности (естественных радиоактивных элементов полония и радия) А. Беккерель, П. Кюри и М. Склодовская-Кюри награждены в 1903 г. Нобе­левской премией. После четырех лет упорного труда, перерабо­тав вручную на старом складе более тонны урановой руды, Марии Кюри удалось выделить чистый хлорид радия. Позднее, в 1911 г., за получение металлического радия (совместно с Дебьеном) Мария Кюри получила Нобелевскую премию по химии. Она единственная в мире женщина, дважды удостоенная Нобе­левской премии. Мария Кюри пишет, что изучение физических свойств радиоактивных веществ еще не вполне закончено и что, хотя некоторые главные положения уже установлены, большая часть выводов еще носит гадательный характер. Исследования разных ученых, изучающих эти вещества, постоянно сходятся и расходятся. Эти высказывания М. Кюри свидетельствуют о ги­потезах («гадательный характер») и о появлении конкурирующих гипотез, когда мнения ученых зачастую расходились.

В настоящее время выдвигается целый ряд гипотез относите­льно возможности создания единой теории, которая описывала бы все физические явления, включая явления микромира, мак­ромира и мегамира. Но это дело будущего.

Много примеров выдвижения и подтверждения гипотез дает и история химии. Классический пример — блестящее подтверж­дение периодического закона и Периодической системы химических элементов Д. И. Менделеева, следствием которого явилось предсказание существования еще не открытых тогда элементов, а также того, что значения атомных весов урана, тория, берил­лия, индия и ряда других химических элементов должны быть существенно иными. Впоследствии эти предсказания получили эмпирическое подтверждение. Д. И. Менделееву принадлежат и другие гипотезы: о химической энергии, о пределе химических соединений, о строении кремнеземистых соединений и т. п.

Следует обратить внимание учащихся и на большое количест­во гипотез, которые присутствуют в науках, изучающих организ­мы. Ч. Дарвин в своих исследованиях о происхождении видов опирался на гипотезы, выдвигаемые на основе обобщения значи­тельного числа фактов, полученных им во время 5-летнего путе­шествия на корабле «Бигль».

Карл Линней прошел пешком почти 7000 км по северу Скан­динавии, изучая этот край и собирая фактический материал для построения гипотез и своей искусственной классификации расте­ний. Он посетил многие страны Европы, просмотрел гербарии многих ученых-ботаников, его ученики побывали в Канаде, Егип­те, Китае, Испании, Лапландии и оттуда присылали ему собран­ные растения. Друзья Линнея из различных стран присылали ему семена и высушенные растения. Таков огромный материал, кото­рый послужил Линнею для его систематизации.

Знакомясь с работами И. П. Павлова, учащийся «увидит, как мало-помалу расширялся и исправлялся наш фактический мате­риал, как постепенно складывались наши представления о разных сторонах предмета и как, наконец, перед нами все более и более слагалась общая картина высшей нервной деятельности»¹¹.

Интересны работы Л. Пастера по проблемам болезней вина, в результате которых он пришел к созданию биохимической теории брожения. Одним из следствий этой теории была разработка процесса, названного позже пастеризацией. Огромное практическое значение имело также исследование Пастером болезни шелковичных червей. В результате этой болезни в бедственном положении оказались более 3,5 тыс. владельцев недвижимого имущества шелководческих департаментов Франции. Почти пять лет посвятил Л. Пастер трудным экспериментальным исследованиям и потерял на этом свое здоровье, но тем не менее считал, что был счастлив, так как принес пользу своей стране, изыскивая способы предотвращения страшной нищеты: «...дело чести ученого перед лицом несчастья пожертвовать всем ради попытки помочь от него избавиться. Поэтому, может быть, я дал молодым ученым благотворный пример длительных усилий в разрешении трудной и неблагодарной зада­чи»¹².

На занятиях по биологии кроме этих классических примеров превращения гипотез в теории в результате их подтверждения учитель должен показать и современные биологические гипотезы.

Следует обратить внимание учащихся на то, что многие из них построены на стыке ряда наук. Очень важной является гипотеза о возможности получения значительных урожаев на солончаках, составляющих примерно ²/₃ общей площади культивируемых земель. Поэтому встает общая проблема мирового значения: как превратить пустынные солончаковые земли в сельскохозяйствен­ные угодья? Среди многих других гипотез выдвигается предложе­ние культивировать на этих землях галовиты — растения, устой­чивые к соли. С появлением средств генной инженерии количест­во таких предложений будет увеличиваться и можно предвидеть значительные успехи в целенаправленном изменении многих представителей животных и растений.

Итак, наука развивается посредством выдвижения гипотез. Однако гипотеза имеет и практическое значение.

В юриспруденции и в юридической практике роль гипотез, называемых там версиями, невозможно преувеличить. Любое расследование преступления требует выдвижения всех возмож­ных версий, объясняющих преступление, и их проверки.

В педагогической науке, особенно в методике преподавания математики, физики, химии и других предметов, а также в методи­ке начального обучения, также выдвигаются свои гипотезы о пу­тях более эффективного процесса обучения и воспитания, прово­дятся эксперименты в школах для подтверждения этих гипотез.

В результате приведенных примеров, иллюстрирующих гипо­тезы, используемые в школе на уроках физики, химии, биологии, истории (как классические, так и современные), в практике обуче­ния и воспитания, можно с уверенностью считать, что гипотеза является формой развития знания во всех науках, а также во всех других (а не только научных) отраслях знаний.
Глава VIII РОЛЬ ЛОГИКИ В ПРОЦЕССЕ ОБУЧЕНИЯ
Так как вопросы ставятся не только для решения новых проблем и задач, стоящих перед наукой и практикой, но и в процессе овладевания уже добытыми знаниями, в педагогической работе, в ходе обучения и воспитания школьников и студентов, в процессе полемики, дискуссий, диспутов, рассмотрение роли логики в процес­се обучения мы начинаем именно с логической структуры вопросов.
§ 1. ЛОГИЧЕСКАЯ СТРУКТУРА ВОПРОСА
Вопрос в познании играет особенно большую роль, так как все познание мира начинается с вопроса, с постановки проблемы. Проблемы перед познанием, в том числе перед различными науками, ставит практика, поскольку она выступает в качестве основы познания. В настоящее время практика поставила перед людьми такие проблемы, как получение замедленной термоядер­ной реакции, разработка методов лечения онкологических забо­леваний, решение продовольственной проблемы и многие другие. Нет ни одной сферы трудовой деятельности, где бы не возникали вопросы.

Термины «проблема», «вопрос», «проблемная ситуация» обо­значают нетождественные, хотя и связанные между собой поня­тия. Термин «проблема» означает такой вопрос из области науки, для ответа на который недостаточно имеющейся к данному моменту информации (знания). Гипотеза выступает как одно из возможных решений стоящей проблемы. Вопрос же — форма выражения проблемы. Но вопрос ставится и с целью получения некоторой информации, уже имеющейся у человека, с целью выявления его личного мнения по данному вопросу или с целью обучения. Велика роль вопроса в процессе социологических ис­следований, проводимых в форме интервью, анкетирования, при массовом или выборочном опросе. В процессе передачи все боль­шего числа интеллектуальных функций ЭВМ умение правильно сделать запрос для введения его в ЭВМ, способность четко, корректно сформулировать этот вопрос (запрос) будет содей­ствовать быстрейшему информационному поиску нужных сведе­ний, цифрового материала и др. Велика роль правильной, одно­значной постановки вопросов в судебно-следственной практике.

Педагог В. А. Сухомлинский значительную роль в процессе обучения, в ходе развития логического мышления школьников отводил умению учителя ставить перед учениками вопросы и до­биваться правильных ответов на них, таких ответов, которые способствовали бы интеллектуальному развитию личности уче­ника, будили бы собственную мысль ребенка. Вопросы подбира­лись различные по сложности, многообразные по характеру при­влекаемых учениками знаний при ответе на них, разнообразные по форме, учитывающие возраст учеников.

Для маленьких детей в школе Сухомлинского вывешивали картинки, помогающие осмыслить окружающую действитель­ность. Например, картинки под общим заглавием «Почему это так происходит?». Веточка вербы, воткнутая во влажную почву, дает ростки, превращается в дерево, а веточка дуба засыхает. Почему? Вторая серия картинок — «Зачем так делают?». Напри­мер, зачем зимой в толстом льду пруда делают прорубь? В силь­ную жару пересыхающую почву вокруг овощных растений посы­пают мелким перегноем. Зачем? Картинки третьей серии — «Что здесь неправильно изображено?». На картинке умышленно до­пущены ошибки, например: под густой тенью дуба зреют крас­ные помидоры; тень от тополей падает в ту же сторону, с какой

светит солнце; ульи с пчелами установлены на участке поля, засеянного пшеницей. На одной из картинок четвертой серии — «Где это происходит?» — изображен самолет, садящийся на не­большую площадку, окруженную ледяными торосами. На стенде «Для чего так делают?» под картинками надписи: «Для чего каменный уголь перед сжиганием смачивают водой?»; «Для чего на зиму металлические части машин смазывают маслянистыми веществами?» Серия картинок — «Как узнать?». Будет ли весной цвести яблоня — как узнать об этом зимой? И так далее¹.

Мышление ученика направлено на поиски ответов на воп­росы. Вызвать такую потребность у ученика — это и значит приобщить его к умственному труду. По мнению Сухомлинс­кого, самое трудное и самый верный показатель мастерства педагога — умение ставить вопросы.

Работая директором школы, Сухомлинский ежедневно посе­щал по два урока своих учителей. Изо дня в день слушая ответы учеников, он спрашивал себя: «Почему в ответах часто отсутству­ет живая, собственная мысль ребенка?» — и пришел к выводу: «Мы не учим ребенка мыслить».

Вопрос формулируется в вопросительном предложении, кото­рое не выражает суждения, и, следовательно, оно не истинно и не ложно. Например, «Когда родился композитор Верди?», «Запу­щен ли искусственный спутник Марса?», «Все ли вулканы — го­ры?» и др.

Всякая вопросно-ответная ситуация включает в себя, во-первых, исходную информацию о мире (например, о композиторе Верди, об искусственных спутниках), которая называется базисом или пред­посылкой вопроса, и, во-вторых, указание на ее недостаточность и необходимость дальнейшего дополнения и углубления знаний.

В вопросе «Где был убит заговорщиками Гай Юлий Цезарь?» базисом служит неявно содержащееся в нем утверждение — «Су­ществует х, являющийся местом убийства заговорщиками Гая Юлия Цезаря»².

Вопрос — это логическая форма, включающая исходную, или базисную, информацию с одновременным указанием на ее недоста­точность с целью получения новой информации в виде ответа.
Виды вопросов

Обычно различают два вида (типа) вопросов: I тип — уточняющие (определенные, прямые, или «ли» вопросы).

Например: «Верно ли, что И. С. Васильев успешно защитил кандидатскую диссертацию?»; «Надо ли сдавать вступительный экзамен по иностранному языку на историческом факультете МГУ?»; «Действительно ли в Москве больше жителей, чем в Па­риже?» и др. Во всех этих вопросах присутствует частица «ли», включенная в словосочетания «верно ли», «действительно ли», «надо ли» и т. д.

Уточняющие вопросы могут быть простыми или сложными. Простые вопросы в свою очередь делятся на условные и безус­ловные.

«Верно ли, что космонавты побывали на Луне?» — простой безусловный вопрос.

«Верно ли, что если он сдаст все экзамены на «отлично», то получит повышенную стипендию?» — простой условный вопрос.

Сложные вопросы (как и сложные суждения) делятся на воп­росы конъюнктивные (соединительные) и дизъюнктивные (раз­делительные), включающие в себя строгую или нестрогую ди­зъюнкцию. Каждый сложный вопрос можно разбить на два или несколько простых. Например:

1. «Кто является автором романа «Красное и черное» и рома­на «Пармская обитель»?»

2. «Хотите кофе или чаю?»

3. «Вы пойдете в кино или не пойдете?»

Вопросы вида: «Если будет хорошая погода, то мы поедем на экскурсию?» или «Если «Динамо» выиграет этот матч у «Спарта­ка», то команда «Динамо» выйдет в финал розыгрыша?» — не относятся к сложным вопросам, так как их нельзя разбить на два самостоятельных простых вопроса. Это примеры простых усло­вных вопросов.

II тип вопросов — восполняющие (неопределенные, непрямые, «к»-вопросы, включающие в свой состав вопросительные слова: «где?», «когда?», «кто?», «что?», «почему?», «какие?» и др.). Нево­льно вспоминаются телепередачи о «Клубе знатоков»: «Что? Где? Когда?». Эти вопросы также делятся на простые и сложные. Например, вопросы: «Какой город является столицей Португа­лии?», «Что означает слово «филистер»?» — являются простыми, направленными на поиски недостающего знания, на восполнение недостающей информации.

Сложными восполняющими вопросами являются те, которые можно разбить на два или несколько простых восполняющих вопроса, например: «Кто, где, когда, из какого оружия совершил убийство президента США Джона Кеннеди?», или «Как при увеличении стороны равностороннего треугольника в 2 раза из­меняется его периметр или площадь?», или «Кто является авто­ром поэмы «Дом у дороги» и поэмы «Василий Теркин»?»
Предпосылки вопросов

Предпосылкой, или базисом, вопроса является содержащееся в вопросе исходное знание, неполноту или неопределенность которого требуется устранить. На эту неполноту или неопределенность указывают операторы вопроса, т. е. вопросительные слова: «кто?», «что?», «когда?», «почему?» и др.

Вопросы делятся на логически корректные (правильно постав­ленные), т. е. такие, предпосылки (базисы) которых являются истинными суждениями, и на логически некорректные (или не­правильно поставленные), предпосылки которых — ложные или неопределенные (по смыслу) суждения. Если в основе поставлен­ного вопроса лежит простое незнание спрашивающего о лож­ности базиса, то вопрос некорректен. Если же спрашивающий знает о ложности базиса вопроса и задает вопрос с целью прово­кации, запутывания своего оппонента, то такой вопрос называют провокационным, а его постановка есть софистический прием.

Например, вопрос: «В каком году Р. Амундсен первым до­стиг Северного полюса?» — поставлен неправильно (некоррект­но), так как в базисе этого вопроса содержится предположение, что Р. Амундсен якобы достигал Северного полюса, а спрашива­ющий может не знать, что Р. Амундсен первым достиг в 1911 г. Южного полюса.

Примерами провокационных вопросов являются следующие: «Как построить «вечный двигатель»?», «Перестал ли ты бить своего отца?».

Предпосылки подобных вопросов заведомо ложны, поэтому вопросы эти не просто неправильно поставлены, сама постановка их — софистический прием.
Правила постановки простых и сложных вопросов

1. Корректность постановки вопроса. Итак, вопросы должны быть правильно поставленными, корректными. Провокационные и неопределенные вопросы недопустимы.

2. Предусмотренные альтернативы ответа («да» или «нет») на уточняющие вопросы. Например: «Шел ли вчера в центре Моск­вы дождь?», «Признает ли Ломов себя виновным в предъявлен­ном ему обвинении?»

3. Краткость и ясность формулировки вопроса. Длинные, запутанные, нечеткие вопросы затрудняют их понимание и ответ на них.

4. Простота вопроса. Если вопрос сложный, то его лучше разбить на несколько простых. Например: «Где, когда, в какой семье родился Джеймс Фенимор Купер?» Этот сложный вопрос следует разбить на три простых.

5. В сложных разделительных вопросах необходимость пере­числения всех альтернатив. Например: «К какому виду электро­станций относится данная электростанция: теплоэлектростанция (ее разновидность — атомная электростанция), гидроэлектроста­нция, солнечная или геотермальная?» Здесь нет пятой альтер­нативы — ветровая электростанция.6. Необходимость отличать обычный вопрос от риторического (например, «Кто из вас не любит А. С. Пушкина?»). Риторические вопросы являются суждениями, так как в них содержится утвержде­ние или отрицание, обычные же вопросы суждениями не являются.
Логическая структура и виды ответов

1. Ответы на простые вопросы. Ответ на простой вопрос первого вида (уточняющий, определенный, прямой, «ли»-вопрос) предполагает одно из двух: «да» или «нет». Например, «Является ли Александр Дюма-отец автором романа «Двадцать лет спу­стя»?» (ответ: «да»).

Ответ на простой вопрос второго вида (восполняющий, не­прямой, «к»-вопрос) требует привлечения точной, исчерпыва­ющей информации (о времени, месте, причинах, результатах события, природного явления и других факторах).

2. Ответы на сложные вопросы. Ответ на сложный конъюнк­тивный (соединительный) вопрос требует ответа на все простые вопросы, входящие в сложный. Например: «Верно ли, что настой­ку женьшеня применяют в качестве тонизирующего средства при гипертонии, переутомлении, неврастении?» (ответ: «да», «да», «да»).

При ответе же на сложный дизъюнктивный (разделительный) вопрос часто достаточно дать ответ лишь на один или несколько из составляющих его простых вопросов (на одну альтернативу). Например, на вопрос: «Предпочитаете ли Вы летом путешество­вать или отдыхать у речки?» — ответом будет суждение: «Я предпочитаю летом отдыхать у речки».

В начале параграфа была показана важная роль вопросов в познании. Остановимся на столь же важной роли вопроса в обучении, так как от качества и правильности постановки вопросов в значительной мере зависит усвоение материала и ус­певаемость учащихся.

В процессе обучения можно воспользоваться такой классифи­кацией вопросов. Первый тип вопросов — прямые, на которые можно ответить «да» или «нет», второй — прямые, на которые нельзя дать такого однозначного ответа, и третий — полупря­мые, в которых спрашивается, какое из двух (или большего числа) суждений истинно. В последнем случае сложный вопрос приходится разбивать на несколько простых.

При ответе на вопрос учащийся должен выявить предпосылки вопроса и установить, истинны они или ложны. При ложных предпосылках вопрос должен быть отвергнут как некорректный, т. е. неправильно поставленный, например «Все ли гейзеры — вулканы?».

Корректные вопросы должны вызывать активную мыслитель­ную деятельность учащихся, если в них заключено оптимальное количество неопределенности. Если вопрос содержит слишком большую неопределенность, то он ставит ученика в значительное затруднение. Вопросы «легкие», с малой неопределенностью по­зволяют учащимся ответить словами учебника, не требуют ис­следования, рассмотрения частных случаев.

Например, вместо вопроса: «Сколько окружностей можно провести через три точки, не лежащие на одной прямой?» (легкий ответ — «одну») — лучше поставить такой вопрос: «Существует ли окружность, проходящая через три точки?», — так как готово­го ответа на него в учебнике нет и учащиеся сами должны рассмотреть различные случаи расположения трех точек (на од­ной прямой или не на одной прямой).

Учителю следует избегать постановки неопределенных воп­росов, например: «Что можно сказать о треугольнике АВС ?» , или «Какими свойствами обладает трапеция?», или «Какими свойст­вами не обладают кубы?»
Постановка вопросов в процессе проблемного обучения

Под проблемным обучением понимается такое изучение мате­риала, которое вызывает в сознании учащихся познавательные задачи и проблемы, напоминающие научный поиск³. Разрешение этих проблем активизирует творческие умственные способности учащихся.

В младших классах проблемные ситуации возникают при формулировании загадок, задач на сообразительность и смекал­ку, шарад. Такие проблемные ситуации можно создавать, пред­лагая детям обобщить чувственные данные и сделать вывод. Можно, например, поставить вопрос: «Почему лед, пар, облака называют водой?» Другим примером проблемной ситуации для учащихся младших классов является постановка задачи: постро­ить треугольник по трем заданным углам [специально даются такие углы, сумма которых значительно больше (или меньше) 180°]. Учащиеся не могут выполнить эту задачу и думают над причиной, почему она неразрешима.

В начальных классах перед учащимися можно ставить пробле­мы, направленные на поиски математических закономерностей: 1) изменение суммы в зависимости от изменения одного из сла­гаемых; 2) изменение частного в зависимости от изменения дели­мого или делителя; 3) изменение площади квадрата в зависимо­сти от увеличения или уменьшения в несколько раз его стороны и т. д. Эффективны и отдельные проблемные вопросы типа: «Почему четырехугольник назван четырехугольником? Можно ли было дать ему другое название, также связанное с его свой­ством?» или «Как бы вы назвали треугольник, у которого один угол тупой?»⁴ Учитель в процессе ответа на основной проблем­ный вопрос должен уметь ставить и наводящие вопросы. В процессе обучения математике возникают различные типы задач (стандартная обучающая, поисковая, проблемная). Основ­ными компонентами задачи считают: условие, заключение, реше­ние, обоснование решения, которые могут быть не известны человеку (в частности, школьнику) в момент постановки перед ним данной задачи. Стандартная задача — это такая задача, у которой четко определено условие, известен способ решения и его обоснование и которая представляет собой упражнение на воспроизведение известного. Обучающей является та задача, в ко­торой неизвестен (или плохо определен) один из вышеуказанных основных компонентов. Если неизвестны какие-либо два компо­нента, то задачу называют поисковой, а три — проблемной⁵.

Это деление задач несколько условно, так как в зависимости от уровня знаний и методической подготовки человека она может быть отнесена к тому или иному типу. Например, при изучении темы «Вписанные четырехугольники» учитель ставит перед уча­щимися такую вводную задачу (проблему): «Где расположить центральный штаб туристского слета, чтобы он находился на равных расстояниях от заданных мест расположения четырех туристских групп?»

Точками А, В, С, Dобозначены места расположения групп, а точкой О — предполагаемое место расположения штаба (рис. 45).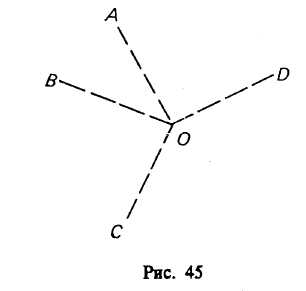



В старших классах школьники в процессе проблемного обуче­ния строят различные гипотезы, намечают способы проверки их истинности, самостоятельно «открывают» правила, законы, формулы, доказывают теоремы.

Общая учебная проблема включает в себя несколько частных учебных проблем. Результаты их решения в своей совокупности позволяют дать окончательное решение общей (главной) пробле­мы. Проблемное обучение включает в себя не только создание проблемной ситуации (постановку проблемного вопроса), но и самостоятельную творческую работу учащихся, открытие но­вых для них закономерностей, свойств, отношений, а также логическое обоснование (доказательство) истинности своих суждений и правильности хода рассуждений при опровержении ложных суждений и неправильных умозаключений. Разумеется, проблем­ный метод обучения нельзя превращать в универсальный; его надо использовать наряду с объяснительным, сообщающим из­ложением материала учителем.