_КР Математика 38.05.02 2016. Учебнометодические указания по выполнению контрольной работы Дисциплина математика
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
2. УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 12.1. Аналитическая геометрия на плоскостиГлавыI, II[1]; № 4, 10, 23, 28 [3]. ГлавыIII § 11, 12 [1], гл. IV №59, 67, 71, 82 (2), 87, 103 [3]. Главы V § 24-26, 30-36 [1]; № 140, 155, 166, 169, 190, 211, 224 [3]. Разберите решения задач 1, 2, 3 из данных методических указаний. Примеры решения задач Задача 1. Даны вершины треугольника АВС: А (−4; 8), В(5; −4), С(10; 6). Найти: 1) Длину стороны АВ. 2) Уравнения сторон АВ и АС и их угловые коэффициенты. 3) Внутренний угол А радианах с точностью до 0,01. 4) Уравнение высоты СD и ее длину. 5) Уравнения окружности, для которой высота СD есть диаметр. 6) Систему линейных неравенств, определяющих треугольник АВС. Решение:1. Расстояние d между точками М1 (х1; y1) и М2 (x2; y2) определяется по формуле: d = 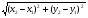 (1) (1)Подставив в эту формулу координаты точек А и В, имеем: АВ = 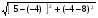 = =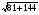 =15 =15
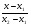 = =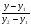 (2) (2)Подставив в (2) координаты точек А и В, получим уравнение прямой АВ: 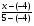 = =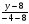 , , 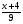 = = 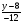 , , 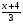 = = 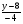 ,3у – 24 = − 4х – 16, 4х + +3у – 8 = 0 (АВ). ,3у – 24 = − 4х – 16, 4х + +3у – 8 = 0 (АВ).Для нахождения углового коэффициента kАВ прямой АВ разрешим полученное уравнение относительно у: у= − 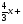 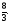 Отсюда kАВ= − Отсюда kАВ= −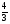 . Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС: . Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС: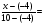 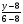 . .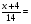 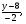 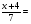 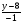 ,х+7у-52=0 (АС). ,х+7у-52=0 (АС).Отсюда kАС = − 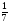 . .
tg 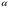 = =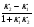 (3) (3)Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее k1=kАВ= − 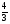 , k 2= kАС=− , k 2= kАС=−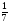 . .tg А = 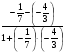 = =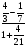 = =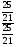 =1, =1,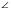 А = arctg 1 = 45° А = arctg 1 = 45°  0,79 рад. 0,79 рад.
у – у1=k(х – х1) (4) Подставив в (4) координаты точки С и kСD= , получим уравнение высоты СD: у – 6 = 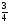 (х – 10), 4у – 24 = 3х – 30, 3х – 4у – 6=0 (CD). Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (CD): (х – 10), 4у – 24 = 3х – 30, 3х – 4у – 6=0 (CD). Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (CD): 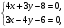 откуда х = 2, у = 0, то есть D (2;0). откуда х = 2, у = 0, то есть D (2;0).Подставив в формулу (1) координаты точек С и D, находим: CD = 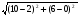 = = 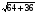 =10. =10.
(х – а)2+(у – b)2 = R2. (5) Так как CD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим: хЕ= 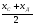 = = 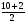 =6, уЕ= =6, уЕ= 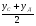 = = 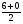 =3. =3.Следовательно, Е (6; 3) и R= 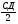 =5. Используя формулу (5), получаем уравнение искомой окружности: (х – 6)2 + (у – 3)2 = 25. =5. Используя формулу (5), получаем уравнение искомой окружности: (х – 6)2 + (у – 3)2 = 25.6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А,а третья ограничена прямой АС и содержит точку В. Для получения неравенства, определяющего полуплоскость, ограниченную прямой, АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С: 4·10 + 3·6 – 8 =50 > 0. Поэтому искомое неравенство имеет вид: 4х + 3у – 8 ≥0. Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С: 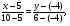 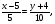 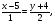 2х – у – 14 =0 (ВС). 2х – у – 14 =0 (ВС).Подставив в последнее уравнение координаты точки А, имеем: 2·(−4)– 8–14=−30<0. Искомое неравенство, определяющее полуплоскость, ограниченную прямой Ас и содержащую точку В: 5+7·(−4)–52=−75<0. Третье искомое неравенство х+7у–52≤0. Итак, множество точек треугольника АВС определяется системой неравенств 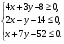 На рис. 1 в декартовой прямоугольной системе координат хОу изображен треугольник АВС, высота СD, окружность с центром в точке Е. 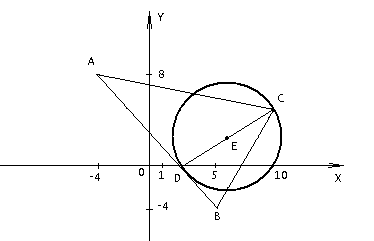 Рис. 2.1. Решение задачи 1 Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки А (3; 0) и до прямой х= 12 равно числу 0,5. Полученное уравнение привести к простейшему виду и построить кривую. Решение. Пусть М (х; у) – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр МВ на прямую х=12 (рис. 2). Тогда В (12; у). По условию задачи 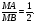 МА= 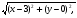 МВ= МВ= 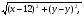 (6) (6)Тогда 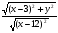 = = 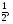 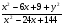 = = 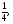 4х2 – 24х + 36 + 4у2 = 4х2 – 24х + 36 + 4у2 == х2 – – 24х + 144, 3х2 + 4у2=108, 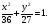 Полученное уравнение представляет собой эллипс вида: 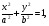 где а=6, b=3. Определим фокусы эллипса F1 (−с; 0) и F2(с; 0). Для эллипса справедливо равенство b2=a2 – b2 =9 и с=3.То есть, F1 ( −3; 0) и F2 (3; 0) – фокусы эллипса (точки F2 и А совпадают).Эксцентриситет эллипса  = = = = 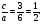 Графически решение задачи 2 представлено на рис. 2.2. Графически решение задачи 2 представлено на рис. 2.2.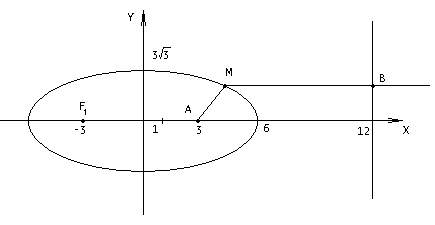 Рис. 2.2. Решение задачи 2 Задача 3. Составить уравнения линии, для каждой точки которой ее расстояние до точки А (3; −4) равно расстоянию до прямой у=2. Полученное уравнение привести к простейшему виду и построить кривую. Решение. М (х; у) – текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у=2 (рис. 3). Тогда В (х; 2). Так как МА =МВ,то 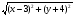 = = 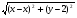 или (х – 3)2+ +у2+8у+16 =у2 – 4у +4,−12у – 12 =(х – 3)2,у +1= − 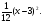 Полученное уравнение определяет параболу с вершиной в точке О' (3; −1). Для приведения уравнения параболы к простейшему (каноническому) виду положим х – 3=Х', у +1=У'. Тогда в системе координат Х'О'У' уравнение параболы принимает следующий вид: У'=− (Х')2. В системе координат Х'О'У' строим параболу (рис. 1.3). 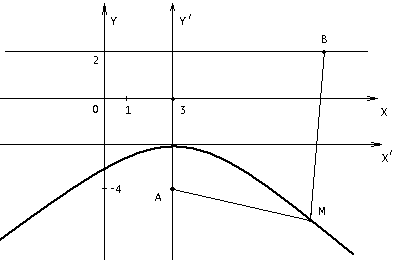 Рис. 2.3. Решение задачи 3. 2.1.1. Вопросы для самопроверки1. Дайте определение прямоугольной декартовой системы координат. 2. Напишите формулу для нахождения расстояния между двумя точками. 3. Напишите формулы для определения координат точки, делящей данный отрезок в данном отношении. 4. Напишите формулы преобразования координат: а) при параллельном переносе системы координат; б) при повороте системы координат. 5. Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через данную точку в данном направлении; в) проходящей через две данные точки; г) в «отрезках». 6. Как найти координаты точки пересечения двух прямых? 7. Напишите формулу для определения угла между двумя прямыми. 8. Каковы условия параллельности и перпендикулярности двух прямых? 9. Сформулируйте определение окружности. 10. Напишите уравнение окружности с центром в любой точке плоскости хОу; с центром в начале координат. 11. Дайте определение эллипса. Напишите каноническое уравнение эллипса. 12. Что называется эксцентриситетом эллипса? Как изменяется форма эллипса с изменением эксцентриситета гиперболы. 13. Дайте определение гиперболы. Напишите каноническое уравнение гиперболы. 14. Напишите формулу для определения эксцентриситета гиперболы. Напишите уравнения для нахождения асимптот гиперболы. 15. Сформулируйте определение параболы. Напишите каноническое уравнение параболы, симметричной относительно оси Оу. 2.2. Векторная алгебра и аналитическая геометрия в пространствеГл. XVIII [1]; № 372, 382, 397, 405, 418, 421 [3]. Гл. XIX § 1 – 4 [1]; № 452, 455, 457, 496 [3]. Разберите решение задачи 4 данного пособия. Задача 4. Даны координаты трех точек: А(3; 0; −5), В (6; 2; 1), С (12; −12; 3). Требуется: 1) Записать векторы 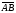 и и 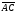 в системе орт и найти модули этих векторов. в системе орт и найти модули этих векторов.2) Найти угол между векторами 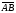 и и 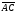 ; 3) составить уравнение плоскости, проходящей через точкуС перпендикулярно вектору ; 3) составить уравнение плоскости, проходящей через точкуС перпендикулярно вектору 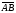 . .Решение. 1. Если даны точки М1(х1; у1; z1) bV2 (х2; у2; z2), то вектор 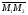 через орты через орты 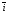 , , 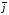 , , 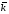 выражается следующим образом: выражается следующим образом: 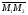 = (х2– х1) = (х2– х1) 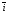 +(у2– у1) +(у2– у1) 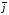 +(z2 – z1) +(z2 – z1)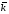 = aх = aх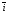 +ах +ах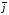 +ах +ах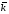 (7) (7)Подставляя в эту формулу координаты точекА и В, имеем: 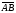 =(6–3) =(6–3)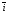 +(2–0) +(2–0) 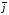 +(1+5) +(1+5)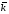 =3 =3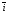 +2 +2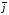 +6 +6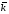 Подобным образом 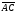 = =(12–3) = =(12–3) 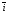 +(−12–0) +(−12–0) 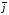 +(3+5) +(3+5) 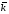 =9 =9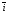 −12 −12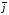 +8 +8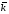 Модуль вектора 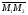 вычисляется по формуле вычисляется по формуле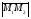 = =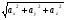 (8) (8)Подставляя в формулу (8) найденные раннее координаты векторов 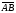 и и 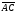 , находим их модули: , находим их модули: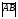 = =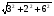 =7, =7, 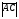 = =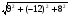 = 17. = 17.2. Косинус угла α, образованного векторами 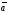 · ·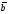 , равен их скалярному произведению, деленному на произведение их модулей , равен их скалярному произведению, деленному на произведение их модулей cos α = 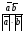 (9) (9)Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат, то 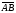 · ·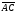 =3·9+2·(−12)+6·8=51.Применяя (9), имеем: =3·9+2·(−12)+6·8=51.Применяя (9), имеем:сos α = =cos 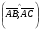 = = 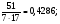 α ≈ 64º37'. α ≈ 64º37'.3. Известно, что уравнение искомая плоскость проходит через точку М0(х0;у0;z0) перпендикулярно вектору n 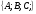 , имеет вид , имеет видА( х–х0)+В(у–у0)+С(z–z0)=0. (10) По условию задачи искомая плоскость проходит через точкуС (12;−12;3) перпендикулярно вектору 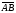 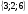 . Подставляя в (4) А=3, В=2, С=6, х0=12, у0=−12, z0=3, получим:3(х−12)+2(у+12)+6(z–3)=0,3х+2у+6z−30=0 – искомое уравнение плоскости. . Подставляя в (4) А=3, В=2, С=6, х0=12, у0=−12, z0=3, получим:3(х−12)+2(у+12)+6(z–3)=0,3х+2у+6z−30=0 – искомое уравнение плоскости.2.2.1. Вопросы для самопроверки
2.3. Элементы линейной алгебрыГл. XXI[5]; № 592, 624, 628 [3]. Разберите решение задачи 5 данного пособия. Задача 5. Данную систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы: 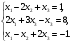 Решение. Обозначим через А–матрицу коэффициентов при неизвестных; Х–матрицу-столбец неизвестных Х1, Х2, Х3; Н – матрицу-столбец свободных членов: А= 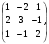 Х= Х=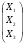 , Н= , Н=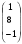 , ,С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А·Х=Н(11) Если матрица А – невырожденная (ее определитель ∆ отличен от нуля), то она имеет обратную матрицу А-1, получим:А-1·А·Х=А-1·Н. Но А-1·А=Е(Е – единичная матрица), а ЕХ = Х, поэтому Х=А-1·Н. (12) Равенство (12) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1. Пусть имеем невырожденную матрицу А= 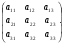 Тогда А-1= Тогда А-1=  , (13) , (13)где Аij (i=1, 2, 3; j=1, 2, 3) – алгебраическое дополнение элемента аij в определителе матрицы А, которое является произведением (−1)i+jна минор (определитель) второго порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А. Вычислим определитель ∆ и алгебраические дополнения Аijэлементов матрицы А. ∆=  = 10 = 10 0 0 следовательно матрицы А имеет обратную матрицу А-1. А11=(−1)i+1. 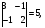 A12 =(−1)1+2. A12 =(−1)1+2.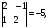 A13=(−1)1+3. 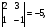 A21=(−1)2+1. A21=(−1)2+1.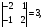 A22=(−1)2+2. 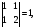 A23=(−1)2+3. A23=(−1)2+3.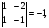 A31=(−1)3+1. 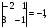 A32=(−1)3+2. A32=(−1)3+2.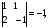 A33=(−1)3+3. 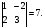 Тогда А-1 = 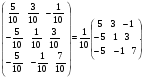 По формуле (12) находим решение данной системы уравнений в матричной форме: Х=А-1·Н= 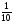 · · 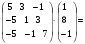  = =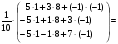 = 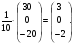 Отсюда х1=3, х2=0, х3=−2. 2.3.1. Вопросы для самопроверки1. Что называется определителем второго, третьего, n-го порядков? 2. Назовите основные свойства определителей. 3. Что называется минором, алгебраическим дополнением элемента определителя? 4. Напишите формулу Крамера решения системы линейных уравнений. В каких случаях их можно использовать? 5. Назовите схему решения системы линейных уравнений по методу Гаусса. 6. Что называется матрицей? 7. Как определяются основные действия над матрицами? 8. Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной? 9. Что называется рангом матрицы? Как найти ранг матрицы? 10. Сформулируйте теорему Кронекера-Капелли. 11. Опишите матричный способ решения системы линейных уравнений. 12. Какова геометрическая интерпретация систем линейных уравнений и неравенств? 2.4. Введение в анализГл. VI §1 – 9[2]; № 683, 685, 700, 701[3]. Гл. VII § 1 – 13[2]; № 716, 734, 736, 738, 744, 747, 782, 789[3]. Гл. VIII [2]; № 816, 820, 825 (2, 3) [3]. Разберите решение задач 6, 7, данного пособия. Задача 6. Вычислить пределы: а) 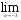 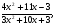 б) б) 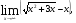 в) 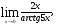 г) г) 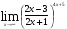 Решение: а) подстановка предельного значения аргумента х=−3 приводит к неопределенному выражению вида 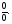 Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при х Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при х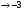 : :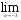 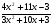 = =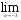 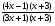 = =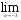 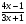 = =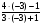 = =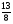 ; ;б) при 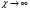 выражение выражение 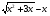 дает неопределенность вида дает неопределенность вида 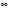 − −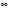 . Для ее устранения умножим и разделим это выражение на ( . Для ее устранения умножим и разделим это выражение на (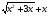 ): ):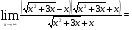 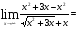 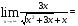 = 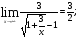 в) обозначим 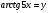 . Тогда . Тогда 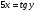 и и 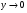 при при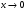 . Применяя свойства пределов и формулу первого замечательного предела . Применяя свойства пределов и формулу первого замечательного предела 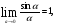 имеем: имеем: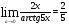 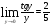 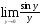 · ·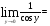 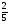 ·1·1= ·1·1= 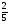 ; ;г) при 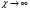 выражение выражение 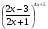 является неопределенностью вида 1∞. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при является неопределенностью вида 1∞. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при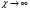 величины и применим формулу второго замечательного предела: величины и применим формулу второго замечательного предела: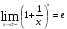 .Тогда имеем: .Тогда имеем: 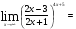 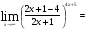 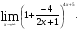 Пусть 2х+1= −4у. Тогда 4х+5=−8у+3 и у 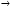 − −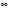 при при 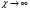 . Переходя к переменной у, получим: . Переходя к переменной у, получим: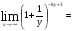 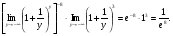 Задача 7. Исследовать на непрерывность функцию у = 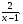 Решение. Данная функция является элементарной. Известно, что всякая элементарная функция непрерывна на своей области определения. Данная функция определена на интервалах (−∞; 1) и (1; ∞) и, следовательно, она непрерывна на этих интервалах. В точке х=1 функция имеет разрыв второго рода, поскольку в этой точке отсутствуют конечные односторонние пределы. График функции дан на рис. 2.4. 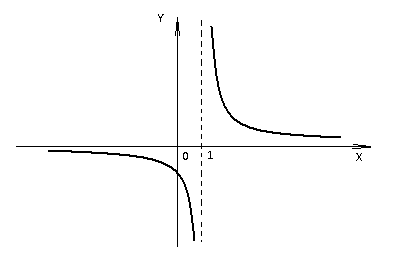 Рис. 2.4. Решение задачи 7 2.4.1. Вопросы для самопроверки1. Сформулируйте определение понятия функции. 2. Что называется областью определения функции? Областью изменения функции? 3. Перечислите основные элементарные функции. Назовите их основные свойства. 4. Какие функции называются элементарными? Приведите примеры. 5. Что называется пределом числовой последовательности? 6. Сформулируйте определение предела функции. 7. Назовите основные свойства пределов функций. 8. Какая функция называется бесконечно малой? бесконечно большой? 9. Назовите свойства бесконечно малых функций. 10. Напишите формулы первого и второго замечательных пределов. 11. Какие логарифмы называются натуральными? 12. Дайте определение односторонних пределов функции в точке. 13. Какая функция называется непрерывной в точке? На интервале? 14. Какая точка называется точкой разрыва первого рода? второго рода? 15. Перечислите основные свойства непрерывных на отрезке функций. 2.5. Производная и дифференциалГл. IX [2], № 907, 908, 910 [3]. Гл. X [2]; № 850, 857, 875, 888, 945, 956 [3]. Гл. XII [2]; № 1067, 1075, 1077 [3]. Разберите решение задачи 8 данного пособия. Задача 8. Найдите производные функции: а) у=ln 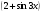 ; ; б) у= 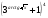 ; ;в) 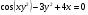 . .Решение: а) последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем: у' = 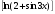 ' = ' = 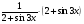 '= '== 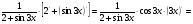 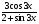 ; ;б) у'= 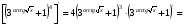 =4 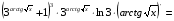 =4 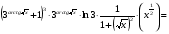 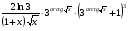 ; ;в) в данном случае функциональная зависимость задана в неявном виде. Для нахождения производной у' нужно продифференцировать по переменной х обе части уравнения, считая при этом уфункцией от х, а затем полученное уравнение разрешить относительно у': −sin 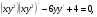 −sin −sin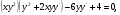 −y 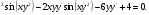 Из последнего уравнения находим у': 2 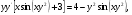 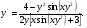 2.5.1. Вопросы для самопроверки1. Что называется производной функции? 2. Каков геометрический, физический смысл производной? 3. Как взаимосвязаны непрерывность функции и ее дифференцируемость в точке? 4. Напишите основные правила дифференцирования функций. 5. Напишите формулы дифференцирования основных элементарных функций. 6. Сформулируйте правило дифференцирования сложной функции. 7. Что называется дифференциалом функции? 8. Каков геометрический смысл дифференциала функции. 9. Перечислите основные свойства дифференциала функции. 10. Напишите формулу, позволяющую находить приближенное значение функции при помощи ее дифференциала. 11. Как найти производную второго, третьего, n-го порядков? 12. Как найти дифференциал второго порядка от данной функции? 2.6. Приложения производнойГл. XI, § 1-3, 7-10 [2]; № 1162, 1167, 1201, 1222, 1229 [3]. Разберите решение задач 9, 10 данного пособия. Задача 9. Исследовать функцию у= 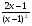 и построить ее график. и построить ее график.Решение. Исследование функции проведем по следующей схеме: 1. Найдем область определения функции. 2. Исследуем функцию на непрерывность. 3. Установим, является ли данная функция четной, нечетной. 4. Найдем интервалы возрастания и убывания функции и точки экстремума. 5. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. 6. Найдем асимптоты кривой. Реализуем указанную схему: 1. Функция определена при всех значениях аргумента х, кроме х = 1. 2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах (−∞; 1) и (1; ∞). 3. Для установления четности или нечетности функции проверим выполнимость равенств 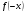 = =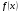 (тогда f(х) – четная функция) или (тогда f(х) – четная функция) или 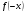 = = 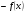 (для нечетной функции) для любых х и −х из области определения функции: (для нечетной функции) для любых х и −х из области определения функции: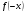 = =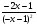 , , 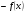 =− =− 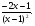 Следовательно, 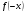  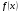 и и 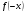  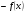 , то есть данная функция не является ни четной, ни нечетной. , то есть данная функция не является ни четной, ни нечетной.4. Для исследования функции на экстремум найдем ее первую производную: у'= 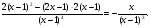 у'=0 при 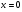 и у' − не существует при и у' − не существует при 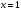 . Тем самым имеем две критические точки: . Тем самым имеем две критические точки: 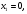 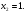 Но точка Но точка 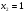 не принадлежит области определения функции, экстремума в ней быть не может.Разобьем числовую ось на три интервала (рис. 5): (−∞; 0), (0; 1), (1; ∞).В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительная и данная функция возрастает. При переходе через точку не принадлежит области определения функции, экстремума в ней быть не может.Разобьем числовую ось на три интервала (рис. 5): (−∞; 0), (0; 1), (1; ∞).В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительная и данная функция возрастает. При переходе через точку 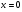 первая производная меняет свой знак с минуса на плюс, поэтому в этой точку функция имеет минимум: уmin=y(0)=−1. Значит, А(0; −1) − точка минимума.На рис. 2.5 знаками +, −указаны интервалы знакопостоянства производной у', а стрелами – возрастание и убывание исследуемой функции. первая производная меняет свой знак с минуса на плюс, поэтому в этой точку функция имеет минимум: уmin=y(0)=−1. Значит, А(0; −1) − точка минимума.На рис. 2.5 знаками +, −указаны интервалы знакопостоянства производной у', а стрелами – возрастание и убывание исследуемой функции.+ – max min – Рис. 2.5. Решение задачи 9 5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную: у''=− 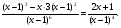 у''=0 при 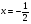 и у''− не существует при и у''− не существует при 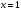 . Разобьем числовую ось на три интеграла (рис. 2.6); (−∞; − . Разобьем числовую ось на три интеграла (рис. 2.6); (−∞; −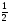 ), (− ), (−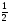 ; 1), (1; ∞). На первом интервале вторая производная у''=0 при ; 1), (1; ∞). На первом интервале вторая производная у''=0 при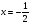 − абсцисса точки перегиба.Следовательно, В − абсцисса точки перегиба.Следовательно, В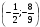 - точка перегиба графика функции. - точка перегиба графика функции._ разрыв перегиб + + X 1 Рис. 2.6. Решение задачи 9 6. 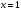 − точка разрыва функции, причем − точка разрыва функции, причем 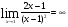 .Поэтому прямая .Поэтому прямая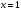 является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты 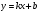 воспользуемся формулами: воспользуемся формулами: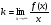 , , 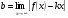 . .Тогда 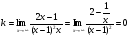 , ,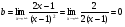 . .Значит прямая у=0 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 2. 7. 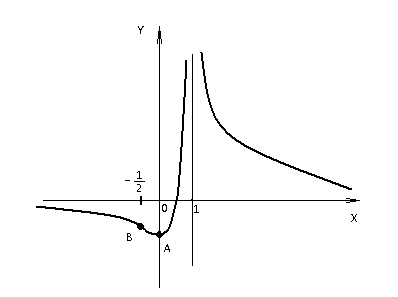 Рис. 2.7. Решение задачи 9 Задача 10. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л воды, чтобы затраты на его лужение были наименьшими? Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной.Обозначим через  дм − сторону основания, дм − сторону основания, 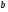 дм− высоту резервуара. Тогда площадь S его поверхности равна дм− высоту резервуара. Тогда площадь S его поверхности равна 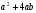 , а объем V= , а объем V=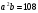 . Отсюда: . Отсюда: 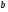 = =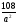 и S= и S=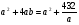 Полученное соотношение устанавливает зависимость между площадью поверхности резервуара S(функция) и стороной основания а (аргумент). Исследуем функцию Sна экстремум. Найдем первую производную S', приравняем ее к нулю и решим полученное уравнение: S'=2 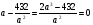 Отсюда 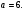 S' S'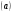 >0 при >0 при  >6, S' >6, S'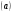 <0 при <0 при  <6. Следовательно, при <6. Следовательно, при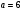 функция S имеет минимум. Если функция S имеет минимум. Если 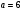 , то , то 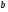 =3. Таким образом, затраты на лужение резервуара емкостью 108 л будут наименьшим, если он имеет размеры 6дмX6дмХ3дм. =3. Таким образом, затраты на лужение резервуара емкостью 108 л будут наименьшим, если он имеет размеры 6дмX6дмХ3дм.2.6.1. Вопросы для самопроверки1. Сформулируйте теоремы Роля, Лагранжа. Каков их геометрический смысл? 2. Какая функция называется возрастающей? убывающей? 3. Сформулируйте необходимый, достаточный признаки возрастания и убывания функции. 4. Какие точки называются стационарными? критическими? 5. Назовите достаточные признаки экстремума функции. 6. Какая кривая называется выпуклой? вогнутой? 7. Как найти интервалы выпуклости и вогнутости кривой? 8. Сформулируйте достаточный признак существования точки перегиба кривой. 9. Что называется асимптотой кривой? Как найти вертикальные и наклонные асимптоты? 10. Назовите схему исследования функции и построения ее графика. 11. В каком случае применяется правило Лопиталя при вычислении пределов? 2.7. Функции нескольких переменныхГл. XX[2]; № 1854, 1862, 1885, 1926, 2031, 2048 [3]. 2.7.1. Вопросы для самопроверки1.Дайте определение функции двух независимых переменных. Приведите примеры. 2. Что называется областью определения функции двух независимых переменных? Каково геометрическое изображение функции двух переменных? 3. Что называется частным и полным приращением функции двух независимых переменных? 4. Сформулируйте определение предела функции двух переменных. 5. Какая функция называется непрерывной в точке? в области? 6. Дайте определение частных производных первого порядка функции двух переменных. Каков их геометрический смысл? 7. Что называется полным дифференциалом функции двух переменных? 8. Как найти частные производные второго порядка функции двух переменных? 9. Что является необходимым условием экстремума функции двух переменных? 10. Сформулируйте достаточный признак экстремума функции двух переменных. 2.8. Неопределенный интегралГл. XIII[2]; № 1264, 1267, 1286, 1318, 1363, 1365, 1426, 1572 [3]. 2.8.1. Вопросы для самопроверки1. Сформулируйте определение первообразной функции. 2. Что называется неопределенным интегралом от данной функции? 3. Перечислите основные свойства неопределенного интеграла. 4. Напишите формулы таблицы основных интегралов. 5. В чем сущность метода интегрирования заменой переменной? 6. Напишите формулу интегрирования по частям в неопределенном интеграле. 2.9. Определенный интегралГл. XIV, XV [2]; № 1598, 1607, 1619, 1622, 1629, 1636, 1670, 1686 [3]. Разберите решение задачи 11 данного пособия. Задача 11. Вычислить площадь фигуры, ограниченной линиями у=х2+4х, у=х+4 (рис. 2.8). 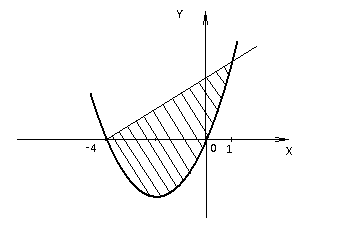 Рис. 2.8. Решение задачи 11 Решение. Площадь Sфигуры, ограниченной сверху и снизу непрерывными линиями у=f(х) и у= 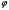 (х), пересекающими в точках абсциссами (х), пересекающими в точках абсциссами 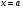 и и 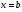 , определяется по формуле , определяется по формуле S= 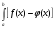 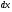 (14) (14)Для нахождения точек пересечения данных линий решаем систему уравнений 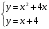 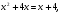 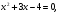 откуда откуда 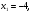 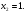 Применяя формулу (14), получим: 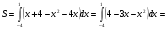 = 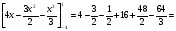 20 20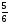 (кв. ед.). (кв. ед.). 2.9.1. Вопросы для самопроверки1. Назовите задачи, приводящие к понятию определенного интеграла. 2. Напишите интегральную сумму для функции у=f(х) на отрезке 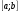 . .3. Что называется определенным интегралом от функции у=f(х) на 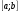 ? ?4. Каков геометрический смысл определенного интеграла? 5. Перечислите основные свойства определенного интеграла. 6. Чему равна производная от определенного интеграла с переменным верхним пределом интегрирования? 7. Напишите формулу Ньютона – Лейбница. 8. Напишите формулу интегрирования по частям в определенном интеграле. 9. Как вычислить объем тела, образованного вращением плоской фигуры вокруг осиОх? оси Оу? 10. Дайте определение несобственного интеграла с бесконечными пределами интегрирования. 11. Сформулируйте понятие несобственного интеграла от разрывной функции. |

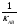 =−
=−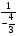 =
=