5. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 2
В задачах 181 – 200 найти общее решение дифференциальных уравнений первого порядка.
181. 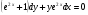 . 182. . 182. 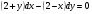 . .
183. 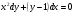 . 184. . 184. 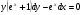 . .
185. 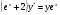 . 186. . 186. 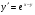 . .
187. 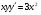 . 188. . 188. 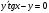 . .
189. 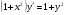 . 190 . 190 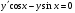 . .
191. 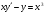 . 192. . 192. 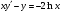 . .
193. 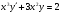 . 194. . 194. 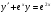 . .
195. 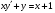 . 196. . 196. 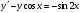 . .
197. 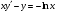 . 198. . 198. 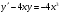 . .
199. 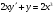 . 200. . 200. 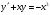 . .
В задачах 201 – 210 найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям .
201.  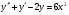 , , 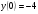 , , 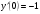 . .
202. 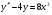 , , 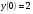 , , 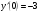 . .
203. 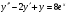 , , 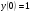 , , 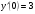 . .
204. 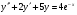 , , 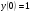 , , 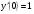 . .
205. 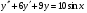 , , 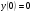 , , 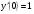 . .
206. 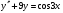 , , 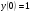 , , 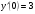 . .
207. 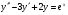 , , 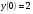 , , 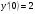 . .
208. 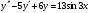 , , 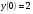 , , 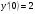 . .
209. 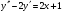 , , 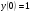 , , 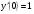 . .
210. 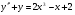 , , 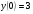 , , 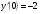 . .
В задачах 211 -230 дан степенной ряд 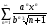 . .
При заданных значениях a и b написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
211. а = 2, b = 3. 212. a = 3, b = 5.
213. a = 4, b = 7 . 214. a = 5, b = 9.
215. a = 7, b = 6 . 216 a = 2, b = 5.
217. a = 3, b = 2. 218. a = 4, b = 3.
219. a = 5, b = 2. 220. a = 6, b = 4.
221. a = 3, b = 7. 222. a = 4, b = 5.
223. a = 8, b = 3. 224. a = 7, b = 4.
225. a = 5, b = 7. 226. a = 2, b = 6.
227. a = 3, b = 4. 228. a = 7, b = 5.
229. a = 5, b = 8. 230. a = 2, b = 4.
В задачах 231 – 250 вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
231. 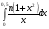 . 232. . 232. 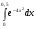 . .
233. 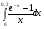 . 234. . 234. 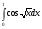 . .
235. 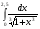 . 236. . 236. 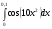 . .
237. 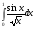 . 238. . 238. 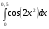 . .
239. 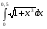 . 240. . 240. 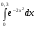 . .
241 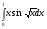 . 242. . 242. 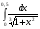 . .
243. 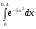 . 244. . 244. 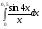 . .
245. 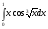 . 246. . 246. 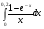 . .
247. 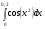 . 248. . 248. 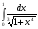 . .
249. 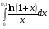 . 250. . 250. 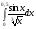 . .
В читальном зале имеется 6 учебников по теории вероятности, из которых 2 в мягком переплете. Библиотекарь взял два учебника. Найти вероятность того, что оба учебника окажутся в мягком переплете.
Студент знает ответы на 20 из25 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором три вопроса.
Для некоторой местности в июле шесть пасмурных дней. Найти вероятность того, что первого и второго июля будет ясная погода.
Из 200 рабочих норму выработки не выполняют 15 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму.
Три стрелка по мишени. Вероятность попадания в цель первым стрелком равна 0,6, вторым – 0,7, третьим – 0,8. Найти вероятность того, что при одном выстреле попадут в цель : а) все три стрелка; б) попадет хотя бы один из них.
В ящике лежат 20 электрических лампочек, из которых 2 нестандартные . Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными.
Одновременно бросаются две игральные кости. Найти вероятность того, что на каждой кости появится нечетное количество очков.
Из заготовленной для посева пшеницы зерно первого сорта составляет 40 %, второго сорта – 50 %, третьего сорта – 10 %. Вероятность того, что взойдет зерно первого сорта равна 0,8, второго – 0,5, третьего – 0,3. Найти вероятность того, что взойдут наугад взятое зерно.
В магазин поступили телевизоры из трех заводов. Вероятность того, что телевизор изготовлен на первом заводе, равна 0,3, на втором – 0,2, на третьем - 0,5. Вероятность того, что телевизор окажется бракованным, для первого завода равна 0,2, для второго – 0,1, для третьего – 0,3. Найти вероятность того, что наугад взятый телевизор окажется небракованным.
В мастерской на трех станках изготавливаются однотипные детали. Вероятность безотказной работы первого станка равна 0,8, второго – 0,7, третьего – 0,9. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,1. Найти вероятность того, что наугад выбранная деталь окажется стандартной.
Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти вероятность того, что цель будет поражена: а) три раза; б) не более двух раз.
Вероятность всхожести пшеницы равна 0,8. Какова вероятность того, что из 5 семян взойдут не менее 3?
Вероятность попадания в цель при одном выстреле равна 0,8. Написать закон распределения вероятностей попаданий в цель при 5 выстрелах и построить многоугольник распределения вероятностей.
Всхожесть семян пшеницы составляет 90 %. Определить наиболее вероятное число всходов из 200 посеянных семян.
Семена пшеницы содержат 0,2% сорняков. Найти вероятность того, что в 1000 семян будет 6 семян сорняков.
В задачах 266 – 270 дана вероятность p того, что семя злака прорастет. Найти вероятность того, что из n посеянных семян прорастет ровно R семян.
266. n = 100, p = 0,9, R = 95.
267. n = 400, p = 0,8, R = 330.
268. n = 900, p = 0,36, R = 340.
269. n = 225, p = 0,64, R = 158.
270. n = 250, p = 0,81, R = 200.
В задачах 271-280 дана вероятность р появления события А в каждом из n независимых испытаний. Найти вероятность того, что в этих испытаниях событие А появится не менее  раз и не более раз и не более  раз. раз.
271. n=360, p=0,8,  =280, =280,  =300. =300.
272. n=490, p=0,6,  =320, =320,  =350. =350.
273. n=640, p=0,9,  =500, =500,  =540. =540.
274. n=225, p=0,2,  =50, =50,  =60. =60.
275. n=810, p=0,4,  =340, =340,  =400. =400.
276. n=250, p=0,7,  =150, =150,  =180. =180.
277. n=300, p=0,3,  =110, =110,  =130. =130.
278. n=625, p=0,8,  =480, =480,  =500. =500.
279. n=100, p=0,5,  =60, =60,  =80. =80.
280. n=256, p=0,9,  =200, =200,  =220. =220.
В задачах 281 – 290 задан закон распределения дискретной случайной величины Х ( в первой строке указаны возможные значения величины Х, во второй строке даны вероятности p этих значений ). Найти: 1) математическое ожидание M (X); 2) дисперсию D (X); 3) среднее квадратическое отклонение σ.
281. X 8 4 6 5
p 0,1 0,3 0,2 0,4
282. X 23 25 27 29
p 0,2 0,1 0,3 0,4
283. X 10 8 6 9
p 0,4 0,1 0,3 0,2
284. X 32 40 37 35
p 0,1 0,3 0,4 0,2
285. X 42 41 43 45
p 0,3 0,3 0,2 0,2
286. X 15 11 13 12
p 0,2 0,5 0,2 0,1
287. X 52 54 57 51
p 0,1 0,4 0,3 0,2
288. X 21 20 22 26
p 0,5 0,2 0,2 0,1
289. X 34 30 32 36
p 0,2 0,4 0,3 0,1
290. X 50 48 51 53
p 0,3 0,2 0,2 0,3
В задачах 291 – 300 случайная величина Х задана интегральной функцией распределения F (x). Найти: 1) дифференциальную функцию распределения f (x); 2) математическое ожидание M (X); 3) дисперсию D(X).
291. 0 при х < 0,
F (x) = x ² при 0 ≤ х ≤ 1,
1 при х > 1.
292. 0 при х<0,
F (x) = 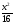 при 0≤х≤4, при 0≤х≤4,
1 при х>4.
293. 0 при х<2,
F (x) = х-2 при 2 ≤ х ≤ 3,
1 при х>3.
294. 0 при х<0,
F (x) = 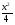 при 0 ≤ х ≤ 2, при 0 ≤ х ≤ 2,
1 при х>2.
295. 0 при х>4,
F (x) = х – 4 при 4 ≤ х ≤ 5,
при х>5.
296. 0 при х<0,
F (x) = 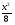 при 0 ≤ х ≤ 2, при 0 ≤ х ≤ 2,
1 при х > 2.
297. 0 при х < 0,
F (x) = 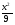 при 0 ≤ х ≤ 3, при 0 ≤ х ≤ 3,
1 при х > 3.
299. 0 при х < 0,
F (x) = х при 0 ≤ х ≤ 1,
1 при х > 1.
300. 0 при х < 0,
F (x) = 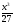 при 0 ≤ х ≤ 3, при 0 ≤ х ≤ 3,
1 при х > 3.
Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм . Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Найти процент стандартных деталей.
Средний диаметр стволов деревьев на некотором участке равен 25 см, среднее квадратическое отклонение равно 5 см. считая диаметр ствола случайной величины, распределенной нормально, найти процент деревьев, имеющих диаметр свыше 20 см.
Процент всхожести семян равен 90%. Оценить вероятность того, что из 1000 посеянных семян взойдут от 850 до 950 семян включительно.
Среднее квадратическое отклонение нормально распределенной случайной величины равно 0,5. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 1.
Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 150 мм и средним квадратическим отклонением 0,5 мм. Какую точность размера детали можно гарантировать с вероятностью 0,95.
Средний вес зерна равен 0,2 г, среднее квадратическое отклонение равно 0,05 г. Определить вероятность того, что вес наудачу взятого зерна окажется в пределах от 0,16 г до 0,22 г.
норма высева семян на 1 га равна 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим 10 кг. Определить количество семян, обеспечивающих посев на площадь 100 га с гарантией 0,95.
Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилось и характеризуется средним квадратическим отклонением 0,4 мм. На сколько повысился процент бракованных деталей?
Масса яблок, средняя величина которой равна 150 г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20 г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130 г до 180 г.
Устройство состоит из 20 однотипных независимо работающих элементов. Вероятность безотказной работы каждого элемента за 10 часов 0,9. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом отказов за 10 часов окажется меньше двух.
Задачи 311 – 320. Хозяйство имеет возможность приобрести не более  трехтонных автомашин и не более трехтонных автомашин и не более 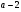 пятитонных автомашин. Отпускная цена трехтонного грузовика – 4 000 у.е., а пятитонного – 5 000 у.е. Хозяйство может выделить для приобретения автомашин пятитонных автомашин. Отпускная цена трехтонного грузовика – 4 000 у.е., а пятитонного – 5 000 у.е. Хозяйство может выделить для приобретения автомашин 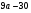 тыс. у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной? Задачу решить графическим методом. Значения параметра тыс. у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной? Задачу решить графическим методом. Значения параметра  даны в табл. 3: даны в табл. 3:
Таблица 3
Номер задания
|
311
|
312
|
313
|
314
|
315
|
316
|
317
|
318
|
319
|
320
|
Значение 
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
|
 Скачать 1.04 Mb.
Скачать 1.04 Mb.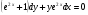 . 182.
. 182. 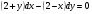 .
.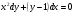 . 184.
. 184. 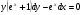 .
.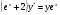 . 186.
. 186. 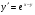 .
.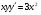 . 188.
. 188. 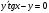 .
.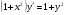 . 190
. 190 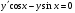 .
.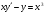 . 192.
. 192. 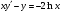 .
.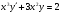 . 194.
. 194. 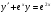 .
.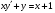 . 196.
. 196. 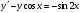 .
.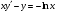 . 198.
. 198. 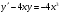 .
.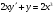 . 200.
. 200. 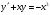 .
.
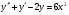 ,
, 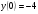 ,
, 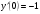 .
. 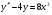 ,
, 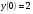 ,
, 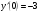 .
.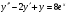 ,
, 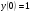 ,
, 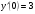 .
.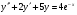 ,
, 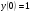 ,
, 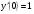 .
.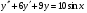 ,
, 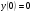 ,
, 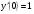 .
.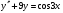 ,
, 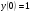 ,
, 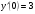 .
.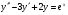 ,
, 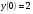 ,
, 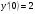 .
.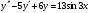 ,
, 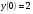 ,
, 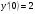 .
.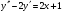 ,
, 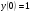 ,
, 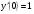 .
.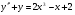 ,
, 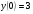 ,
, 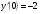 .
.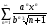 .
.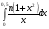 . 232.
. 232. 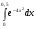 .
.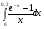 . 234.
. 234. 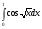 .
.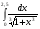 . 236.
. 236. 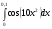 .
.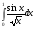 . 238.
. 238. 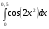 .
.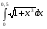 . 240.
. 240. 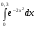 .
.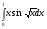 . 242.
. 242. 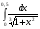 .
.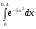 . 244.
. 244. 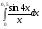 .
.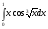 . 246.
. 246. 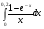 .
.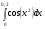 . 248.
. 248. 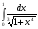 .
.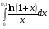 . 250.
. 250. 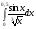 .
. раз и не более
раз и не более  раз.
раз. =280,
=280,  =300.
=300. =320,
=320,  =350.
=350. =500,
=500,  =540.
=540. =50,
=50,  =60.
=60. =340,
=340,  =400.
=400. =150,
=150,  =180.
=180. =110,
=110,  =130.
=130. =480,
=480,  =500.
=500. =60,
=60,  =80.
=80. =200,
=200,  =220.
=220. 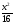 при 0≤х≤4,
при 0≤х≤4,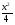 при 0 ≤ х ≤ 2,
при 0 ≤ х ≤ 2,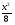 при 0 ≤ х ≤ 2,
при 0 ≤ х ≤ 2,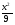 при 0 ≤ х ≤ 3,
при 0 ≤ х ≤ 3,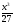 при 0 ≤ х ≤ 3,
при 0 ≤ х ≤ 3, трехтонных автомашин и не более
трехтонных автомашин и не более 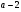 пятитонных автомашин. Отпускная цена трехтонного грузовика – 4 000 у.е., а пятитонного – 5 000 у.е. Хозяйство может выделить для приобретения автомашин
пятитонных автомашин. Отпускная цена трехтонного грузовика – 4 000 у.е., а пятитонного – 5 000 у.е. Хозяйство может выделить для приобретения автомашин 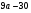 тыс. у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной? Задачу решить графическим методом. Значения параметра
тыс. у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной? Задачу решить графическим методом. Значения параметра  даны в табл. 3:
даны в табл. 3: