_КР Математика 38.05.02 2016. Учебнометодические указания по выполнению контрольной работы Дисциплина математика
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
3. УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ № 23.1. Дифференциальные уравненияГл. XXII § 1-13 [2]; № 2058, 2067, 2094, 2102, 2165, 2186, 2213, 2215 [3]. Разберите решение задач 12, 13 данного пособия. Задача12.Решить уравнение у'−уtgx=−y2cosx. Решение. Данное уравнение является уравнением Бернулли. Для его решения (как и для линейного уравнения) искомую функцию у представим в виде произведения двух других функций: u=u(x) и υ=υ(х), то есть введем подстановку у= u·υ. Тогда у'=u'υ+uυ' и данное уравнение примет вид: u'υ+uυ'− uυ tgx=− u2υ2cosx или υ(u'−utgx)+ uυ'=− u2υ2cosx (15) Выберем функцию u так, чтобы u'− utgx=0 (16) При подобном выборе функции u уравнение (1) примет вид uυ'==− u2υ2cosxили υ'=− uυ2cosx (17) Решая (16) как уравнение с разделяющими переменными, имеем: 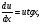 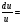 tg x d x, ln u=−ln cos x, u= tg x d x, ln u=−ln cos x, u=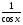 . .Здесь производная постоянная С = 0. Подставляя найденное значение u в уравнение (17), имеем: 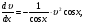 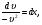 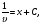 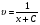 .Тогда у= u·υ= .Тогда у= u·υ=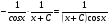 − общее решение данного уравнения. − общее решение данного уравнения.Задача 13. Найти частное решение уравнения у''+4у=4sin2x-8cos2x, удовлетворяющее начальным условиям у(0)=0, у'(0)=0. Решение. Общее решение у данного уравнения равно сумме общего решения уодн однородного уравнения и какого-либо частного решения 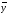 данного уравнения, то есть у = уодн+ данного уравнения, то есть у = уодн+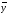 . Для нахождения уоднсоставим характеристическое уравнение . Для нахождения уоднсоставим характеристическое уравнение 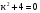 , имеющее комплексные корни , имеющее комплексные корни 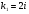 и и 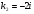 . В этом случае общее решение однородного уравнения ищем в виде: . В этом случае общее решение однородного уравнения ищем в виде:уодн= 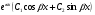 , (18) , (18)где 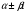 − комплексные корни характеристического уравнения. Подставив в (4) − комплексные корни характеристического уравнения. Подставив в (4) 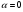 , , 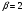 , имеем:уодн= , имеем:уодн=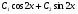 . Для нахождения частного решения . Для нахождения частного решения 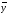 неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция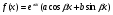 и числа и числа 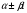 не являются корнями характеристического уравнения, то существует частное решение не являются корнями характеристического уравнения, то существует частное решение 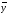 = =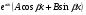 . Если же числа . Если же числа 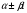 являются корнями характеристического уравнения, то существует частное решение: являются корнями характеристического уравнения, то существует частное решение: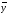 = =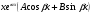 . .Применяя эту теорему при 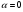 , ,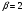 , имеем: , имеем: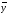 =x(Acos2x+Bsin2x) =x(Acos2x+Bsin2x)Дважды дифференцируя последнее равенство, находим у'':у''=(4В−4Ах)cos2x+(−4А−4Вх)sin2x.Подставив в данное уравнение 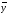 и у'', получим: и у'', получим:4В cos2x−4А sin2x=4 sin2x−8 cos2x,откудаА=−1, В=−2. Следовательно, 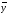 =−х(cos2x+2sin2x) иу= =−х(cos2x+2sin2x) иу=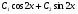 −х(cos2x+2sin2x). −х(cos2x+2sin2x).Найдем у':у'=−2С1sin2x+2С2cos2x- cos2x-2sin2x-х(−2sin2x+4 cos2x).Используя начальные условия, получим систему 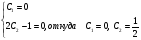 Следовательно, у= 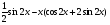 есть искомое частное решение данного дифференциального уравнения. есть искомое частное решение данного дифференциального уравнения.3.1.1. Вопросы для самопроверки1. Что называется дифференциальным уравнением? 2. Что называется общим решением дифференциального уравнения? частным решением? 3. Каков геометрический смысл частного решения дифференциального уравнения первого порядка? 4. Приведите примеры дифференциальных уравнений с разделяющимися переменными. 5. Какое дифференциальное уравнение первого порядка называется линейным? уравнением Бернулли? Укажите способ их решения. 6. Какое уравнение называется линейным дифференциальным уравнением второго порядка? 7. Какое уравнение называется характеристическим для однородного дифференциального уравнения второго порядка? 8. Какой вид имеет общее решение однородного дифференциального уравнения второго порядка в зависимости от дискриминанта характеристического уравнения? 9. Как найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его правая часть есть многочлен? показательная функция? тригонометрическая функция? 10. Какой вид имеет частное решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его правая часть есть многочлен? показательная функция? тригонометрическая функция? 3.2. РядыГл. XXI § 1-14[2]; № 2424, 2426, 2474, 2475, 2503, 2519, 2533[3]. Разберите решение задач 14, 15 данного пособия. Задача 14.Написать первыетри члена ряда 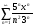 , найти интервал сходимости ряда и исследовать его сходимость на концах интервала. , найти интервал сходимости ряда и исследовать его сходимость на концах интервала. Решение. Беря последовательно n = 1, 2, 3, …, запишем данный ряд в виде: 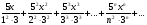 Для нахождения области сходимости ряда применим признак Даламбера: 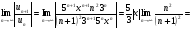 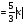 . .Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству 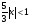 , или , или 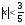 , или , или 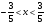 .Исследуем сходимость ряда на концах полученного интервала. При .Исследуем сходимость ряда на концах полученного интервала. При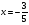 данный ряд принимает вид данный ряд принимает вид 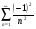 .Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при n→ ∞ . Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит, .Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при n→ ∞ . Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит, 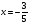 принадлежит области сходимости данного ряда.При принадлежит области сходимости данного ряда.При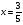 данный ряд принимает вид данный ряд принимает вид 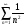 . Исследуем сходимостьКоши. Рассмотрим несобственный интеграл . Исследуем сходимостьКоши. Рассмотрим несобственный интеграл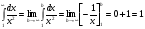 . .Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при x = 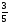 исходный ряд сходится. Таким образом, исходный ряд сходится. Таким образом, 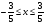 - область сходимости данного ряда. - область сходимости данного ряда.Задача 15. Вычислить 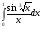 с точностью до 0,001. с точностью до 0,001.Решение. Представим подынтегральную функцию в виде степенного ряда. Заменив x в разложении функции sinxна 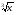 , имеем: , имеем: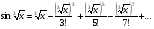 Тогда 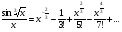 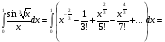 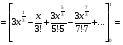 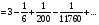 Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвертый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда 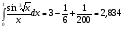 . .3.2.1. Вопросы для самопроверки
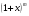 , ln (1+x) . , ln (1+x) .
3.3. Повторные независимые испытанияГл. 5[6]; № 112, 115, 119, 120, 131[7]. Разберите решения задач 16 – 19 методических указаний. Задача 16. Вероятность всхожести семян пшеницы равна 0,9.Какова вероятность того, что из четырех посеянных семян взойдут не менее трех? Решение. Пусть событиеА – из 4 семян взойдут не менее 3 семян; событие В – из 4 семян взойдут 3 семени; событие С – из 4семян взойдут 4 семени. По теореме сложения вероятностей P(A) = P(B) + P(C). Вероятности Р(В) и Р(С) определим по формуле Бернулли,применяемой в следующем случае. Пусть проводится серияn независимых испытаний, при каждом из которых вероятность наступления события постоянна и равна p, а вероятность не наступления этого события равна q =1 – p. Тогда вероятность того, что событиеА в n испытаниях появится ровно Rраз, вычисляется по формуле Бернулли 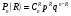 , (19) , (19)где 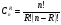 - число сочетаний из n элементов по R. - число сочетаний из n элементов по R.Тогда 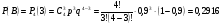 ; ;Искомая вероятность P(A) = 0,2916 + 0,6561 = 0,9477. Задача 17.Вероятность всхожести семян пшеницы равна 0,9. Найти вероятность того, что из 400 посеянных семян взойдут 350 семян. Решение. Вычислить искомую вероятность по формуле 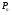 (350) (350)Бернулли затруднительно из-за громоздкости вычислений. Поэтому применим приближенную формулу, выражающую локальную теорему Лапласа: 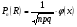 , (20) , (20)где 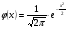 и и 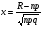 . .Из условия задачи p = 0,9; q = 1 – 0,9 = 0,1; n = 400; R = 350. Тогда 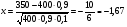 . .Из таблицы 1 приложений находим φ( - 1,67 ) = φ (1,67 ) = 0, 0989 . Искомая вероятность равна 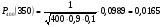 . .Задача 18.Среди семян пшеницы 0,02 % сорняков. Какова вероятность того, что при случайном отборе 10 000 семян будет обнаружено 6 семян сорняков? Решение. Применение Локальной теоремы Лапласа из-за малой вероятности p = 0, 0002 приводит к значительному отклонению вероятности от точного значения 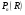 . Поэтому при малых значениях p для вычисления . Поэтому при малых значениях p для вычисления 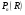 применяют асимптотическую формулу Пуассона применяют асимптотическую формулу Пуассона 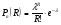 , где e=2,7182…, , где e=2,7182…, 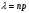 Эта формула используется при λ ≤ 10, причем, чем меньше p и больше n, тем результат точнее.По условию задачи p=0,0002; n=10 000; R=6.Тогда λ = 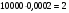 и и 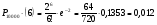 . .Задача 19.Процент всхожести семян пшеницы равен 90 %. Найти вероятность того, что из 500 посеянных семян взойдут от 400 до 440 семян . Решение. Если вероятность наступления события А в каждом из n испытаний постоянна и равна p, то вероятность 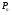 ( ( ≤ R ≤ ≤ R ≤  ) того, что событие А в таких испытаниях наступит не менее ) того, что событие А в таких испытаниях наступит не менее  раз и не более раз и не более  раз определяется по интегральной теореме Лапласа следующей формулой: раз определяется по интегральной теореме Лапласа следующей формулой: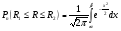 , (21) , (21)где 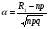 , , 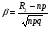 . .Функция 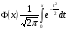 называется функцией Лапласа.В приложениях ( табл. 2 ) даны значения этой функции для 0 ≤ x ≤5. При x › 5 функция Ф (x) = 0,5. При отрицательных значениях x в силу нечетности функции Лапласа Ф (- х) = Ф (х). Используя функцию Лапласа, имеем: называется функцией Лапласа.В приложениях ( табл. 2 ) даны значения этой функции для 0 ≤ x ≤5. При x › 5 функция Ф (x) = 0,5. При отрицательных значениях x в силу нечетности функции Лапласа Ф (- х) = Ф (х). Используя функцию Лапласа, имеем: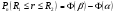 . По условию задачи n = 500; p = 0,9; q = 0,1; . По условию задачи n = 500; p = 0,9; q = 0,1;  = 400; = 400;  = 440. По приведенным выше формулам находим α иβ : = 440. По приведенным выше формулам находим α иβ :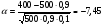 ; ; 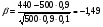 . .Тогда 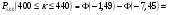 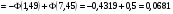 . .3.3.1. Вопросы для самопроверки
3.4. Случайные величины и их числовыехарактеристикиГл. 6, § 1 – 3, гл. 7, 8, 10, 11 [6]; № 165, 176, 188, 210, 254, 263, 276, 328,341[7]. Задача 20.Задан закон распределения дискретной случайной величины Х: Х 40 42 41 44, Р 0,1 0,3 0,2 0,4. Найти: 1) математическое ожидание М (Х). 2) Дисперсию D (Х). 3) Среднее квадратическое отклонение σ. Решение.1) Если закон распределения дискретной случайной величины задан таблицей Х 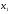 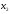 … … 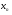 Р 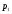 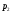 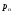 , ,где в первой строке даны значения случайной величины Х, а во второй – вероятности этих значений, то математическое ожидание М (Х) вычисляется по формуле 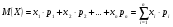 . .Тогда M (X)= 40 · 0,1 + 42 · 0,3 + 41 · 0,4 = 42,4. 2) Дисперсией D(X) дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е. 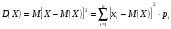 . .Эта величина характеризует среднее ожидаемое значение квадрата отклонения X от M (X). Из последней формулы имеем D (X) = ( 40 – 42,4 )²∙0,1+(42 – 42,4)2∙0,3+(41 – 42,4)2∙0,2+(44 – – 42,4)2∙0,4=2,42∙0,1+0,42∙0,3+1,420,2+1,62∙0,4=2,04. Дисперсия D(X) можно найти другим способом, исходя из следующего ее свойства: дисперсия D(X) равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания M (X), то есть D (X) = M (X²) - [ M (X) ]².Для вычисления M (X²) составим следующий закон распределения величины X² : X² 40² 42² 41² 44² P 0,1 0,3 0,2 0,4. Тогда M (X²) = 40² · 0,1 + 42² · 0,3 + 41² · 0,2 + 44² · 0,4 =160 + 529,2 + +336,2 + 774,4 = 1799,8 иD (X) = 1799,8 – 42,4² = 2,04. 3) Для характеристики рассеяния возможных значений случайной величины вокруг его среднего значения вводится среднее квадратическое отклонение σ (X) случайной величины X, равное квадратному корню из дисперсии D (X), то есть 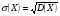 .Из этой формулы имеем: .Из этой формулы имеем: 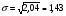 . .Задача 21.Непрерывная случайная величина Х задана интегральной функцией распределения 0 при х < 0, F (x) = х³ при 0 ≤ х ≤1, 1 при х > 1. Найти: 1) Дифференциальную функцию распределения f (x). 2) Математическое ожидание M (X); 3) дисперсию D (X) . Решение. 1) Дифференциальная функцией распределения f(x) непрерывной случайной величины X называется производная от интегральной функции распределения F (x) , то есть 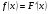 .Искомая дифференциальная функция имеет следующий вид: .Искомая дифференциальная функция имеет следующий вид:0 при х < 0 , f (x) = 3 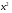 при 0 ≤ х ≤ 1, при 0 ≤ х ≤ 1,0 при х > 1. 2) Если непрерывная случайная величина Х задана функцией f (x) , то ее математическое ожидание определяется формулой 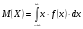 . .Так как функция f (x) при x< 0 и при x>1 равна нулю, то из последней формулы имеем 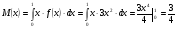 . .3) Дисперсию D (X) определим по формуле 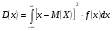 . .Тогда 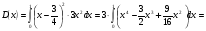 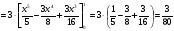 . .Задача 22. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40мм и средним квадратическим отклонением 3мм.Найти:1) вероятность того, что длина детали отклонится от ее математического ожидания не более чем 1,5мм. Решение: 1) Пусть Х - длина детали. Если случайная величина Х задана дифференциальной функцией f (х), то вероятность того, что Х примет значения, принадлежащие отрезку [α ; β ] , определяется по формуле 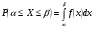 . .Вероятность выполнения строгих неравенств L 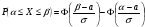 , (22) , (22)где Ф (х ) – функция Лапласа; a =M (X); σ = 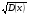 . .В задачеа = 40, α = 34, β = 43, σ = 3. Тогда 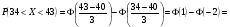 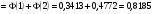 . .2) По условию задачи а – δ < Х < а + δ, где а = 40; δ = 1,5. Подставив в (1) α = а – δ, β = а + δ, имеем 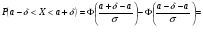 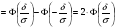 , , то есть 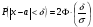 (23) (23)Из формулы (23) имеем: 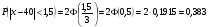 . .3.4.1. Вопросы для самопроверки
3.5. Элементы линейного программированияГл. XXVI § 3[2]. Задача 23.Предприятие имеет возможность приобрести не более 20 трехтонных и не более 18 пятитонных автомашин. Отпускная цена трехтонного грузовика 4000 у.е, пятитонного – 5000 у.е. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной, если для приобретения автомашин выделено 150 тысяч рублей? Задачу решить графическим и аналитическим методами. Решение. Пусть приобретено 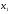 трехтонных и трехтонных и 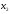 пятитонных пятитонныхавтомашин. Из условия задачи имеем
0 ≤ 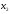 ≤ 18 ≤ 18 4 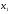 + 5 + 5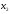 = 150 . (24) = 150 . (24)Суммарная грузоподъемность приобретенных грузовиков равна L = 3 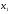 + 5 + 5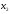 . (25) . (25)Задача состоит в нахождении такого решения системы (24) , при котором линейная форма (целевая функция) (25) принимает наибольшее значение. Графический метод решения. В прямоугольной системе координат 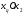 построим многоугольник построим многоугольникOABCD, образованный прямыми 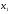 = 0 (OD), = 0 (OD), 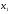 =20 (AB), =20 (AB), 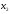 = = = 0 (AO), 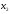 = 18 ( CD), 4 = 18 ( CD), 4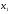 + 5 + 5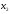 = 150 ( BC) и прямую 3 = 150 ( BC) и прямую 3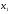 + 5 + 5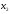 = 0 (l) ( рис. 2.9 ). = 0 (l) ( рис. 2.9 ).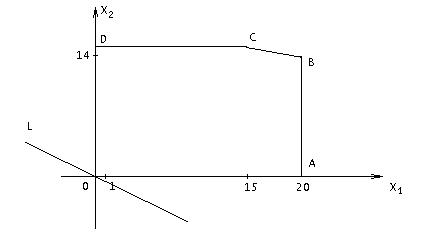 Рис. 2.9. Решение задачи 23 графическим методом Системе (24) удовлетворяют координаты точек, лежащих на пятиугольнике OABCD и внутри него. Так как прямые (24) и BC не параллельны, то для нахождения оптимального решения системы (24), для которого линейная форма (25) принимает наибольшее значение, достаточно найти значения этой формы в точках A, B, C, D и из полученных чисел выбрать наибольшее. В нашей задаче эти точки имеют следующие координаты: А (20; 0), В (20; 14), С (15, 18), D (0; 18). Подставляя координаты этих точек в (25), получим: L (A) = L (20; 0 ) = 60; L (B) = L (20; 14) = 130; L (C) = L (15; 18) = 135; L (D) = L (0; 18) = 90. Следовательно, L = L (15; 18) = 135, то есть предприятию следует приобрести 15 трехтонных и 18 пятитонных автомашин, при их общей грузоподъемностью 135 т. 3.5.1. Вопросы для самопроверки
|

 , sinx, cosx,
, sinx, cosx,