ЕН.Р.1 Фин вычисления. Учебнометодический комплекс дисциплины Финансовые вычисления 080109. 65 Бухгалтерский учет, анализ и аудит Форма подготовки (заочная)
 Скачать 1.86 Mb.
|
|
Rp = Rf + [(Rm - Rf)/   ]*  ,Где Rp – ожидаемая доходность портфеля, состоящего из рисковых и безрисковых активов, величина (Rm - Rf)/ характеризует тангенс угла наклона линии рынка капитала.Ранее нами были рассмотрены понятия систематического (недиверсифицируемого) и несистематического (диверсифицируемого) риска. Для измерения систематического риска используется показатель бета. Нулевое значение бета соответствует отсутствию систематического риска, а бета равное единице - систематическому риску рыночного портфеля. Если известен показатель бета актива, то его доходность в рамках модели CAPM может быть определена из следующего соотношения: Ri = Rf + βi * (Rm - Rf), Где Ri – ожидаемая доходность актива, Rm, Rf – доходность рыночного портфеля и безрисковая доходность, βi – бета коэффициент актива. Бета коэффициент акций или других ценных бумаг рассчитывается как отношение ковариации актива и рыночного портфеля и дисперсии рыночного портфеля: βi =  / 2.Числитель представляет вклад индивидуального актива I в величину риска диверсифицированного портфеля, а знаменатель – величину риска рыночного портфеля. Таким образом, бета измеряет систематический риск относительно риска рынка в целом. Пример. Рассмотрим процедуру вычисления бета коэффициента на примере компании Макдоналдс. В колонках 2 и 3 представлены данные по годовой доходности за 9 лет для акций компании Макдоналдс и для рынка в целом. В колонках 4 и 5 представлены разности между текущей доходностью и средней доходностью. Так, например, значение -0,1113 в колонке 4 для 1977 года получается путем вычитания из доходности акций Макдоналдс в 1997 году равной -0,0388 среднего значения доходности равной 0,0725. В колонке 6 представлены квадраты отклонения ежегодной доходности рынка от среднего значения, а в колонке 7 – произведения ежегодных отклонений доходности акций Макдоналдс и рынка.
Ковариация доходности акций Макдоналдс и рынка будет равна CV(Rmd, Rm) = 0,1480/9 = 0,0164. Далее определяем дисперсию рынка. 2.= 0,1317/9 = 0,0146.Бета коэффициент акций Макдоналдс найдем из следующего соотношения: βi = CV(Rmd,Rm) / 2 = 0,0164/0,0146 = 1,123Коэффициент бета (  -коэффициента) характеризует склонность актива «двигаться» вместе со всем рынком. Иными словами характеризующего степень ее изменчивости по отношению к «средней акции», в качестве которой рассматривается акция, стремящаяся «двигаться» синхронно со всем рынком акций. Это означает, что если доходность по рынку в целом увеличивается на 10%, то доходность «средней акции» возрастает в такой же степени, и, наоборот – при падении – падает. Портфель акций с - коэффициентом, равным единице, будет иметь такую же степень риска, как и весь рынок. Если для акции = 0,5, это означает, что ее доходность будет повышаться или падать вдвое меньше, чем у всего рынка. Портфель акций с таким -коэффициентом будет иметь вдвое меньшую степень риска по сравнению с портфелем, имеющим =1. В то же время если акция имеет = 2, то ее подвижность вдвое выше, чем у средней акции. Важным свойством - коэффициента является то, что портфеля вычисляется как взвешенная сумма - коэффициентов составляющих его активов. При этом следует помнить, что общий риск портфеля не является взвешенной суммой составляющих его активов. Обусловлено это тем, что бета измеряет только систематический риск актива, который не является диверсифицируемым.Исходя из вышесказанного для расчета -коэффициента портфеля акций может быть использовано следующее соотношение p = 1*W1+ 2*W2+… + n*Wn,Например, инвестор имеет 40 тыс. долл. и сформировал портфель из четырех акций, вложив в каждый вид акций по 10 тыс. долл. Если каждая акция имеет = 0,8, то бета такого портфеля также будет равен 0,8: p = 0,8 х 0,25 + 0,8 х 0,25 + 0,8 х 0,25 = 0,8.Такой портфель будет менее рисковым, чем весь рынок акций, и будет испытывать меньшее колебание доходности по сравнению со всем рынком. Теперь представим, что одна из акций продана и заменена акцией, имеющей = 2, тогда риск портфеля увеличится и его бета возрастет: p = 0,8 х 0,25 + 0,8 х 0,25 + 0,8 х 0,25 + 2,0 х 0,25 =1,1.Если одну из акций заменить на акцию с = 0,2, то бета портфеля снизится и составит: p = 0,8 х 0,25 + 0,8 х 0,25 + 0,8 х 0,25 + 0,2 х 0,25 = 0,65.Таким образом, риск портфеля может быть снижен путем включения в портфель акций, имеющих низкое значение -коэффициента.В таблице представлены -коэффициенты некоторых отечественных и зарубежных компаний.
Опционы Сущность опциона, основные понятия В последнее десятилетие заметно усилилось внимание к так называемым производным финансовым инструментам (derivativesecurities). Термин "производный" связан с тем, что стоимость такого инструмента как бы привязывается к стоимости того или иного базисного финансового инструмента (underlyingsecurities) и становится по отношению к нему производной величиной. Под опционом (options) понимают право, но не обязательство, купить/продать некоторые финансовые инструменты, акции или валюту по оговоренной цене при наступлении срока или до него. Опционы используются также и при приобретении реальных активов. Так, например, при покупке или аренде земли, приобретении крупных активов корпорации часто покупают опцион на возможность дополнительного приобретения этих активов. Это дает возможность при расширении деятельности зафиксировать цену активов. При эмиссии ценных бумаг корпорации часто оговаривают возможность их выкупа. В ряде контрактов на поставку, страховых, трудовых и пр. оговаривается возможность сторон прекратить договор или изменить его условия. Все эти права также являются опционами. Организованная торговля опционами началась в 1973 году и в настоящее время опционы являются важнейшим инструментом управления рисками. Таким образом, опцион представляет собой контракт, дающий право его владельцу совершить сделку или отказаться от нее. К условиям контракта чаще всего относятся цена сделки и время ее завершения. За получение этого права покупатель опциона (buyer, holder) при заключении контракта уплачивает продавцу (seller, writer) некоторую премию (premium). Последняя представляет собой рыночную цену опциона. Таким образом, само право в этой операции становится товаром. Различают опционы на право покупки (calloption) и на право продажи (putoption). Для сокращения записи, опцион на право покупки часто называют опцион колл, опцион на право продажи - опцион пут. Опцион, который может быть реализован только в оговоренный в контракте день, день исполнения (expirationday, dayofmaturity), называют европейским. Если предусматривается возможность исполнения опциона в любой момент до этого дня, то такой опцион называют американским. Заметим, что приведенные названия не определяют место сделки. Например, американский опцион может быть куплен и в Европе. Оговоренная в контракте цена объекта опциона называется объявленной, договорной ценой, или ценой исполнения (strikingprice, exerciseprice). Можно сказать, что опцион является особым случаем форвардной операции. Он отличается от форвардной операции прежде всего тем, что владелец опциона может реализовать свое право на сделку или отказаться от ее исполнения. Если сделка не исполняется (отказ от исполнения), то владелец опциона несет потери только в размере выплаченной им премии. Охарактеризуем опционы колл и пут с позиций как покупателя, так и продавца. Исполнение опциона может быть реализовано в нескольких вариантах. Рассмотрим их применительно к опциону колл при покупке акции. Если есть основание ожидать, что цена акций компании Gбудет расти (оптимистический прогноз) в течение некоторого периода, то инвестор может купить опцион колл. Пусть условия опциона таковы: цена исполнения 900, премия 50. Допустим в день исполнения рыночная цена акции оказалась равной 1050. Владелец опциона использует свое право и покупает их по цене исполнения, получая прибыль в размере 1050 - (900 + 50) = 100 на одну акцию. Таким образом, опцион реализуется и приносит доход. Опцион может быть реализован и без непосредственной покупки акции — путем получения владельцем опциона разности между рыночной ценой акции и ценой исполнения. Если рыночная цена акции равна 950, то прибыль инвестора будет нулевая: 950 - (900 + 50) = 0. В этом случае для владельца опциона безразлично, купить ли акцию на рынке без опциона или использовать опцион. В обоих решениях его издержки одинаковы. Наконец, при цене ниже 950 покупатель отказывается от исполнения опциона и несет убытки. Таким образом, в данном примере максимальный убыток равен премии – 50 рублей, а размер прибыли не ограничен. Приведенный пример иллюстрируется на графике "прибыль - рыночная цена акции" (см. рис.). Следует обратить внимание на то, что приведенные расчеты прибыли не учитывают разновременность расходов владельца опциона, т.е. премия выплачивается при покупке опциона, а покупка акции осуществляется в день исполнения. Обратимся к положению продавца опциона колл в этой сделке. Очевидно, что прибыль/потери продавца опциона "симметричны" потерям/прибыли покупателя опциона: там, где у покупателя — доход, у продавца — потеря, и наоборот. Максимальная прибыль равна 50, размер убытка не ограничен. Если цена акции компании Gпревышает 950, то продавец несет убытки (см. рис.). 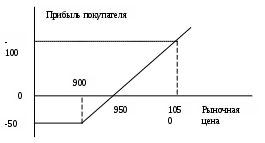 Рис. График зависимости прибыли покупателя от рыночной цены 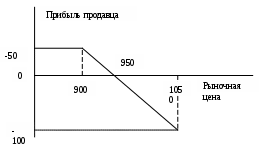 Рис. График зависимости прибыли продавца от рыночной цены Перейдем к опционам пут (напомним, что это опцион на право продажи). Пусть ожидается падение цены акций компании G(пессимистический прогноз). В этой ситуации можно продать опцион колл. Однако, как только что было показано, позиция продавца оказывается довольно рискованной. Вместо этого он предпочитает купить опцион пут. Условия опциона: цена исполнения 870, премия 40. Картина зависимости "прибыль—цена акции" для покупателя опциона пут в этой ситуации кардинальным образом меняется. Если рыночная цена акции меньше 870 - 40 = 830, то покупатель опциона имеет прибыль. Например, при цене акции 810 прибыль составит 870 - (810 + 40) = 20. При цене 830 прибыль нулевая, так как 870 - (830 + 40) = 0, а при цене, превышающей 830, имеет место убыток, максимальная величина которого составляет 40. Как было показано, положения покупателя и продавца опциона в отношении прибыли являются "зеркальными отображениями". Различаются они и по моменту получения ожидаемой прибыли. Продавец получает ее немедленно, покупатель — в момент реализации опциона. Приведем пример валютного опциона. Ограничимся при этом позицией покупателя опциона колл. Пример 1. Импортер, который имеет рубли и в будущем должен выплатить некоторую сумму в долларах США, приобретает опцион на право покупки долларов по курсу 1 долл. США = 28 рублей и выплачивает премию 0,5 рубля за 1 долл. При наступлении срока валютирования возможны следующие варианты завершения операции, определяемые движением курса доллара. 1. Курс доллара упал до 27 рублей. В этом случае покупатель не использует опцион и покупает доллары на рынке. Его результаты: разность между курсом опциона и рыночным курсом: 28-27=1,0 премия: -0,5 условная прибыль от опциона в расчете на 1 долл.: 0,5 2. Курс доллара вырос до 29 рублей. Покупатель опциона использует свое право на покупку валюты по цене исполнения (оговоренному курсу). Результат: реальная прибыль в размере 29 - (28 + 0,5) = 0,5 рубля на 1 долл. Курс равен 28. Покупатель опциона может его использовать или отказаться от него и купить валюту на рынке. В обоих случаях его расходы равны 28,5, т.е. потери относительно рыночного курса равны премии (0,5). Курс превышает цену исполнения, но это превышение меньше премии. Если покупатель все же реализует опцион, то потери также меньше премии. Пусть курс равен 28,3, потери равны 28,3 - 28,5 = 0,2 на 1 долл. Приобретение права на покупку объекта опциона имеет смысл при ожидании повышения его цены. Право на продажу, очевидно, покупается при ожидании снижения цены. Как видно из приведенных рисунков, область изменения рыночной цены акции делится на два интервала, доходный (inthemoney) и бездоходный (outthemoney), разделяемые ценой исполнения сделки. Для опциона колл в доходном интервале рыночная цена больше цены исполнения, их разность положительна (на рис. интервал цен, превышающих 950). В бездоходном интервале разность рыночной цены и цены исполнения отрицательна. Наконец, при равенстве рыночной цены цене исполнения имеем так называемый нейтральный опцион (atthemoney). Аналогичные по содержанию интервалы можно выделить и при покупке опциона пут. Ограниченные потери и теоретически неограниченный доход делают опционы привлекательным инструментом для инвесторов. Помимо простых схем опциона, которые были только что охарактеризованы, на практике прибегают и к более сложным, комбинированным схемам. Такие схемы предполагают одновременную покупку двух, трех опционов с различными характеристиками. Основное назначение комбинированных схем — гарантирование владельца опциона от значительных потерь. Например, одновременно покупается и продается опцион колл по разным ценам исполнения и с различными премиями, одновременно используются опционы пут и колл при одинаковой или различных ценах исполнения, двух опционов колл с различными ценами исполнения и одного опциона пут и т.д. Естественно, что чем больше простых опционов охватывает комбинированная схема, тем сложнее ее осуществить - труднее найти контрагентов по сделке. Цена опциона, модель Блека—Шоулза Как было показано выше, реальные прибыль или потери от опциона для обеих участвующих сторон зависят от цены исполнения, рыночной цены актива на момент исполнения опциона и премии. В условиях развитого рынка опционов цена исполнения устанавливается на бирже опционов. Обычно это величина, близкая к текущей рыночной цене актива. Если биржа опционов отсутствует, то единственный путь установления цены исполнения — непосредственная договоренность покупателя и продавца опциона. Предлагаемая продавцом цена должна быть конкурентоспособной и в то же время обеспечить ему некоторую прибыль. Опционы представляют определенный интерес не только в практическом плане, но и в теоретическом — с позиции количественного анализа, который осуществляется с помощью разработки специальных моделей (optionmodels), описывающих взаимосвязи основных параметров опционов. Следует, однако, заметить, что теоретические цены опционов, полученные по моделям, в силу неполноты учета экономических условий и их изменчивости, условности входящих статистических данных, как правило, отличаются от рыночных. Вместе с тем, принято считать, что если рыночная цена опциона сильно занижена относительно теоретической цены, то есть основание для его покупки. Наиболее известной моделью определения цены опциона является модель Блека—Шоулза (Black—Scholes). Рассмотрим ее применительно к опционам колл для обыкновенных акций. Ранее мы говорилось о том, что цены опционов определяются на рынке и зависят от ряда известных и неизвестных на момент его покупки параметров. К их числу следует отнести: текущая цена базисного инструмента, уровень цены исполнения, стандартное отклонение доходности базисного инструмента, срок исполнения опциона, размер безрисковой ставки. Одной из наиболее важных зависимостей в моделях ценообразования опционов является зависимость между ценной опциона и ценой базисного актива. 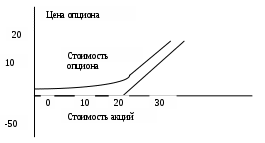 При низкой стоимости базисного актива относительно цены исполнения цена опциона является также низкой и имеет тенденцию незначительного роста при росте стоимости базисного актива. На данном рисунке цена исполнения опциона составляет 20 рублей. Если цена акций растет, но остается существенно меньшей цены исполнения, то это не приводит к существенному росту цены опциона. Если цена акций существенно превышает цену исполнения, то цена опциона изменяется в соответствие с изменением цены базисного актива. Вторым параметром, определяющим цену опциона, является цена его исполнения. Она остается постоянной в течение времени жизни опциона. В модели Блека—Шоулза цена опциона и цена исполнения связаны обратной зависимостью. Обусловлено это тем, что опцион становится прибыльным только в том случае, если цена базисного актива превышает цену исполнения. Третьим параметром является стандартное отклонение доходности базисного актива. В модели Блека—Шоулза цена опциона возрастает при росте стандартного отклонения и соответственно риска базисного актива. Такой характер зависимости обусловлен тем, что опцион является финансовым инструментом с неограниченным потенциалом прибыльности при ограниченных возможностях потерь. В результате при возрастании изменчивости (волатильности) базисного инструмента возможности получения большей прибыли увеличиваются. При этом возможные потери остаются на прежнем уровне. Четвертым параметром в модели Блека—Шоулза является срок исполнения опциона. Поскольку большинство опционов позволяют их держателям исполнить опцион в любой момент в течение срока его жизни, то их цена связана со сроком исполнения прямой зависимостью. Более длительный срок исполнения создает большие возможности для повышения цены базисного актива. Последним параметром в модели Блека—Шоулза является размер безрисковой ставки. Для понимания влияния данного параметра на цену опциона рассмотрим следующий пример. Предположим, что вы ожидаете рост стоимости акций в будущем и решили их приобрести. Инвестиции при этом могут быть произведены как в сами акции, так и в опцион на их приобретение. Если вы инвестируете средства в акции, то ваши инвестиции будут соответствовать текущей стоимости акций. Если вы приобретаете опцион, то текущие инвестиции будут равны цене опциона, а будущие – цене исполнения. Таким образом при приобретении опциона вы фактически откладываете оплату приобретаемых акций на будущее. В результате при повышении безрисковой ставки эффективность приобретения опциона увеличивается. Все названные факторы учитываются в формуле Блека—Шоулза. CALL = P* N(d1) – E*e-rt * N(d2) Где: CALL — цена опциона, P — текущая цена акции, Е — цена исполнения, e-rt — дисконтный множитель на срок tпо непрерывной ставке? t — срок до даты исполнения, r — непрерывная процентная ставка, принятая для дисконтирования, N(d1) и N(d2) — функции нормального распределения, d1 = [ln(P/E)+(r+0,5*  2)*t]/( √ t),d2 = d1 - √ tВеличина E*e-rt представляет собой дисконтированную на момент покупки опциона цену исполнения. Функции нормального распределения (плотности вероятности) определяются для параметров d1и d2. Пример 1. Колл опцион дает право на приобретение акций компании А по цене 20 рублей за штуку. До срока исполнения остается 0,5 года. Безрисковая ставка равна 5% и стандартное отклонение доходности акций составляет 0,3. Стоимость акций в настоящее время составляет 25 рублей за штуку. Необходимо определить цену опциона. Шаг 1. Рассчитываем значения величин d1и d2. d1 = [ln(P/E)+(r+0,5* 2)*t]/( √ t),d1 = [ln(25/20)+(0,05+0,5*0,045)*0,5]/(0,3√ 0,5), d1 = [0,22314+0,095*0,5]/0,2121 d1 = 1,276. d2 = d1 - √ td2 = 1,276 – 0,3 * √ 0,5 d2 = 1,064. Шаг 2. Рассчитываем значения N(d1) и N(d2). Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере N(d1) = 0,899, N(d2).= 0,8563. Шаг 3 Рассчитываем стоимость опциона CALL = P* N(d1) – E*e-rt * N(d2) CALL = 25* 0,899 – 20*e-0,05*0,5 * 0,8563 = 5,77. Пример 2. 4 октября 200 г. цена закрытия опциона компании Х со сроком исполнения 21 апреля 2001 г. и ценой исполнения $49 составила $4. Базовые акции продаются по цене $50. 4 октября срок до исполнения составляет 199 дней. Непрерывно начисляемая безрисковая ставка равна 7%. Дисперсия доходности акций составляет 0,09. Шаг 1. . Рассчитываем значения величин d1и d2. d1 = [ln(P/E)+(r+0,5* 2)*t]/( √ t),d1 = [ln(50/49)+(0,07+0,5*0,09)*199/365]/(√0,09*199/365) = 0,3742 d2 = d1 - √ td2 = 0,3742 - √0,09*199/365 = 0,1527. Шаг 2. Рассчитываем значения N(d1) и N(d2). Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере N(d1) = 0,6459 и N(d2) = 0,5607 Шаг 3 Рассчитываем стоимость опциона CALL = P* N(d1) – E*e-rt * N(d2) CALL = 50* 0,6459 – 49*e-0,07*199/365 * 0,5607= 5,85. Таким образом, цена опциона, полученная с помощью модели Блэка-Шоулза оказалась выше, чем цена на рынке. Это означает, что опцион недооценен и для инвестора целесообразно приобретение данного опциона. ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Дальневосточный государственный технический университет (ДВПИ имени В.В.Куйбышева) Дальнереченский социально-экономический институт (филиал) |