Пособие по общей статистике. Учебнометодическое пособие для студентов очной формы обучения по специальности Таможенное дело

• Название: Учебнометодическое пособие для студентов очной формы обучения по специальности Таможенное дело
• Дата: 16.06.2019
• Размер: 214.4 Kb.
• Имя файла: Пособие по общей статистике.docx
• Тип: Учебно-методическое пособие; #81928
• страница: 3 из 9

Тема 6. Формы и виды статистических показателей.

Абсолютные показатели. Виды абсолютных показателей и их значение в статистическом исследовании. Единицы измерения абсолютных показателей.

Относительные показатели. Виды относительных показатели (показатели динамики, координации, структуры, сравнения, интенсивности). Средние величины. Формы и виды средних величин. Средняя арифметическая величина и ее свойства. Структурные средние. Показатели вариации. Размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Свойства дисперсии. Показатели, характеризующие форму распределения. Использование статистических функций MS EXCEL для расчета статистических показателей.

Контрольные вопросы по теме 6:

1. 
   Назовите сущность и виды обобщающих статистических показателей.
   
2. 
   Что называют абсолютными показателями в статистике? Приведите пример.
   
3. 
   Приведите пример условно-натуральной величины.
   
4. 
   Какими бывают абсолютные величины в статистике в зависимости от единиц измерения?
   
5. 
   Назовите виды относительных показателей. Приведите пример.
   
6. 
   Охарактеризуйте каждый относительный показатель.
   
7. 
   Что выражают относительные величины структуры и координации.
   
8. 
   Для характеристики каких явлений используют относительные величины интенсивности и сравнения.
   
9. 
   Перечислите степенные средние в порядке возрастания их значения.
   
10. 
    Какие Вы знаете структурные средние?
    
11. 
    Приведите определение медианы.
    
12. 
    Какое значение признака называется модальным?
    
13. 
    Что такое мода?
    
14. 
    Каким образом осуществить графическое определение моды и медианы?
    
15. 
    Какие функции MS EXCEL используют для расчета статистических показателей?
    

Тесты по теме 6:

1. Статистический показатель - это

а) размер изучаемого явления в натуральных единицах измерения

б) количественная характеристика свойств в единстве с их качественной определенностью

в) результат измерения свойств изучаемого объекта

2. Чтобы получить относительный показатель динамики с переменной базой сравнения для i-го периода, необходимо:

а) перемножить относительные показатели динамики с постоянной базой сравнения за i-й и (i – 1) периоды;

б) разделить относительный показатель динамики с постоянной базой сравнения за i-й период на аналогичный показатель за период (i – 1);

в) разделить относительный показатель динамики с постоянной базой сравнения за i-й период на аналогичный показатель за период (i + 1).

3.Относительный показатель реализации предприятием плана производства продукции составил 103 %, при этом объем производства по сравнению с предшествующим периодом вырос на 2 %. Что предусматривалось планом?

а) снижение объема производства;

б) рост объема производства.

4. Сумма относительных показателей координации, рассчитанных по одной совокупности, должна быть:

а) строго равной 100;

б) меньше 100 или равной 100;

в) меньше, больше или равной 100.

5. Средние величины – это:

а) обобщающие показатели, которые характеризуют типовой уровень вариационного признака единицы неоднородной совокупности;

б) обобщающие числовые характеристики изучаемого количественного признака по всем единицам статистической совокупности;

в) средний уровень вариационного ряда распределения единиц совокупности по количественному признаку;

г) нет верного ответа.

6. К степенным средним относятся следующие виды:

а) арифметическая;

б) хронологическая;

в) мода;

г) гармоническая.

7. Средние величины измеряются

а) в тех же единицах измерения, что и варианты X;

б) в коэффициентах;

в) в процентах;

г) свой ответ.

8. Если каждое значение признака X встречается один раз или значение f=1, то применяется:

а) средняя арифметическая взвешенная;

б) гармоническая простая;

в) хронологическая;

г) свой ответ.

9. Если значение признака X умножить на 5, то средняя арифметическая:

а) не изменится;

б) уменьшиться на 5;

в) увеличится на 5;

г) увеличится в 5 раз.

10. Если все частоты разделить на 3, то средняя арифметическая:

а) не изменится;

б) уменьшиться на 3;

в) увеличится на 3;

г) увеличится в 3 раз.

11. Если даны размеры минимального и максимального выигрыша, то для расчета среднего значения необходимо применить:

а) среднюю арифметическую;

б) среднюю гармоническую;

в) среднюю квадратическую;

г) среднюю геометрическую.

12. Дана численность работников на 01.01, 01.02, 01.03, 01.04, 01.05, 01.06. Для расчета средней численности работников необходимо использовать:

а) среднюю арифметическую взвешенную;

б) гармоническую простую;

в) хронологическую;

г) гармоническую взвешенную.

13. Имеются данные о распределении рабочих цеха по стажу работу. Каков средний стаж работы рабочего?

Стаж работы, лет	До 5	5 – 10	10 – 15	15 – 20	20 и выше
Количество рабочих, чел	10	20	5	12	3

а) 5 лет;

б) 12 лет;

в) 10,3 лет;

г) 11,5 лет.

14. Если в исходных данных дана урожайность отдельных культур, ц/га и валовый сбор сельскохозяйственных культур со всей площади, то для расчета средней урожайности необходимо воспользоваться:

а) средней арифметической взвешенной;

б) гармонической простой;

в) хронологической;

г) гармонической взвешенной.

15. Для характеристики наиболее часто встречающегося значения признака применяется:

а) медиана;

б) мода;

в) средняя кубическая;

г) свой ответ.

16. Варианта, которая делит вариационный ряд пополам – это:

а) медиана;

б) мода;

в) средняя кубическая;

г) свой ответ.

17. Даны данные о распределении студентов группе по росту в следующей таблице:

Рост, см	165	170	175	182	185
Число студентов, чел.	6	8	11	3	1

Найти номер варианты, являющейся медианой и размер медианы.

Задачи по теме 6:

Задача 1

Имеются данные по 2 заводам различных отраслей промышленности

Таблица 3

Затраты на производство продукции	Металлургический завод		Машиностроительный  завод
млн. руб.	базисный	текущий	базисный	текущий
Всего	44,7	46,0	46,6	48,7
Сырье и основные материалы	25,2	25,5	24,5	24,8
Вспомогательные материалы	2,7	2,9	3,3	3,6
Топливо	5,0	5,2	6,3	6,6
Энергия	1,8	1,9	2,2	2,5
Амортизация	3,2	3,4	4,3	4,6
Заработная плата и отчисления на соцстрах.	5,4	5,6	5	5,3
Прочие расходы	1,4	1,5	1	1,3

 1.Используя функции MS EXCEL, вычислить относительные показатели структуры по каждому заводу и 2 заводам вместе в текущем году, относительные показатели динамики по каждому заводу и 2 заводам вместе и относительные показатели сравнения.

2. 
   Изобразить графически результаты в MS EXCEL.
   

Задача 2

Определить общее производство моющих средств в условных тоннах (условная жирность 40%) по плану и фактически, а также процент выполнения плана по следующим данным:

Вид продукта	Жирность, %	физическая масса, т
		По плану	фактически
Мыло хозяйственное	60	500	600
Мыло туалетное	80	1000	1500
Стиральный порошок	10	50000	40000

Задача 3 По данным о численности жителей двух крупнейших городов России (тыс. чел) определить индексы сравнения и динамики.

Город /Год	2004	2005
Москва	10391	10407
Санкт-Петербург	4624	4600

Задача 4

1. По плану на 2005 год намечалось увеличение товарооборота на 3%. В 2005 году плановое задание перевыполнили на 600 млн. руб. или на 2,5%. Определить фактический прирост товарооборота (в млн. руб.) в 2005 году по сравнению с 2004 годом.

2. По данным о товарообороте из предыдущей задачи, состоящего из реализации собственной продукции и продажи покупных товаров, определить относительные величины координации и структуры собственной и покупной продукции в 2004 и 2005 годах, если известно, что доля собственной продукции в 2004 году составила 65%, а в 2005 году она увеличилась на 10%.
Задача 5

Добыча нефти и угля в РФ в 1999-2001 гг. характеризуется следующими данными:

Топливо	Объем добычи, млн. т
	1999	2000	2001
Нефть Уголь	305 250	324 258	348 269

Теплота сгорания нефти равна 45,0 мДж/кг,угля – 26,8 мДж/кг. Сделайте пересчет в условное топливо (29,3 мДж/кг) и проведите анализ изменения совокупной добычи этих ресурсов.
Задача 6

Имеются данные о внешнеторговом обороте России со странами СНГ:

	2000	2001
Экспорт Импорт	91,3 31,5	87,7 40,3

Вычислите относительные показатели структуры и координации. По результатам расчетов сформулируйте выводы.
Задача 7

Использование складских помещений города характеризуется следующими данными:

Группы складских помещений по площади, тыс. м2	Число помещений	Общая занятая площадь, тыс. м2
До 5 5-10 10-15 15-20 20-25 25-30 30-35 Более 35	3 21 17 9 5 3 4 2	5,2 108,0 163,6 101,2 65,3 40,6 55,4 29,0

Вычислите:

А) средний процент загрузки складских помещений по каждой группе;

Б) средний процент загрузки складских помещений в целом по городу.
Тема 7 Показатели вариации. Изменчивость.

Виды показателей вариации. Свойства и методы расчета дисперсии. Дисперсия альтернативного признака. Правило сложения дисперсий. Закономерности ассиметрии. Коэффициент ассиметрии. Нормальное распределение и его характеристики. Моменты распределения. Показатели формы распределения.
Контрольные вопросы по теме 7:

1. 
   Для чего нужны показатели вариации?
   
2. 
   Какие показатели относятся к показателям вариации?
   
3. 
   Какой признак называется альтернативным?
   
4. 
   Чему равны средняя и дисперсия альтернативного признака?
   
5. 
   Приведите правило сложения дисперсий.
   
6. 
   Приведите характеристики нормального распределения.
   

Тесты по теме 7:

1. Вариация – это:

а) изменение массовых явлений во времени;

б) изменение структуры статистической совокупности в пространстве;

в) изменение значений признака во времени и в пространстве;

г) изменение состава совокупности.

2. Что характеризует коэффициент вариации?

а) диапазон вариации признака;

б) степень вариации признака;

в) тесноту связи между признаками;

г) пределы колеблемости признака.

3. Если все значения признака увеличить в 16 раз, то дисперсия:

а) не изменится;

б) увеличится в 16 раз;

в) увеличится в 256 раз;

г) увеличится в 4 раза;

д) предсказать изменение дисперсии нельзя.

4. Чему равна межгрупповая дисперсия, если отсутствуют различия между вариантами внутри групп?

а) единице;

б) нулю;

в) колеблется от нуля до единицы;

г) общей дисперсии;

д) средней из групповых дисперсий.

5. Чему равна межгрупповая дисперсия, если отсутствуют различия между вариантами внутри групп?

а) единице;

б) нулю;

в) колеблется от нуля до единицы;

г) общей дисперсии;

д) средней из групповых

6. Что характеризует коэффициент вариации?

а) диапазон вариации признака;

б) степень вариации признака;

в) тесноту связи между признаками;

г) пределы колеблемости признака.

7. Средний размер реализованной коммерческой организацией спортивной обуви равен 39, мода – 39, медиана – 39. На основании этого можно сделать вывод, что распределение проданной спортивной обуви по размеру:

а) симметричное;

б) приближенно симметричное;

с) с левосторонней асимметрией;

г) с правосторонней асимметрией;

д) данные не позволяют сделать вывод.

8. Статистическая совокупность из 245 единиц разделена на 16 групп. Число степеней свободы для критерия 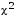равно:

а) 244;

б) 242;

в) 16;

г) 15;

д) 13.

9. Теоретическая кривая распределения – это:

а) средний квадрат отклонений;

б) значения признака, делящие совокупность на равные части;

в) кривая, выражающая закономерность распределения, исключающая влияние случайных факторов;

г) закономерности изменения частот в вариационных рядах.

Задачи по теме 7:

Задача 1

Имеются данные о распределении количества деталей по числу работающих:

Количество деталей, шт.	7	1	6	3	8	5	Итого
Число работающих % к итогу	10	26	29	17	13	5	100

Используя центральные моменты первых четырех порядков, рассчитайте коэффициенты асимметрии и эксцесса. Сделайте выводы.

Задача 2

Распределение магазинов по размеру товарооборота за октябрь 2004 г. характеризуется следующими данными:

Группы магазинов по размеру товарооборота, тыс. руб.	Число магазинов	Группы магазинов по размеру товарооборота, тыс. руб.	Число магазинов
До 200	12	500-600	15
200-300	14	600-700	7
300-400	18	700-800	6
400-500	23	Свыше 800	4
Итого	-	—	100

Определите показатели асимметрии и эксцесса распределения магазинов по размеру товарооборота. Сделайте выводы.

Задача 3

По данным таблицы вычислите среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сделайте выводы.

Курс продажи акций, руб.	Кол-во проданных акций, шт.
1092	488
1059	309
1150	105

Задача 4

Имеются данные о чистой прибыли (балансовой за вычетом налогов) предприятий двух районов:

Район	Число предприятий	Чистая прибыль, млн. р.
1	6	4, 6, 9, 4, 7, 6
2	10	8, 12, 8, 9, 6, 5, 7, 7, 8, 10

Определите:

1. Дисперсии чистой прибыли: групповые, среднюю из групповых, межгрупповую, общую.

2. Коэффициент детерминации и корреляционное отношение.

Сделайте выводы.
Задача 5

По нижеследующим данным вычислите показатели степени вариации, сделайте

выводы.

Группы деталей по весу, г.	40-50	50-60	60-70	70-80	80-90	90-100	100-110	110-120	Итого
Число Деталей	2	4	12	18	21	24	11	8	100

Задача 6

В трех магазинах 16 июля 2000 года были проданы кроссовки следующих размеров:

Размер	40	41	42	43	44	45
Магазин № 1	18	10	2	35	20	15
Магазин № 2	2	21	15	17	15	10
Магазин № 3	17	6	20	40	12	15

1. Изобразите данные в виде полигонов распределения и суммарный.

2. Вычислите дисперсии (общую, групповые, межгрупповую).

3. Рассчитайте коэффициенты вариации.

4. Найти моду и медиану суммарного распределения.
Задача 7

Для статистической совокупности; 5, 4, 4, 2, 0, 2, 5, 2, 2, 4 вычислить коэффициент вариации и построить полигон частот.