ОТН - ПР 3 Мат. обраб. Эспон. законе. Учебнометодическое пособие для выполнения практических работ по дисциплинам Основы надежности

• Название: Учебнометодическое пособие для выполнения практических работ по дисциплинам Основы надежности
• Дата: 13.11.2022
• Размер: 109.58 Kb.
• Имя файла: ОТН - ПР 3 Мат. обраб. Эспон. законе.docx
• Тип: Учебно-методическое пособие; #786773
• страница: 4 из 19

среднеквадратическая ошибка определения среднеквадратического отклонения

(t)= (6)

Тогда, округляя значения отклонений, получим
M(t)= 75 ± 8 (ч).
Нарисунке1 для построения гистограммы по оси абсцисс tоткладываются интервалы t_i(см. таблицу 2, колонка 2) случайной величины t_iи на каждом из интервалов строится прямоугольник с площадью, равной частоте появления случайной величины в данном интервале.

Высоты прямоугольников пропорциональны соответствующим частотам и равны эмпирической плотности вероятности [n_i/(nt_i)](см. таблицу 2, данные колонки 9) для каждого интервала. На рисунке 1 представлена точечная гистограмма распределения, где значения статистической вероятности отложены от середины каждого интервала.

Исходя из характера гистограммы, можно предположить, что исследуемая случайная величина распределена по экспоненциальному закону. Об этом свидетельствует также почти полное совпадение по величине математического ожидания M(t)= 75 ч и среднеквадратического отклонения

(t)= 80 ч случайной величины t(коэффициент вариации V 1).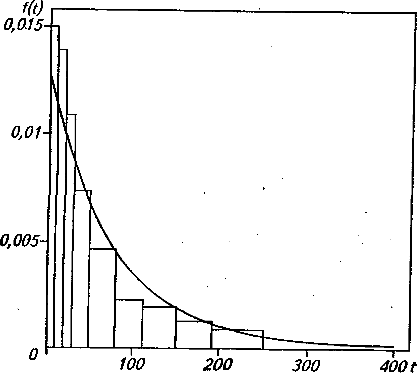

Выравнивающий график функции ƒ(t) строим по данным таблицы 3 (колонка 5).

Рисунок 1 – Гистограмма наработки на отказ и выравнивающая кривая Приняв в качестве математического ожидания наработки на отказ его

оценку (статистическое среднее) M(t)= 75 ч, можно записать

ƒ(t)=· , или ƒ(t)=·exp(-·t_i). (7) Поскольку при экспоненциальном законе распределения

 = 1/ M(t)= const, то

ƒ(t)=·exp(-·t_i)= 0,013·е^-0,013·t , (8)

где  = 1/ M(t)=1 /75 =0,013.

В таблице 3 приведены следующие результаты расчетов:

В колонке 2 значение t_i(гран.)границы интервалов из колонки 2 таблицы 2. Вколонке 3 значения ·t_i.

Вколонке4 функции (е^{- ·t})можно определить, используя таблицу е^-х

приложения А.
Та6лица 3 - Теоретические значения вероятностей

№	ti (гран.)	 ·ti	е-0,013·t	ƒ(t)		n·	ni		F(t)
1	2	3	4	5	6	7	8	9	10
1	0	0	1	0,0130	-	-	-	-	0
2	10	0,13	0,878	0,0114	0,122	12,2	15	0,643	0,122
3	20	0,26	0,770	0,0100	0,108	10,8	14	0,948	0,230
4	30	0,39	0,677	0,0088	0,093	9,3	11	0,311	0,323
5	50	0,65	0,522	0,0068	0,155	15,5	15	0,016	0,478
6	80	1,04	0,353	0,0046	0,169	16,9	14	0,500	0,647
7	110	1,43	0,239	0,0031	0,114	11,4	7	1,700	0,761
8	150	1,95	0,142	0,0018	0,097	9,7	8	0,298	0,858
9	190	2,47	0,085	0,0011	0,037	3,7	5	0,457	0,915
10	250	3,25	0,039	0,0005	0,046	4,6	6	0,426	0,961
11	370	4,81	0,008	0,0001	0,031	3,1	5	1,160	0,992
							100	 = 6,463

Вколонке5 приведены результаты расчета значений плотности вероятности ƒ(t)на границах интервалов, полученные по формуле (8) с использованием функции (е^{- ·t})_i(таблица 3, колонка 4).

На гистограмме (рисунок 1) построена выравнивающая кривая распределения, представляющая собой график функции ƒ(t), которая, сохраняя в основном существенные особенности статистического распределения, свободна от случайных неправильностей хода гистограммы.

При подборе теоретической кривой распределения между ней и статистическим распределением неизбежны некоторые расхождения. Они могут объясняться случайными обстоятельствами, связанными с ограниченным числом опытных данных, или являться существенными - связанными с тем, что подобранная кривая плохо выравнивает данные распределения.

Установить это можно с помощью критерия согласия Пирсона ²

²= , (9)

где k- число интервалов статистического распределения, в примере k=10;

n_i-количество значений случайной величины в каждом интервале (см. таблицу 2, колонка 4);

п-общее число наблюдаемых значений случайной величины, в примере

п = 100;

- теоретическая вероятность попадания случайной величины в i-й интервал (таблица 3, колонка 6).
В колонке 6 таблицы 3 приведены значения вероятностей попадания случайной величины в i-й интервал . Они численно равны приращению функции распределения на интервале (от предыдущих значений колонки 4 вычитаем текущее значение)

или


=[(е^{- ·t})_i–1]–[(е^{- ·t})_i].

) (10)

Вколонке7 рассчитаны значения п· , где n = 100.
Вколонке8 - количество значений случайной величины, попавших в интервал, т. е. абсолютная частота n_i (из колонки 4 таблицы 2).
В колонке 9, так как для интервала 0-10 абсолютная частота n_i= 15 (см. таблицу 3, колонка 4), а значение nP´(t_i)=12,2 (см. таблицу 3, колонка 7), то распределение

²= [n_i–nP´(t_i)]²/nP´(t_i)= (15 - 12,2)² / 12,2 = 0,643.

и так далее проводим расчет в колонке 9.
Распределение ²зависит от параметра R, называемого числом «степеней свободы». Число «степеней свободы» R равно числу интервалов k за вычетом числа независимых условий (связей) S,наложенных на частоты n_i /n

R= k- S. (11)

Число связей S для экспоненциального закона распределения случайной величины S =2,для нормальногоS =3.

По специальной таблице (приложение Б), можно для полученного значения ²и определенного числа «степеней свободы» R найти Р - вероятность того, что величина, распределенная по закону ²,превзойдет это значение.

При этом, если получаемая вероятность Р больше 0,3 - 0,4, обычно признают, что экспериментальные данные не противоречат принятому теоретическому закону распределения случайной величины.

В примере ²=6,463 (колонка 9 таблицы 3) и число степеней свободы

R=10 - 2 = 8.

По таблице в приложении Б для значений ²=6,463 и R=8 находим