ОТН - ПР 3 Мат. обраб. Эспон. законе. Учебнометодическое пособие для выполнения практических работ по дисциплинам Основы надежности

• Название: Учебнометодическое пособие для выполнения практических работ по дисциплинам Основы надежности
• Дата: 13.11.2022
• Размер: 109.58 Kb.
• Имя файла: ОТН - ПР 3 Мат. обраб. Эспон. законе.docx
• Тип: Учебно-методическое пособие; #786773
• страница: 5 из 19

P=0,6.

К наиболее часто употребляемым критериям согласия наряду с критерием

«хи-квадрат» относится также критерий Колмогорова D.

B качестве меры расхождения между теоретическим и статистическим распределениями Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F*(t)и соответствующей теоретической функцией распределения F(t)
D=max|F*(t)–F(t)|. (12)
Величина Dнаходится из графиков F*(t)и F(t).

Нарисунке2 приведены графики статистической и теоретической (экспоненциальной) функций распределения для рассматриваемого примера. Для построения интегральной статистической функции распределения F*(t)используется накопленная частота n_i/n(cм. таблицу 2,

колонка 8).

Вколонке10 таблицы 3 для построения теоретической функции распределения F(t) (экспоненциальной) воспользуемся выражением для этой функции по данным таблицы 3, колонки 4

F(t) =1– е^-·t=1–e^-0,013·t.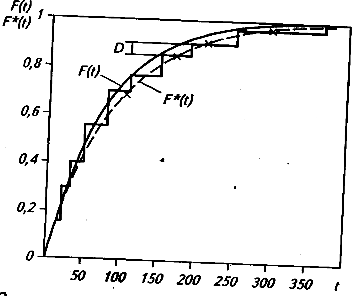



Рисунок 2 - Графики статистической F*(t)и теоретической F(t)

функций распределения
Из рисунка 2 и из сравнения данных колонки 8 таблицы 2 и колонки 10 таблицы 3:
D=|F*(10) – F(10)| = |0,15 – 0,122| = 0,028;

D=|F*(20) – F(20)| = |0,29 – 0,230| = 0,060;

D=|F*(30) – F(30)| = |0,40 – 0,323| = 0,077 = D_max;D=|F*(50) – F(50)| = |0,55 – 0,478| = 0,072;

D=|F*(80) – F(80)| = |0,69 – 0,647| = 0,043; D=| F*(110) – F(110)| = |0,76 – 0,761| = 0,001; D=| F*(150) – F(150)| = |0,84 – 0,858| = 0,018; D=| F*(190) – F(190)| = |0,89 – 0,915| = 0,025; D=| F*(250) – F(250)| = |0,95 – 0,961| = 0,011; D= |F*(370) – F(370)| = |1,00 – 0,992| = 0,008, –
видно, что максимальная разница значений F*(t_i) и F(t_i) наблюдается

при t_i=30 ч. При этом критерий Колмагорова D_maxсоставляет 0,077.
Далее определяется величина
*=D ,

^{* = 0,077· = 0,77.}

По приложению В находится вероятность Р(*)

Р(*)=Р(0,77) = 0,544.

Вывод. Вероятность Р(*) = 0,544 не является малой, таким образом, гипотеза об экспоненциальном законе распределения времени безотказной работы насоса подтверждается также и критерием Колмогорова.