м-ка. Учебнометодическое пособие по проведению лабораторных работ по дисциплине Геодезия для направления подготовки
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
 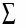  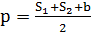 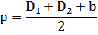         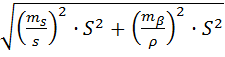 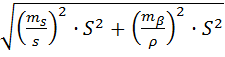  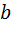 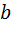 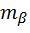 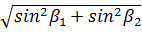 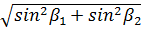 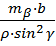 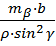 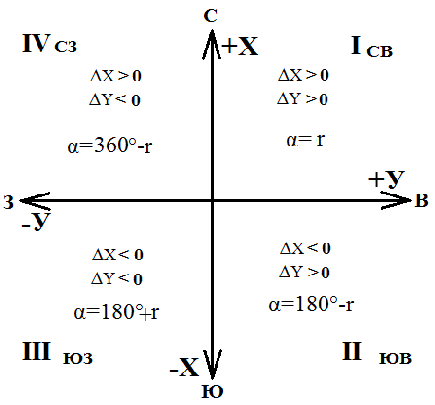 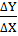 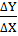 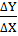 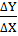 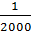 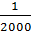 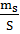 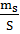       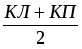    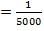 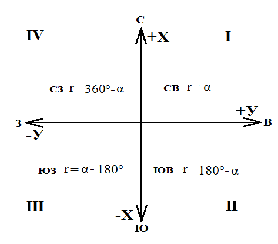  МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Автомобильные дороги и технология строительного производства» Учебно-методическое пособие по проведению лабораторных работ по дисциплине «Геодезия» для направления подготовки 08.03.01 «Строительство» Уфа Издательство УГНТУ 2016 Пособие предназначено для использования студентами по направлению 08.03.01 «Строительство» для выполнения практических работ. В пособии излагаются основные положения по выполнению расчетно-графических работ. Составители: Ромашенко А.А., ст. преподаватель Фаттахова А. М., ст. преподаватель, канд. техн. наук Хакимова Г.Ф., ассистент Рецензент Фаттахов М.М., проф., д-р техн. наук © ФГБОУ ВПО «Уфимский государственный нефтяной технический университет» ОГЛАВЛЕНИЕ
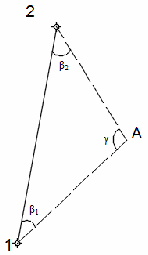
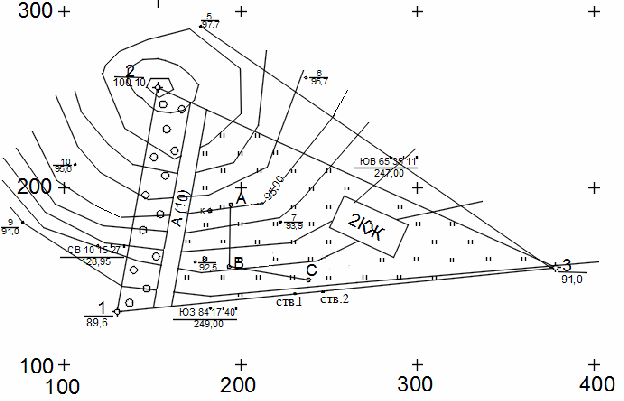
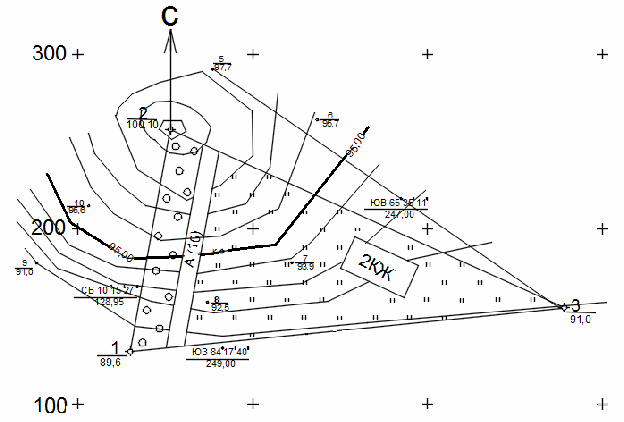
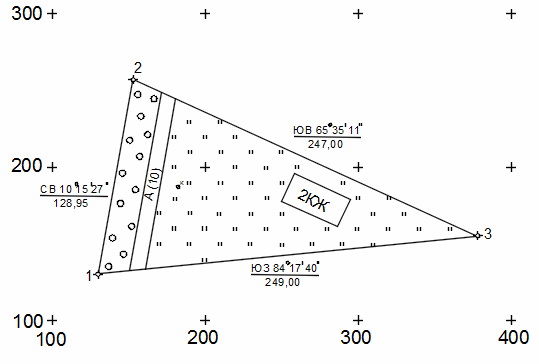
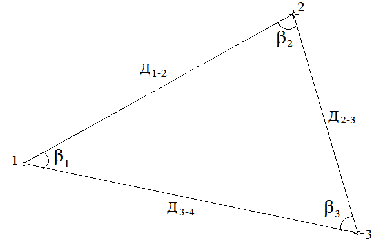
ВВЕДЕНИЕ 1. ПОСТРОЕНИЕ ТОПОГРАФИЧЕСКОГО ПЛАНА УЧАСТКА. 1.1 Теодолитная съемка Геодезические работы, как правило, имеют два этапа: полевые работы (измерения на местности) и камеральные работы (обработка результатов полевых измерений) и составление чертежей. При выполнении РГР студентам предлагается выполнить второй этап работ – камеральные работы по готовым данным полевых измерений. На местности проложен теодолитно-нивелирный ход, показанный на рис. 1. Координаты первой точки теодолитного хода известны – X1 и Y1, а также дирекционный угол первой стороны теодолитного хода 1-2 – α1-2. Внутри контура измерены правые по ходу горизонтальные углы с помощью электронного теодолита VEGA TEO-20 с точностью ±20''. Измерены длины линий с помощью 50-м рулетки с точностью ±1/2000. Измеренные углы и длины линий представлены в табл. 1. Таблица 1 Ведомость измеренных углов и длин линий
Рис. 1.Замкнутый теодолитный ход Необходимо определить координаты точек теодолитного хода и построить контурный план местности. Координаты вершин теодолитного хода определяются путем решения прямой геодезической задачи, сущность которой была рассмотрена в лекционном материале. Работа начинается с заполнения графы 1 табл. 2 «Ведомости вычисления координат теодолитного хода». Номера вершин теодолитного хода удобно записывать через строчку, чтобы между ними заносить данные для сторон теодолитного хода. В графу 2 против номеров вершин вносят результаты измерения горизонтальных углов из табл. 1. В графу 6 вносят длины сторон теодолитного хода из табл. 1 соответственно. 1.1.1 Обработка результатов теодолитной съемки Последовательность обработки данных измерений следующая 1. Вычисляется сумма измеренных углов по всему ходу Σβизм.= β1 + β2 + β3, где β1,β2,β3 – измеренные углы. Σβизм.= β1=74˚02'13''+75˚50'40''+30˚07'10''=180˚00'03'' 2. Вычисляется сумма теоретических сумма углов для замкнутого теодолитного хода Σ βтеор.=180∙(n-2), где n – число вершин замкнутого теодолитного хода. Σ βтеор.=180∙(3-2)= 180˚00'00'' 3. Вычисляется практическая угловая невязка теодолитного хода (fβ) fβ= Σβизм.- Σ βтеор. fβ=180˚00'03''-180˚00'00''=+00˚00'03'' 4. Вычисляется максимально допустимая угловая невязка (fβдоп.) fβдоп.=±2∙t· 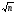 где t – точность теодолита. fβдоп.=±2∙20''∙ 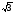 =±69''=±00˚01'09'' =±69''=±00˚01'09''5. Если практическая угловая невязка fβ не превышает fβдоп., то она распределяется равномерно по измеренным углам с противоположным знаком путем введения поправки V и получаем исправленные углы βиспр. V= - 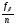 , ,βиспр.= βизм.+ V, V=- 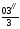 = -01''. = -01''.Значение исправленных углов теодолитного хода вносятся в графу 3 табл. 2. 6. Выполняется контроль: сумма исправленных углов в замкнутом теодолитном ходе должна быть равна Σ βтеор. Σ βиспр.= Σ βтеор.= 180˚00'00'' Полученные суммы и величины из п. 1-6 обработки необходимо внести в ведомость подсчета вершин теодолитного хода через две строки после последней вершины (3) в соответствующие графы табл. 2. 7. Вычисляются дирекционные углы сторон теодолитного хода. Дирекционный угол α1-2 выдается преподавателем каждому студенту индивидуально. Остальные углы вычисляются по формулам: α2-3= α1-2+180˚- β2.исправ, α3-1=α2-3+180˚- β3.исправ. Если вычисленный дирекционный угол получается больше 360˚, то необходимо вычесть из него 360˚ и в дальнейшие вычисления подставлять уменьшенный угол. 8. Выполняется проверка Α1-2= α3-1+180˚- β1.исправ. 9. Вычисляются румбы сторон теодолитного хода по схеме: Рис. 2. Схема вычисления дирекционных углов и румбов сторон теодолитного хода 10. Вычисляется периметр теодолитного хода P=D1-2+ D2-3+ D3-1 где D- длина стороны теодолитного хода. P= 128,95+247,00+249,00=624,95 м. Его необходимо записать в ведомость через 2 строки в графу 6. 11. Вычисляются приращения координат по осям ΔX и ΔY: ΔX=D∙cos α, ΔY= D∙sin α, ΔX1-2= D1-2∙cos α1-2, ΔY1-2= D1-2∙sin α1-2, ΔX2-3= D2-3∙cos α2-3, ΔY2-3= D2-3∙sin α2-3, ΔX3-1= D3-1∙cos α3-1, ΔY3-1= D3-1∙sin α3-1. 12. Вычисляется сумма приращений координат Σ ΔX= ΔX1-2 +ΔX2-3 +ΔX3-1, Σ ΔY= ΔY1-2 +ΔY2-3 +ΔY3-1. 13. Теоретическая сумма приращений координат для замкнутого теодолитного хода должна равняться нулю Σ ΔXтеор.= 0, Σ ΔYтеор.= 0. 14. Вычисляется практическая линейная невязка теодолитного хода по осям ОХ и ОY: fΔХ= Σ ΔX – Σ ΔXтеор, fΔY= Σ ΔY – Σ ΔYтеор. 15. Вычисляется абсолютная линейная невязка: fАБС.= 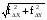 16. Вычисляется относительная линейная невязка, причем она не должна превышать 1/2000 (для данных условий съемочных работ): fОТН.= 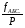 >1/2000 >1/200017. Если выполняется условие пункта 16, то практическая линейная невязка распределяется по приращениям координат с противоположным знаком пропорционально длине стороны теодолитного хода. Для этого подсчитывается поправки по осям ОХ и ОY – VΔX и VΔY: VΔX= - 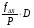 , VΔY= - , VΔY= - 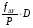 . .18. Вычисляются исправленные приращения координат: ΔX1-2испр.= ΔX1-2+ VΔX1-2, ΔY1-2испр.= ΔY1-2+ VΔY1-2 19. Выполняется контроль: Σ ΔXиспр.= Σ ΔXтеор.= 0, Σ ΔYиспр.= Σ ΔYтеор.= 0. 20. Вычисляются координаты точек теодолитного хода. Координаты первой точки теодолитного хода известны и выдаются преподавателем. Координаты остальных точек вычисляются по формулам: X2=X1+ ΔX1-2испр. , Y2=Y1+ ΔY1-2испр., X3=X2+ ΔX2-3испр. , Y3=Y2+ ΔY2-3испр.. 21. Выполняется контроль: X1=X3+ ΔX3-1испр. Y1=Y3+ ΔY3-1испр. Все полученные результаты вычислений заносятся в ведомость вычисления координат вершин теодолитного хода (табл. 2). Таблица 2 Ведомость вычисления координат вершин теодолитного хода
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 1/5000≤1/2000
1/5000≤1/2000