Поднятие скорости вычисления. Учебнометодическое пособие Разработка письменных рекомендаций по отработке вычислительных навыков (скоростное вычисление) учащихся 4 класса
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
|
Муниципальное образовательное учреждение « Средняя общеобразовательная школа №13» г. Воркуты Учебно-методическое пособие Разработка письменных рекомендаций по отработке вычислительных навыков (скоростное вычисление) учащихся 4 класса. Разработал учитель математики Бабенко Наталия Еманоиловна Воркута 2018 Содержание. 1. Введение. 2. Понятие «вычислительный навык», этапы его формирования. 3. Способы быстрого вычисления чисел. 4. Устный счет - неотъемлемая часть каждого урока математики в школе. 5. Задания, направленные на формирование вычислительных навыков в начальной школе. 5.1 Таблицы, для отработке устного счета. 5.2 Использование нестандартных логических задач . 5.3 Игровые технологии 6. Контрольно-измерительные материалы для проведения проверки сформированности вычислительных навыков в 4 классе. 7. Заключение. Список литературы. Введение. Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных навыков, основу которых составляет осознанное и прочное усвоение приемов устных и письменных вычислений. Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин, а также в обыденной повседневной жизни. В век компьютерной грамотности значимость вычислительных навыков, несомненно, уменьшилась. Использование компьютера, калькулятора во многом облегчает процесс вычислений. Но пользоваться техникой без осознания вычислительных навыков невозможно, да и микрокалькулятор не всегда может оказаться под рукой. Следовательно, владение вычислительными навыками необходимо. Научиться быстро и правильно выполнять вычисления важно для младших школьников как в плане продолжающейся работы с числами, так и в плане практической значимости для дальнейшего обучения. Поэтому вооружение учащихся прочными вычислительными навыками продолжает оставаться серьезной педагогической проблемой. Проблема формирования у учащихся вычислительных умений и навыков всегда привлекала особое внимание. Понятие «вычислительный навык», этапы его формирования. Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе. Эти навыки должны формироваться осознанно и прочно, так как на их базе строится весь начальный курс обучения математике, который предусматривает формирование вычислительных навыков на основе сознательного использования приемов вычислений. Вычислительные навыки рассматриваются как один из видов учебных навыков, функционирующих и формирующихся в процессе обучения. Они входят в структуру учебно-познавательной деятельности и существуют в учебных действиях, которые выполняются посредством определенной системы операций. Полноценный вычислительный навык учащихся, характеризуется следующими показателями: правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом и прочностью. Правильность – ученик правильно находит результат арифметического действия над данными числами, т.е. правильно выбирает и выполняет операции, составляющие прием. Осознанность – ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это для ученика своего рода доказательство правильности выбора системы операции. Осознанность проявляется в том, что ученик в любой момент может объяснить, как он решал пример и почему можно так решать. Рациональность – ученик выбирает для данного случая более рациональный прием, т. е. выбирает те из возможных операций, выполнение которых легче других и быстрее приводит к результату арифметического действия. Это качество навыка может проявляться тогда, когда для данного случая существуют различные приемы нахождения результата, и ученик, используя различные знания, может сконструировать несколько приемов и выбрать более рациональный. Обобщенность –ученик может применить прием вычисления к большему числу случаев, т. е. он способен перенести прием вычисления на новые случаи. Автоматизм (свернутость) – ученик выделяет и выполняет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операции. Осознанность и автоматизм вычислительных навыков не являются противоречивыми качествами. Они всегда выступают в единстве: при свернутом выполнении операции осознанность сохраняется, но обоснование выбора системы операции происходит свернуто в плане внутренней речи. Прочность – ученик сохраняет сформированные вычислительные навыки на длительное время. О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции приводящие к решению. Сознательное использование приемов становится возможным благодаря тому, что в программу начальной школы включено знакомство с некоторыми важнейшими свойствами арифметических действий и вытекающими из них следствиями. Существует 2 подхода к методике формирования вычислительных умений и навыков. 1 подход (традиционный/ объяснительно-иллюстративный) – показ образца способа действия (вычислительного приема) для частных случаев, который чаще всего разъясняется на предметном уровне. Нахождение результата выражения закрепляется в процессе выполнения тренировочных упражнений (с проговариванием вслух, затем про себя), результатом которых является поэтапный выработок навыка. При таком подходе основные усилия учеников сосредоточены на восприятии готовых знаний, их закреплении и воспроизведении. В результате такой репродуктивной деятельности вырабатывается запланированный навык, при этом дети часто не осознают, на основе каких знаний выбраны операции и установлен порядок их выполнения. I. Подготовка к введению нового приема: учащиеся должны усвоить те теоретические положения, на которых основывается приём вычислений, овладеть каждой операцией, составляющей прием; II. Ознакомление с вычислительным приёмом: ученики усваивают суть приёма (какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия). При введении большинства вычислительных приёмов важно использовать наглядность (оперирование множествами, развернутая запись), выполнение каждой операции важно сопровождать пояснениями вспух (сначала эти пояснения выполняется под руководством учителя); III. Закрепление знания приёма и выработка вычислительного навыка: ученики должны твердо усвоить систему операций, составляющую приём, и быстро выполнить эти операции. 2 подход (развивающий) – учащиеся в основном выполняют не воспроизводящую, а преобразующую деятельность (самостоятельно добывают и при необходимости перестраивают ранее полученные знания). Такой подход ориентирован на открытие и усвоение общего способа действий младшими школьниками, в основе которого лежит осознание детьми записи чисел в десятичной системе счисления и смысла арифметических действий. Выполнение школьниками действий с моделями десятков и единиц и соотнесение этих действий с математической записью, наблюдение и анализ специально подобранных выражений, выявление в них сходства и различия позволит показать те или иные предположения о возможном способе действия (вычислительном приеме). В системе развивающего обучения, независимо от пути, формирование вычислительных навыков проходит следующие этапы: I. осознание основных положений, лежащих в основе выполнения операции и создание алгоритма выполнения операций (устные рассуждения детей переводятся в запись математическими знаками, создается подробная запись выполнения операций); II. формирование правильного выполнения операций (ученикам даются такие задания, которые ставят детей в позицию активного творческого поиска: к чему приведет то или иное изменение компонентов операции); III. достижение высокого темпа выполнения операций (проявление интереса к вычислениям учащимися). Чтобы навыки вычислений постоянно совершенствовались, необходимо установить правильное соотношение в применении устных и письменных приёмов вычислений, а именно: вычислять письменно только тогда, когда устно вычислять трудно. Цель устных упражнений: активизировать внимание детей на уроках математики, сделать процесс учения более интересным, повышать с помощью них познавательный интерес к уроку математики. Задания в занимательной форме более доступны и привлекательны для детей. Учащиеся незаметно для себя выполняют большее число арифметических действий, упражняются в устных вычислениях. В данной работе рассмотреть приемы быстрого сложение и вычитание, умножения и деления. Часто нам приходится, применяя полученные знания, действовать не только по образцу, но и в нестандартных ситуациях, комбинируя известные способы решения учебной задачи. Самые простые приемы, основанные на свойствах арифметических действий, (переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения) представлены в учебниках математики, но их мы, ученики, часто используем лишь для несложных вычислениях, т.е. применяем лишь в знакомой ситуации. Вычислительное умение предполагает усвоение вычислительного приема. Любой вычислительный прием можно представить в виде последовательности операций, выполнение каждой из которых связано с определенным математическим понятием или свойством. 3. Способы быстрого вычисления чисел. 3.1 Способы быстрого сложения чисел. Поразрядное сложение двузначных чисел К разрядам первого слагаемого прибавляют разряды второго слагаемого, начиная с высших (сотни, десятки и т.д.). 76 + 38 + 47 + 86 + 45 = (70 + 30 + 40 + 80 + 40) +(6 + 8 + 7 + 6 + 5) = 260 + 32= 292. Сложение путем последовательного прибавления к одному числу отдельных разрядов другого числа, всегда начиная с высших. К разрядам первого слагаемого прибавляют разряды другого слагаемого. 56 + 47 = (56 + 40) + 7 = 96 + 7 = 103; 8375 + 473 = ((8375 + 400) + 70) + 3 = (8775 + 70) + 3 = 8845 + 3 = 8848. Сложение путем округления Если слагаемые близки к круглым числам, то их заменяют разностью или суммой между круглым числом и дополнением. 3916+991+1998+2002=(4000+1000+2000+2000)–(84+9+2)+2=9000–95+2=8907. Сложение с использованием свойств действий с числами Слагаемые разбивают на такие группы, которые в сумме дают круглые числа 12 + 63 + 28 = (12 + 28) + 63 = 40 + 63 = 103; 3013 + 74 + 2187 + 126 = (3013 + 2187) + (74 + 126) =5200 + 200 = 5400. Прибавляют к какому-нибудь числу сумму чисел; можно прибавлять к данному числу каждое слагаемое отдельно 863 + (346 + 137) = 863 + 346 + 137 = 863 +137+ 346 = 1000 + 346 = 1346. Если одно слагаемое близко к круглому числу, то его заменяют разностью и дополнением между круглым числом 549 + 94 = 549 + (100 – 6) = 549 + 100 – 6 = 643. Если оба слагаемых близки к круглому числу, то они заменяются разностью между круглым числом и дополнением 298 + 397 = 300 – 2 + 400 – 3 = 700 – 5 = 695; 504 + 497 = 500 + 4 + 500 – 3 = 1001. 3.1 Способы быстрого вычитания чисел. Поразрядное вычитание 574 - 243 = (500 - 200) + (70 - 40) + (4 - 3) = 300 + 30 + 1= 331. Если число единиц какого-либо разряда вычитаемого больше числа единиц того же разряда уменьшаемого, то последнее число единиц увеличивается на 10 путем заимствования одной единицы следующего высшего разряда уменьшаемого. 647 – 256 = (500 - 200) + ( 140 - 50 ) + ( 7 - 6) = 300 + 90 + 1 = 391. Вычитание с использованием свойств действий с числами 1358 – (158 + 78) = (1358 – 158) – 78 = 1112; (973 +747) - 873 = (973 - 873) + 747 = 100 + 747 = 847; 5861 + (1414 – 884) = (5861 + 1414) - 884 = 7275 - 884 = 6391; 1093 - (1494 - 907) = (1093 + 907) = 2000 - 1494 = 506. Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого 67 - 48 = (67+1) - 48 = (68 - 48) - 1 = 20 - 1 = 19; 453 - 316 = 453 – (313 + 3) = (453 - 313) - 3 = 140 - 3 = 137. Вычитание путем округления уменьшаемого или вычитаемого или одновременно обоих. Если уменьшаемое и/или вычитаемое близки к круглому числу, то их заменяют разностью или суммой между круглым числом и дополнением. 713 - 65 = (700 + 13) - 65 = (700 - 65) + 13 = 635 + 13 = 648; 824 - 396 = 800 – (400 - 4) = (824 - 400) + 4 = 424 + 4 = 428; 395 – 98 = (400 – 5) – (100 – 2) = 400 – 100 – 5 + 2 = 297 3.3 Способы быстрого умножения и деления чисел. Вся современная вычислительная техника работает на принципах табличного умножения, которые придумал древний математик Пифагор. Так как решение многих практических задач с помощью сложения неудобно или невозможно, то нужно использовать готовые значения произведений, которые собраны в таблицу. Но не всем учащимся в силах выучить таблицу умножения и не обязательно зубрить таблицу умножения. Для запоминания существуютразличные способы и приёмы, так называемые «премудрости для забывчивых взрослых и ленивых детей». Умножение и деление на 9  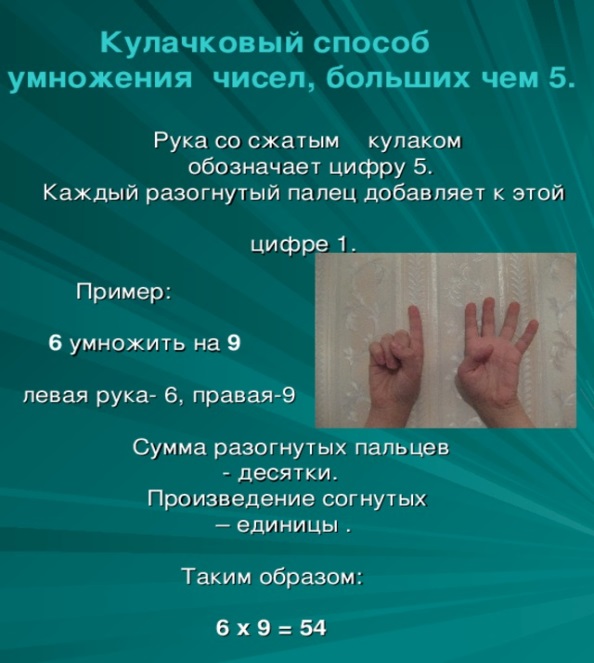 Пальцевый метод Положить обе руки на стол и вытянуть пальцы. Пусть каждый палец по порядку (слева на право) означает соответствующее число от одного до десяти. Например: 6 умножить на 9. Загибаем палец под номером 6 (большой палец) на правой руке. Число десятков произведения равно 5, столько пальцев лежит слева. А число единиц равно 4, столько пальцев справа. Таким образом: 9*6=54. Кулачковый метод Рука со сжатым кулаком обозначает цифру 5. Каждый разогнутый палец добавляет к этой цифре 1.Если сложить количество разогнутых пальцев и перемножить количество согнутых, то получается соответственно числа десятки единиц искомого произведения. 9*6=54 Самый лёгкий способ запоминания таблицы умножения на 9. Число, которое умножаешь, превращаешь в десятки и его же вычитаешь. Например: 9 х 8 = 80 – 8 = 72 данный способ можно использовать и при деление на 9. Например 72: 9 = 80 – 72=8; 63:9=70-63=6; 27:9=30-27=3.   Стихи о таблице умножения. А.Усачёв. Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом.  А Франс А Франс Игра для запоминания таблицы умножения . Каждому ученику выдается листок с записанной на нём таблицей Пифагора, серия примеров и придумывается игровой сюжет. Например: кругосветное путешествие, поиски клада, знакомство с загадочным героем, разгадка тайны, распознай цифру и т.д. На листе записаны примеры и таблица Пифагора. В примерах в виде рисунка зашифрован ключ к разгадке тайны. Необходимо найти результаты произведений и закрасить клетки с ответами. В конце игры на таблице увидите тайное изображение. Первый множитель записан в левом столбике, а 2-й множитель — в верхней строчке. На их пересечении найдите клетку с ответом. Заштрихуйте ее карандашом. Будьте внимательны! В таблице Пифагора многие произведения повторяются дважды, если вы перепутаете место, где записан 1-й и 2-й множители, то можете попасть не в ту клетку, которая вам нужна, и тогда вам не удастся увидеть изображение. Примеры задания.  Умножение на 4,8,16 и т.д. Чтобы число умножить на 4, 8, 16 его последовательно удваивают. 213 Умножение и деление на 5,50,500 и т. д. Умножение на 5,50,500 и т. д. заменяется умножением на 10,100,1000 и т. д. с последующим делением на 2 полученного произведения (или делением на 2 и умножением на 10,100,1000 и т. д.). ( 50 = 100: 2 и т.д.) 54*5=(54*10):2=540:2=270 (54*5 = (54:2)*10= 270). Чтобы число разделить на 5, 50, 500 и т.д, надо это число разделить на 10,100,1000 и т. д. и умножить на 2. 10800 : 50 = 10800:100*2 =21610800 : 50 = 10800*2:100 =2162. Умножение и деление на 25,250,2500 и т. д. Умножение на 25,250,2500 и т. д. заменяется умножением на 100,1000,10000 и т. д. и полученный результат разделить на 4. (25 = 100: 4) 542*25=(542*100):4=13550 (248*25=248: 4*100 = 6200 )(если число делится на 4, то выполнение умножения не занимает времени, любой ученик может выполнить). Чтобы выполнить деление числа на 25, 25,250,2500 и т. д. это число надо разделить на 100,1000,10000 и т.д. и умножить на 4 31200: 25 = 31200:100*4 = 1248 Умножение и деление на 125,1250,12500 и т. д. Умножение на 125,1250 и т. д. заменяется умножением на 1000,10000 и т. д. и полученное произведение нужно делить на 8. (125 = 1000: 8) 72*125=72*1000:8=9000 Если число делится на 8, то сначала выполним деление на 8 , а потом умножение на 1000,10000 ит. д.48*125 = 48:8*1000 = 6000. Чтобы разделить число на 125, 1250 и т.д., надо это число разделить на 1000,10000 и т. д. и умножить на 8. 7000: 125 = 7000:1000*8 = 56. Умножение и деление на 75,750 и т. д. Чтобы число умножить на 75,750и т. д. надо это число разделить на 4 и умножить на 300, 3000 и т.д. (75 = 300: 4) 48* 75 = 48:4*300 = 3600 Чтобы число разделить на 75,750 и т. д. надо это число разделить на 300, 3000 и т.д. и умножить на 4 7200: 75 = 7200: 300*4 = 96.5. Умножение на 15. При умножении на 15, нужно к исходному числу прибавить его половину. 23х15=23х(10+5)=230+115=345; если же число четное, то поступаем еще проще —к числу прибавляем его половину и результат умножаем на 10:18х15=(18+9)х10=27х10=270. При умножении числа на150 пользуемся тем же приемом и умножаем результат на 10, т.к.150=15х10:24х150=((24+12)х10)х10=(36х10)х10=3600.Точно так же быстро умножить двузначное число (особенно четное) на двузначное, оканчивающиеся на 5 24*35 = 24*(30 +5) = 24*30+24:2*10 = 720+120=840.6. Перемножение двузначных чисел, меньших, чем 20. К одному из чисел надо прибавить количество единиц другого, эту сумму умножить на 10 и прибавить к ней произведение единиц данных чисел: 18х16=(18+6)х10+8х6=240+48=288. Описанным способом можно умножать двузначные числа, меньшие 20, а также числа, в которых одинаковое количество десятков: 23х24 = (23+4)х20+4х6=27х20+12=540+12=562. Объяснение:(10+a)*(10+b) = 100 + 10a + 10b + a*b = 10*(10+a+b) + a*b = 10*((10+a)+b) + a*b Умножение двузначного числа на 101. Пожалуй, самое простое правило: припишите ваше число к самому себе и умножение закончено. Пример: 57 * 101 = 5757 57 --> 5757 Объяснение: (10a+b)*101 = 1010a + 101b = 1000a + 100b + 10a + b Аналогично производят умножение трехзначных чисел на 1001, четырехзначных -на 10001 и т.п. Умножение числа на 11 Следует "раздвинуть" цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд. Пример:34 * 11 = 374, так как 3 + 4 = 7, семерку помещаем между тройкой и четверкой 68 * 11 = 748, так как 6 + 8 = 14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой. Объяснение:10a+b -произвольное число, где a -число десятков, b -число единиц. Имеем:(10a+b)*11 = 10a*11 + b*11 = 110a + 11b = 100a + 10a + 10b + b = 100a + 10*(a+b) + b, где мы имеем a сотен, a+b десятков и b единиц. т.е. результат содержит a*(a+1)сотен, два десятка и пять единиц. 43625*11 Составляем произведение: 5 единиц, 5+2=7 десятки, 2+6=8 сотни, 6+3=9 тысячи, 3+4=7 десятки тысяч, 4 сотни тысяч.43625*11=479875. Умножение на 22, 33, ...,99 Чтобы двузначное число умножить 22,33, ...,99, надо этот множитель представить в виде произведения однозначного числа на 11. Выполнить умножение сначала на однозначное число, а потом на 11: 15 *33= 15*3*11=45*11=495. Умножение чисел, близких к 100. При увеличении (уменьшении) одного из множителей на несколько единиц умножаем полученное целое число и прибавленные (отнятые) единицы на другой множитель ииз первого произведения вычитаем второе произведение (полученные произведения складываем)98∙8=(100-2) ∙8=100∙8-2∙8=800-16=784.Данный прием представления одного из сомножителей в виде разности позволяет легко умножать на 9, 99, 999. Для этого достаточно умножить число на 10 (100, 1000) и из полученного целого числа вычесть число, которое умножали: 154х9=154х10-154=1540-154=1386. Но еще проще ознакомить детей с правилом —«чтобы умножить число на 9 (99, 999)достаточно вычесть из этого числа число его десятков (сотен, тысяч), увеличенное на единицу, и к полученной разности приписать дополнение его цифры единиц до 10 (дополнение до 100 (1000) числа, образованного двумя (тремя) последними цифрами этого числа): 154х9=(154-16)х10+(10-4)=138х10+6=1380+6=138614. Я считаю, что вычислительные навыки надо развивать, и это посильно каждому уважающему себя человеку, будь то взрослый или ребенок, независимо от его математических способностей, хотя бы, для того чтобы не стать жертвой обмана в нашем сложном мире. На первый взгляд данные способы вычислений кажутся сложными, но, выполняя их многократно, легко запомнить и использовать при решении. Привычка выполнять подобные вычисления устно формирует устойчивый навык, который не раз сыграет добрую службу при изучении более сложного материала. |
