Учебное пособие для студентов 6 курса медикопрофилактического факультета по дисциплине Эпидемиология, военная эпидемиология
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
1.3.Относительные показатели здоровья населения Как было указано выше, из числа относительных интенсивных показателей, характеризующих здоровье (вернее нездоровье) населения, в гигиенических исследованиях чаще всего применяются такие показатели, как болезненность, заболеваемость, смертность, летальность, рождаемость. Болезненность (распространенность, коэффициент распространенности, пораженность, превалентность) − это показатель, характеризующий состояние здоровья (нездоровья) населения определенной территории в конкретный момент времени. Этот коэффициент показывает, какая часть населения больна тем или иным заболеванием в данный момент времени. При этом не имеет значения, возникла данная патология у человека 20 – 25 лет тому назад или в текущем году. Важно, что в момент проведения исследования он страдает эти заболеванием. Информация для определения болезненности может быть получена из материалов диспансеризации или в результате специально организованного медицинского осмотра. Рассчитывают этот показатель по формуле: КБ = nБ – число лиц в группе, страдающих данным заболеванием в определенный момент времени; N – численность изучаемой группы населения в это же время. Основание 10n выбирают в соответствии с коэффициентом с таким расчетом, чтобы хотя бы одна цифра показателя была представлена целым числом. Для заболеваний, которые встречаются часто, основание может быть равно 100 или 1000, для редких заболеваний – 10000 или 100000. Так, для злокачественных новообразований обычно берут основание 100000. Аналитические возможности показателя болезненности ограничены, поскольку на величину его оказывают влияние несколько факторов: ● продолжительность течения болезни (при непродолжительной болезни показатель болезненности ниже, чем при продолжительной); ● тяжесть заболевания (если от какой-либо болезни умирает большое число людей, показатель болезненности снижается); ● миграционная подвижность населения (приток здоровых лиц и отток больных способствуют снижению показателя болезненности, а приток больных и отток здоровых − повышению); ● улучшение возможностей диагностики (ведет к увеличению показателя); ● внедрение современных методов лечения (приводит к сниже нию показателя). Наряду с распространенностью той или иной болезни (болезненностью), важно знать, с какой скоростью возникают новые случаи изучаемого заболевания. Чтобы оценить частоту возникновения новых случаев заболеваний у населения, проживающего на определенной территории, используют показатель заболеваемости. Заболеваемость (инцидентность, коэффициент заболеваемости) характеризует интенсивность изменений состояния здоровья изучаемой группы населения или, другими словами, скорость перехода членов популяции из категории здоровых в категорию больных. Показатель заболеваемости рассчитывают по формуле: К3 = 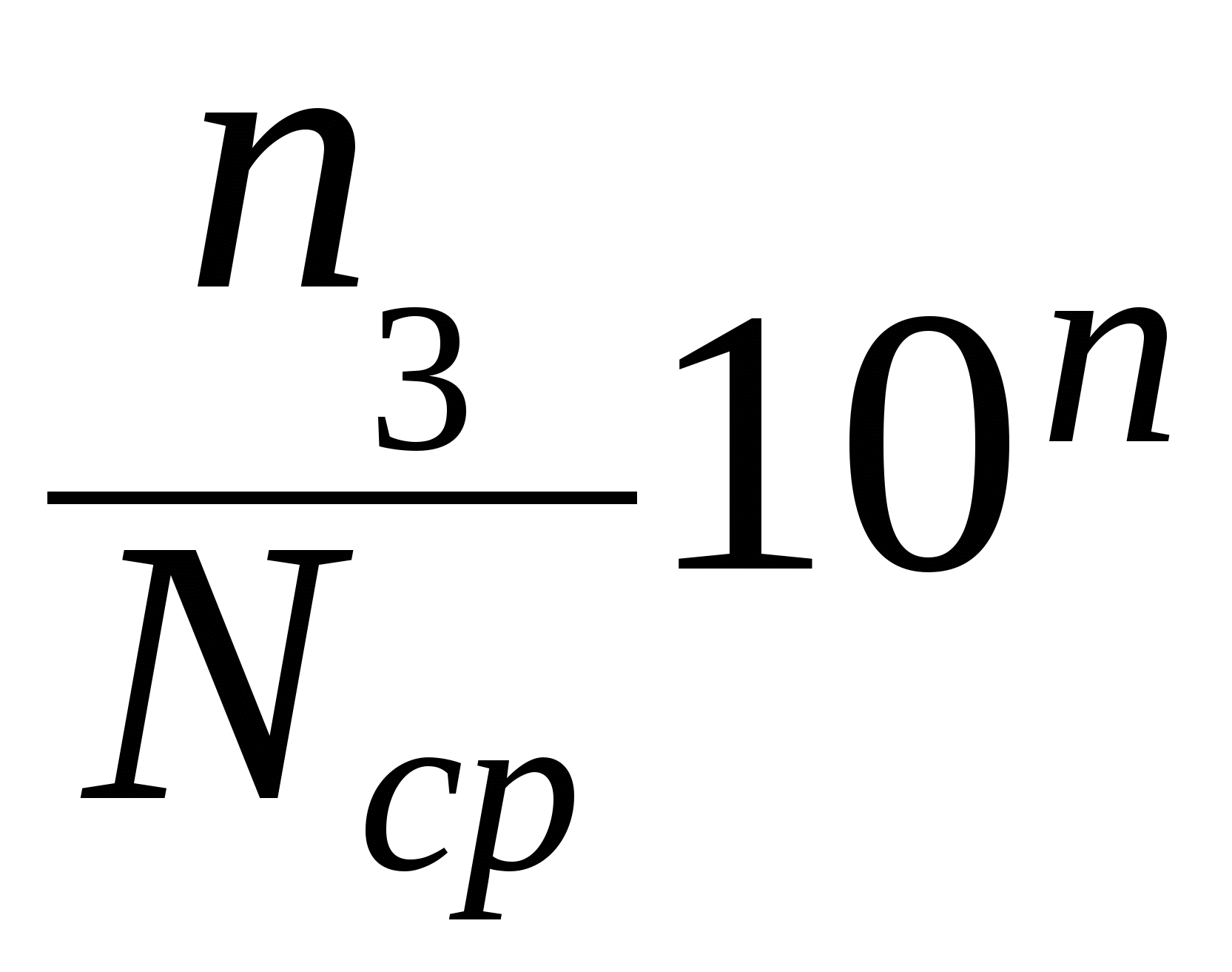 , где , гдеn3 − число заболевших лиц в популяции на протяжении 1 года; Nср. − средняя (за год) численность популяции. Сведения о вновь зарегистрированных случаях заболевания получают из материалов статистической отчетности лечебно-профилактических учреждений, по данным регистров, а также в результате специально организованных исследований. Показатель заболеваемости свободен от действия большинства факторов, оказывающих влияние на распространенность заболеваний (болезненность, превалентность), поэтому он является более информативным при использовании в последующих аналитических исследованиях. Показатели заболеваемости и болезненности в гигиенических исследованиях применяются наиболее часто. Показатели естественного движения населения (смертность, летальность, рождаемость) для характеристики его здоровья используются значительно реже. Смертность − это показатель, отражающий уровень (частоту) смерти от данной болезни среди изучаемого населения за определенный отрезок времени: nc − число умерших от данной болезни за данный отрезок времени; Nср − средняя (за изучаемый отрезок времени) численность населения на данной территории. Показатели смертности отражают очень сложные демографические процессы. На них влияют многие биологические, социальные, медицинские факторы. Выделить среди них действие загрязнения окружающей среды нелегко. Поэтому показатели смертности обычно используют лишь в ориентировочных исследованиях, сравнивая показатели смертности в городах с различной степенью загрязнения окружающей среды. Для таких сравнительных исследований используют показатели смертности от сердечно-сосудистых заболеваний и злокачественных новообразований. К этим показателям прибегают при изучении как хронического, так и острого действия загрязняющих веществ. Острое действие выявляют по изменению числа смертей в дни повышенных уровней загрязнения, хроническое − по динамическим годовым показателям в различных группах населения. Летальность − показатель, отражающий уровень (частоту) смерти от данной болезни среди заболевших данной болезнью: NБ − число болевших данной болезнью. Рождаемость, как изолированный показатель, для оценки воздействия факторов окружающей среды используется редко. Чаще она рассматривается в комплексе показателей, связанных с репродуктивной функцией женщины. Особое значение имеет мертворождаемость, а также рождаемость детей с врожденными аномалиями развития и уродствами, недонашиваемость, поздние аборты (самопроизвольные выкидыши). Перечисленные показатели вычисляют по формулам: np − число детей, родившихся живыми за год, Nср. – средняя (за год) численность населения на данной территории; nм.р. − число детей, родившихся мертвыми, nобщ. − общее число родившихся детей (живыми + мертвыми); nн. − число детей, родившихся недоношенными, nр − число детей, родившихся живыми. Представленные показатели, характеризующие здоровье населения, могут быть общими и специальными. Общие показатели дают обобщенную (интегральную) характеристику явления. Эти показатели называют «грубыми», поскольку они находятся под влиянием состава исследуемых групп населения, в первую очередь по возрасту и полу. Специальные (подгрупповые) показатели применяются для характеристики частоты явления в различных группах (по возрасту, полу и другим признакам). Техника вычисления их та же, что и общих интенсивных показателей. Важно помнить, что для получения интенсивных показателей по возрасту следует число заболевших или умерших в определенном возрасте отнести к численности населения того же возраста. Общие показатели рождаемости, заболеваемости и смертности можно сравнивать между собой только убедившись в том, что возрастно-половая структура сопоставляемых групп не имеет значимых различий. В противном случае необходимо проводить стандартизацию показателей по единому стандарту для элиминирования влияния возрастно-половых различий, которые в данном случае играют роль мешающих факторов. Существуют три метода стандартизации: прямой, косвенный и обратный. Выбор того или иного метода определяется характером данных, которые имеются в распоряжении. Наиболее точным является косвенный метод, а наименее точным − обратный. Обратный метод применяют только в том случае, когда отсутствуют данные о возрастной структуре сравниваемых групп, но есть информация о возрастном составе больных или умерших (Приложение 2). Задания для самостоятельной подготовки к занятиям по теме 1.3 Выберите правильные варианты ответов 1. Из представленных вариантов утверждений верными являются следующие: а) относительные числа служат обобщающей характеристикой качественных признаков объекта; б) относительные числа служат обобщающей характеристикой количественных признаков объекта; в) относительные числа представляют собой соотношение величин; г) относительные числа характеризуют одним числом всю совокупность в целом. 2. Показатели интенсивности характеризуют: а) совокупность в целом; б) распределение целого на части; в) соотношение величин; г) частоту, уровень, распространенность изучаемого явления в среде, которая его продуцирует. 3. Из представленных вариантов утверждений верными являются следующие: а) показатель превалентности показывает, какая часть населе ния больна тем или иным заболеванием в данный момент времени; б) показатель превалентности характеризует интенсивность изменений состояния здоровья изучаемых групп населения; в) смертность – это показатель, отражающий уровень (частоту) смерти от данной болезни среди заболевших данной болезнью; г) смертность это показатель, отражающий уровень (частоту) смерти от данной болезни среди изучаемого населения за определенный отрезок времени. 4. Из представленных вариантов утверждений верными являются следующие: а) показатель «инцидентности» показывает, какая часть населения больна тем или иным заболеванием в данный момент времени; б) показатель «инцидентности» характеризует интенсивность изменений состояния здоровья изучаемых групп населения; в) летальность – это показатель, отражающий уровень (частоту) смерти от данной болезни среди заболевших данной болезнью; г) летальность Сформулируйте ответы на вопросы 1. Дайте определение показателя болезненности. 2. Как рассчитывается показатель болезненности? 3. Дайте определение показателя заболеваемости. 4. Как рассчитывается показатель заболеваемости? 5. Дайте сравнительную характеристику показателей болезненности и заболеваемости. Что влияет на соотношение показателей болезненности и заболеваемости? Приведите примеры. 6. Дайте определение показателя смертности. 7. Как рассчитывается показатель смертности? 8. Дайте определение показателя летальности. 9. Как рассчитывается показатель летальности? 10. Дайте сравнительную характеристику показателей смертнос - ти и летальности. Что влияет на соотношение показателей смертности и летальности? Приведите примеры. 11. В чем состоит различие между общими и специальными ин - тенсивными показателями? Какие из них более достоверно характеризуют состояние здоровья населения? Решите задачи Задача 1 Рассчитайте показатель болезненности рабочих промышленного предприятия болезнями системы кровообращения, если при проведении медицинского осмотра 3268 человек выявлены 557 лиц, больных данной группой заболеваний. Задача 2 Рассчитайте заболеваемость болезнями органов пищеварения населения города N с числом жителей 519,1 тыс. в 2010г., если в течение этого года зарегистрировано 58675 человек, обратившихся за медицинской помощью по поводу заболеваний органов пищеварения. Задача 3 В К-ской области проживает 817,3 тыс. жителей. В 2010г. среди населения области зарегистрировано 184612 случаев острых респираторных инфекций (ОРИ), в том числе гриппа. Умерли от данных болезней 387 человек. Рассчитайте показатели заболеваемости населения ОРИ, смертности от данной группы болезней и летальности при них. Задача 4 В К-ской области проживает 817,3 тыс. жителей. В 2010г. среди населения области зарегистрировано763 случая столбняка. Умерли от данной болезни 372 человека. Рассчитайте показатели заболеваемости населения области столбняком, смертности от данной болезни и летальности при ней. Задача 5 Численность населения N-ской области в 2010г. составляла 1194,8 тыс. Рассчитайте общий показатель и структуру смертности населения области в 2010г., если всего в течение года умерли 24135 человек, из них от: ● инфекционных и паразитарных болезней (кроме туберкулеза) – 24 человека, ● туберкулеза – 217 человек, ● новообразований – 2920 человек, ● болезней эндокринной системы – 145 человек, ● болезней системы кровообращения – 13395 человек, ● болезней органов дыхания – 1062 человека, ● болезней органов пищеварения – 772 человека, ● несчастных случаев, отравлений и травм – 2848 человек, ● других причин – 2752 человек. 1.4. Средние величины В начале раздела 1.2. было указано, что статистические характеристики объекта эпидемиологического исследования могут быть представлены в виде абсолютных чисел или обобщающих величин, к числу которых принадлежат относительные числа (коэффициенты, показатели) и средние величины. Если относительные числа служат обобщающей характеристикой качественных признаков объекта наблюдения, то средние величины выступают в качестве обобщающей характеристики его количественных признаков. В процессе наблюдения за явлением, характеризующимся по количественному признаку, мы получаем отдельные значения признака каждого случая наблюдения − варианты, например, длительность нетрудоспособности каждого больного определенной болезнью, количество эритроцитов в крови каждого обследованного человека, концентрация определенного вещества в каждой пробе определенного объекта окружающей среды, значение физического фактора среды при каждом измерении. Совокупность вариант, расположенных в порядке нарастания их величины, составляет вариационный ряд. Обработка вариационного ряда заключается в выявлении его параметров: средней величины, среднего квадратического отклонения и средней ошибки средней величины. Средняя величина − это величина, характеризующая одним числом всю совокупность в целом. В простом вариационном ряду, где каждая варианта встречается лишь один раз (частоты равны единице), средняя (арифметическая) получается простым суммированием отдельных вариант и делением суммы на их общее число (число наблюдений). В тех рядах, где число наблюдений больше 30, и варианты сгруппированы, вычисляют взвешенную среднюю арифметическую. Формула ее вычисления: хi – значения отдельных вариант, рi– частоты этих вариант. В некоторых случаях средние величины могут быть представлены не в виде средних арифметических, а в форме средних геометрических или средних гармонических. Средняя геометрическая вычисляется тогда, когда изменение членов статистического ряда происходит в соответствии с геометрической прогрессией. Средняя гармоническая вычисляется в том случае, если вариационный ряд представлен дробями, т.е. варианты ряда находятся в знаменателе. В большинстве же случаев под средней величиной понимается именно средняя арифметическая. Средние являются важными характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака, его рассеянности. Естественно, если вариационный ряд более компактен, менее рассеян, и все отдельные значения расположены вокруг средней, то средняя величина лучше характеризует данную совокупность. Если вариационный ряд растянут, отдельные значения признака существенно отклоняются от средней величины, т.е. имеет место большая вариабельность признака, то средняя менее типична, хуже отражает свой ряд. Следовательно, кроме средней величины необходима вторая характеристика ряда – степень его колеблемости. Простейшей мерой рассеянности является вариационный размах – амплитуда колебания, т.е. разность крайних значений ряда (хmax – хmin). Пример 4. При исследовании проб воды в реке (4 раза в месяц в течение 3х летних месяцев) в точке отбора № 1 средняя концентрация хрома равнялась 30 мкг/л, минимальная концентрация составила 24 мкг/л, максимальная концентрация – 37 мкг/л. В точке отбора № 2 средняя концентрация хрома в воде также была равна 30 мкг/л, но минимальная концентрация составила 16 мкг/л, а максимальная – 42 мкг/л. В пробах воды из точки отбора № 1 амплитуда концентраций хрома значительно меньше, и, следовательно, все значения группируются вокруг средней. Вторая совокупность более разнообразна, ее рассеянность велика, отклонения отдельных значений концентраций металла от средней больше. Чаще всего в качестве мерила изменчивости, колеблемости признака используется среднее квадратическое отклонение (δ). Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше. Методика получения среднего квадратического отклонения такова:
арифметической (хi – равняется нулю, то для получения общей величины откло - нений производят дальнейшие вычисления.
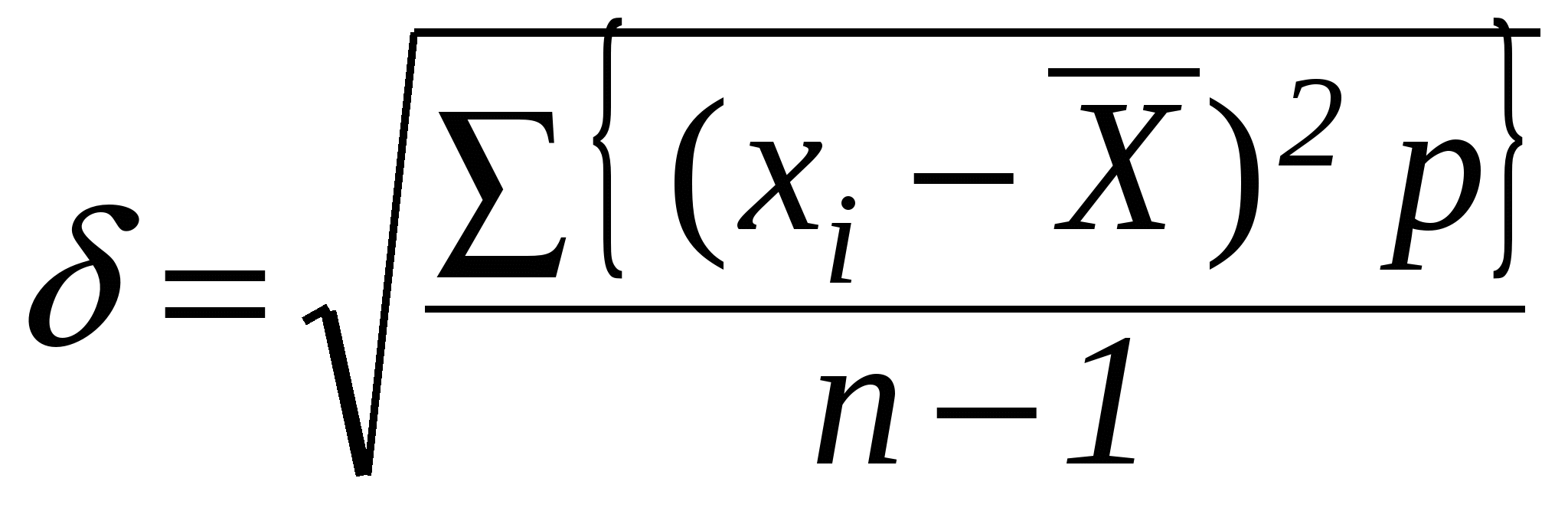 , где , гдеn – число всех вариант. Рассмотрим получение среднего квадратического отклонения на примере 5 (таблица 1). Таблица 1. Температура воды в водоеме в течение июня 2010 года
Вторым возможным вариантом расчета среднего квадратического отклонения может служить приближенный способ вычисления по амплитуде вариационного ряда. Как указывалось выше, амплитудой ряда называется разность между наибольшей и наименьшей вариантами (хmax – хmin). Среднее квадратическое отклонение, исчисленное по амплитуде, несколько отличается от его значения, вычисленного обычным способом. Различие это тем больше, чем больше число наблюдений, использованных для составления вариационного ряда. Поэтому определение среднего квадратического отклонения по амплитуде более целесообразно производить преимущественно при ориентировочных расчетах, а также при небольшом числе наблюдений (менее 30). Вычисление производится по формуле: δ аmpl – амплитуда, k– коэффициент, соответствующий числу наблюдений. Определяется k по специальной вспомогательной таблице (табл.2). В этой таблице числа n в первом вертикальном столбце означают десятки, а в первой горизонтальной строке – единицы наблюдений, например для числа наблюдений 87 (n = 87) k= 4,91, а дляn = 18 k = 3,64. Пример 6. Рассчитаем среднее квадратическое отклонение по амплитуде для вариационного ряда, представленного в табл. 1: δ Для n = 30 k= 4,09 (табл.2), δ Как видим, величина среднего квадратического отклонения, вычисленная по амплитуде, несколько отличается от его значения, полученного при расчете обычным способом, но различие это не слишком велико. Таблица 2. Значения k для вычисления среднего квадратического отклонения (δ) по амплитуде
Задания для самостоятельной подготовки к занятиям по теме 1.4 Выберите правильные варианты ответов 1. Из представленных вариантов утверждений верными являются следующие: а) средние величины служат обобщающей характеристикой качественных признаков объекта; б) средние величины служат обобщающей характеристикой количественных признаков объекта; в) средние величины представляют собой соотношение величин; г) средние величины характеризуют одним числом всю совокупность в целом. 2. Обработка вариационного ряда заключается в выявлении его следующих параметров: а) варианты; б) средняя величина; в) среднее квадратическое отклонение; г) ошибка средней величины. 3. Средняя величина вариационного ряда характеризует: а) совокупность в целом; б) распределение целого на части; в) соотношение величин; г) частоту, уровень, распространенность изучаемого явления в среде, которая его продуцирует. 4. Показателями изменчивости (рассеянности) вариационного ряда являются: а) амплитуда колебания; б) средняя величина; в) среднеквадратическое отклонение; г) средняя ошибка средней величины. Сформулируйте ответы на вопросы
Решите задачу Задача 6 При исследовании 24х проб атмосферного воздуха, отобранных на одном из постов наблюдения в зоне влияния завода по производству электроламповых изделий, концентрации ртути составили: 0,53; 0,54; 0,56; 0,57; 0,57; 0,58; 0,59; 0,61; 0,61; 0,62; 0,63; 0,63; 0,65; 0,65; 0,66; 0,68; 0,69; 0,7; 0,71; 0,72; 0,73; 0,74; 0,74; 0,76 мкг/м3. Рассчитайте среднюю концентрацию ртути в точке наблюдения и ее среднеквадратическое отклонение. 1.5. Оценка достоверности результатов статистического наблюдения В результате статистической обработки материалов исследований получают обобщающие величины, характеризующие совокупность в целом – относительные показатели (коэффициенты) и средние величины. Если эти величины получены на достаточно большом и качественно однородном материале, т.е. если выборка была репрезентативной (представительной), то их можно считать достаточно точными для характеристики изучаемого явления. Получив результат (среднюю величину или показатель), мы считаем его характеристикой изучаемого явления. Точность этой характеристики зависит от числа наблюдений. Чем больше число наблюдений, тем точнее результат. Чем меньше число наблюдений, тем результат хуже отражает изучаемое явление, тем он больше отличается от того результата, который мог бы быть получен на генеральной совокупности (т.е. из всех единиц наблюдения изучаемого явления). Различие результатов выборочного исследования и результатов генеральной совокупности представляет собой ошибку выборочного исследования. Ошибка средней величины или показателя может быть определена математическим путем и оценена. Средняя ошибка показателя рассчитывается по формуле: m– средняя ошибка показателя, p – величина показателя (в долях единицы, процентах или про- милях), q– (1 – p) или (100 –p) или (1000 – p) в зависимости от единиц измерения показателя p, n – число наблюдений. Пример 7. При изучении заболеваемости болезнями щитовидной железы (гипотиреозом) на территории с техногенным загрязнением почвы Ј131 обследовано 400 человек. Гипотиреоз выявлен у 37 человек (9,3 %). Рассчитаем ошибку исследования: m = Средняя ошибка средней рассчитывается по формуле: δ– среднее квадратическое отклонение, n – число наблюдений. |
