Математические методы в географии Учебное пособие - Гриценко В.А., и др.. Математические методы в географии Учебное пособие - Гриценко В. Учебное пособие Калининград 1999

• Название: Учебное пособие Калининград 1999
• Анкор: Математические методы в географии Учебное пособие - Гриценко В.А., и др..doc
• Дата: 29.05.2018
• Размер: 3.78 Mb.
• Имя файла: Математические методы в географии Учебное пособие - Гриценко В.А.doc
• Тип: Учебное пособие; #19766
• Категория: Геология
• страница: 3 из 5

Глава 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Из курса физики хорошо известен принцип сохранения энергии в замкнутой системе. При исследовании природных зависимостей любые изменения энергии системы почти всегда приводят к необходимости вычисления различного рода интегралов от соответствующих функций. Известное из курса математического анализа вычисление определенного интеграла по формуле Ньютона-Лейбница реализовать на практике оказывается не всегда возможно. Например, может случиться, что первообразная F(x) не выражается через элементарные функции или через другие достаточно изученные функции либо выражается слишком сложно. В этих случаях приходится обращаться к методам приближенного интегрирования, т.е. к методам, позволяющим найти численное значение определенного интеграла приближенно с любой степенью точности.
1. Методы численного интегрирования
1.1. Метод прямоугольников
Идея численного интегрирования предельно проста и вытекает из геометрического смысла определенного интеграла – значение определенного интеграла численно равно площади криволинейной трапеции, ограниченной графиком функции y=f(x), осью абсцисс и прямыми х=а, х=b. Находя приближенно площадь криволинейной трапеции, мы получаем значение интеграла. Формально процедура численного интегрирования заключается в том, что отрезок [а, b] разбивается на n частичных отрезков, а затем подынтегральная функция заменяется на нем легко интегрируемой функцией, по определенной зависимости интерполирующей значения подынтегральной функции в точках разбиения. Рассмотрим теперь простейшие из численных методов интегрирования.

Итак, функция у=f(x) интегрируема на сегменте [a,b] и требуется вычислить ее интеграл . Составим интегральную сумму для f(x) на сегменте [a,b]. Для этого разобьем сегмент [a,b] на n равных между собой частей с помощью точек: x₁, x₂, …, x_k, …, x_n-1.

Если длину каждой части мы обозначим через х, так что , то для каждой точки x_k будем иметь: x_k = a + kx (k=0, 1, 2, … n).

Обозначим теперь через y_k значение подынтегральной функции f(x) при x = x_k = a + kx, то есть положим (k=0, 1, … n).

Тогда суммы и будут интегральными для функции f(x) на отрезке [a,b]. (При составлении первой суммы мы рассматриваем значения функции y=f(x) в точках, являющихся левыми концами частичных сегментов, а при составлении второй суммы – в точках, являющихся правыми концами этих сегментов.)

По определению интеграла имеем:



и .

Поэтому в качестве приближенного значения естественно

взять интегральную сумму и , т.е. положить:

,

а также

,

т.е.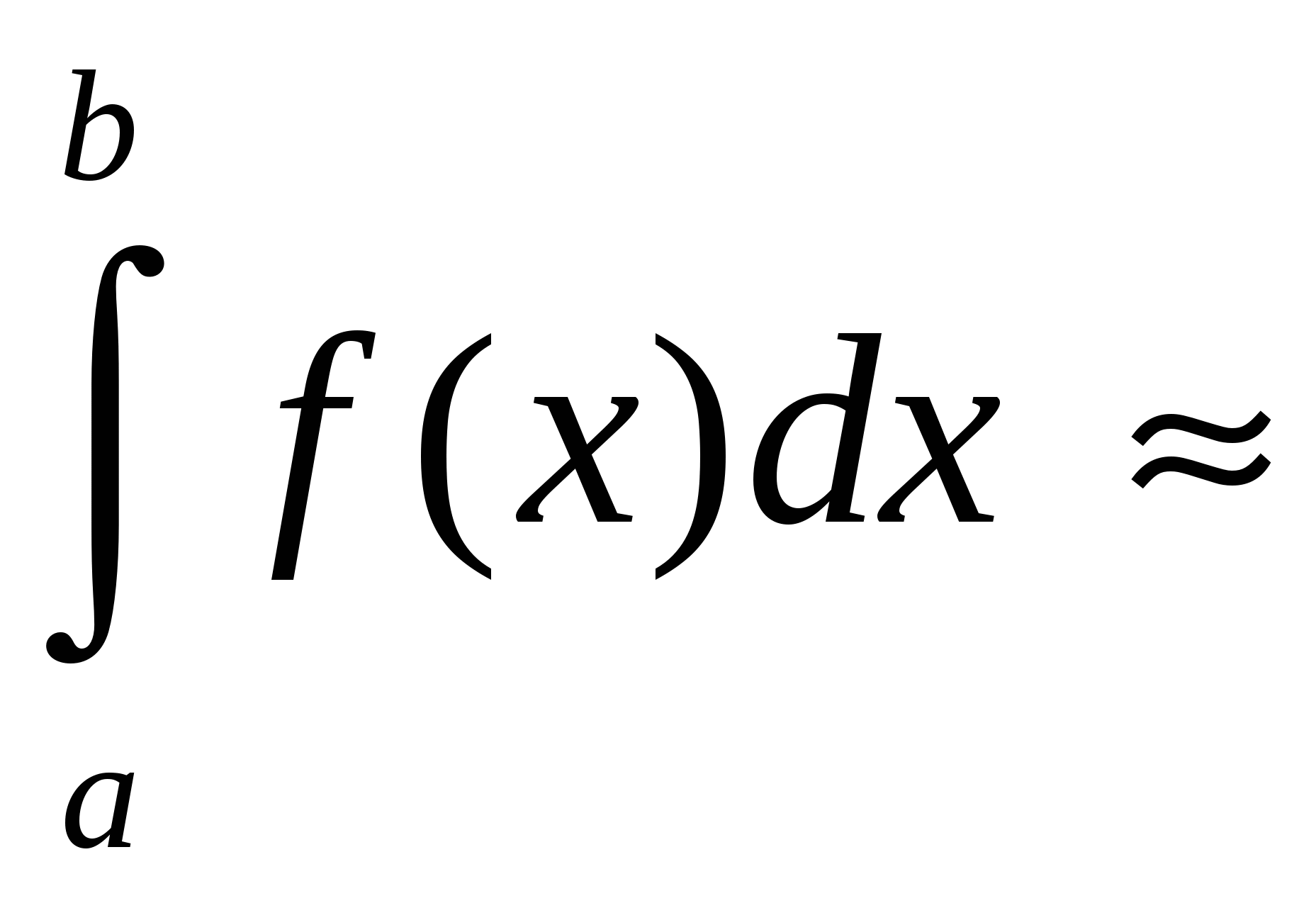

(1)

и



(2)

Эти приближенные равенства называются формулами прямоугольников.

В том случае, когда f(x)0, формулы (1) и (2) с геометрической точки зрения означают, что площадь криволинейной трапеции aABb, ограниченной дугой кривой y=f(x), осью Ох и прямыми х=а и х=b, принимается приближенно равной площади ступенчатой фигуры, образованной из n прямоугольников с основаниями 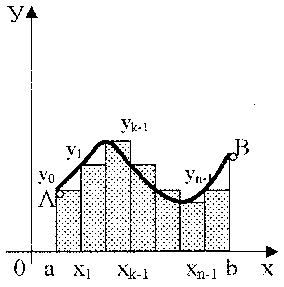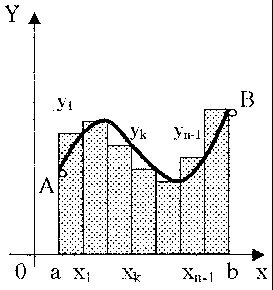и высотами: y₀, y₁, y₂, … y_n-1 – в случае формулы (1) (рис. 8) и y₁, y₂, y₃, … y_n – в случае формулы (2) (рис. 9).

Рис. 8 Рис. 9
Исходя из приведенного выше геометрического смысла формул (1) и (2) способ приближенного вычисления определенного интеграла по этим формулам принято называть методом прямоугольников.

Всякое приближенное вычисление имеет определенную ценность лишь тогда, когда оно сопровождается оценкой допущенной при этом погрешности. Поэтому формулы прямоугольников будут практически пригодны для приближенного вычисления интегралов лишь в том случае, если будет существовать удобный способ оценки получающейся при этом погрешности (при заданном n), позволяющий к тому же находить и число частей n разбиения сегмента, гарантирующее требуемую степень точности приближенного вычисления.

Будем предполагать, что функция f(x) имеет ограниченную производную на сегменте [a, b], так что существует такое число М>0, что для всех значений х из [a, b] выполняется неравенство |f'(x)|  M. Качественный смысл этого неравенства заключается в том, что скорость изменения значения функции ограничена. В реальных природных системах это требование практически всегда выполнено. В этих условиях абсолютная величина погрешности R_n, которую мы допускаем, вычисляя интеграл по формуле прямоугольников, может быть оценена по формуле [27]:

|R_n|  M(b-a)²/2n. (3)

При неограниченном возрастании n выражение M(b-a)²/2n, а следовательно, и абсолютная величина погрешности R_n будет стремиться к нулю, т.е. точность приближения будет тем больше, чем на большее число равных частей будет разделен сегмент [a, b]. Абсолютная погрешность результата будет заведомо меньше заданного числа >0, если взять

n > M(b-a)²/2.

Следовательно, для вычисления интеграла с указанной степенью точности достаточно сегмент [a, b] разбить на число частей, большее числа M(b-a)²/2. [27].

Метод прямоугольников – это наиболее простой и вместе с тем наиболее грубый метод приближенного интегрирования. Заметно меньшую погрешность дает другой метод – метод трапеций.
1.2. Метод трапеций
Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут формулы (1) и (2). Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно. Поэтому большой интерес представляют формулы, дающие более точные результаты при том же числе точек разбиения.

Простейшая из таких формул получается как среднее арифметическое правых частей формул (1) и (2):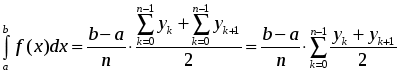

. (4)

Легко усмотреть геометрический смысл этой формулы. Если на каждом отрезке разбиения дугу графика подынтегральной функции y=f(x) заменить стягивающей ее хордой (линейная интерполяция), то мы получим трапецию, площадь которой равна 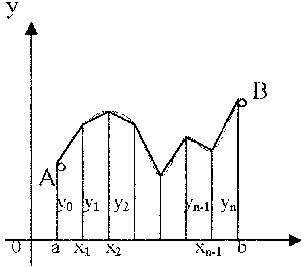и, следовательно, формула (4) представляет собой площадь фигуры, состоящей из таких трапеций (рис. 10). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемой в методе прямоугольников.

Рис. 10
Приведя в формуле (4) подобные члены, окончательно получим

. (5)

Формулу (5) называют формулой трапеций.

Формулой трапеций часто пользуются для практических вычислений. Что касается оценки погрешности R_n, возникающей при замене левой части (5) правой, то доказывается, что абсолютная величина ее удовлетворяет неравенству:

, (6)

где М₂ – максимум модуля второй производной подынтегральной функции на отрезке [a,b], т.е.

.

Следовательно, R_n убывает при n8 по крайней мере так же быстро, как . Абсолютная погрешность R_n будет меньше наперед заданного числа 0, если взять .

1.3. Метод парабол (метод Симпсона)
Значительное повышение точности приближенных формул может быть достигнуто за счет повышения порядка интерполяции. Одним из таких методов приближенного интегрирования является метод парабол. Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает к кривой y=f(x), чем хорда, соединяющая концы дуги этой кривой, и поэтому значения площадей соответствующих элементарных трапеций, ограниченных «сверху» дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y=f(x), чем значения площадей соответствующих прямолинейных трапеций. Сущность метода заключается в следующем. Отрезок [a,b] делится на 2n равных частей. Пусть точки деления будут

х₀=а, x₁, x₂, …x_2n-2, x_2n-1, x_2n=b,

а y₀, y₁, …y_2n – соответствующие значения подынтегральной функции на отрезке [a,b]. Произведем квадратичную интерполяцию данной подынтегральной функции на каждом из отрезков разбиения (заменим дугу графика подынтегральной функции дугой параболы с вертикальной осью) (рис. 11). Приведем без вывода формулу парабол в окончательном виде:

. (7)

Подробный вывод формулы (7) см. в [13].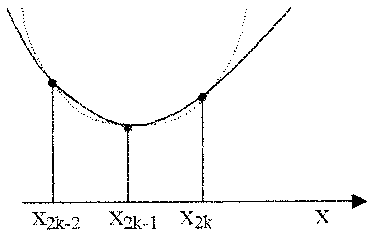

Рис. 11
Если подынтегральная функция f(x) имеет на отрезке [a,b] непрерывную четвертую производную, то для поправочного члена формулы (7) имеет место оценка

, (8)

где М₄ - максимум модуля четвертой производной подынтегральной функции на отрезке [a,b].

Cравнивая между собой оценки (6) и (8), замечаем, что с увеличением n поправочный член формулы трапеций уменьшается пропорционально величине , а для формулы парабол – пропорционально величине , т.е. метод парабол сходится значительно быстрее метода трапеций, тогда как с точки зрения техники вычислений оба метода одинаковы.
ЛАБОРАТОРНАЯ РАБОТА №4
Задание: Вычислить интеграл по формулам левых и правых прямоугольников и по формуле трапеций при n=100. Сравнить полученные результаты со значением интеграла, вычисленным с помощью встроенных функций MathCad.
Образец выполнения задания
f(x) := 2x задание подынтегральной функции

a := 0 b := 1 значения границ отрезка интегрирования

n := 100 число точек разбиения отрезка

величина h – длина отрезка разбиения

вычисление интеграла

i := 0.. n

x_i := ih y_i := f(x _i)

k := 0.. n - 1 p := 1.. n


slev = 0.99 spr = 1.01

t := 0.. n - 1



str = 1
Проверка полученного результата с помощью встроенных функций MathCad для вычисления определенного интеграла: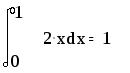







Глава 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Решение большинства задач естествознания после соответствующих упрощений сводится к решению уравнений, содержащих искомую функцию или несколько функций, зависящих от одного или нескольких аргументов, сами эти аргументы и производные различных порядков от искомых функций, так называемых дифференциальных. Дифференциальное уравнение, полученное в результате исследования какого-либо реального процесса или явления, называют дифференциальной моделью этого явления или процесса. Мы будем рассматривать лишь модели, описываемые обыкновенными дифференциальными уравнениями, то есть уравнениями, в которых неизвестные функции зависят только от одной переменной.
1. Постановка задачи Коши
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

y=f(x,y). (1)

Решением дифференциального уравнения является некоторая функция y(x), которая при подстановке в выражение обращает его в тождество. Существует множество решений (так называемых частных решений) дифференциального уравнения (1), которые могут быть объединены и записаны в виде общего решения

y=y(x, C), (2)

где С – произвольная постоянная. Геометрически это можно интерпретировать как семейство интегральных кривых, каждая из которых является графиком решения (1) – рис. 12.

Для выбора одной кривой из семейства (частного решения y=y(x,c)) необходимо задать начальные условия

y(x₀)=y₀, (3)

то есть одну точку на искомой кривой решения.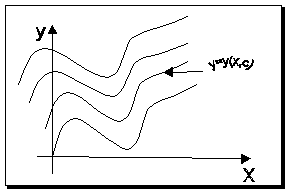




Рис. 12
Как правило, практическое значение всегда имеет частное решение дифференциального уравнения. Задача нахождения частного решения уравнения (1), соответствующего начальным условиям (3), называется задачей Коши.
2. Методы решения обыкновенных дифференциальных уравнений
В классическом анализе разработано немало приемов нахождения решений дифференциальных уравнений через элементарные функции. Между тем при решении практических задач эти методы оказываются, как правило, либо совсем бесполезными, либо их решение связано с недопустимыми затратами усилий и времени. Для решения прикладных задач созданы методы приближенного решения дифференциальных уравнений, которые условно можно подразделить на три основные группы.

1. Аналитические методы, применение которых даст решение дифференциальных уравнений в виде аналитической функции (метод Пикара, [17]).

2. Графические методы, дающие приближенное решение в виде графика (метод Эйлера).

3. Численные методы, когда искомая функция получается в виде таблицы (метод Рунге-Кутта).

Ниже рассматриваются относящиеся к указанным группам некоторые избранные методы решения обыкновенных дифференциальных уравнений первого порядка вида (1). Что же касается дифференциальных уравнений n-го порядка:

y⁽ⁿ⁾ = f(x,y,y,...,y^(n-1)), (4)

для которых задача Коши состоит в нахождении решения y=y(x), удовлетворяющего начальным условиям

, , (5)

где – заданные числа, то их можно свести к системе дифференциальных уравнений первого порядка. Так, например, уравнение второго порядка

, (6)

можно записать в виде системы двух уравнений первого порядка при помощи стандартной замены:

. (7)

Методы решения систем обыкновенных дифференциальных уравнений основываются на соответствующих методах решения одного уравнения (см. [17]).

Очевидно, что ставить вопрос об отыскании приближенных значений интеграла или решения y(x) уравнения (1) можно в том и только в том случае, если решение y(x), удовлетворяющее условию (3), существует и единственно. Как известно из общей теории дифференциальных уравнений, для этого достаточно, чтобы фигурирующая в правой части уравнения (1) функция f(x,y) была непрерывна в рассматриваемой области по обоим аргументам и имела ограниченную частную производную.
3. Метод Эйлера
В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Идея метода заключается в том, что на малом промежутке изменения независимой переменной



интегральная кривая дифференциального уравнения

(8)

заменяется отрезком прямой (касательной)

.

Отсюда и процесс можно повторить для промежутка и т.д. Число h является здесь шагом таблицы. Геометрически интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера (рис.13).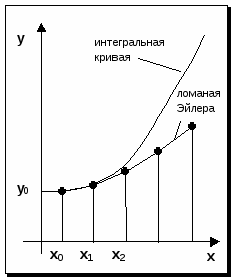




Рис. 13
Рабочая формула для определения значений у по методу Эйлера имеет вид

, (9)

где

, , .

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага, вообще говоря, систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае метод двойного счета – с шагом h и с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными. Ошибка метода пропорциональна h². Существуют различные уточнения метода Эйлера, повышающие его точность так, что ошибка метода становится пропорциональной h³[13].
4. Метод Рунге-Кутта
Пусть дано дифференциальное уравнение первого порядка



с начальными условиями y(x₀)=y₀. Выберем шаг h и для краткости введем обозначения x_i=x₀+ih и y_i=y(x_i), (i=0,1,2,…).

В вычислительной практике наиболее часто используется метод Рунге-Кутта. Приведем без вывода один из вариантов соответствующих расчетных формул: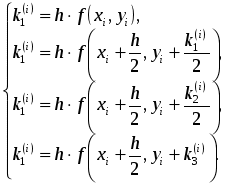

(9)

Последовательные приближения y_i искомой функции y определяются по формуле:

,

где (10)

, (i = 0,1,2,...).

Отметим, что в этом случае погрешность на шаге пропорциональна пятой степени шага (h⁵). Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге-Кутта по формулам (9), будет близким к точному.

Геометрический смысл использования метода Рунге-Кутта с расчетными формулами (9) состоит в следующем. Из точки (x_i,y_i) сдвигаются в направлении, определяемом углом ₁, для которого tg₁=f(x_i,y_i). На этом направлении выбирается точка с координатами (x_i+h/2, y_i+k₁/2). Затем из точки (x_i,y_i) сдвигаются в направлении, определяемом углом ₂, для которого tg₂=f(x_i+h/2, y_i+k₁/2), и на этом направлении выбирается точка с координатами (x_i+h/2, y_i+k₂/2). Наконец, из точки (x_i,y_i) сдвигаются в направлении, определяемом углом ₃, для которого tg₃=f(x_i+h/2, y_i+k₂/2), и на этом направлении выбирается точка с координатами (x_i+h, y_i+k₃). Этим задается еще одно направление, определяемое углом ₄, для которого tg₄=f(x_i+h, y_i+k₃). Четыре полученных направления усредняются в соответствии с последней из формул (9). На этом окончательном направлении и выбирается очередная точка (x_i+1,y_i+1)= (x_i+h,y_i+y).
5.Численное интегрирование систем

обыкновенных дифференциальных уравнений
Метод Рунге-Кутта применяется также для приближенного решения систем обыкновенных дифференциальных уравнений. Пусть, например, дана система дифференциальных уравнений:

, (11)

г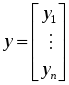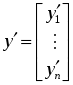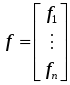де

.

Под решением системы (11) понимается любая совокупность функций (y₁(x), y₂(x),…,y_n(x)), которая, будучи подставлена в уравнения (11), обращает их в тождества. Так как система дифференциальных уравнений имеет бесчисленное множество решений, то для выделения одного конкретного решения кроме уравнения нужны дополнительные условия. В простейшем случае задаются начальные условия

, (12)

что приводит к задаче Коши.

Задача Коши. Найти решение



системы (11), удовлетворяющее заданным начальным условиям (12), где х₀ – фиксированное значение независимой переменной и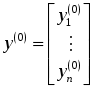



– данная система чисел.

Если х интерпретировать как время, а у₁, … у_n –как обобщенные координаты некоторой механической системы, то получим следующий аспект задачи Коши: зная дифференциальные уравнения, управляющие механической системой, а также состояние ее в начальный момент времени х₀, определить состояние системы в любой момент времени х.

Задавшись некоторым шагом h и введя стандартные обозначения x_i=x₀+ih и y_i=y_i(x),y_i=y_i+1-y_i при i=0,1,2,…, положим: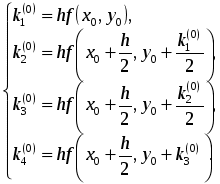

(13)

Согласно методу Рунге-Кутта, y₀ приближенно определяют по формуле

, (14)

отсюда

.

Далее, приняв (x₁,y₁) за исходные данные и повторяя тот же процесс, находим y₂. Аналогично вычисляются

y_i (i=3,4,5,…).

Более подробно с методами решений систем уравнений можно познакомиться в [13].
ЛАБОРАТОРНАЯ РАБОТА №5
Задание: Методом Рунге-Кутта найти решение дифференциального уравнения , удовлетворяющее начальным условиям y(0)=1 на отрезке [0, 8]. Сравнить полученные результаты с решением, полученным с помощью встроенных функций MathCad.
Образец выполнения задания
правая часть дифференциального уравнения

y₀ := 1 x₀ := 0 задание начальных условий

N := 10 число точек разбиения отрезка интегрирования

b := 8 a := 0 границы отрезка интегрирования

вычисление шага интегрирования

h

= 2.513 значение шага интегрирования
расчетные формулы метода Рунге-Кутта, заданные в виде функций пользователя

k1(x, y) := h  f(x, y)








построение точечного решения
i := 0.. (N - 1)

x_i+1 := x_i + h, .
графическое решение уравнения и таблица значений функции у(х)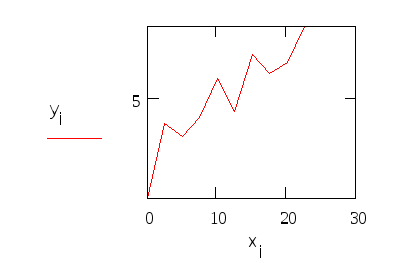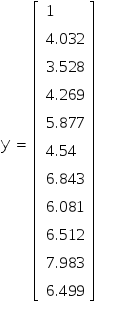

проверка полученного решения с помощью встроенной функции MathCad rkfixed().
правая часть дифференциального уравнения

y₀ := 1 x₀ := 0 задание начальных условий

x1 := 8 конец отрезка интегрирования

N := 10 число точек разбиения отрезка интегрирования

ic₀ := y₀

D(x, Y) := f(x, Y₀)

S := rkfixed(ic, x0, x1, N, D)




X := S^<0>
Y := S^<1>
графическое решение уравнения и таблица значений функции у(х), полученные с помощью встроенных функций MathCad для решения дифференциальных уравнений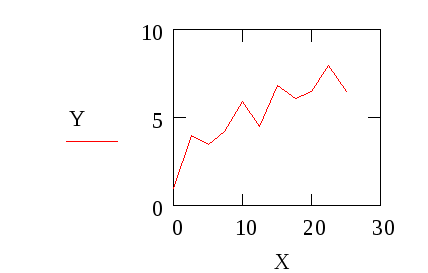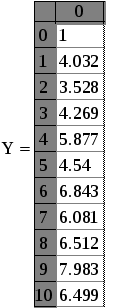


Очевидно абсолютное совпадение полученных решений.

ЛАБОРАТОРНАЯ РАБОТА №6
Задание: Решить методом Рунге-Кутта систему дифференциальных уравнений с данными начальными условиями: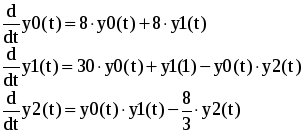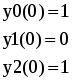



Решение: В пакете MathCad существует несколько встроенных функций для решения систем дифференциальных уравнений. Для решения данной системы мы воспользовались функцией Rkadapt для поиска приближенного решения.

Задавшись фиксированным числом точек, можно аппроксимировать функцию более точно, если вычислять ее значения в точках, расположенных следующим образом: достаточно часто на тех интервалах, где функция меняется быстро, и не очень часто – где функция меняется более медленно. В отличие от функции rkfixed, которая ищет приближенное решение с постоянным шагом, функция Rkadapt проверяет, как быстро меняется приближенное решение, и соответственно адаптирует размер шага. Этот адаптивный контроль величины шага дает возможность функции Rkadapt вычислять решение на более мелкой сетке в тех областях, где оно меняется быстро, и на более крупной – в тех областях, где оно меняется медленно. Это позволяет и повысить точность, и сократить время, требуемое для решения уравнения. Следует обратить внимание на то, что функция Rkadapt возвращает решение системы уравнений на равномерной сетке.

Функция Rkadapt(y,x1,x2,npoints,D) имеет те же самые аргументы, что и функция rkfixed, и возвращает идентичную по виду матрицу с приближенным решением (см. рис.14) [39].