Математические методы в географии Учебное пособие - Гриценко В.А., и др.. Математические методы в географии Учебное пособие - Гриценко В. Учебное пособие Калининград 1999

• Название: Учебное пособие Калининград 1999
• Анкор: Математические методы в географии Учебное пособие - Гриценко В.А., и др..doc
• Дата: 29.05.2018
• Размер: 3.78 Mb.
• Имя файла: Математические методы в географии Учебное пособие - Гриценко В.А.doc
• Тип: Учебное пособие; #19766
• Категория: Геология
• страница: 2 из 5

2. Интерполирование функций
2.1. Постановка задачи интерполяции
Пусть известные значения некоторой функции f образуют следующую таблицу:

х	x0	x1	…	xn
f(x)	y0	y1	…	yn

При этом требуется получить значение функции f для такого значения аргумента х, которое входит в отрезок [x₀;x_n], но не совпадает ни с одним из значений x_i (i=0,1,…,n).

Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках x_i(i=0, 1, 2, …, n), т.е.

F(x₀)=y₀, F(x₁)=y₁, …, F(x_n)=y_n. (1)

В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), а точки x₀, x₁, …, x_n – узлами интерполяции. Геометрически это означает, что нужно найти кривую y=F(x) некоторого определенного типа, проходящую через заданную систему точек M_i(x_i,y_i) (i=0,1,2,…,n) (рис. 1). В случае, если xÏ[x₀, x_n], нахождение искомой функции называют экстраполяцией. В дальнейшем под термином «интерполя­ция» будем понимать как первую, так и вторую операции.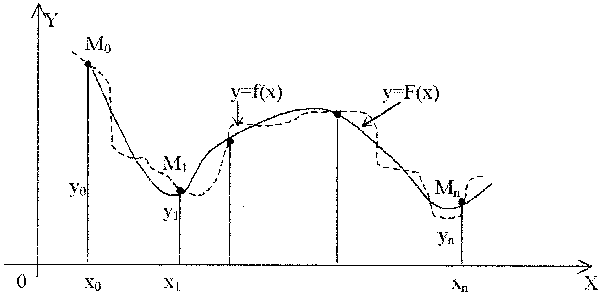

Рис. 1
Задача интерполирования может иметь в общей постановке бесчисленное множество решений или совсем их не иметь. Однако эта задача становится однозначной, если вместо произвольной функции F(x) искать некоторую функцию конкретного вида, удовлетворяющую условиям (1).

Наиболее удобной в практическом использовании функцией является алгебраический многочлен степени n:

P_n(x)=a₀xⁿ + a₁x^n-1 + … + a_n-1x + a_n.

Чтобы задать многочлен n-й степени, достаточно задать его n+1 коэффициент. Значения многочлена просто вычисляются, его легко продифференцировать, проинтегрировать и т.д. Поэтому алгебраические многочлены нашли широкое применение для приближения функций.

Ниже будут подробно изложены широко используемые в географических исследованиях случаи интерполяции линейной функцией (линейная интерполяция) и квадратичной функцией (квадратичная интерполяция). Подробно с методами интерполяции функции полиномами можно познакомиться в [13].

2.2. Линейная интерполяция
Итак, пусть мы имеем функцию, заданную таблично. Решая задачу интерполяции, найдем в таблице два соседних значения аргумента (обозначим их х_k и x_k+1), между которыми лежит заданное значение х (х_k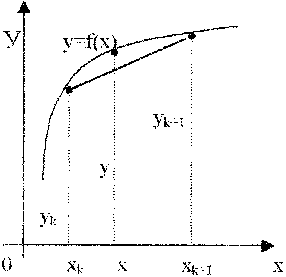k+1), пусть y_k=f(x_k) и y_k+1=f(x_k+1) – соответствующие им значения функции. Будем считать, что в промежутке (х_k, x_k+1) данную функцию с достаточной степенью точности можно заменить линейной функцией, т.е. дугу графика функции можно заменить стягивающей ее хордой (рис.2). Такая замена называется линейной интерполяцией.

Рис. 2
Уравнение прямой, проходящей через точки (х_k, y_k) и (х_k+1, y_k+1), имеет следующий вид:



или в более привычной форме уравнения с угловым коэффициентом:

.

Применение линейной интерполяции для приближенного вычисления значений функции обосновано в том случае, когда возникающая при этом погрешность невелика. Для нахождения погрешности обозначим разность между не известным нам точным значением функции f(x) и ее приближенным значением, определяемым формулой (1) через j(х):

.

Будем предполагать также, что вторая производная функции f(x) на рассматриваемом участке непрерывна и удовлетворяет неравенству

,

где .

Используя аппарат математического анализа, можно доказать [27], что для любого х из интервала (x_k, x_k+1) оценка погрешности линейной интерполяции будет иметь следующий вид:

.

Заметим, что вторая производная функции f(x) имеет конкретный механический смысл. Если f(x) описывает закон движения материальной точки, то вторая производная этой функции задает ускорение этой точки в момент времени х. Факт существования ограничения на ускорение (ограничен­ность второй производной) с физической точки зрения означает, что процесс описываемый функцией f(x), протекает относительно равномерно и функция изменяется не очень быстро. Таковой, например, будет функция, задающая изменение суточной температуры воздуха от времени. На практике именно этим критерием «плавности» скорости изменения процесса вполне можно воспользоваться для ответа на вопрос об обоснованности применения линейной интерполяции.

Окончательно линейная интерполяция считается применимой, если вносимая ею дополнительная погрешность заметно меньше погрешности измерений натурных данных. Если обозначить через m номер последнего разряда приводимых в таблице значений функции, то погрешность измерений будет равна и условие применимости линейной интерполяции запишется в виде неравенства:

. (2)

Шаг и точность таблицы обычно стараются согласовать так, чтобы условие (2) было выполнено.

Бывает, однако, что для выполнения этого условия требуется выбирать слишком малый шаг. В таком случае не считаются с этим условием, а для отыскания промежуточных значений функции пользуются более сложной квадратичной интерполяцией или другими приемами [17].

2.3. Квадратичная интерполяция
Пусть снова дана функция f(x), заданная таблично. Считая, что на промежутке (x_k, x_k+2) данную функцию с достаточной степенью точности можно заменить квадратичной функцией, то есть часть графика функции можно заменить параболой (см. рис. 3), необходимо найти значение функции f(x) в некоторой точке x, принадлежащей интервалу (x_k, x_k+2).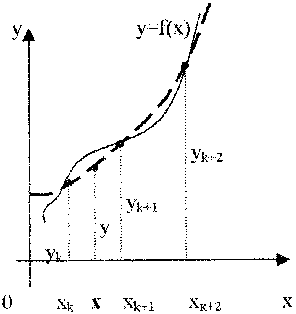

Рис. 3
Будем искать квадратичную функцию в следующем виде: .

Исходя из условия совпадения значений искомой квадратичной функции с табличными значениями функции в трех заданных точках, составим следующую систему уравнений: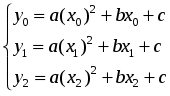

.

Это система трех линейных уравнений с тремя неизвестными a, b и с. Ее определитель не равен 0 (если только точки не лежат на одной прямой). Решая составленную систему уравнений матричным способом, получим следующую зависимость для коэффициентов а, b и с: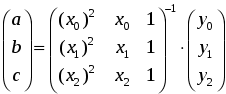

.

Таким образом значение функции f(х) в точке х можно приближенно считать равным

.

Естественно поставить вопрос о погрешности полученной формулы. Рассмотрим разность между точным значением функции f(х) и ее приближенным значением. Обозначим эту разность через j(х):

j(х)= f(х)-ax²-bx-c.

Мы подошли к задаче об оценке значений функции j(х) для х, пробегающих промежуток (х_к, х_к+2). В рассматриваемом случае нам придется предполагать, что третья производная функции f(х) на рассматриваемом промежутке непрерывна и удовлетворяет неравенству [27]:

| f(x)| £ M₃.

Тогда для j(х) справедлива следующая оценка:
.
ЛАБОРАТОРНАЯ РАБОТА №1
Задание:Используя линейную интерполяцию, вычислить значения функции у(х), заданной таблично, при заданном значении аргумента.
Образец выполнения задания
Зададим функцию таблично

n := 11 число значений аргумента

a := 2 начальное значение аргумента

h := 0.7 шаг изменения аргумента

i := 0.. n

x_i := a + ih значения аргумента

y_i := ln(x_i) + rnd(2) значения функции

таблицы значений х и у


графическое представление

заданной функции: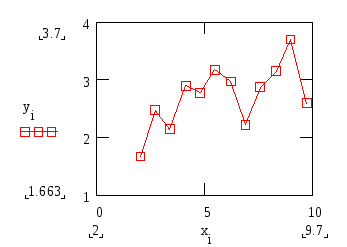




xx := 6.35 данное значение аргумента

ix := 6 номер табличного значения аргумента, ближайшего к данному
Найдем угловой коэффициент прямой, проходящей через 2 точки, ближайшие к хх.
j := ix - 1.. ix + 1



в уравнение искомой прямой подставим значение хх аргумента

yx := y_ix + k(xx - x_ix)

yx = 2.812

Проиллюстрируем решение графически: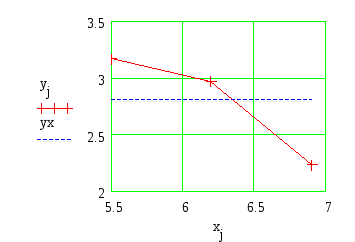

В пакете MathCad имеются встроенные функции, которые позволяют быстрее решить задачу линейной интерполяции. Это выполняется функцией linterp(vx,vy,x), которая использует векторы данных vx и vy, чтобы вычислить линейно интерполируемое значение у, соответствующее третьему аргументу х. Аргументы vx и vy должны быть одинаковой длины. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания. На рисунке 4 решена предложенная задача линейной интерполяции

.

ЛАБОРАТОРНАЯ РАБОТА №2
Задание:Используя квадратичную интерполяцию, вычислить значения функции у(х), заданной таблично, при заданном значении аргумента.
Образец выполнения задания
Зададим функцию таблично
n := 11 число значений аргумента

a := 2 начальное значение аргумента

h := 0.7 шаг изменения аргумента

i := 0.. n

x_i := a + ih + rnd(0.8) значения аргумента

y_i := ln(x_i) + rnd(2) значения функции
таблицы значений х и у


графическое представление

заданной функции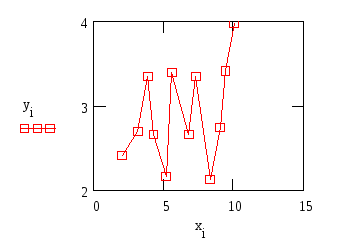

xx := 7.575 данное значение аргумента

ix := 7 номер табличного значения аргумента,

ближайшего к данному
Через 3 точки, ближайшие к хх (х₇, х₈, х₉) проведем параболу y(x)=ax²+bx+c, коэффициенты которой найдем по формуле: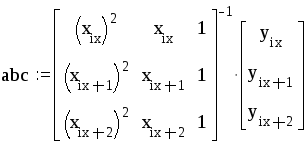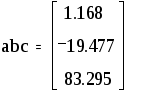




f(t) := abc₀t² + abc₁t + abc₂ Уравнение искомой параболы
yx := f(xx) в найденное уравнение подставим

значение хх аргумента

yx = 2.806

Проиллюстрируем решение графически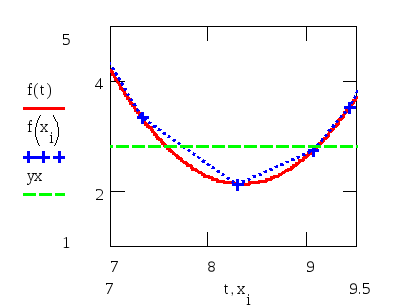



В пакете MathCad имеются встроенные функции, которые позволяют быстрее решить задачу квадратичной интерполяции. На рисунке 5 предлагается решение данной задачи.
3. Аппроксимация функций
3.1. Постановка задачи аппроксимации функции одной переменной
Пусть в результате измерений в процессе опыта получено табличное задание некоторой функции f(х), выражающей связь между двумя географическими параметрами:

х (1)	x1	х2	…	xn
f(x)	y1	у2	…	yn

Конечно, можно найти формулу, выражающую эту зависимость аналитически, применив метод интерполяции. Однако совпадение значений полученного аналитического задания функции в узлах интерполяции с имеющимися эмпирическими данными часто может вовсе не означать совпадение характеров поведения исходной и интерполирующей функции на всем интервале наблюдения. Кроме того, табличная зависимость географических показателей всегда получается в результате измерений различными приборами, имеющими определенную и не всегда достаточно малую погрешность измерения. Требование точного совпадения значений приближающей и приближаемой функций в узлах является тем более неоправданным, если значения функции f(х), полученные в результате измерений, уже сами являются приближенными.
Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей (1). Необходимо найти функцию заданного вида:

y=F(x), (2)

которая в точках x₁, x₂, …, x_n принимает значения, как можно более близкие к табличным y₁, y₂, …, y_n.

На практике вид приближающей функции чаще всего определяют путем сравнения вида приближенно построенного графика функции у= f(х) с графиками известных исследователю функций, заданных аналитически (чаще всего простых по виду элементарных функций). А именно: по таблице (1) строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции.

Рассмотрим рисунок 6: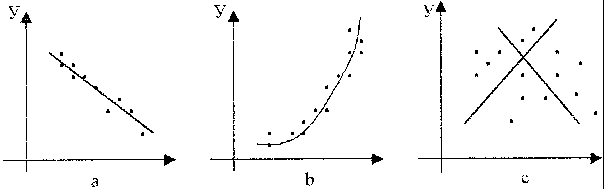

Рис. 6
На рисунке 6 изображены три ситуации:

 На графике а взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий.

 На графике b реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами.

 На графике с явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.

Следует заметить, что строгая функциональная зависимость для таблицы исходных данных наблюдается редко, ибо каждая из участвующих в ней величин может зависеть от многих случайных факторов. Однако формула (2) (ее называют эмпирической формулой, или уравнением регрессии у на х) интересна тем, что позволяет находить значения функции f для нетабличных значений х, «сглаживая» результаты измерений величины у, т.е. на всем интервале изменения х. Оправданность такого подхода определяется в конечном счете практической полезностью полученной формулы.
3.2. Метод наименьших квадратов
Через имеющееся «облако» точек всегда можно попытаться провести линию установленного вида, которая является наилучшей в определенном смысле среди всех линий данного вида, то есть «ближайшей» к точкам наблюдений по их совокупности. Для этого определим вначале понятие близости линии к некоторому множеству точек на плоскости. Меры такой близости могут быть различными [13]. Однако любая разумная мера должна быть связана с расстоянием от точек наблюдения до рассматриваемой линии (задаваемой уравнением y=F(x)).

Предположим, что приближающая функция F(x) в точках х₁, x₂,..., x_n имеет значения y₁, y₂,..., y_n. Часто в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений y_i. Здесь считается, что y_i и x_i – известные данные наблюдений, а F – уравнение линии регрессии с неизвестными параметрами (формулы для их вычисления будут приведены ниже). Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции, называется методом наименьших квадратов (МНК), или Least Squares Method (LS).

Итак, задачу приближения функции f теперь можно сформулировать следующим образом: для функции f, заданной таблицей (1), найти функцию F определенного вида так, чтобы сумма квадратов Ф была наименьшей.

.

Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:

. (3)

Пусть F(x_i, a, b, c) = y_i, i=1, 2,..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:

. (4)

Эта сумма является функцией Ф(а, b, c) трех переменных (параметров a, b и c). Задача сводится к отысканию ее минимума. Используем необходимое условие экстремума:

.

Получаем систему для определения неизвестных параметров a, b, c.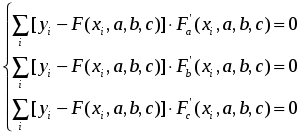

. (5)

Решив эту систему трех уравнений с тремя неизвестными относительно параметров a, b, c, мы и получим конкретный вид искомой функции F(x, a, b, c). Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, а выразится лишь в изменении количества уравнений в системе (5).

Естественно ожидать, что значения найденной функции F(x, a, b, c) в точках х₁, x₂,..., x_n, будут отличаться от табличных значений y₁, y₂,..., y_n. Значения разностей y_i-F(x_i,a, b, c)=e_i (i=1, 2,..., n) называются отклонениями измеренных значений y от вычисленных по формуле (3). Для найденной эмпирической формулы (2) в соответствии с исходной таблицей (1) можно, следовательно, найти сумму квадратов отклонений , которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (4) имеет наименьшее значение.

В экспериментальной практике в качестве приближающих функций в зависимости от характера точечного графика f часто используются приближающие функции с двумя параметрами:

1) y = ax + b,5) ,

2) y = ax² + bx + c,6) y = a  ln x,

3)y = ax^m, 7) ,

4)y = ae^mx, 8) .

Очевидно, что когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров.
3.3. Нахождение приближающей функции

в виде основных элементарных функций
Рассмотрим наиболее часто встречающиеся в практических исследованиях эмпирические зависимости.

3.3.1. Линейная функция (линейная регрессия). Начальным пунктом анализа зависимостей обычно является оценка линейной зависимости переменных. Следует при этом учитывать, однако, что «наилучшая» по методу наименьших квадратов прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y=f(x) является квадратичной, то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется «наилучшая». Если величины х и у вообще не связаны, мы также всегда сможем найти «наилучшую» линейную функцию y=ax+b для данной совокупности наблюдений, но в этом случае конкретные значения а и b определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности.

Рассмотрим теперь задачу оценки коэффициентов линейной регрессии более формально. Предположим, что связь между x и y линейна и искомую приближающую функцию будем искать в виде:

. (6)

Найдем частные производные по параметрам: .

Подставим полученные соотношения в систему вида (5):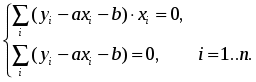



Далее имеем: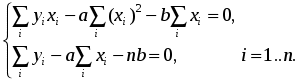



или, деля каждое уравнение на n: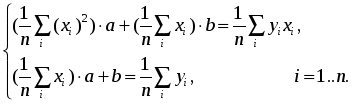



Введем обозначения: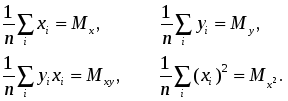

(7)

Тогда последняя система будет иметь вид: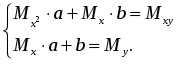

(8)

Коэффициенты этой системы M_x, M_y, M_xy, M_x² – числа, которые в каждой конкретной задаче приближения могут быть легко вычислены по формулам (7), где x_i, y_i – значения из таблицы (1). Решив систему (8), получим значения параметров a и b, а следовательно, и конкретный вид линейной функции (6).

Необходимым условием для выбора линейной функции в качестве искомой эмпирической формулы является соотношение [38]:

.

3.3.2. Квадратичная функция (квадратичная регрессия). Будем искать приближающую функцию в виде квадратного трехчлена:

. (9)

Находим частные производные: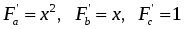

.

Составим систему вида (5):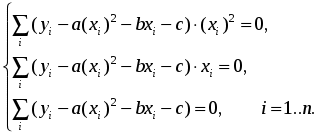



После несложных преобразований получается система трех линейных уравнений с тремя неизвестными a, b, c. Коэффициенты системы так же, как и в случае линейной функции, выражаются только через известные данные из таблицы (1):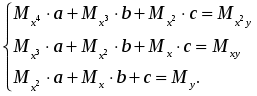

(10)

Здесь использованы обозначения (7), а также



Решение системы (10) дает значение параметров a, b и с для приближающей функции (9).

Квадратичная регрессия применяется, если все выражения вида
у₂ -2y₁ +y_0, y₃ -2 y₂ + y_1, y₄ -2 y₃ + y₂ и т.д. мало отличаются друг от друга.

3.3.3. Степенная функция (геометрическая регрессия). Найдем теперь приближающую функция в виде:

. (11)

Предполагая, что в исходной таблице (1) значения аргумента и значения функции положительны, прологарифмируем равенство (11) при условии а>0:

. (12)

Так как функция F является приближающей для функции f, функция lnF будет приближающей для функции lnf. Введем новую переменную u=lnx; тогда, как следует из (12), lnF будет функцией от u: Ф(u).

Обозначим

. (13)

Теперь равенство (12) принимает вид:

, (14)

т.е. задача свелась к отысканию приближающей функции в виде линейной. Практически для нахождения искомой приближающей функции в виде степенной (при сделанных выше предположениях) необходимо проделать следующее:

1) по данной таблице (1) составить новую таблицу, прологарифмировав значения x и y в исходной таблице;

2) по новой таблице найти параметры А и В приближающей функции вида (14);

3) использовав обозначения (13), найти значения параметров a и m и подставить их в выражение (11).

Необходимым условием для выбора степенной функции в качестве искомой эмпирической формулы является соотношение [38]:

.

3.3.4. Показательная функция. Пусть исходная таблица (1) такова, что приближающую функцию целесообразно искать в виде показательной функции:

. (15)

Прологарифмируем равенство (15):

. (16)

Приняв обозначения (13), перепишем (16) в виде:

. (17)

Таким образом, для нахождения приближающей функции в виде (15) нужно прологарифмировать значения функции в исходной таблице (1) и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы приближающую функцию вида (17). Вслед за этим в соответствии с обозначениями (13) остается получить значения искомых параметров a и b и подставить их в формулу (15).

Необходимым условием для выбора показательной функции в качестве искомой эмпирической формулы является соотношение [38]:

.

3.3.5. Дробно-линейная функция. Будем искать приближающую функцию в виде:

. (18)

Равенство (18) перепишем следующим образом:

.

Из последнего равенства следует, что для нахождения значений параметров a и b по заданной таблице (1) нужно составить новую таблицу, у которой значения аргумента оставить прежними, а значения функции заменить обратными числами, после чего для полученной таблицы найти приближающую функцию вида ax+b. Найденные значения параметров a и b подставить в формулу (18).

Необходимым условием для выбора дробно-линейной функции в качестве искомой эмпирической формулы является соотношение [38]:

.

3.3.6. Логарифмическая функция. Пусть приближающая функция имеет вид:

. (19)

Легко видеть, что для перехода к линейной функции достаточно сделать подстановку lnx=u. Отсюда следует, что для нахождения значений a и b нужно прологарифмировать значения аргумента в исходной таблице (1) и, рассматривая полученные значения в совокупности с исходными значениями функции, найти для полученной таким образом новой таблицы приближающую функцию в виде линейной. Коэффициенты a и b найденной функции подставить в формулу (19).

Необходимым условием для выбора логарифмической функции в качестве искомой эмпирической формулы является соотношение [38]:

.

3.3.7. Гипербола. Если точечный график, построенный по таблице (1), дает ветвь гиперболы, приближающую функцию можно искать в виде:

. (20)

Для перехода к линейной функции сделаем подстановку .

. (21)

Практически перед нахождением приближающей функции вида (20) значения аргумента в исходной таблице (1) следует заменить обратными числами и найти для новой таблицы приближающую функцию в виде линейной вида (21). Полученные значения параметров а и b подставить в формулу (20).

Необходимым условием для выбора уравнения гиперболы в качестве искомой эмпирической формулы является соотношение [38]:

.

3.3.8. Дробно-рациональная функция. Пусть приближающая функция находится в виде:

. (22)

Очевидно, что

,

так что задача сводится к случаю, рассмотренному в предыдущем пункте. Действительно, если в исходной таблице заменить значения х и у их обратными величинами по формулам и и искать для новой таблицы приближающую функцию вида u=bz+a, то найденные значения а и b будут искомыми для формулы (22).

Необходимым условием для выбора дробно-рациональной функции в качестве искомой эмпирической формулы является соотношение [38]:

.

В заключение отметим: может получиться, что ни одна из рассмотренных выше функций не приближает достаточно удовлетворительно имеющиеся эмпирические данные. В таком случае вид эмпирической кривой выбирают исходя из каких-то других известных данных о поведении функции. Иногда это помогают сделать специальные компьютерные программы аппроксимации экспериментальных данных [38].
ЛАБОРАТОРНАЯ РАБОТА №3
Задание: Аппроксимировать функцию, заданную таблично, линейной функцией.
Образец выполнения задания
Зададим функцию таблично

n := 11 число значений аргумента

a := 2 начальное значение аргумента

h := 0.7 шаг изменения аргумента

aa := 0.3 bb := 0.7 числовые коэффициенты

i := 0.. n

x_i := a + ih значения аргумента

yc_i := (-1)ⁱrnd(1) + aa + bbx_i значения функции, случайная добавка
(-1)ⁱrnd(1) позволяет придать данным естественный вид.
Графическое представление полученной функции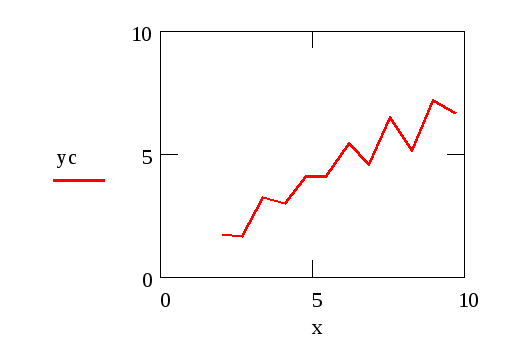


Воспользуемся формулами для вычисления коэффициентов линейной зависимости:




y_i := ab₀ + ab₁x_i искомая линейная функция
Проиллюстрируем решение графически: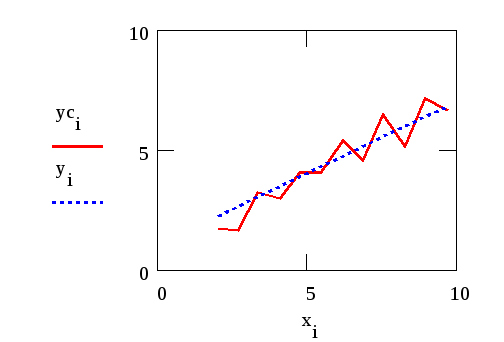

В пакете MathCad имеются встроенные функции, которые позволяют быстрее решить задачу линейной регрессии. Это выполняется функцией slope(vx,vy), которая вычисляет наклон линии регрессии в смысле наименьших квадратов для данных из vx и vy, и функцией intercept(vx,vy), которая вычисляет смещение по оси ординат линии регрессии. Окончательно линия регрессии определяется в виде:

y= slope(vx,vy)*x+ intercept(vx,vy)

На рисунке 7 показано, как можно использовать эти функции, чтобы провести линию через набор выборочных точек.
4. Множественная линейная регрессия
4.1. Понятие функции нескольких переменных
До сих пор мы касались вопросов, связанных с исследованием функции одной переменной, т.е. изучали совместное изменение двух переменных, одна из которых зависела от другой. Значением независимой переменной полностью определялось значение зависимой переменной, или функции. На практике значения географических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. Например, хотя продуктивность водоема и зависит от продолжительности солнечного освещения, но очевидно, что это не единственный определяющий фактор, здесь важны и интенсивность освещения, и загрязненность водоема, и его географическое расположение, а также целый ряд дополнительных факторов. Таким образом, независимых переменных часто оказывается несколько, и для определения значения функции необходимо установить значения, совместно принимаемые всеми этими независимыми переменными. В таком случае зависимость y=f(x) означает, что х – вектор, содержащий m компонентов: x=(x_1, x₂,..., x_m).
4.2. Постановка задачи множественной линейной регрессии
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f:

x1			...
x2			...
...	...	...	...	...
xm			...
y=f()	y1	y2	...	yn

Требуется найти формулу, выражающую эту зависимость аналитически, т.е. найти функцию заданного вида y=F(x_1, x₂,..., x_m), которая в точках x_1, x₂,... x_n принимает значения, как можно более близкие к значениям
y₁, y₂,... y_n.

Мы будем говорить только о линейной зависимости у от х, то есть о множественной линейной регрессии. Теоретически уравнение y=F(x) имеет вид:

y=a₀+a₁x₁₊ a₂ x₂ +... +a_mx_m.

Здесь а – вектор неизвестных параметров размерности (m+1).

Мы ограничимся рассмотрением частного случая m=2. Тогда приближающая функция примет следующий вид:

F(x) =a₀+a₁x₁₊a₂ x₂.

Пусть имеется n наблюдений вектора х и зависимой переменной у. Для того, чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть n ³ m+1. Если это условие не выполняется, то можно найти бесконечно много разных векторов коэффициентов, при которых линейная формула связывает между собой х и у для имеющихся наблюдений абсолютно точно. Если в частном случае n=m+1 (например, при m=2 и n=3), то оценки коэффициентов а рассчитываются единственным образом – путем решения системы линейных уравнений y_j=a₀+a₁x_1j+a₂x_2j; j=1,...3. Графически это означает, что через три точки наблюдения в трехмерном пространстве можно провести единственную плоскость, определяемую параметрами a₀, a₁, a₂. Если число наблюдений больше минимально необходимого, то есть n>3, то уже нельзя подобрать линейную формулу, в точности удовлетворяющую всем наблюдениями, и возникает необходимость оптимизации, то есть выбора наилучшей формулы-приближения для всех наблюдений.

Более подробно с вопросом приближения функций нескольких переменных можно ознакомиться в [13, 18].