Математические методы в географии Учебное пособие - Гриценко В.А., и др.. Математические методы в географии Учебное пособие - Гриценко В. Учебное пособие Калининград 1999
 Скачать 3.78 Mb. Скачать 3.78 Mb.
|
|
Глава 4. ПРАКТИЧЕСКИЙ ГАРМОНИЧЕСКИЙ АНАЛИЗ С древних времен отмечалось, что многие природные процессы являются периодическими или почти периодическими явлениями, то есть такими, которые воспроизводятся в прежнем виде через определенный промежуток времени Т, называемый периодом. Таковыми, например, являются смена времен года, дня и ночи, продолжительность светового дня и т.д. С точки зрения математики, различные величины, связанные с рассматриваемыми периодическими явлениями, по истечении периода Т возвращаются к своим прежним значениям и представляют, следовательно, периодические функции от времени t: f(t+T) = f(t). Простейшей из периодических функций является синусоидальная величина: где есть частота, связанная с периодом Т. Однако далеко не каждый природный процесс можно описать функцией указанного вида. 1. Постановка задачи гармонического анализа Из простейших периодических функций могут быть составлены более сложные. При этом составляющие синусоидальные величины должны быть разных частот, так как сложение синусоидальных величин одной и той частоты не дает ничего нового, а приводит к синусоидальной величине той же частоты. Естественно, встает обратный вопрос: можно ли данную периодическую функцию f(t) периода Т представить в виде суммы конечного или хотя бы бесконечного множества синусоидальных величин. Как известно из классического анализа, по отношению к достаточно широкому классу функций на этот вопрос можно дать утвердительный ответ, то есть для них имеет место разложение в тригонометрический ряд или ряд Фурье. Геометрически это означает, что график периодической функции получается путем наложения ряда синусоид. Если же истолковать каждую синусоидальную величину механически, как представляющую гармоническое колебательное движение, то можно также сказать, что в этом случае сложное колебание (каковыми являются все колебания, встречающиеся в природе), характеризуемое функцией f(t), разлагается на отдельные гармонические колебания. В связи с этим отдельные синусоидальные величины, входящие в состав тригонометрического ряда, называют гармоническими составляющими функции f(t), или просто ее гармониками (первой, второй и т.д.) Сам процесс разложения периодической функции на гармоники носит название гармонического анализа [27]. Итак, гармоническим анализом называют операцию разложения заданной периодической функции f(x) в ряд Фурье. Если функция f(x) задана аналитически, то задача ее гармонического анализа полностью решается с помощью известных из классического анализа формул Эйлера-Фурье для вычисления коэффициентов ряда Фурье. Однако в огромном числе практических задач подлежащая анализу функция f(x) оказывается заданной в виде таблицы, полученной в результате измерений, или в виде кривой, вычерченной самопишущим прибором. Тогда точное вычисление коэффициентов Фурье по формулам Эйлера-Фурье невозможно. Таким образом, в нашем случае задача гармонического анализа заключается в построении практически удобных методов для приближенного определения коэффициентов ряда Фурье или для непосредственного вычерчивания гармоник различных порядков для функции, заданной таблично. 2. Разложение функций в ряд Фурье Будем предполагать, что функция f(x) – периодическая, с периодом 2 (f(x+2р)=f(x)). Как известно, это всегда обеспечивается соответствующим изменением масштаба по оси Ох. Основная задача гармонического анализа состоит в представлении функции f(x) в виде ряда: Полагая ряд (1) можно переписать в виде: Здесь сn – амплитуда гармоники, n – фаза. Коэффициенты ряда (1) – ряда Фурье – определяют по формулам Эйлера-Фурье: 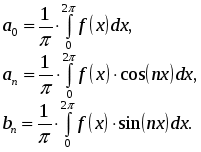 (4) (4)Пусть промежуток от 0 до 2 разделен точками x1, x2, …, xk-1 (xi=2i/k) на k равных частей и пусть известны соответствующие ординаты – y0, y1, y2,…, yk-1, yk=y0. Тогда для вычисления интегралов в формулах (4) можно применить различные приближенные методы. Так, по формуле трапеций получим: Отсюда в силу того, что y0=yk, Аналогично для определения коэффициентов an и bn формула трапеций дает: Окончательно получим: 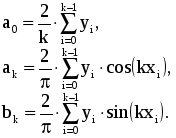 Последние формулы носят название формул Бесселя. Они могут быть получены из формул для коэффициентов Фурье (4) функции f(x), если вычислять входящие в них интегралы приближенно, используя формулу трапеций, полагая f(0)=f(2) [4]. Заметим, что значения а0, ak, bk, полученные по формулам Бесселя, будут близки к значениям коэффициентов Фурье функции только при относительно небольших к. В остальных случаях расхождение будет больше. ЛАБОРАТОРНАЯ РАБОТА №7 Задание: Разложить заданную функцию в ряд Фурье. Образец выполнения задания Зададим функцию таблично N := 100 a1 := 1 a2 := .5 a3 := -.1 i := 1.. N xi := i dt значенияаргумента yi := a1sin(xi) + a2sin(4xi) + a3cos(5xi) значения функции, являющейся суммой трех гармонических колебаний. Графическое представление заданной функции подтверждает наличие периодических составляющих: 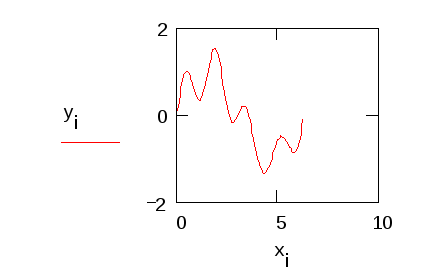 Воспользуемся формулами Бесселя для вычисления коэффициентов a0, ak, bk: 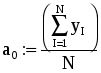 n := 15 k := 1.. n Значение 15 выбрано в Связи с возможностью РС 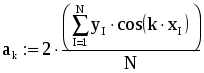 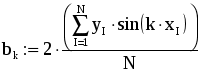 Учитывая, что при небольших к коэффициенты a0, ak, bk будут близки к коэффициентам Фурье функции f(x), получим: i := 1.. N 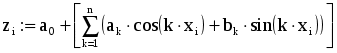 Графическое представление полученной функции (на рис. 15 представлены различные виды приближающей функции в зависимости от значения n): 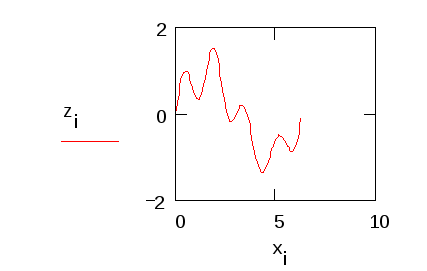 Таким образом, графики иллюстрируют близость заданной функции и приближающего ее тригонометрического ряда. Глава 5. СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ Выполнение комплексных научных исследований, а также проектирование и строительство промышленных, сельскохозяйственных и транспортных объектов требуют календарной увязки большого числа взаимосвязанных работ, выполняемых различными организациями. Составление и анализ соответствующих календарных планов представляют собой весьма сложную задачу, при решении которой применяются так называемые методы сетевого планирования. По существу, этот метод дает возможность определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта, и, во-вторых, каким образом построить наилучший календарный план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах. Первый вариант этого метода был разработан в 1957 году американским ученым Дж.Е. Келли и М.Р. Уокером и был назван СРМ (от начальных букв выражения «Critical Path Method», означающего «Метод критического пути»). Примерно в то же время независимо от СРМ появилась система PERT («Program Evaluation and Review Technique», что означает «Техника обзора и оценки программ»). В результате дальнейшего развития эти системы превратились в совокупную методику построения графиков – сетевое планирование и управление. Идея сетевого метода очень проста. Она основана на графическом изображении комплекса работ с любой степенью их детализации и на выполнении элементарных арифметических операций по расчету параметров и анализу сетевых графиков. 1. Элементы и правила построения сетевых графиков Система сетевого планирования основана на безмасштабном графическом изображении комплекса операций, показывающем технологическую последовательность и логическую взаимозависимость между всеми работами, направленными на достижение определенной цели. Сетевой график (стрелочная диаграмма, сетевая модель, или просто сеть) состоит из стрелок и кружков, обозначающих два основных элемента любой сети – работы и события. Работа – это реальный процесс или действие, требующее затрат труда, материалов или времени. Продолжительность выполнения работ измеряется в единицах времени: часах, днях, неделях, месяцах и т.д. Работы могут иметь также и количественные показатели, которые характеризуют трудоемкость, стоимость, материальные ресурсы и т.д. Работы обозначаются стрелками, которые объединяются между собой с помощью кружков (событий). Временные и количественные оценки проставляются обычно над стрелками. Событием называется результат, получаемый после выполнения работ, стрелки которых сходятся к данному кружку. Событие имеет двойное значение. Для всех предшествующих работ оно является законченным свершением, а для последующих работ – начальным пунктом их выполнения. Всем событиям присваивается определенный цифровой шифр, который проставляется обычно внутри кружка. В общем смысле начальное (предшествующее) событие обозначается буквой i, а конечное (последующее) – буквой j, работа в этом случае обозначается как i, j. Во всяком сетевом графике бывает два особых события, которые не имеют двойного значения – исходное и завершающее. Исходное событие – это момент начала выполнения комплекса работ. Оно не является результатом предыдущих работ, поэтому в него не входит ни одной стрелки. Исходные события принято обозначать буквой J. К особенностям завершающего события относится то, что оно свидетельствует об окончании всех работ и поэтому не имеет ни одной последующей работы. Из этого события не выходит ни одной стрелки. Обозначается оно буквой С. Пример 1. Необходимо собрать узел из двух деталей А и Б. Обе детали должны быть обработаны на токарном станке, деталь Б должна пройти, кроме того, шлифовку. Перечень событий, а также данные о продолжительности работ (в минутах) приведены в табл.1, 2. Таблица 1
График этого проекта показан на рис. 1. Таблица 2
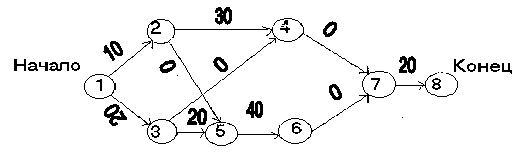 Рис. 1 Для получения безошибочной структуры сетевых графиков при их построении необходимо соблюдать следующие основные правила: - в сетевом графике не должно быть тупиков, т.е. событий, из которых не выходит ни одной работы (за исключением завершающего события); - сеть не должна иметь «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа; - в сети не должно быть замкнутых контуров (циклов); - в сетевой модели не допускаются работы, имеющие одинаковые шифры; - любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой; - в сети рекомендуется иметь одно исходное и одно завершающее события. При построении сети исходное событие располагается с левой стороны, а завершающее – с правой. Нумерация событий обычно начинается с исходного и заканчивается на завершающем событии. Для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием. 2. Понятие пути сетевого графика Одно из важнейших понятий сетевого графика – понятие пути. Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути. По существу, критический путь – «узкое» место проекта. Уменьшить общую продолжительность осуществления проекта можно, только изыскав способы сокращения работ, лежащих на критическом пути. Таким образом, нет никакой необходимости в часто практикуемом стремлении «поднажать» на всех работах ради сокращения общей длительности выполнения проекта. В больших проектах критическими бывают примерно 10% работ. Для рассмотренного в примере 1 сетевого графика полными путями будут: путь 1®2®4®7®8 (продолжительностью 10+30+0+20=60 минут), путь 1®2®5®6®7®8 (продолжительностью 10+0+40+0+20=70 минут), путь 1®3®4®7®8 (продолжительностью 20+0+0+20=40 минут), путь 1®3®5®6®7®8 (продолжительностью 20+20+40+0+20=100 минут). Последний путь имеет наибольшую продолжительность и является критическим. Продолжительность критического пути составляет 100 минут. Быстрее работу выполнить нельзя, так как для достижения завершающего события критический путь надо пройти обязательно. Время, необходимое для выполнения некритических работ, не имеет значения с точки зрения продолжительности осуществления проекта в целом. Иначе говоря, все ненапряженные пути имеют резервы времени. Эти резервы определяются вычитанием из критического пути продолжительности данного некритического пути. 3. Временные параметры сетевых графиков В таблице 3 приведены основные временные параметры сетевых графиков. Важнейшим показателем сетевого графика являются резервы времени [20]. Резервы времени каждого пути показывают, на сколько может быть увеличена продолжительность данного пути без ущерба для наступления завершающего события. Поскольку каждый некритический путь сетевого графика имеет свой полный резерв времени, то и каждое событие этого пути имеет свой резерв времени. Таблица 3
Для определения резервов времени по событиям сети рассчитывают наиболее ранние (tp)и наиболее поздние (tп) сроки свершения событий. Любое событие не может наступить прежде, чем свершатся все предшествующие ему события и не будут выполнены все предшествующие работы. Поэтому ранний (или ожидаемый) срок tp(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию: где Lni – любой путь, предшествующий i-му событию, то есть путь от исходного до i-го события сети. Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле: Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из следующих за ним путей не превысит длины критического пути. Поэтому поздний (или предельный) срок tп(i) свершения i-го события равен: где Lci – любой путь, следующий за i-м событием, т.е. путь от i-го до завершающего события сети. Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле: Резерв времени R(i) i-го события определяется как разность между поздним и ранним сроками его свершения: Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ. Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Таким образом, определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути. В качестве примера определим временные параметры событий и критический путь для сетевого графика, изображенного на рис. 1. Найденные параметры сведем в таблицу 4. При определении ранних сроков свершения событий tp(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2). Для i=1 (начального события) tp(1)=0. Для i=2 tp(2)= tp(1)+ +t(1,2)=0+10=10 (мин), так как для события 2 существует только один предшествующий путь 1®2. Для i=3 tp(3)= tp(1)+ t(1,3)=0+20=20, так как для события 3 существует один предшествующий путь 1®3. Для i=4 tp(4)=max{ tp(2)+ t(2,4); tp(3)+t(3,4)}={10+30;20+0}=40, так как для события 4 существуют два предшествующих пути 1®2®4 и 1®3®4 и два предшествующих события – 2 и 3. Аналогично определяем сроки раннего начала для остальных событий сети: tp(5)= max{ tp(2)+t(2,5); tp(3)+t(3,5)}=max{10+0; 20+20}=max{10;40}=40; tp(6)= tp(5)+t(5,6)=40+40=80; tp(7)= max{ tp(4)+t(4,7); tp(6)+t(6,7)}=max{40+0; 80+0}=max{40;80}=80; tp(8)= tp(7)+t(7,8)=80+20=100. Длина критического пути равна раннему сроку свершения завершающего события 8: tkp=tp(8)=100 (мин). Таблица 4
При определении поздних сроков свершения событий tп(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4). Для i=8 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): tп(8)= tр(8)=100 (мин). Для i=7 tп(7)= tп(8)- t(7,8)=100-20=80, так как для события 7 существует только один последующий путь 7®8. Для i=6 tп(6)= tп(7)- t(6,7)=80-0=80, так как для события 6 существует только один последующий путь 6®7®8. Для i=5 tп(5)= tп(6)- t(5,6)=80-40=40, так как для события 5 существует только один последующий путь 5®6®7®8. Для i=4 tп(4)= tп(7)- t(4,7)=80-0=80, так как для события 4 существует только один последующий путь 4®7®8. Для i=3 tп(3)=min{tп(4)- t(3,4); tп(5)- t(3,5)}=min{80-0; 40-20}=min{80; 20}=20, так как для события 3 существует два последующих пути 3®4®7®8 и 3®5®6®7®8. Для i=2 tп(2)=min{ tп(4)- t(2,4); tп(5)- t(2,5)}=min{80-30; 40-0}=min{50; 40}=40, так как для события 2 существует два последующих пути 2®4®7®8 и 2®5®6®7®8. Для i=1 tп(1)=min{ tп(2)- t(1,2); tп(3)- t(1,3)}=min{40-10; 20-20}=min{30; 0}=0. По формуле (5) определяем резервы времени i-го события: R(1)=0; R(2)=30; R(3)=0 и т.д. Резерв времени события 2 - R(2)=30 означает, что время свершения события 2 может быть задержано на 30 минут без увеличения общего срока выполнения проекта. Анализируя таблицу 4, видим, что не имеют резервов времени события 1,3,5,6,7,8. Эти события и образуют критический путь. Теперь перейдем к параметрам работ. Отдельная работа может начаться (и окончиться) в ранние, поздние и другие промежуточные сроки. При оптимизации графика возможно любое размещение работы в заданном интервале. Очевидно, что ранний срок tрн(i,j) начала работы (i,j) совпадает с ранним сроком наступления начального (предшествующего) события i, то есть tрн(i,j)= tр(i). (6) Тогда ранний срок tро(i,j) окончания работы (i,j) определяется по формуле tро(i,j)= tр(i)+ t(i,j). (7) Ни одна работа не может окончиться позже допустимого позднего срока своего конечного события j. Поэтому поздний срок tпо(i,j) окончания работы (i,j) определяется соотношением: tпо(i,j)= tп(j), (8) а поздний срок tпн(i,j) начала этой работы – соотношением tпн(i,j)= tп(j)- t(i,j). (9) Прежде чем рассматривать резервы времени работ, обратимся к резерву времени пути. Такие резервы имеют все некритические пути. Резерв времени пути определяется как разность между длиной критического и рассматриваемого пути: R(L)= tkp-t(L). (10) Он показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Любая из работ пути L на его участке, не совпадающем с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени. Полный резерв времени Rп(i,j) работы (i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв Rп(i,j) определяется по формуле: Rп(i,j)= tп(j)- tр(i)- t(i,j). (11) Полный резерв времени работы равен резерву максимального из путей, проходящего через данную работу. Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок, и можно допустить свершение ее конечного события в самый поздний срок. Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее. Работы, лежащие на критическом пути, так же, как и критические события, резервов времени не имеют. Вычислим в качестве примера временные параметры работ для сетевого графика, изображенного на рис. 1. Результаты вычислений сведем в таблицу 5. Таблица 5
Вычисление временных параметров работы (i,j) покажем на примере работы (2,4). Ранний срок начала работы (по формуле (6)): tрн(2,4)= tр(2)=10. Ранний срок окончания работы (по формуле (7)): tро(2,4)= tр(2)+ t(2,4)=10+30=40. Поздний срок начала работы (по формуле (9)): tпн(2,4)= tп(4)- t(2,4)=80-30=50. Поздний срок окончания работы (по формуле (8)): tпо(2,4)= tп(4)=80. Таким образом, работа (2,4) должна начаться в интервале [10, 50] и окончиться в интервале [40, 80] от начала выполнения проекта. Полный резерв времени работы (2,4) (по формуле (11)): Rп(2,4)= tп(4)- tр(2)- t(2,4)=80-10-30=40, то есть срок выполнения данной работы можно увеличить на 40 минут, при этом срок выполнения комплекса работ не изменится. Покажем на примере работы (2,4), что полный резерв времени работы равен резерву максимального из путей, проходящих через эту работу. Через работу (2,4) проходит один полный путь: 1®2®4®7®8 продолжительностью 60 минут. По формуле (10) его резерв R(L)= tkp-t(L)=100-60=40. Как видим, полный резерв времени работы (2,4) равен резерву времени максимального (и единственного) полного пути, проходящего через эту работу. Если увеличить продолжительность работы (2,4) на 40 минут, то полностью будет исчерпан резерв времени этого пути, то есть этот путь станет также критическим. Следует отметить, что кроме полного резерва времени работы выделяют еще три разновидности резервов. Частный резерв времени первого вида R1 – часть полного резерва времени, на которое можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R1 находится по формуле: R(i,j)= Rп(i,j)- R(i). (12) Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которое можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле: Rс(i,j)= Rп(i,j)- R(j). (13) Независимый резерв времени Rн работы (i,j) – часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле: Rн(i,j)= Rп(i,j)- R(i)- R(j). (14) Более подробно узнать о применении вышеперечисленных данных можно в [8], [20]. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
