Математические методы в географии Учебное пособие - Гриценко В.А., и др.. Математические методы в географии Учебное пособие - Гриценко В. Учебное пособие Калининград 1999
 Скачать 3.78 Mb. Скачать 3.78 Mb.
|
|
4. Некоторые замечания об оптимизации плана Оптимизация сетевого графика представляет собой процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Она проводится с целью сокращения длины критического пути, рационального использования ресурсов. В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается: перераспределением всех видов ресурсов – как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических; сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени; параллельным выполнением работ критического пути; изменением состава работ и структуры сети. В процессе сокращения продолжительности работ критический путь может измениться и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути, и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути. Тогда все работы будут вестись с равным напряжением, а срок выполнения проекта существенно сократится. Дополнительно о методах оптимизации сетевого графика можно узнать в [8], [20]. ЗАКЛЮЧЕНИЕ Заключение в конце учебного пособия, вообще говоря, и не обязательно. Однако внимательный и увлеченный работой читатель вполне имеет право спросить: «Ну и что?!» Действительно, что же получил студент-географ от знакомства с основными математическими приемами и подходами, используемыми при обработке экспериментальных данных? Авторы надеются, что это прежде всего осознание обыденности процедуры использования математики в качестве рабочего инструмента при исследовании природных явлений. Вторая грань приобретения будущего специалиста – это уверенность в безусловной реализуемости при помощи компьютера всех описанных в пособии процедур. Наконец, многочисленные ошибки и описки, допускаемые всеми исследователями в процессе подготовки действительно работающего проекта или программы, заставили приобрести уважение к процедуре проверки получаемых компьютером результатов. Все это в совокупности, освоенное и ставшее практическими навыками, заметно повышает класс специалиста. И последнее. И математика, и компьютер отнюдь не являются универсальной волшебной палочкой в исследовании природных процессов, по мановению которой удается решить любые научные задачи и проблемы. Подчеркнем, что только творческое использование всех возможных методов исследований и подходов может помочь заметно продвинуться в решении реальных задач. Поэтому – пробуйте, и у вас получится! РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Абрамов А.М., Виленкин Н.Я., Дорофеев Г.В. и др. Избранные вопросы математики. М.: Просвещение, 1980. 191 с. 2. Акоф Р., Сасиени М. Основы исследования операций. М.: Мир, 1971. 3. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. М.: Мир, 1974. 367 с. 4. Березин И.С., Жидков Н.П. Методы вычислений. М.: Гос. изд-во физико-математической литературы, 1959. 464 с. 5. Берлинер Э.М., Глазырин Б.Э., Глазырина И.Б. Microsoft Windows-95. Русская версия. М.: ABF, 1996. 427 с. 6. Вагнер Г. Основы исследования операций: В 3 т. М.: Мир, 1972. 7. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. М.: Высшая школа, 1990. 208 с. 8. Воронин В.Г. Математические методы планирования и управления на предприятиях пищевой промышленности. М.: Пищевая промышленность, 1971. 320 с. 9. Вычислительная математика: Методические указания, теоретический курс и контрольные задания / Под ред. проф. А.И. Бояринова. М.: Высшая школа, 1984. 112 с. 10. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. М.: Наука, 1970. 432 с. 11. Данилина Н.И., Дубровская Н.С., Кваша О.П., Смирнов Г.Л. Вычислительная математика. М.: Высшая школа, 1985. 472 с. 12. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в примерах и задачах: В 2 ч. М., 1980. 13. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Гос. изд-во физико-математической литературы, 1962. 368 с. 14. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970. 664 с. 15. Джонс Дж. К. Методы проектирования. М.: Мир, 1986. 326 с. 16. Дэвис Дж. Статистика и анализ геологических данных.: М.: Мир, 1977. 17. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. М.: Просвещение, 1990. 176 с. 18. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. М.: ДИС, 1997. 368 с. 19. Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с. 20. Карасев А.И., Кремер Н.Ш., Савельева Т.И. М.: Экономика, 1987. 241 с. 21. Коплан-Дикс И.С. Основы статистической обработки и картирования океанографических данных. Л.: Гидрометеоиздат, 1968. 129 с. 22. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука, 1972. 367 с. 23. Матвеев Н.М. Дифференциальные уравнения. Минск.: Вышэйшая школа, 1968. 348 с. 24. Математические методы в географии: Учебник. Казань: Изд-во Казанского ун-та, 1976. 352 с. 25. Математическое моделирование. М.: Мир, 1979. 277 с. 26. Матэр П. Компьютеры в географии. М.: Прогресс, 1981. 27. Норкин С.Б., Берри Р.Я., Жабин И.А. и др. Элементы вычислительной математики. М.: Высшая школа, 1963. 212 с. 28. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. М.: Наука, 1986. 288 с. 29. Самнер Г. Математика для географов. М.: Прогресс, 1981. 296 с. 30. Смит Дж. Математические идеи в биологии. М.: Мир, 1970. 31. Трофимов А.М. Математические методы в географии. Казань, 1977. 32. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. М.: Финансы и статистика, 1995. 384 с. 33. Фигурнов В.Э. IBM PC для пользователя. М., 1997. 34. Фихтенгольц Г.М. Основы математического анализа. Т. 1, 2. М., 1964. 464 с. 35. Франкен Г., Молявко С. MS-DOS 6.2... для пользователя. Киев.: BHV, 1994. 446 с. 36. Фурунжиев Р.И., Бабушкин Ф.М., Варавко В.В. Применение математических методов и ЭВМ. Минск: Вышэйшая школа, 1988. 191 с. 37. Харвей Д. Научное объяснение в географии. М.: Прогресс, 1979. 38. Янпольский А.Р. Лабораторный вычислительный практикум. М.: ВИА, 1968. 180 с. 39. MathCad 6.0 Plus. Финансовые, инженерные и научные расчеты в среде Windows 95. М.: Информационно-издательский дом «Филин», 1996. 712 с. 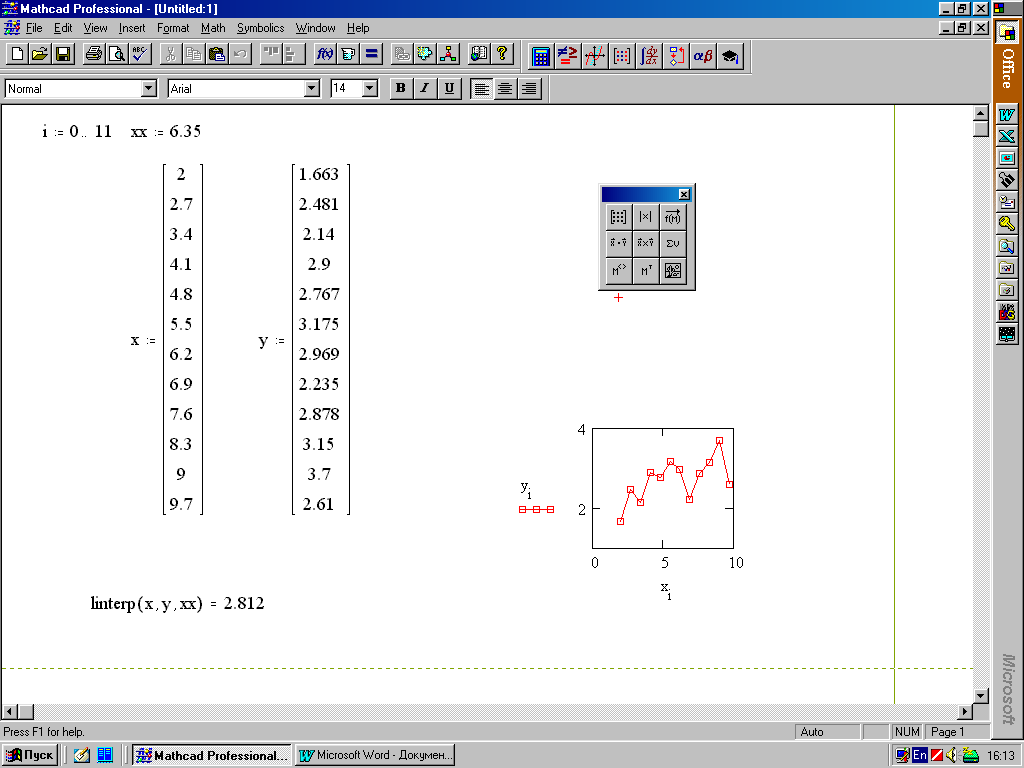 Рис.4. Решение задачи линейной интерполяции 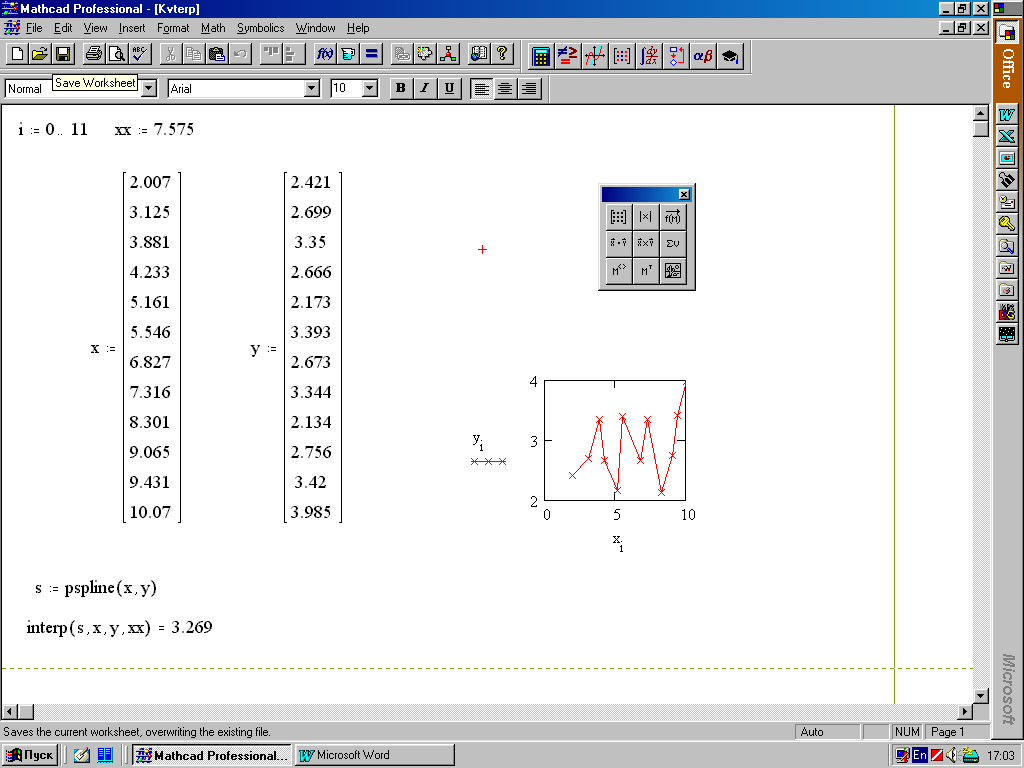 Рис.5. Решение задачи квадратичной интерполяции 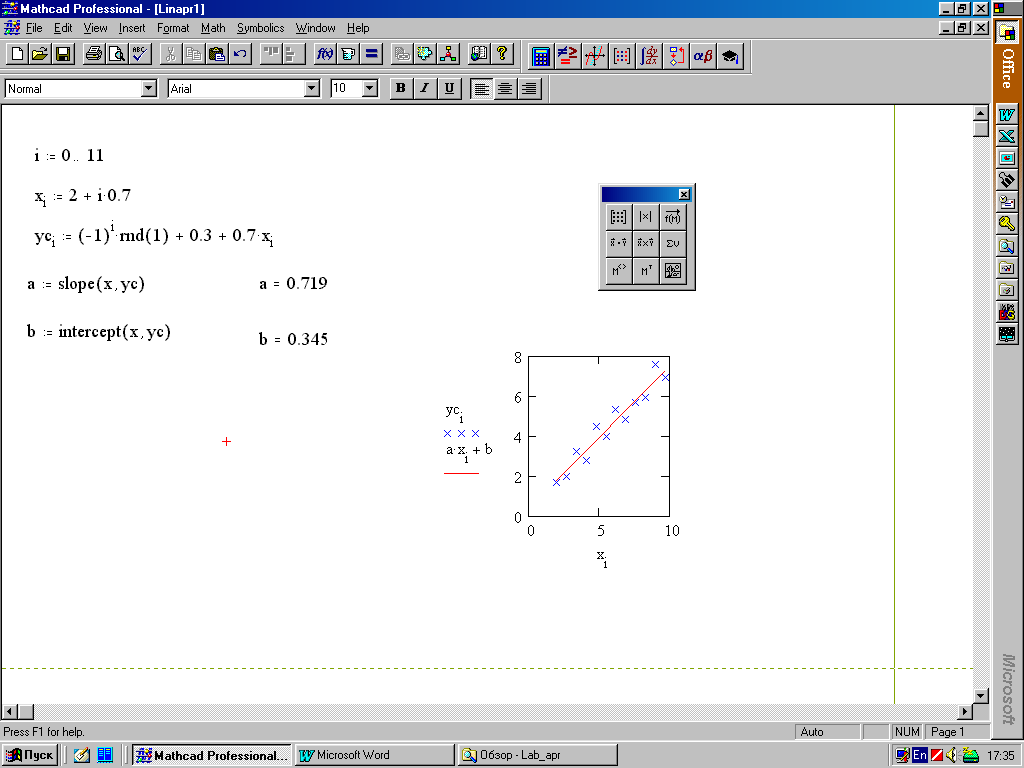 Рис.7. Решение задачи линейной аппроксимации 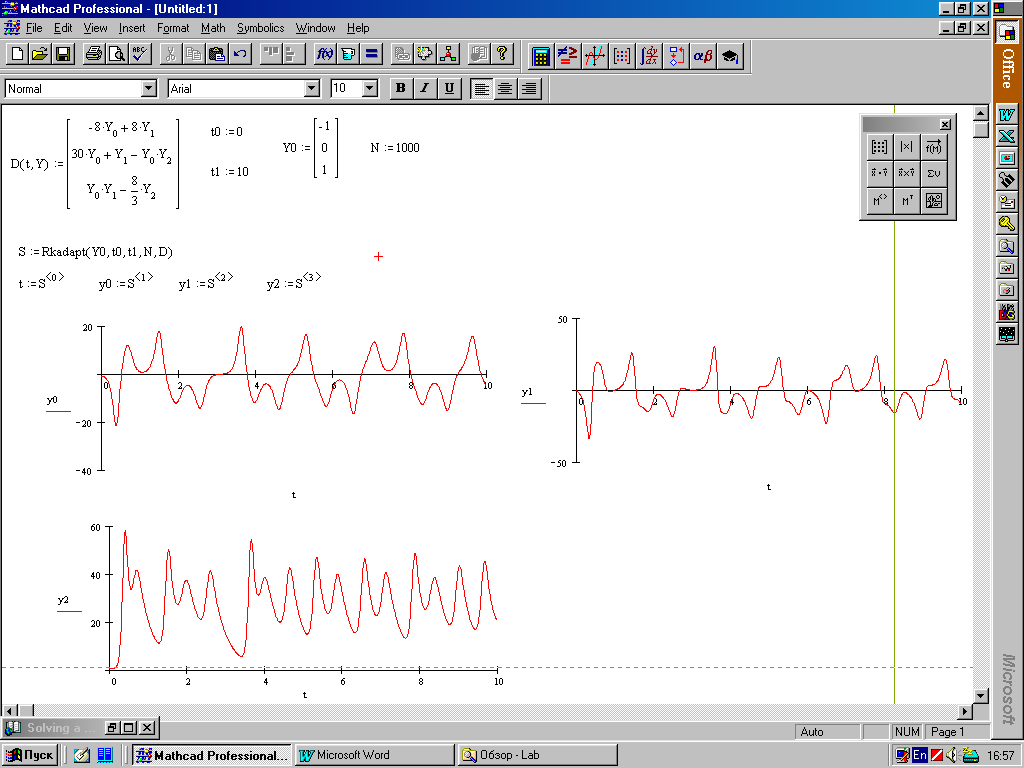 Рис.14. Решение системы обыкновенных дифференциальных уравнений первого порядка с помощью встроенных функций MathCad 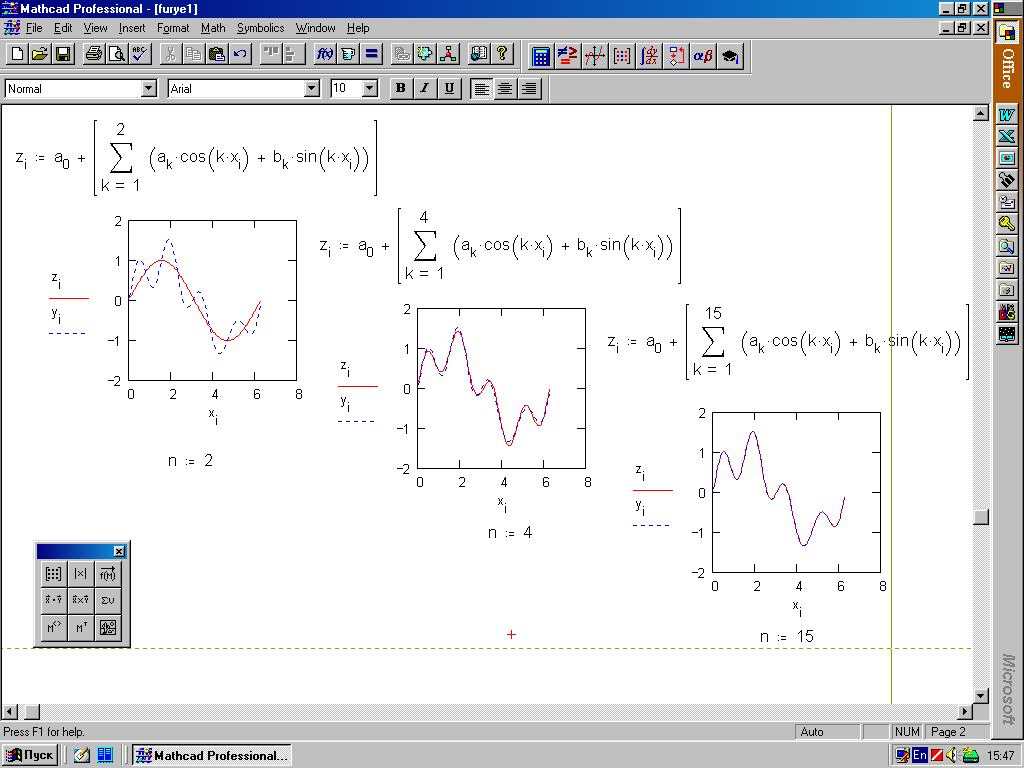 Рис.15 Вид графика приближающей функции в зависимости от значения n |
