Ххх. Учебное пособие Капранов Б. И., Коротков М. М., Короткова И. А. Издательство Томского политехничекого университета 2004
 Скачать 4.67 Mb.
|
4.2. Акустический тракт эхо-методаАкустический тракт – это путь ультразвука от излучателя до объекта, отражающего или рассеивающего ультразвук, и затем к приемнику колебаний. Формулы акустического тракта определяют ослабление амплитуды сигнала на этом пути. При наличии или отсутствии дефектов. Естественные дефекты могут иметь самую различную форму (объемные, плоскостные), величину, ориентацию (вертикальную, горизонтальную и т.д.), акустические свойства, которые заранее не известны. Поэтому формулы выводят для моделей дефектов полых отражателей простой геометрической формы: бесконечно тонкого диска, сферы, цилиндра, бесконечно тонкой полосы, плоскости и т.д. При экспериментах эти модели заменяют искусственными отражателями в виде плоскодонного отверстия, отверстием со сферическим дном, боковым цилиндрическим отверстием, полоской (рис. 14), так как они наиболее соответствуют основным типам реальных дефектов (рис. 15).  Рис. 14. Физические модели дефектов модели дефектов.  Рис. 15. Реальные модели физических дефектов Амплитуды эхо – сигналов от дефектов мало отличаются, если размеры дефектов больше длины волны ультразвука. Обычно при выводе формул акустического тракта не учитывают затухание ультразвука. Поэтому в формулы добавляют множитель  , где  - коэффициент затухания, х – расстояние от преобразователя до отражателя.Отражение от диска или отверстия с плоским дном. Для случая, когда один и тот же преобразователь работает на излучение и прием (рис. 16), получают следующее выражение для давления на приемнике 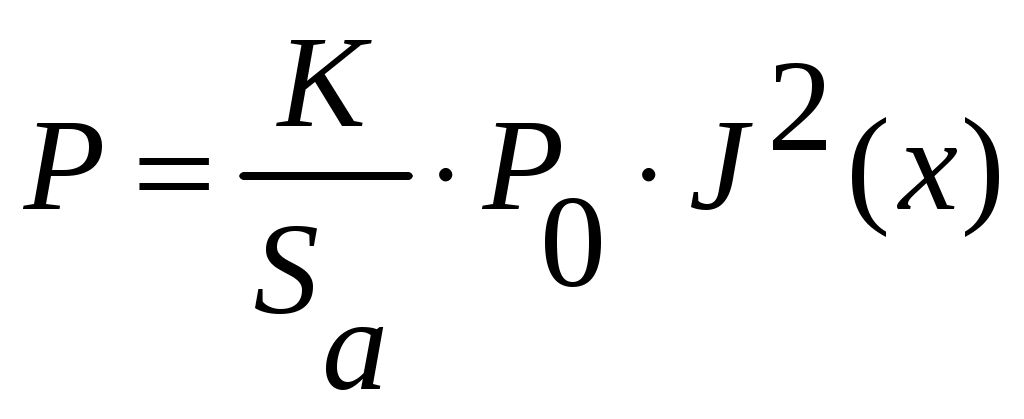 или 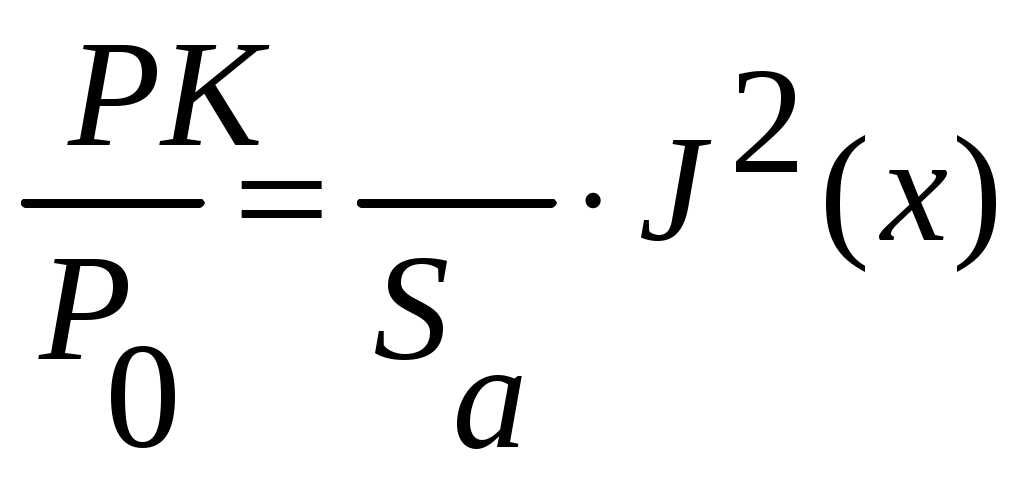 где:  - давление на приемнике; - площадь преобразователя ( ); - коэффициент, определяющий отражающую способность дефекта; - давление, создаваемое излучателем; - функция, описывающая пространственное распределение поля излучателя. Рис. 16. К расчету акустического тракта. Рассматривая дефект в виде произвольной площадки площадью  получим для соотношение ,где:  - коэффициент отражения волны на границе сталь-воздух; - площадь дефекта (для диска  )Отсюда, давление на приемнике будет определяться соотношением 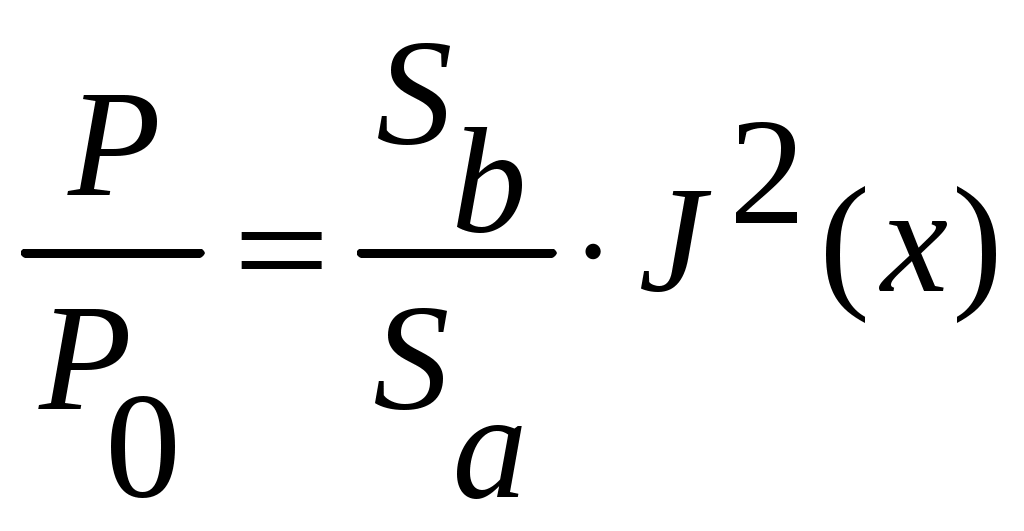 Для дискового преобразователя в ближней зоне функция имеет максимумы и минимумы и принимает значения от 14 (рис. 17). В дальней зоне монотонно уменьшается по закону ,где:  - длина волны;х – расстояние от преобразователя до дефекта.  Рис. 17. Удельная мощность. Полное давление на приемнике определяется как интеграл по всей площади отражающего диска, т.е.  Для полого диска R1. Если размеры дефекта невелики, но больше длины волны , то функцию  в пределах дефекта можно считать постоянной. Тогда отражательная способность К определяется площадью дефекта . Отсюда запишемдля ближней зоны 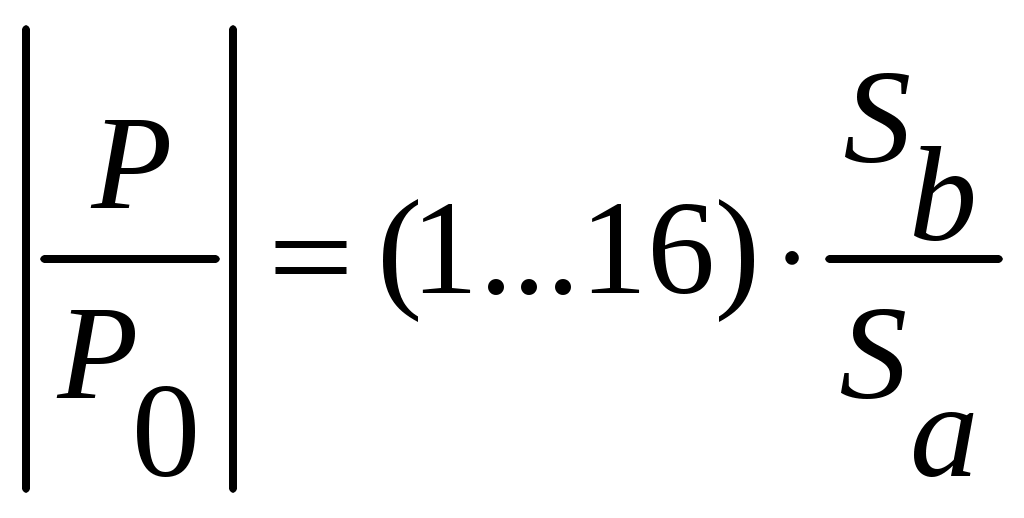 для дальней зоны 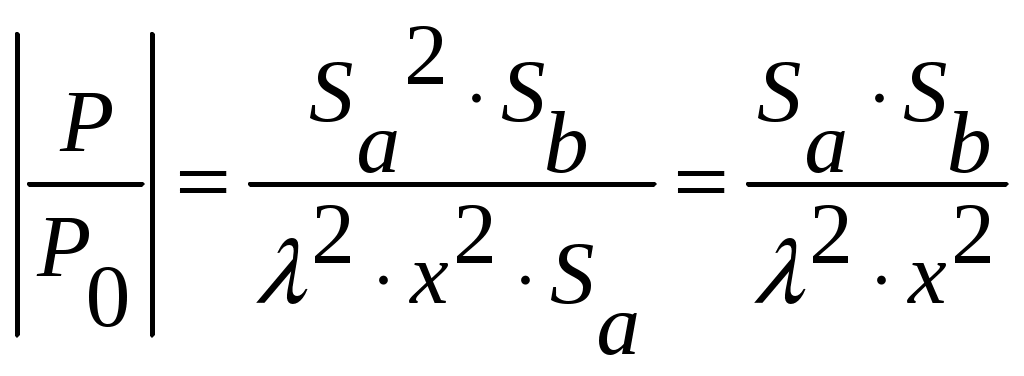 Следовательно, амплитуда отражения от небольшого плоского дефекта не зависит от его формы и пропорциональна его площади. Отношение площади дефекта к квадрату длины волны обозначают через 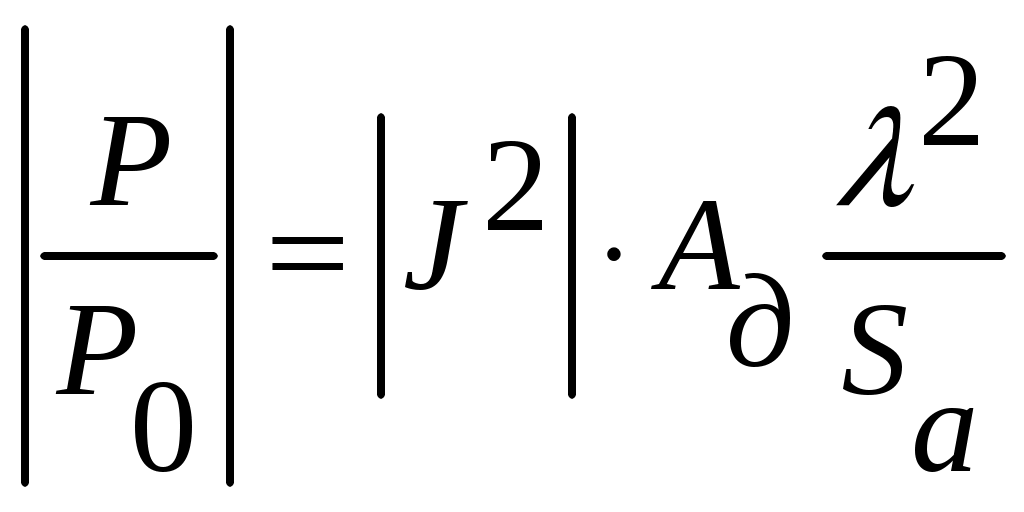 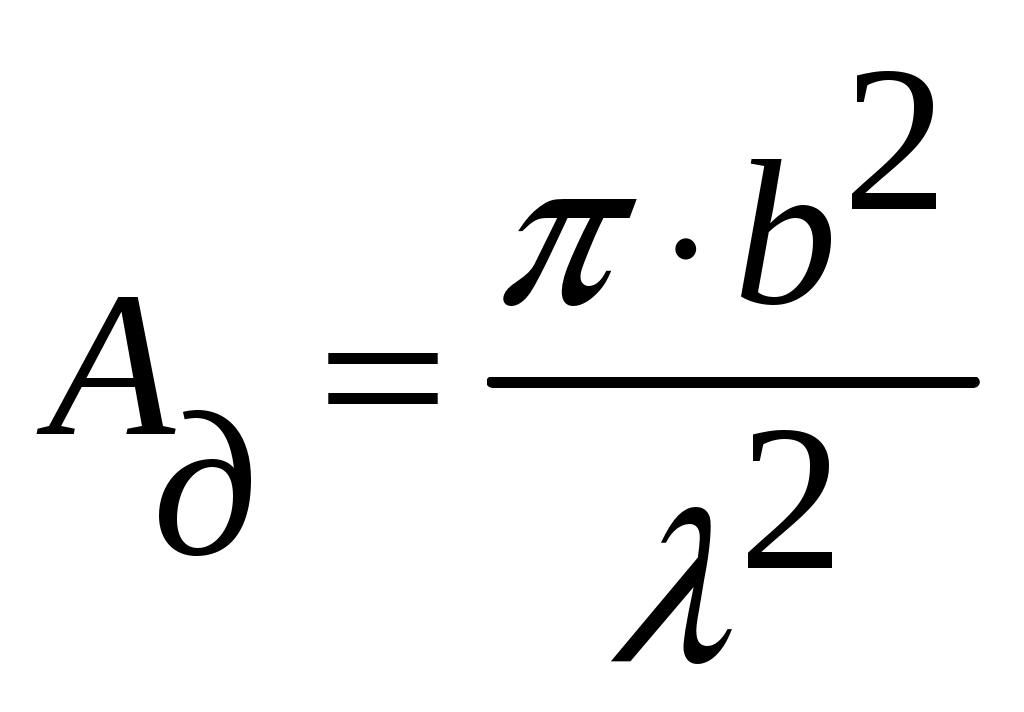. Коэффициент  характеризует отражающую способность дефекта. Через него выражают эхо – сигнал  Когда дефект значительно меньше длины волны, то зависимость отражательной способности от диаметра дефекта и длины волны имеет другой характер 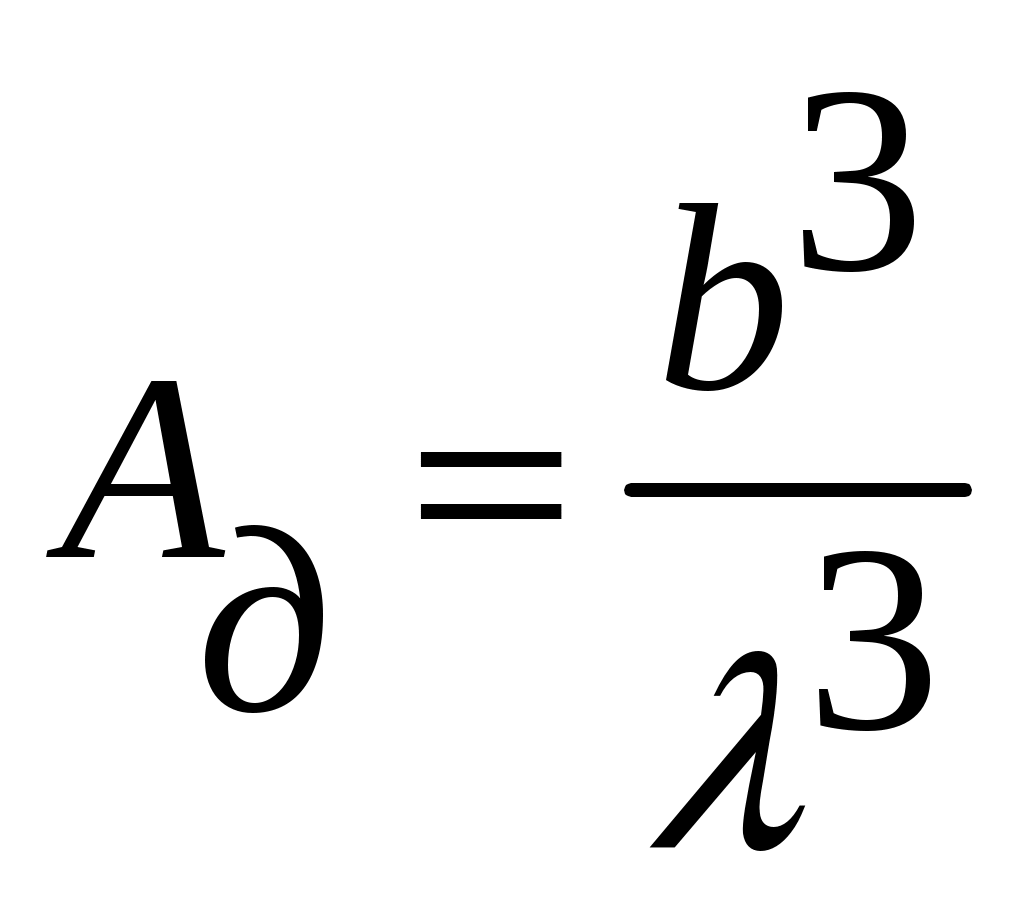 Экспериментально трудно проверить зависимость от относительного размера дефекта, так как трдно изготовить модель дискообразного дефекта не имеющего входного отверстия. Зависимость от отношения  для плоскодонного отверстия имеет вид (рис. 3.18) Рис. 18. Отражательная способность дефекта. В расчетах предполагалось постоянство функции на всей площади дефекта.Если площадь отражающего диска (плоскодонного отверстия) увеличить и приблизить к площади преобразователя, то изменением функции на поверхности дефекта пренебречь нельзя. В результате уменьшения функции от центра к периферии отражателя амплитуда сигнала возрастает с ростом дефекта медленнее, чем по закону  . Когда размер дефекта достигает, а затем превосходит размер преобразователя, возможны две закономерности изменения амплитуды эхо – сигнала.Если отражатель находится в ближней зоне, то амплитуда эхо – сигнала от него возрастает и приближается к амплитуде донного сигнала (дно находится на расстоянии, равном расстоянию до дефекта, дефект становиться большим и превращается в дно). Если же отражатель находится в дальней зоне преобразователя, то амплитуда эхо – сигнала от него может превзойти амплитуду донного сигнала, испытать одну или две осцилляции и только после этого принять значение, равное амплитуде донного сигнала. Такая зависимость объясняется тем, что отражающий диск подобен вторичному излучателю, имеющему свою ближнюю и дальнюю зоны. Когда отражающий диск больше преобразователя, диск может находиться в его дальней зоне, а преобразователь – в ближней зоне отражающего диска. Это и служит причиной осцилляций эхо – сигнала. При диаметре диска  преобразователь находится на границе ближней зоны отражателя и это положение соответствует максимуму амплитуды отраженного сигнала.Анализ выражения показывает, что величина  может быть представлена как функция двух безразмерных параметров:Расстояния от преобразователя до отражателя, отнесенного к длине ближней зоны (  );Отношения диаметра отражающего диска к диаметру преобразователя (  ).В самом деле заменяя путем подстановки и преобразований можно получить следующее выражение 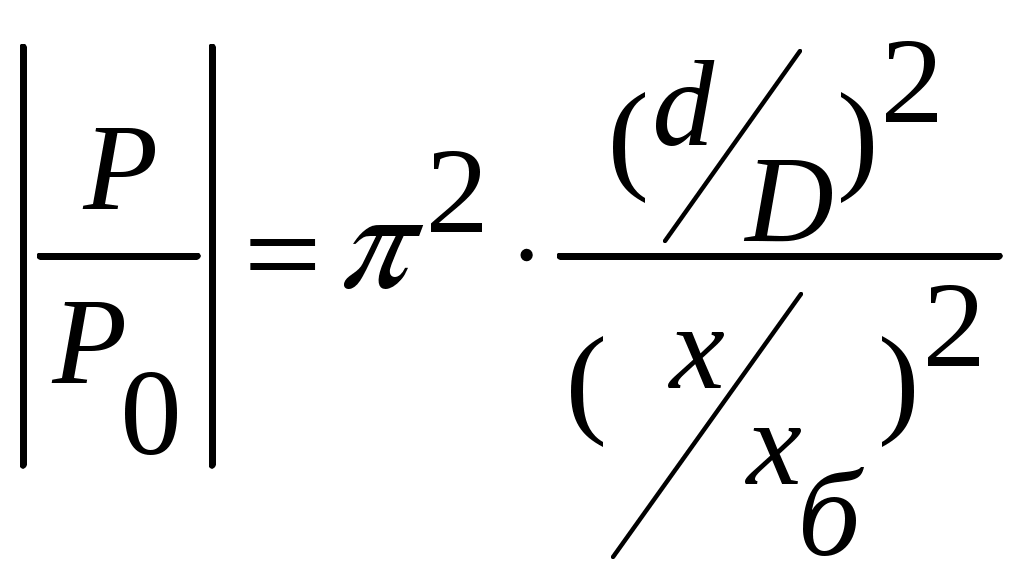 На основе этого соотношения для расчета амплитуды отражения от диска или плоскодонного отверстия в широком диапазоне расстояний и диаметров можно построить семейство безразмерных кривых амплитуда – расстояние – диаметр (АРД –диаграмма). В этой диаграмме по оси абсцисс откладывают относительное расстояние до дефекта в единицах длин ближней зоны, по оси ординат откладывают амплитуду отраженного сигнала в отрицательных децибелах (или относительных единицах) (рис. 19). В таких диаграммах учитывается также экспоненциальное ослабление амплитуды отраженного сигнала за счет затухания  Рис. 19 |