курсовая работа. Учебное пособие по дисциплине технология разработки программного обеспечения специальность Программирование в компьютерных системах

• Название: Учебное пособие по дисциплине технология разработки программного обеспечения специальность Программирование в компьютерных системах
• Анкор: курсовая работа
• Дата: 08.01.2023
• Размер: 7.57 Mb.
• Имя файла: 2_5397965015586183048-7.doc
• Тип: Учебное пособие; #877236
• страница: 20 из 30

Глава 14. Функциональное тестирование ПО
Функциональное тестирование, основанное на принципе «чёрного ящика», может применяться как на уровне программных модулей, так .и на уровне программной системы.
1. Особенности тестирования «чёрного ящика»
Тестирование «чёрного ящика» (функциональное тестирование) позволяет получить комбинации входных данных, обеспечивающих полную проверку всех функциональных требований к программе. Программное тестирование здесь рассматривается как «чёрный ящик», чьё поведение можно определить только исследованием его входов и соответствующих выходов. При таком подходе желательно иметь:

• 
  набор, образуемый такими входными данными, которые приводят к аномалиям поведения программы (назовём его IT);
  
• 
  набор, образуемый такими входными данными, которые демонстрируют дефекты программы (назовём его OT).
  

Как показано на рисунке 1, любой способ тестирования «чёрного ящика» должен:

• 
  выявить такие входные данные, которые с высокой вероятностью принадлежат набору IT;
  
• 
  сформулировать такие ожидаемые результаты, которые с высокой вероятностью являются элементами набора OT.
  

Во многих случаях определение таких текстовых вариантов основывается на предыдущем опыте инженеров тестирования. Они используют своё значение и понимание области определения для идентификации тестовых вариантов, которые эффективно обнаруживают дефекты. Тем не менее систематический подход к выявлению текстовых данных может использоваться как полезное дополнение к эвристическому знанию.



Выходные данные,

приводящие к аномалиям

поведения
Выходные данные,

выявляющие наличие

дефектов
Рис. 1. Тестирование «чёрного ящика»

Принцип «чёрного ящика» не альтернативен принципу «белого ящика». Скорее это дополняющий подход, который обнаруживает другой класс ошибок.

Тестирование «чёрного ящика» обеспечивает поиск следующих категорий ошибок:

1. 
   некорректных или отсутствующих функций;
   
2. 
   ошибок интерфейса;
   
3. 
   ошибок во внешних структурах данных или в доступе к внешней базе данных;
   
4. 
   ошибок характеристик (необходимая ёмкость памяти);
   
5. 
   ошибок инициализации и завершения;
   

Подобные категории ошибок способами «белого ящика» не выявляются.

В отличие от тестирования «белого ящика», которое выполняется на ранней стадии процесса тестирования, тестирование «чёрного ящика» применяют на поздних стадиях тестирования. При тестировании «чёрного ящика» пренебрегают управляющей структурой программы. Здесь внимание концентрируется на информационной области определения программной системы.

Техника «чёрного ящика» ориентированна на решении следующих задач:

• 
  сокращение необходимого количества тестовых вариантов (из-за проверки не статических, а динамических аспектов системы);
  
• 
  выявление классов ошибок, а не отдельных ошибок;
  

2. Способ разбиения по эквивалентности
Разбиение по эквивалентности − самый популярный способ тестирования «чёрного ящика». В этом способе входная область данных программы делится на классы эквивалентности. Для каждого класса эквивалентности разрабатывается один тестовый вариант. Класс эквивалентности − набор данных с общими свойствами. Обрабатывая разные элементы класса, программа должна вести себя одинаково. Иначе говоря, при обработке любого набора из класса эквивалентности в программе задействуется один и тот же набор операторов (и связей между ними). На рис.2. каждый класс эквивалентности показан эллипсом. Здесь выделены входные классы эквивалентности допустимых и недопустимых исходных данных, а также классы результатов. Классы эквивалентности могут быть определены по спецификации на программу.

Классы эквивалентности исходных данных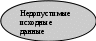





Программное изделие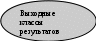


Рис. 2. Разбиение по эквивалентности
Например, если спецификация задаёт в качестве допустимых входных величин 5-разрядные целые числа в диапазоне 15 000…70 000, то класс эквивалентности допустимых ИД (исходных данных) включает величины от 15 000 до

70 000, а два класса эквивалентности недопустимых ИД составляют:

• 
  числа меньшие, чем 15 000;
  
• 
  Числа большие, чем 70 000;
  

Класс эквивалентности включает множество значений данных, допустимых или недопустимых по условиям ввода.

Условие ввода может задавать:

1. 
   определённое значение;
   
2. 
   диапазон значений;
   
3. 
   множество конкретных величин;
   
4. 
   булево условие;
   

Сформулируем правила формирования классов эквивалентности.

1. Если условие ввода задаёт диапазон n…m, то определяются один допустимый и два недопустимых класса эквивалентности:

• 
  V_Class={n…m} − допустимый класс эквивалентности;
  
• 
  Inv_Class1={x|для любого x: x<n} − первый недопустимый класс эквивалентности;
  
• 
  Inv_Class2={y|для любогоy: y>m} − второй недопустимый класс эквивалентности;
  

2. Если условие ввода задаёт конкретное значение а, то определяются один допустимый и два недопустимых класса эквивалентности:

• 
  V_Class={а};
  
• 
  Inv_Class1={x|для любого x: x<a};
  
• 
  Inv_Class2={y|для любогоy: y>a};
  

3. Если условие ввода задаёт множество значений {а,b,c},то определяются один допустимый и один недопустимый класс эквивалентности:

• 
  V_Class={а,b,c};
  
• 
  Inv_Class={x|для любого x:(x≠ a)&(x≠ b)&(x≠ c)}.
  

4. Если условие ввода задаёт булево значение, например true, то определяются один допустимый и один недопустимый класс эквивалентности:

• 
  V_Class={ true};
  
• 
  Inv_Class={false}.
  

После построения классов эквивалентности разрабатываются тестовые варианты. Тестовый вариант выбирается так, чтобы проверить сразу наибольшее количество свойств класса эквивалентности.
3. Способ анализа граничных значений
Как правило, большая часть ошибок происходит на границах области ввода, а не на центре. Анализ граничных значений заключается в получении тестовых вариантов, которые анализируют граничные значения. Данный способ тестирования дополняет способ разбиения по эквивалентности:

1. 
   тестовые варианты создаются для проверки только рёбер классов эквивалентности;
   
2. 
   при создании тестовых вариантов учитывают не только условия ввода, но и область ввода.
   

Сформулируем правила анализа граничных значений.

1. Если условие ввода задаёт диапазон n…m, то тестовые варианты должны быть построены:

• 
  для значений nиm;
  
• 
  для значений чуть левееnи чуть правее m на числовой оси.
  

Например, если задан входной диапазон -1,0…+1,0, то создаются тесты для значений -1,0, +1,0, -1,001, +1,001.

2. Если условие ввода задаёт множество значений, то создаются тестовые варианты:

• 
  для проверки минимального и максимального из значений;
  
• 
  для значений чуть меньше минимума и чуть больше максимума.
  

Так, если входной файл может содержать от 1 до 255 записей, то создаются тесты для 0, 1, 255, 256 записей.

3. Правила 1 и 2 применяются к условиям области вывода.

Рассмотрим пример, когда в программе требуется выводить таблицу значений. Количество строк и столбцов в таблице меняется. Задаётся тестовый вариант для минимального вывода (по объёму таблицы), а также тестовый вариант для максимального вывода (по объёму таблицы).

4. Если внутренние структуры данных программы имеют предписанные границы, то разрабатываются тестовые варианты, проверяющие эти структуры на их границах.

5. Если входные или выходные данные программы являются упорядоченными множествами (например, последовательным файлом, линейным списком, таблицей), то надо тестировать обработку первого и последнего элементов этих множеств.

Большинство разработчиков используют этот способ интуитивно. При применении описанных правил тестирования границ будет более полным, в связи, с чем возрастёт вероятность обнаружения ошибок.

Пример. Рассмотрим применение способов разбиения по эквивалентности и анализа граничных значений на конкретном примере. Положим, что нужно протестировать программу бинарного поиска. Нам известна спецификацияэтой программы. Поиск выполняется в массиве элементов М, возвращается индекс Iэлемента массива, значение которого соответствует ключу поиска Key.

Пред-условия:

1. 
   массив должен быть упорядочен;
   
2. 
   массив должен иметь не менее одного элемента;
   
3. 
   нижняя граница массива (индекс) должна быть меньше или равна его верхней границе;
   

Пост-условия:

1. 
   если элемент найден, то флаг Result=True, значение I − номер элемента;
   
2. 
   если элемент не найден, то флаг Result=False, значение I не определено.
   

Для формирования классов эквивалентности (и их рёбер) надо произвести разбиение области ИД − построить дерево разбиений. Листья дерева разбиений дадут нам искомые классы эквивалентности. Определим стратегию разбиения. На первом уровне будем анализировать выполнимость предусловий, на втором − выполнимость постусловий. На третьем уровне можно анализировать специальные требования, полученные из практики разработчика. В нашем примере мы знаем, что входной массив должен быть упорядочен. Обработка упорядоченных наборов из чётного и нечётного количества элементов может выполняться по-разному. Кроме того, принято выделять специальный случай одноэлементного массива. Следовательно, на уровне специальных требований возможны следующие эквивалентные разбиения:

1. 
   массив из одного элемента;
   
2. 
   массив из чётного количества элементов;
   
3. 
   массив из нечётного количества элементов, большего единицы.
   

Наконец, на последнем, 4-м уровне критерием разбиения может быть анализ рёбер классов эквивалентности. Очевидно, возможны следующие варианты:

1. 
   работа с первым элементом массива;
   
2. 
   работа с последним элементом массив;
   
3. 
   работа с промежуточным (ни с первым, ни с последним) элементом массива;
   

Структура дерева разбиений приведена на рис. 3.

Это дерево имеет 11 листьев. Каждый лист задаёт отдельный тестовый вариант. Покажем тестовые варианты, основанные на проведённых разбиениях.

Тестовый вариант 1 (единичный массив, элемент найден) ТВ1:

ИД: М=15; Key=15.

ОЖ.РЕЗ.: Result=True; I=1.

Тестовый вариант 2 (чётный массив, найден 1-й элемент) ТВ2:

ИД: М=15,20,25,30,35,40; Key=15.

ОЖ.РЕЗ.: Result=True; I=1.

Тестовый вариант 3 (чётный массив, найден последний элемент) ТВ3:

ИД: М=15,20,25,30,35,40; Key=40.

ОЖ.РЕЗ.: Result=True; I=6.

Тестовый вариант 4 (чётный массив, найден промежуточный элемент) ТВ4:

ИД: М=15,20,25,30,35,40; Key=25.

ОЖ.РЕЗ.: Result=True; I=3.

Тестовый вариант 5 (нечётный массив, найден 1-й элемент) ТВ5:

ИД: М=15,20,25,30,35,40,45; Key=15.

ОЖ.РЕЗ.: Result=True; I=1.

Тестовый вариант 6 (нечётный массив, найден последний элемент) ТВ6:

ИД: М=15,20,25,30,35,40,45; Key=45.

ОЖ.РЕЗ.: Result=True; I=7.

Тестовый вариант 7 (нечётный массив, найден промежуточный элемент) ТВ7:

ИД: М=15,20,25,30,35,40,45; Key=30.

ОЖ.РЕЗ.: Result=True; I=4.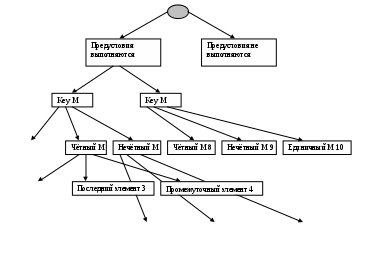


Единичный М1

^{Первый элемент 2}

Первый элемент 5

Последний элемент 6


Промежуточный элемент 7


Предусловия
Постусловия


Специальные требования

Граничные рёбра
Рис.3. Дерево разбиений области исходных данных бинарного поиска
Тестовый вариант 8 (чётный массив, не найден элемент) ТВ8:

ИД: М=15,20,25,30,35,40; Key=23.

ОЖ.РЕЗ.: Result= False; I=?.

Тестовый вариант 9 (нечётный массив, не найден элемент) ТВ9:

ИД: М=15,20,25,30,35,40,45; Key=24.

ОЖ.РЕЗ.: Result= False; I=?.

Тестовый вариант 10 (единичный массив, не найден элемент) ТВ10:

ИД: М=15; Key=0.

ОЖ.РЕЗ.: Result= False; I=?.

Тестовый вариант 11 (нарушены предусловия) ТВ11:

ИД: М=15,10,5,25,20,40,35; Key=35.

ОЖ.РЕЗ.: Аварийное донесение. Массив не упорядочен.
4. Способ диаграмм причин-следствий
Диаграммы причинно-следственных связей – способ проектирования тестовых вариантов, который обеспечивает формальную запись логических условий и соответствующих действий . Используется автоматный подход к решению задачи.

Шаги способа:

1. 
   для каждого модуля перечисляются причины (условия ввода или классы эквивалентности условий ввода) и следствия (действия или условия ввода). Каждой причине и следствию присваивается свой идентификатор;
   
2. 
   разрабатывается граф причинно-следственных связей4
   
3. 
   граф преобразуется в таблицу решений;
   
4. 
   столбцы таблицы решений преобразуются в тестовые варианты.
   

Изобразим базовые символы для записи графов причин и следствий (cause-effect graphs).

Обозначения. Сделаем предварительные замечания:

1. 
   причины будем обозначать символами c_i , а следствия – символами e_i;
   
2. 
   каждый узел графа может находиться в состоянии 0 или 1 (0 – состояние отсутствует, 1 – состояние присутствует).
   

Функция тождество (рис. 4) устанавливает, что если значение c_iесть 1, то и значение e_iесть 1; в противном случае значение e_iесть 0.


Рис. 4. Функция тождество

Функция не (рис. 5) устанавливает, что если значение c₁есть 1, то значение е₁ есть 0, в противном случае значение е₁ есть 1.





Рис. 5. Функция не
Функция или (рис. 6) устанавливает, что если c₁ или c₂ есть 1, то е₁ есть 1, в противном случае е₁ есть 0.








V




Рис. 6. Функция или

Функция или (рис. 7) устанавливает, что если c₁ и c₂ есть 1, то е₁ есть 1, в противном случае е₁ есть 0.

Часто определённые комбинации причин невозможны из-за синтаксических или внешних ограничений. Используются перечисленные ниже обозначения ограничений.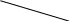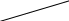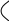


Рис. 7. Функция и
Ограничение Е (исключает, Exclusive, рис. 8) устанавливает, что Е должно быть истинным, если хотя бы одна из причин – а или b – принимает значение 1 (а и b не могут принимать значение 1одновременно).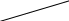







Е




Рис. 8. Ограничение Е (исключает, Exclusive)

О граничение I (включает, Inclusive, рис. 9) устанавливает, что по крайней мере одна из величин а, b или с, всегда должна быть равной 1(а, bи с не могут принимать значение 0 одновременно

I

Рис. 9. Ограничение I (включает, Inclusive)

О 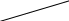граничение O (одно и только одно, Only one, рис. 10) устанавливает, что одна и только одна из величин а или b должна быть равна 1.

О
Рис. 10. Ограничение О (одно и только одно, Only one)
Ограничение R (требует, Requires, рис. 11) устанавливает, что если а принимает значение 1, то и b должна принимать значение 1 (нельзя, чтобы а было равно 1, а б – 0).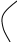



R

Рис. 11. Ограничение R (требует, Requires)
Часто возникает необходимость в ограничениях для следствий.

Ограничение М (скрывает, Masks, рис. 12) устанавливает, что если следствие а имеет значение 1, то следствие b должно принять значение 0.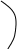










Рис. 12. Ограничение М (скрывает, Masks)

Пример

Для иллюстрации использования способа рассмотрим пример, когда программа выполняет расчёт оплаты за электричество по среднему или переменному тарифу.

При расчёте по среднему тарифу:

• 
  при месячном потреблении энергии меньшем, чем 100 кВт/ч, выставляется фиксированная сумма;
  
• 
  при потреблении энергии большем или равном 100 кВт/ч применяется процедура А планирования расчёта;
  

При расчёте по переменному тарифу:

• 
  при месячном потреблении энергии меньшем, чем 100 кВт/ч, применяется процедура А планирования расчёта;
  
• 
  при потреблении энергии большем или равном 100 кВт/ч применяется процедура В планирования расчёта;
  

Шаг 1. Причинами являются:

1. 
   расчёт по среднему тарифу;
   
2. 
   расчёт по переменному тарифу;
   
3. 
   месячное потребление электроэнергии меньшее, чем 100 кВт/ч;
   
4. 
   месячное потребление электроэнергии большее или равное 100 кВт/ч.
   

На основании различных комбинаций причин можно перечислить следующие следствия:

• 
  101 – минимальная месячная стоимость;
  
• 
  102 – процедура А планирования расчёта;
  
• 
  103 – процедура В планирования расчёта;
  

Шаг 2. Разработка графа причинно-следственных связей (рис.13).

Узлы причин перечислим по вертикали у левого края рисунка, а узлы следствий – у правого края рисунка. Для следствия 102 возникает необходимость введения вторичных причин – 11 и 12, – их размещаем в центральной части рисунка.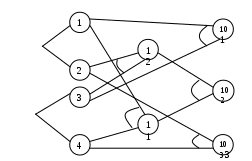


Е
V
О


Рис. 13. Граф причинно-следственных связей
Шаг 3. Генерация таблицы решений. При генерации причины рассматриваются как условия, а следствия – как действия.

Порядок генерации.

1. 
   Выбирается некоторое следствие, которое должно быть в состоянии «1».
   
2. 
   Находятся все комбинации причин (с учётом ограничений), которые устанавливают это следствие в состояние «1». Для этого из следствия прокладывается обратная трасса через граф.
   
3. 
   Для каждой комбинации причин, приводящих следствие в состояние «1»,
   

строится один столбец.

4. 
   Для каждой комбинации причин доопределяются состояния всех других следствий. Они помещаются в тот же столбец таблицы решений.
   
5. 
   Действия 1-4 повторяются для всех следствий графа.
   

Таблица решений для нашего примера показана в табл. 1.

Шаг 4. Преобразование каждого столбца таблицы в тестовый вариант. В нашем примере таких вариантов четыре.

Тестовый вариант 1 (столбец 1) ТВ1:

ИД: расчёт по среднему тарифу; месячное потребление электроэнергии 75 кВт/ч.

ОЖ.РЕЗ.: минимальная месячная стоимость.

Тестовый вариант 2 (столбец 2) ТВ2:

ИД: расчёт по переменному тарифу; месячное потребление электроэнергии 90 кВт/ч.

ОЖ.РЕЗ.: процедура А планирования расчёта.

Тестовый вариант 3 (столбец 3) ТВ3:

ИД: расчёт по среднему тарифу; месячное потребление электроэнергии 100 кВт/ч.

ОЖ.РЕЗ.: процедура В планирования расчёта.

Тестовый вариант 4 (столбец 4) ТВ4:

ИД: расчёт по переменному тарифу; месячное потребление электроэнергии 100 кВт/ч.

ОЖ.РЕЗ.: процедура В планирования расчёта.
Табл. 1. Таблица решений для расчёта оплаты за электричество

Номера столбцов→			1	2	3	4
Условия	Причины	1	1	0	1	0
		2	0	1	0	1
		3	1	1	0	0
		4	0	0	1	1
	Вторичные причины	11	0	0	1	0
		12	0	1	0	0
Действия	Следствия	101	1	0	0	0
		102	0	1	1	0
		103	0	0	0	1

Контрольные вопросы

1. 
   Каковы особенности тестирования методом «чёрного ящика»?
   
2. 
   Какие категории ошибок выявляют тестирования методом «чёрного ящика»?
   
3. 
   Какие достоинства имеет тестирования методом «чёрного ящика»?
   
4. 
   Поясните суть способа разбиения по эквивалентности?
   
5. 
   Что такое класс эквивалентности?
   
6. 
   Что может задавать условие ввода?
   
7. 
   Какие правила формирования классов эквивалентности вы знаете?
   
8. 
   Как выбирается тестовый вариант при тестировании по способу разбиения по эквивалентности?
   
9. 
   Поясните суть способа анализа граничных значений.
   
10. 
    Чем способ анализа граничных значений отличается от разбиения по эквивалентности?
    
11. 
    Поясните правила анализа граничных значений.
    
12. 
    Что такое дерево разбиений? Каковы его особенности?
    
13. 
    В чём суть способа диаграмм причин-следствий?
    
14. 
    Что такое причина?
    
15. 
    Что такое следствие?
    
16. 
    Дайте общую характеристику графа причинно-следственных отношений.
    
17. 
    Какие функции используются в графе причин и следствий?
    
18. 
    Какие ограничения используются в графе причин и следствий?
    
19. 
    Поясните шаги способа диаграмм причин-следствий.
    
20. 
    Какую структуру имеет таблица решений в способе диаграмм причин-следствий?
    
21. 
    Как таблица решений преобразуется в тестовые варианты?