Учебное пособие по дисциплине. Учебное пособие в оронеж 2006 Воронежский государственный технический университет Е. И. Воробьева

• Название: Учебное пособие в оронеж 2006 Воронежский государственный технический университет Е. И. Воробьева
• Дата: 17.11.2022
• Размер: 5.5 Mb.
• Имя файла: Учебное пособие по дисциплине.doc
• Тип: Учебное пособие; #792926
• страница: 2 из 21

ВВЕДЕНИЕ

Современная жизнь характеризуется повышенной деловой активностью населения. Любая сколь угодно полезная информация не может быть использована, если отсутствует каналы связи для ее передачи и приема. Сама по себе информация не имеет ценности, если ею нельзя воспользоваться.

Два крупных достижения в области фундаментальной науки – общая теория связи и достижения микроэлектроники – позволили совершить научно-техническую революцию в области связи.

Необходимость обладания информацией в определенное время, увеличение объема этой информации и уменьшение сроков ее доставки до адресата, возможность ее оперативной передачи и приема обусловили широкое внедрение спутниковых, волоконно-оптических систем связи, систем с шумоподобными сигналами, подвижной радиосвязи. Для предоставления современных услуг связи деловым потребителям недостаточно сети обычной телефонной связи. Сегодня стало актуально и экономически выгодно пользоваться сотовым телефоном или спутниковым терминалом.

Для правильного понимания функционирования действующих и перспективных систем передачи информации специалисту в области связи, а тем более специалисту в области защиты информации, передаваемой по каналам связи, необходимо знать основные положения теории сигналов, сообщений, информации, модуляции, оптимального приема и помехоустойчивого кодирования, принципы построения многоканальных систем передачи, высокоскоростных модемов, сжатия сообщений и многое другое.

Передача информации ведущаяся в условиях воздействия сильных и разнообразных помех, в том числе и преднамеренных, поэтому системы связи должны обладать высокой помехоустойчивостью, а также высокой эффективностью при относительной простоте технической реализации и эксплуатации. Это значит, что надо передавать наибольшее количество информации наиболее экономичным способом в заданное время. Последнее достигается благодаря использованию наиболее современных способов передачи (кодирования и модуляции) и приема (декодирования и демодуляции). Перечисленные вопросы подробно излагаются в данном учебном пособии.

Кроме того, в пособии рассмотрены вопросы организации и функционирования систем электросвязи, таких как: системы телефонной вязи, коротковолновые и ультракоротковолновые системы связи, системы подвижной радиосвязи общего пользования, спутниковые системы связи.

Также рассмотрены вопросы построения сетей передачи информации и системы коммуникации. Даются характеристики техническим средствам телекоммуникационных систем.

В основу предполагаемого пособия положен опыт преподавания дисциплин «Теория информации» и «Системы и сети передачи информации», читаемых в Воронежском государственном техническом университете для студентов, обучающихся по направлению «Информационная безопасность». Авторы благодарят Потапова Николая Юрьевича за помощь в оформлении материала учебного пособия.

1.СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ. СПОСОБЫ ПРЕДСТАВЛЕНИЯ И ПРЕОБРАЗОВАНИЯ СООБЩЕНИЙ, СИГНАЛОВ И ПОМЕХ.

1.1 Общие сведения о системах связи

1.1.1 Информация. Сообщение. Сигнал

Информация наряду с материей и энергией является первичным понятием нашего мира и поэтому в строгом смысле не может быть определена. Можно лишь перечислить ее основные свойства, например такие как:

1. 
   информация приносит сведения, об окружающем мире которых в рассматриваемой точке не было до ее получения;
   
2. 
   информация не материальна, но она проявляется в форме материальных носителей дискретных знаков или первичных сигналах;
   
3. 
   знаки и первичные сигналы несут информацию только для получателя способного распознать.
   

Вместе с тем слово информация является одним из тех терминов, которые достаточно часто встречаются не только в научных трудах специального характера, но и во множестве обиходных ситуаций и являются интуитивно понятными каждому человеку. При этом в узком практическом смысле под информацией обычно понимают совокупность сведений об окружающем мире являющихся объектом хранения, передачи и преобразования. Знаки или первичные сигналы, организованные в последовательности несут информацию не потому, что они повторяют объекты реального времени, а по общественной договоренности об однозначной связи знаков и объектов, например: предметы и слова для их обозначения. Кроме того, первичные сигналы могут быть порождены естественными законами реального мира, например: напряжение на выходе термопары под действием температуры.

Информация, основанная на однозначной связи знаков или сигналов с объектами реального мира, называется семантической или смысловой. Информация, заключенная в характере (порядке и взаимосвязи) следования знаков сообщающей называется синтаксической. Также в общей науке о знаках (семиотики) кроме перечисленных выделяют сигматический и прагматический аспекты информации. В первом случае изучается вопрос о выборе знаков для обозначения объектов реального мира, во втором случае о ценности информации для достижения поставленных целей. Очевидно, что наибольший практический интерес представляют смысловой и семантический и прагматический аспекты. Однако до сих пор не определены объективные количественные критерии меры ценности и полезности информации.

Информация передается, и храниться в виде сообщений. Под сообщением понимают совокупность знаков или первичных сигналов содержащих информацию. Иначе говоря, сообщение - это информация представленная в какой-либо форме. Пример сообщений: текст телеграммы, данные на выходе ЭВМ, речь, музыка и т.д. Для того чтобы сообщение можно было передать получателю, необходимо воспользоваться некоторым физическим процессом, способным с той или иной скоростью распространяться от источника к получателю сообщения. Изменяющийся во времени физический процесс, отражающий передаваемое сообщение называется сигналом.

Сообщения могут быть функциями времени (когда информация представлена в виде первичных сигналов: речь, музыка) и не является ими (когда информация представлена в виде совокупности знаков). Сигнал всегда является функцией времени.

Возможность способа передачи учитывается способом преобразования сообщения в сигнал. В случае электросвязи все виды информации с помощью соответствующих электронных приборов преобразуются в электрические сигналы, отображающие сообщение.

Сигнал – это материально-энергетическая форма представления информации. Другими словами, сигнал – это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение.

Цепь “информация – сообщение – сигнал” – это пример процесса обработки, необходимой там, где находится источник информации. На стороне потребителя информации осуществляется обработка в обратном порядке: “сигнал – сообщение – информация”.

Существует несколько физических характеристик, общих для любого сигнала. Физическая характеристика сигнала – это описание любым способом его свойств.

Сигнал может быть характеризован различными параметрами. Для систем передачи имеют важное значение лишь три основных параметра: время передачи Тс, динамический диапазон изменения мощности сигнала от максимального Рс макс. до минимального Рс мин. значения и ширина полосы частот спектра ∆Fс.

Время передачи сигнала Тс характеризуется тем, что для передачи сигнала, несущего большую информацию, при прочих равных условиях, требуется и большее время.

Динамическим диапазоном характеризуют пределы изменения мощности сигнала. Оценивают динамический диапазон логарифмом отношения крайних значений мощности сигнала Рс макс./Рс мин., т.е.
Dc = 10lg(Рс макс./Рс мин). (1.1)
Полученное при этом значение динамического диапазона выражается в децибелах (дБ).

Третий параметр – ширина полосы спектра частот сигнала ∆Fc также связана с объемом информации, которую несет сигнал. Ширина полосы частот равна разности максимальной и минимальной частотных компонент сигнала:
∆Fc = Fмакс. – Fмин. (1.2)
Необходимая ширина полосы телефонного сигнала, обеспечивающая достаточную разборчивость и воспроизведение тембра речи, составляет от 300 до 3400 Гц, т.е. 3,1 кГц.

В зависимости от того, какие значения могут принимать аргумент (время t) и уровни сигналов их делят на 4 типа:

1) Непрерывный или аналоговый сигналы (рис.1.1). Случайные сигналы этого типа называются непрерывными случайными процессами. Они определены для всех моментов времени и могут принимать все значения из заданного диапазона. Чаще всего физические процессы, порождающие сигналы являются непрерывными. Этим и объясняется второе название сигналов данного типа аналоговый, т.е. аналогичные порождающим процессам.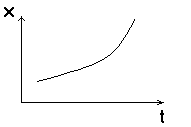


Рис.1.1. Представление аналогового сигнала как непрерывной функции времени
2) Дискретизированный или дискретно непрерывные сигналы (рис.1.2). Случайные сигналы этого типа называют процессами с дискретным временем или непрерывными случайными последовательностями. Они определены лишь в отдельные моменты времени и могут принимать любые значения уровня. Временной интервал Δt между соседними отсчетами называется шагом дискретизации. Часто такие сигналы называют дискретными по времени.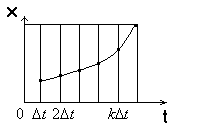


Рис.1.2. Представление дискретного сигнала
3) Дискретные по уровню или квантованные сигналы. Случайные сигналы этого типа называют дискретными случайными процессами. Они определены для всех моментов времени и принимают лишь разрешенные значения уровней отделенные от друг друга на величину шага квантования Δx=x_k+1+x_k (рис.1.3)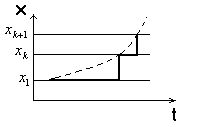


Рис.1.3. Представление квантованного сигнала
4) Дискретные по уровню и по времени сигналы. Случайные сигналы этого типа называют дискретными случайными последовательностями. Они определены лишь в отдельные разрешенные моменты времени и могут принимать лишь разрешенные значения уровней. Такие сигналы называются цифровыми сигналами (рис.1.4).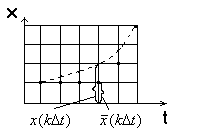


Рис. 1.4. Представление цифрового сигнала

1.1.2 Обобщенная структура систем связи

Современные системы передачи информации (СПИ) представляют собой сложные комплексы, состоящие из различных функционально взаимосвязанных элементов. Эти системы характеризуются не только большим числом элементов, но и иерархичностью структуры, избыточностью, наличием между элементами прямых, обратных и перекрестных связей.

В теории информации широко используют обобщенную модель СПИ (рис. 1.5).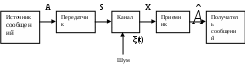



Рис.1.5 Обобщенная модель СПИ.
Здесь под передатчиком понимается устройство, преобразующее сообщения источника А в сигналы S, наиболее соответствующие характеристикам данного канала. Операции, выполняемые передатчиком, могут включать в себя формирование первичного сигнала, модуляцию, кодирование, сжатие данных и т. д.

Приемник производит обработку сигналов X(t)=S(t)+ξ(t) на выходе канала с целью наилучшего воспроизведения (восстановления) переданных сообщений А на приемном конце.

Канал (в узком смысле) — это среда, используемая для передачи сигналов от передатчика к приемнику. Источник сообщений моделируется последовательностью реализаций сообщения А={Ai}ⁿ_i=1, которые могут быть либо дискретными, либо непрерывными.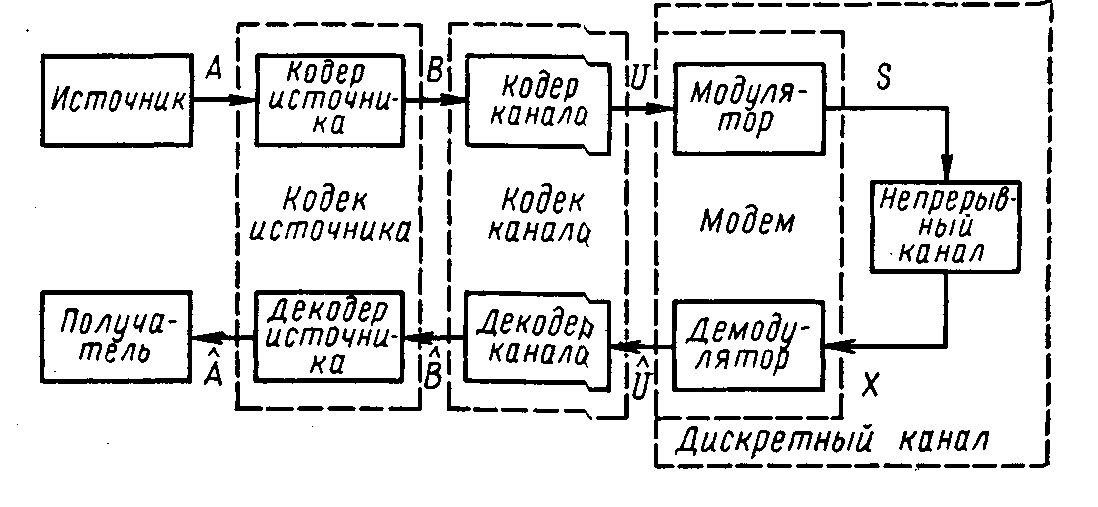



Практически при изучении СПИ удобно операции кодирования и модуляции (соответственно декодирования и демодуляции) разделить и представить модель СПИ в виде развернутой схемы (рис. 1.6). Эта модель также является достаточно общей и может быть использована для представления системы передачи как дискретных, так и непрерывных сообщений.

Рис.1.6 Развернутая обобщенная модель СПИ.
Кодек источника, включающий в себя кодер и декодер, преобразует сообщение в код (кодирование) и код в сообщение (декодирование). В простейшем случае это преобразование заключается в том, что сообщение, вырабатываемое источником, заменяется последовательностью кодовых (обычно двоичных) символов. В более общем случае кодирование осуществляется с учетом статистических свойств передаваемых сообщений с целью уменьшения избыточности источника («сжатия» данных).

Кодек канала, как и кодек источника, содержит устройства кодирования и декодирования. Его назначение – за счет вводимой избыточности уменьшить ошибки, которые возникают при передаче двоичных символов по каналу. Кодек должен согласовывать источник и получатель сообщений с дискретным каналом как по объему алфавита, так и по избыточности. Дискретный канал образуется из непрерывного канала путем включения в него модема. Непрерывный (аналоговый) канал включает в себя линию связи (канал в узком смысле) и высокочастотные блоки передатчика и приемника. В модеме происходят формирование и обработка сигналов, передаваемых по непрерывному каналу, т. е. преобразование кода в сигнал и обратно. Формирование сигнала обычно осуществляется с помощью модуляции. В СПИ, в которых, используются мощные коды с избыточностью, основным назначением модуляции (модема) является создание наилучшего канала для системы кодирования, в современных СПИ наметилась тенденция к слиянию модема и кодека на основе наиболее эффективного приема сигналов «в целом», т. е. тенденция комплексного решения задачи оптимального преобразования сообщения в сигнал и обратно. В общем случае кодирование и модуляцию необходимо рассматривать как единый процесс формирования наилучшего сигнала, а процесс демодуляции и декодирования — как процесс наилучшего приема сигналов.

Кодеки, и модемы в СПИ выполняют задачу согласования (в информационном отношение) источника сообщений с непрерывным каналом связи. Поэтому при проектировании СПИ их необходимо рассматривать в совокупности как взаимосвязанные подсистемы. Цель состоит в том, чтобы обеспечить наиболее эффективную передачу сообщений от источника к получателю.

Современные СПИ обычно являются многоканальными или системами с многими доступами (многими пользователями). Структурная схема таких систем приведена на рис. 1.7.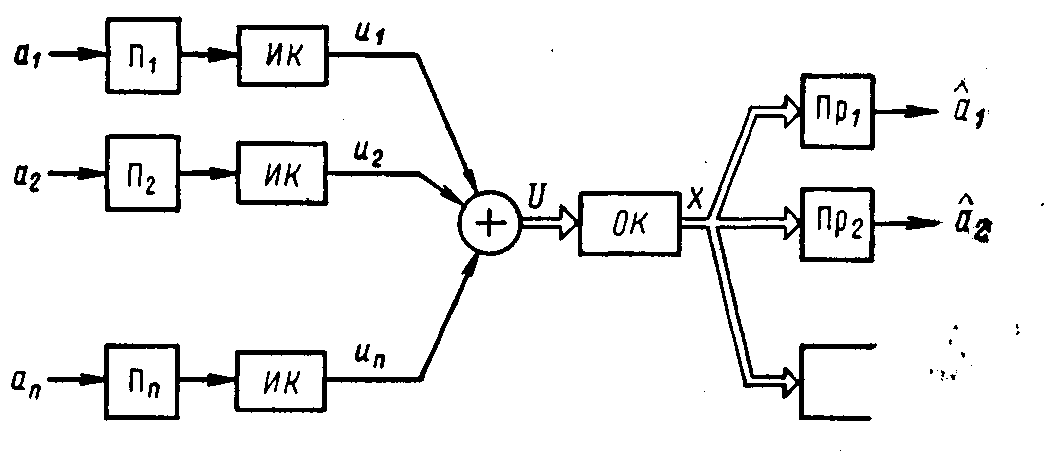


Рис. 1.7 Структурная схема СПИ с многими доступами
Сообщения от п источников а₁ а₂, ..., а_ппреобразуются (в общем случае с помощью кодирования и модуляции) в канальные сигналы u₁(t),u₂(t),…,u_n(t). Эти сигналы сначала передаются по отдельным индивидуальным каналам (ИК), а затем смешиваются, образуя групповой сигнал U(t), который передается по общему каналу (ОК). В состав ОК может входить один или несколько ретрансляторов. На приемной стороне с помощью устройств разделения выделяются сигналы по которым восстанавливаются соответствующие им сообщения.

Канальные сигналы выбирают так, чтобы их можно было разделить на приеме. Необходимым и достаточным условием разделения сигналов, как известно, является условие их линейной независимости. Достаточным является условие их ортогональности. В СПИ широко используют три способа разделения сигналов: по частоте, по времени и по форме. В первом случае каждому сигналу предоставляется отдельная полоса частот и спектры канальных сигналов не перекрываются. Во втором случае сигналы не перекрываются по времени. В третьем случае сигналы отличаются по форме. Они занимают общую полосу частот и передаются одновременно.

Понятия «системы с многими доступами» и «многоканальные системы» аналогичны, хотя и не совпадают. Понятие «многодоступность» является более общим, так как оно охватывает не только процедуру разделения сигналов, но и порядок включения передатчиков. Примерами систем с многими доступами могут служить традиционные многоканальные телефонные и телеграфные системы связи, а также асинхронно-адресные системы. В последнем случае канальные сигналы содержат информацию не только о передаваемом сообщении, но и о номере источника сообщений (адрес источника). Система с многими доступами, которая представлена на рис. 1.7, соответствует случаю, когда источники сообщений значительно удалены друг от друга. Групповой сигнал здесь формируется в два этапа. Сначала в каждом из передатчиков формируются канальные сигналы, а затем происходит их суммирование.

Если источники сообщений расположены близко друг к другу, то сообщения от отдельных источников можно подать на общий передатчик и сразу сформировать групповой сигнал. Такая система имеет много общего с передачей сообщений от одного источника.

1.1.3 Дискретизация непрерывного сигнала

Замена непрерывного сигнала совокупностью выборок (без потери информации) основана на теореме отсчетов (теорема Котельникова): если наивысшая частота в спектре оригинала s(t) меньше чем частота дискретизации F_m, то сигнал s(t) полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга не более чем на 1/2F_m сек.
В соответствии с этой теоремой сигнал s(t), ограниченный по спектру наивысшей частотой 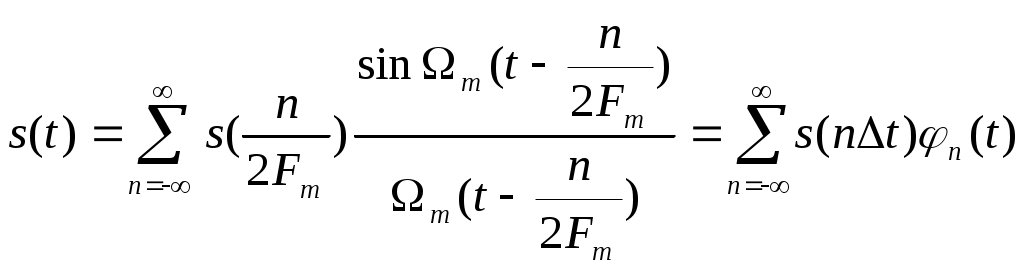, может быть представлен рядом

. (1.3)
В этом выражении l/2F_m =∆tобозначает интервал между двумя отсчетными, a s(n/2F_m) = s(n∆t) — выборки функции s(t) в моменты времени t= n∆t.

Представление заданной функции s(t) рядом (1.3) иллюстрируется рис. 1.8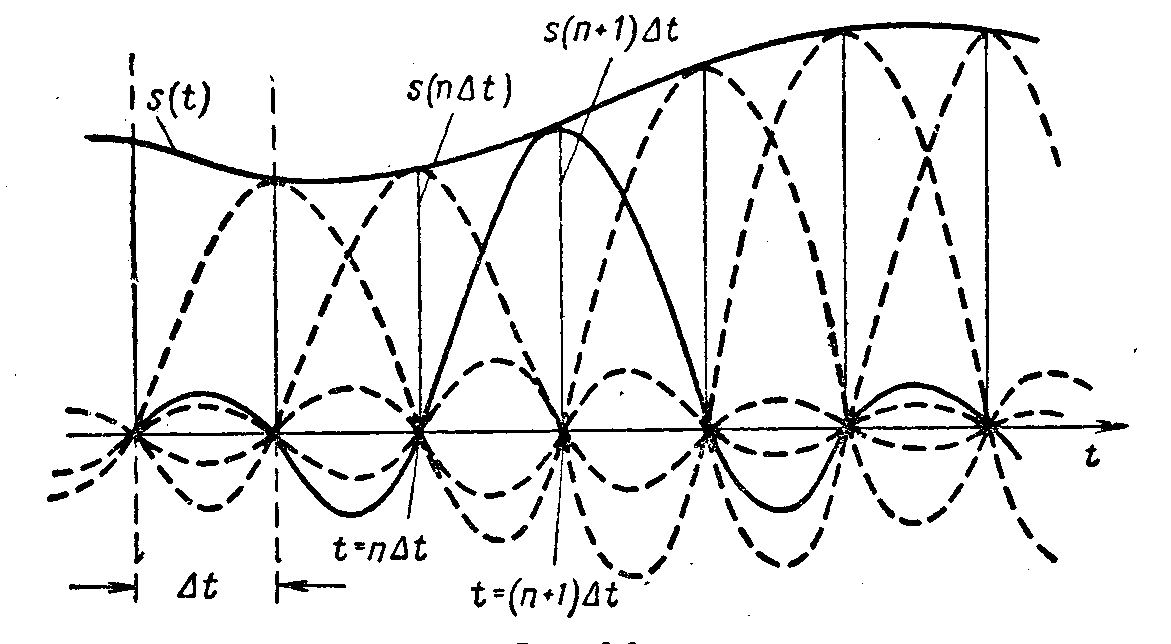

Рис.1.8. Представление сигнала в виде ряда Котельникова
Функция вида
(1.4)

обладает следующими свойствами:

• 
  в точке t= n∆t φ_n(n∆t) = 1, а в точках t=k, где k — любое целое, положительное или отрицательное число, отличное от п, φ_n(k∆t) = 0;
  
• 
  спектральная плотность функции φ₀(t) равномерна в полосе частот 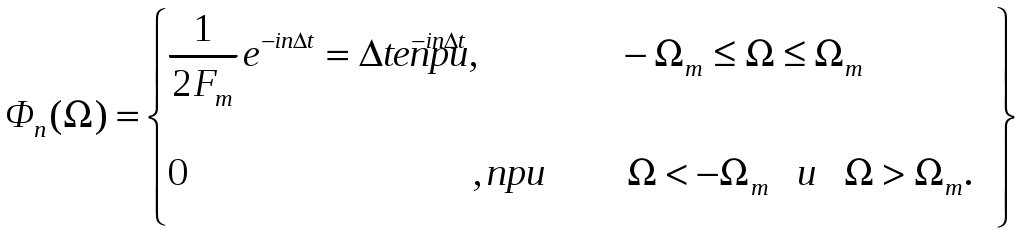и равна 1/2F_m=π/Ω_m. Так как функция φ_n(t) отличается от φ₀(t) только сдвигом на оси времени на величину n∆t, то спектральная плотность функции φ_n(t).
  

. (1.5)
Модуль этой функции изображен на нижней части рис.1.9 (сплошной линией).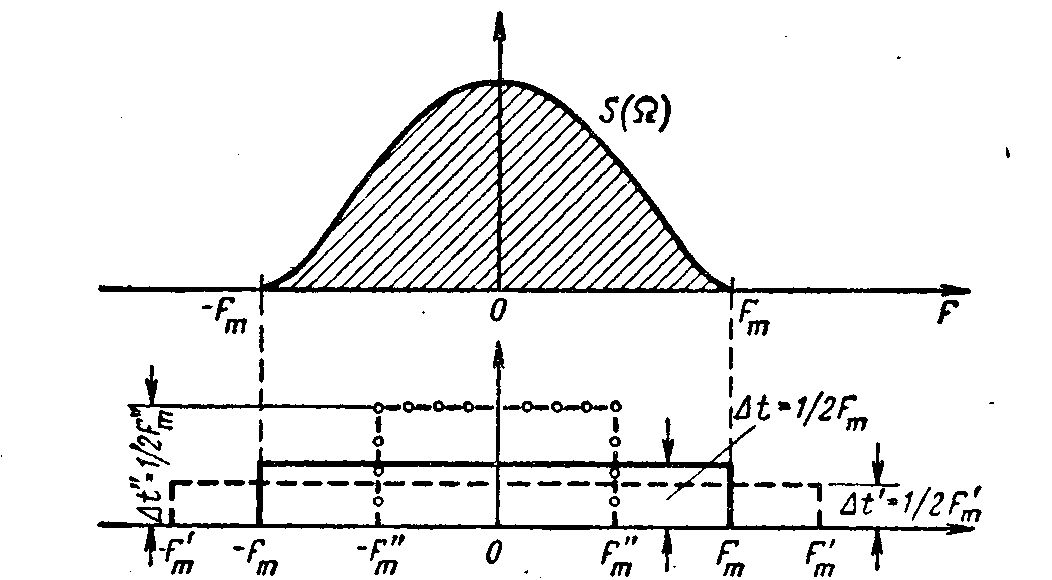


Рис.1.9 Связь между спектром сигнала s(t) и спектром функции
Ряд (1.3) точно определяет заданный сигнал s(t) в точках отсчета, поскольку коэффициентами ряда являются сами выборки из функции, т. е. величины s(n∆t). Можно доказать, что ряд (1.3) определяет функцию s(t) влюбой момент t, а не только в точках отсчета t =n∆t. Воспользуемся для этого общими правилами разложения функции по ортогональной системе. В данном случае разложение производится по функциям вида (1.4), для которых интервал ортогональности равен бесконечности, а норма ||φ_n||: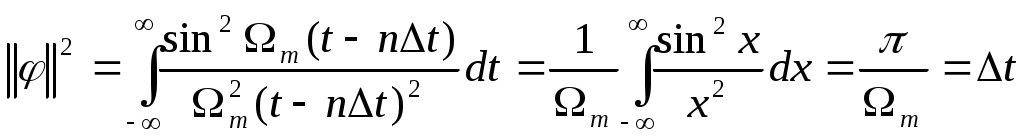
. (1.6)
Применим для определения значений коэффициентов ряда общую формулу, справедливую для обобщенного ряда Фурье:

. (1.7)
Сам обобщенный ряд Фурье представлен коэффициентами:

. (1.8)

При этом исходим из условия, что s(t) — квадратично интегрируемая функция (энергия сигнала конечна).

Для вычисления интеграла в выражении (1.8) воспользуемся формулой , согласно которой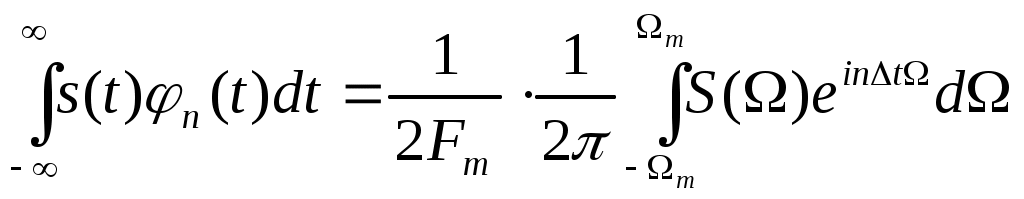
. (1.9)
Пределы интегрирования здесь приведены в соответствие с заданной граничной частотой в спектре сигнала s(0), а также в спектре функции φ_n(t).

Интеграл в правой части (1.9) с коэффициентом 1/2π есть не что иное, как значение s(t) в момент t= n∆t. Таким образом,
. (1.10)

Подставляя этот результат в (1.8), получаем окончательное выражение
(1.11)
из которого следует, что коэффициентами ряда (1.3) являются выборки функции s(t) в точках t = n∆t.

Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции s(t), ряд (1.3) сходится к функции s(t) при любом значении t.

Если взять интервал между выборками ∆t' меньшим, чем ∆t=1/2F_m, то ширина 2F'_m спектра Ф'_n(Ω) функции φ'_n(t) будет больше, чем у спектра S(Ω) сигнала s(t) (рис. 1.8), но это не отразится на величине коэффициентов с_п. Модуль функции Ф'_n(Ω) изображен на рис.1.8 пунктиром.

При увеличении же ∆t'' по сравнению с ∆t спектр Ф''_n(Ω) функции φ''_n(t) (на рис. 1.8 показан штрих-пунктиром) становится уже, чем спектр сигнала s(t), и при вычислении интеграла в выражении (1.9) пределы интегрирования должны быть (-2πF''_m, 2πF''_m) вместо (-2πF_m, 2πF_m). Коэффициенты с_n при этом являются уже выборками не задан­ного сигнала s(t), а некоторой другой функции s₁(t), спектр которой ограничен наивысшей частотой F''_m.

Итак, сокращение интервалов между выборками по сравнению с величиной 1/2F_m допустимо, но бесполезно. Увеличение же интервала сверх величины 1/2F_m недопустимо.

Рассмотрим теперь случай, когда длительность сигнала s(t) конечна и равна Т, а полоса частот по-прежнему равна F_m. Эти условия, строго говоря, несовместимы, так как функция конечной длительности обладает теоретически бесконечно широким спектром. Практически, однако, всегда можно определить наивысшую частоту спектра F_mтак, чтобы «хвосты» функции времени, обусловленные отсеканием ча­стот, превышающих F_m, содержали пренебрежимо малую долю энер­гии по сравнению с энергией заданного сигнала s(t). При таком допущении, если имеется сигнал длительностью Т с полосой частот F_m, общее число независимых параметров т. е. значений s(n∆t), которое необходимо для полного задания сигнала, очевидно, равно

(1.12)

при можно считать N = 2F_mT. При этом выражение (1.3) принимает следующий вид:
(1.13)
Число N иногда называют числом степеней свободы сигнала s(t) так как даже при произвольном выборе значений s(n∆t) сумма вида (1.13) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала. Число N иногда называют также базой сигнала.

В ряде случаев встречается необходимость представления сигнала с помощью частотных выборок спектральной функции S(Ω), а не вре­менных выборок функции s(t). Для функции S(Ω) можно составить ряд, аналогичный выражению (1.3). Это нетрудно сделать на основании взаимной заменимости переменных tи Ω в преобразованиях Фурье. Применительно к выражению (1.3) это означает, что tдолжно быть заменено на Ω, 2Ω_m на Т, 2F_mна Т/2π; ∆t= 1/2F_тна ∆Ω = 2π /Т. Таким образом получается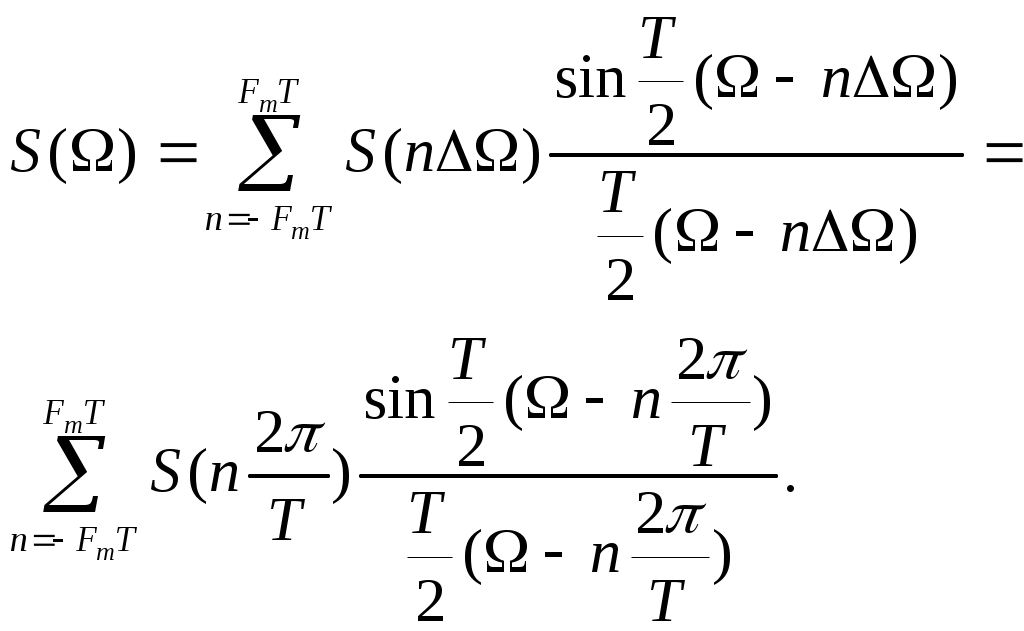

(1.14)
Если ранее временной интервал между двумя соседними выбор­ками должен был не превышать 2π/2Ω_m,то теперь частотный интервал не должен превышать 2π/Т. При ширине спектра 2 Ω_m, охватывающей область частот -Ω_m < Ω < Ω_m, число выборок равно как и при представлении сигнала рядом (1).

В общем случае выборки являются комплексными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра — действительная и мнимая части (или модуль и аргумент). Таким образом, общее число параметров получается вдвое большим, чем при временном представлении сигнала, когда вы­борки — действительные числа. Избыточность представления сигнала в частотной области легко устраняется, если учесть, что и являются комплексно-сопряженными числами, так что задание одной из них однозначно определяет другую. Таким об­разом, число независимых параметров или степеней свободы сигнала равно , как и при представлении сигнала во временной области.

Энергию и среднюю мощность сигнала нетрудно выразить через заданную последовательность временных выборок.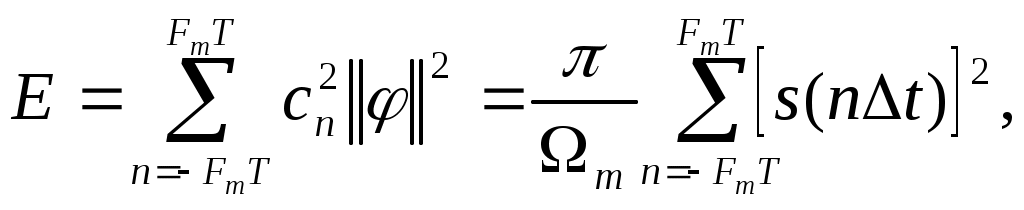
(1.15)

(1.16)
Из последнего выражения видно, что средняя за время Т мощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем отсчетным точкам, число которых равно 2F_mТ.