Учебное пособие по дисциплине. Учебное пособие в оронеж 2006 Воронежский государственный технический университет Е. И. Воробьева

• Название: Учебное пособие в оронеж 2006 Воронежский государственный технический университет Е. И. Воробьева
• Дата: 17.11.2022
• Размер: 5.5 Mb.
• Имя файла: Учебное пособие по дисциплине.doc
• Тип: Учебное пособие; #792926
• страница: 7 из 21

1.4.3 Принципы помехоустойчивого кодирования

Покажем, каким образом избыточное кодирование позволяет повысить верность передачи сообщения. Как отмечалось, для помехоустойчивых блочных равномерных кодов т^п>М. Это значит, что для передачи знаков сообщения используют лишь часть возможных последовательностей, составленных из m-ичных символов (часть пространства n-последовательностей). Последовательности, используемые при кодировании, называются разрешенными кодовыми комбинациями, а все другие n-последовательности — запрещенными. На вход канала поступают только разрешенные комбинации. Если при передаче кодовой комбинации b_i помехи не вызовут ошибок, то на выходе канала возникает та же разрешенная комбинация. Если же один или несколько символов принимается ошибочно, то на выходе канала может возникнуть одна из запрещенных комбинаций.

Таким образом, если комбинация на выходе канала оказывается запрещенной, то это указывает на то, что при передаче возникла ошибка. Отсюда видно, что избыточный код позволяет обнаружить, в каких принятых кодовых комбинациях имеются оши­бочные символы. Безусловно, не все ошибки могут быть обнаружены. Существует вероятность того, что, несмотря на возникшее ошибки, принятая последовательность кодовых символов окажется разрешенной комбинацией (но не той, которая передавалась). Однако при разумном выборе кода вероятность необнаруженной ошибки (т. е. ошибки, которая переводит разрешенную комбина­цию в другую разрешенную комбинацию) может быть сделана очень малой.

Если принята запрещенная кодовая комбинация bj, то, зная параметры канала, можно определить, какая из разрешенных комбинаций b_i вероятнее всего передавалась, и произвести декоди­рование принятой комбинации bj в комбинацию, совпадающую с b_i. Если действительно передавалась b_i, то тем самым возникшее ошибки будут исправлены. Конечно, возможны случаи, когда в действительности передавалась не наиболее вероятная комбина­ция b_i, а какая-то другая, так что декодирование окажется неправильным. Тем не менее, при достаточной избыточности кода и хорошей его структуре вероятность неисправленной ошибки может быть достаточно малой и, во всяком случае, значительно меньшей, чем при примитивном кодировании.

Из сказанного видно, что при избыточном кодировании возможны два основных метода декодирования — с обнаружением ошибок и с их исправлением. Сущность метода декодирования с исправлением ошибок заключается в том, что все множество B принимаемых последовательностей длины n разбивается на M не перекрывающихся подмножеств: В₁,B₂, ..., В_м. Если принята последовательность, принадлежащая подмножеству В_i, то считается, что передавалась кодовая комбинация b_i. Естественно, что в подмножестве В_i следует включить те запрещенные комбинации b_j,при приеме которых наиболее вероятной переданной комбинацией является b_i.

При декодировании с обнаружением ошибок множество B разбивается на М+1 подмножеств, из которых В₁,В₂, ..., В_M содержат каждое по одной (разрешенной) кодовой комбинации, а подмножество В_м+1 — все остальные (запрещенные) комбина­ции. В некоторых системах связи принятая запрещенная комбинация просто отбрасывается и не поступает к получателю. Это обосновано в тех случаях, когда потеря переданного сообщения значительно менее вредна, чем получение ложного сообщения. Чаще при декодировании с обнаружением ошибки ошибочно принятая кодовая комбинация не теряется, а восстанавливается специальными методами. Среди них наиболее распространен метод переспроса.

Необходимо отметить, что правило декодирования с обнаружением ошибок однозначно определяется кодом (т. е. выбором разрешенных комбинаций) и не зависит от свойств канала. При исправлении ошибок, наоборот, возможны различные правила декодирования, поскольку каждую из запрещенных комбинаций можно включить в любое из подмножеств В_i. В зависимости от свойств канала то или иное правило является предпочтительным.

Существуют и смешанные методы декодирования, когда неко­торые ошибки исправляют, а другие только обнаруживают. Здесь множество В также разбито на М+1 подмножеств, но в подмножество В₁ ..., В_м помимо разрешенных комбинаций входят и некоторые близкие к ним запрещенные (исправляемые), а в B_M+1 — только те запрещенные комбинации, которые не могут быть достаточно надежно исправлены.

Говорят, что в канале произошла ошибка кратности q, если в кодовой комбинации qсимволов приняты ошибочно. Легко ви­деть, что кратность ошибки есть не что иное, как расстояние Хэмминга между переданной и принятой кодовыми комбинациями, или, иначе, вес вектора ошибки.

Рассматривая все разрешенные кодовые комбинации и определяя кодовые расстояния между каждой парой, можно найти наименьшее из них d = mind(i;j), где минимум берется по всем парам разрешенных комбинаций. Это минимальное кодовое расстояние является важным параметром кода. Очевидно, что для простого кода d=1.

Обнаруживающая способность кода характеризуется следующей теоремой.

Если код имеет d>l и используется декодирование по методу обнаружения ошибок, то все ошибки кратностью q<.d обнаруживаются. Что же касается ошибок кратностью q≥d, то одни из них обнаруживаются, а другие нет.

Для доказательства достаточно вспомнить, что кодовое расстояние между посланной и принятой комбинациями равно q. Следовательно, если q<d, принятая комбинация не может быть разрешенной, так как это противоречило бы определению d. Поэтому она будет принадлежать подмножеству запрещенных комбинаций, т. е. ошибка будет обнаружена. При q≥dпринятая комбинация может оказаться разрешенной и ошибка останется необнаруженной, но часто и в этом случае принятая комбинация ока­зывается запрещенной и ошибка обнаруживается.

Процесс исправления ошибок рассмотрим сначала для симметричного канала без памяти. В таком канале по определению, вероятность правильного приема символа 1—p не зависит от того, какой символ передается, а также от того, как приняты остальные символы. Вероятность того, что вместо переданного символа b_i- будет принят символ равна р/(т—1). Отсюда легко вывести, что вероятность получения на выходе «канала комбинации , если на вход подана комбинация b_i
(1.41)
Это следует непосредственно из теоремы умножения вероятностей независимых событий и из того, что для перехода b_i в необхо­димо, чтобы на определенных d(i; j) разрядах произошли определенные ошибки, а на остальных разрядах символы были приняты верно.

Таким образом, всимметричном канале без памяти P(bj|bi) зависит только от кодового расстояния между b_i и bj. В случаях, когда р<(т— 1)/т, что практически всегда выполняется, выражение (5.3) монотонно убывает с увеличением d(i; j). Следовательно, вероятность принять комбинацию тем больше, чем меньше ее кодовое расстояние от переданной комбинации b_i.

Задачей декодера является принятие решения о том, какая кодовая комбинация передавалась, если принята комбинация . Разумеется, решение, принимаемое декодером, не всегда верное. Однако можно добиваться минимума вероятности ошибочного декодирования. Пусть Р (b_i | bj) — условная вероятность того, что передавалась комбинация b_i, если принята комбинация . Эту условную вероятность называют апостериорной вероятностью в отличие от безусловной априорной вероятности Р (b_i) того, что передается b_i, когда ничего еще не известно о принятой комбина­ции. Предположим, что декодер по принятой комбинации решил, что передавалась комбинация b_k. Вероятность того, что это решение верно, очевидно, равна P(b_k| ). Чтобы эта вероятность была максимально возможной, декодер должен из всех разрешенных комбинаций b_i(i=1, ..., М) выбрать ту, для которой апостериорная вероятность максимальна. Это правило декодирования по максимуму апостериорной вероятности можно записать сокращенно так:
.
Из теории вероятностей известно, что
, (1.42)
(формула Байеса).

Если, как часто бывает на практике, все разрешенные кодовые комбинации равновероятны то максимум апостериорной вероятности совпадает с максимум условной вероятности , которую называют функцией правдоподобия. Правило декодирования по максимуму правдоподобия можно сокращенно записать так:
, (1.43)
а эта вероятность, как видно, в симметричном канале без памяти определяется только кодовым расстоянием между b_i и b_j. Следо­вательно, в таком канале запрещенную комбинацию b_j следует декодировать, как ту разрешенную комбинацию b_i, которая на­ходится на наименьшем расстоянии от b_j. Иначе говоря, в подмножество В_i - следует включить все те комбинации , которые ближе (в смысле Хэмминга) к , чем в любой другой разрешенной комбинации.

Такое декодирование по наименьшему расстоянию является оптимальным для симметричного канала без памяти. Однако для других каналов это правило может и не быть оптимальным, т. е. не соответствовать максимуму правдоподобия.

Исправляющая способность кода при этом правиле декодирования определяется следующей теоремой.

Если код имеет d>2 и используется декодирование с исправлением ошибок по наименьшему расстоянию, то все ошибки кратностью g<d/2 исправляются. Что же касается ошибок большей кратности, то одни из них исправляются, а другие нет.

Для доказательства покажем, что в условиях теоремы (при q<.d/2) действительно переданная комбинация b_i ближе (в смысле Хэмминга) к принятой комбинации bj, нежели любая другая разрешенная комбинация. Предположим противное, т. е. что существует разрешенная комбинация b_k, для которой d(k; j)<d(i;j). На основании отсюда следует, что d(k;i)≤d(k;j)+d(i;j)<2d(i;j). Но по условию теоремы d(i;j)=q<d/2. Отсюда d(k;i)d. Это противо­речие и свидетельствует о справедливости теоремы.

Полученные результаты можно выразить следующими формулами: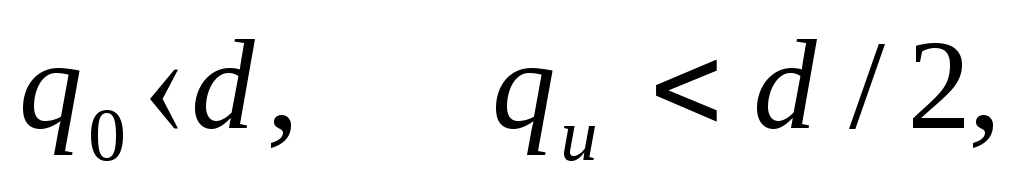

(1.44)

где q₀— кратность гарантированно обнаруживаемых ошибок в режиме, когда ошибки только обнаруживаются; q_и— кратность гарантированно исправляемых ошибок.

1.4.4Линейные двоичные блочные коды

Линейными называются такие двоичные коды, в которых множество всех разрешенных блоков является линейным пространством относительно операции поразрядного сложения по модулю 2. Очевидно, что оно является подпространством линейного пространства, образуемого множеством всех (а не только разрешенных) двоичных последовательностей длины п. Чтобы разрешенные блоки были линейным пространством, они должны содержать нулевой элемент, т. е. блок, состоящий из п нулей, должен быть разрешенным, а сумма (поразрядная по модулю 2) любых разрешенных блоков должна быть также разрешенным блоком. Линейные коды называют также групповыми. Двоичный линейный ,код можно построить следующим образом. Среди всех 2ⁿ последовательностей кодовых символов можно выбрать различными способами п линейно-независимых. В частности, ими могут быть (но не обязательно) элементы, образующие ортогональный базис. Выберем из них kлюбых линейно-независимых блоков, которые обозначим и образуем все линейные комбинации вида
(1.45)
где а_ilпринимает значения 0 или 1, а суммирование — поразрядное по модулю 2. Легко видеть, что множество {bj} этих комбинаций образует линейное пространство, содержащее 2^kблоков, т. е. линейный код.

Действительно, множество {b_i} содержит нулевой элемент, получающийся, когда все а_il = 0 (l=1, ..., k). Сумма любых двух элементов представляет собой также элемент этого множества, поскольку а_il + а_jlпринимает значение 0 или 1. Число элементов множества {b_i} определяется количеством различных наборов из kдвоичных коэффициентов а_ij, которое, очевидно, равно 2^k. Если записать kлинейно-независимых блоков, используемых для построения линейного кода, в виде kстрок, то получится матрица размером , которую называют порождающей или производящей матрицей кода G.

В общем случае производящая матрица двоичного кода записывается в виде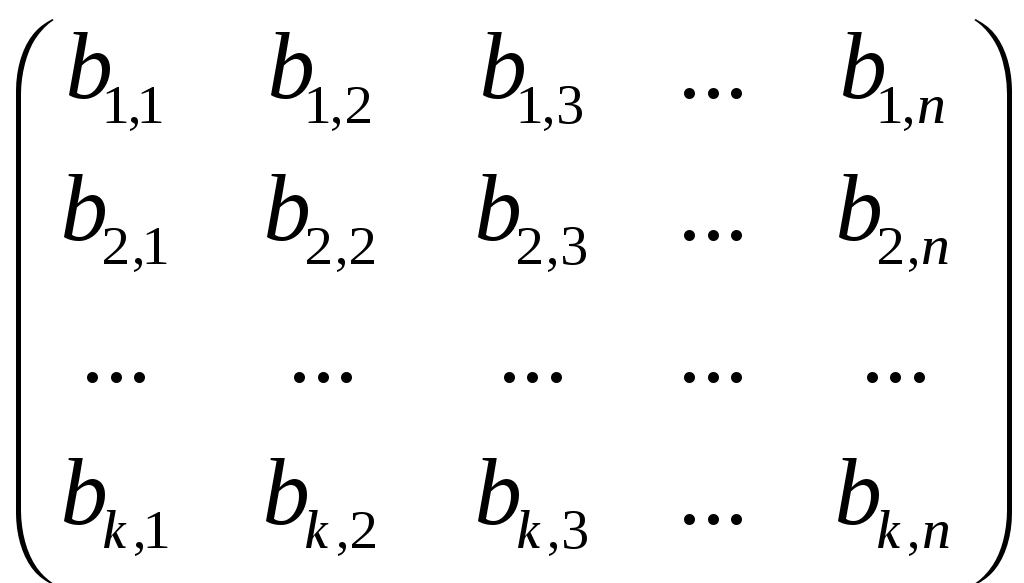
. (1.46)
Здесь b_ij— двоичный символ (0 или 1), находящийся на j-м разряде i-гoкодового слова (входящего в выбранный базис).

Полученный таким образом код, содержащий 2^kблоков длиной я, обозначают (n, k). При заданных п и kсуществует много различных (п, k) -кодов с различными кодовыми расстояниями d, определяемых различными порождающими матрицами. Все они имеют избыточность или относительную скорость V_k = k/n.

Заметим, что если две порождающие матрицы различаются только порядком расположения столбцов, то определяемые ими коды являются изоморфными пространствами. Такие коды называют эквивалентными. Они имеют одинаковые кодовые расстояния между соответственными парами кодовых векторов и, следовательно, одинаковые способности обнаруживать и исправлять ошибки.

Чаще всего применяют систематические линейные коды, которые строят следующим образом. Сначала строится простой код длиной k, т. е. множество всех k-последовательностей двоичных символов, называемых информационными. Затем к каждой из этих последовательностей приписывается r=n—kпроверочных символов, которые получаются в результате некоторых линейных операций над информационными символами. Можно показать, что для каждого линейного кода существует эквивалентный ему систематический код.

Простейший систематический код (п, п—1) строится добавлением к комбинации из п-1 информационных символов одного проверочного, равного сумме всех информационных символов по модулю 2. Легко видеть, что эта сумма равна нулю, если среди информационных символов содержится четное число единиц, и равна единице, если число единиц среди информационных символов нечетное. После добавления проверочного символа образуются кодовые комбинации, содержащие только четное количество единиц, т. е. комбинации с четным весом.

Такой код (n, п-1) имеет d=2, поскольку две различные кодовые комбинации, содержащие по четному числу единиц, не могут различаться в одном разряде. Следовательно, он позволяет обнаружить одиночные ошибки. Легко убедиться, что, применяя этот код в схеме декодирования с обнаружением ошибок, можно обнаруживать все ошибки нечетной кратности. Для этого достаточно подсчитать число единиц в принятой комбинации и проверить, является ли оно четным. Если при передаче комбинации произойдут ошибки в нечетном числе разрядов q, то принятая комбинация будет иметь нечетный вес и, следовательно, окажется запрещенной. Такой код называют кодом с одной проверкой на четность.

Обозначим через b_iсимвол кода (0 или 1), стоящий на i-m месте в кодовой комбинации. Тогда для систематического (п, k)-кода общего вида получаем следующее правило построения комбинаций (b₁, ..., b_k ,b_k+1,, ..., b_n): символы b₁,..., b_kвыбирают в соответствии с передаваемой информацией, а b_i- при i>kопределяют так, чтобы удовлетворялись условия
, (1.47)
где γ_ij коэффициенты (0 или 1), характеризующие данный код. Если набор все коэффициентов γ_ij собрать в таблицу (матрицу), и получим так называемую проверочную матрицу кода H размерности :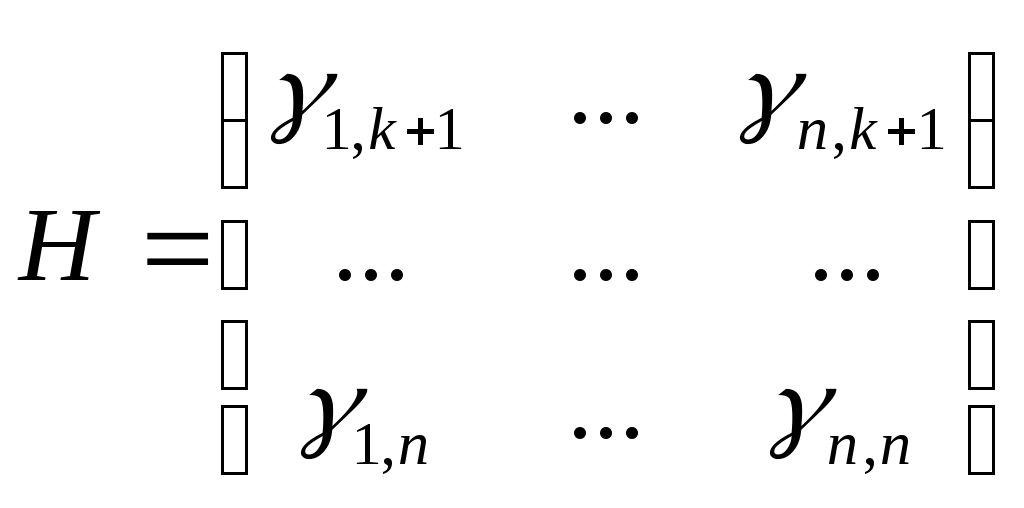
(1.48)
Единицы в каждой j-той строке матрицы H показывают, какие информационные символы нужно сложить по модулю 2, чтобы получить нуль.

Из (1.46) можно придти к выводу, что произведение порождающей и транспонированной проверочной матриц
(1.49)
Для рассмотренного примера кода (п, n—1) с четным весом проверочная матрица вырождается в вектор-строку длиной п:

а порождающая матрица имеет вид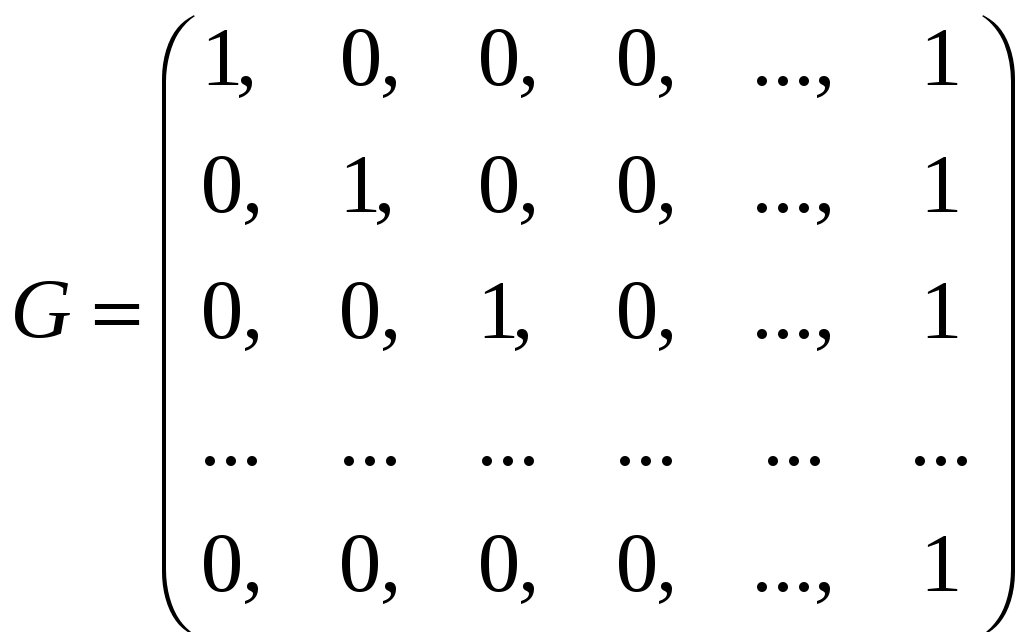

. (1.50)
Рассмотрим другой пример систематического кода — код, заданный порождающей матрицей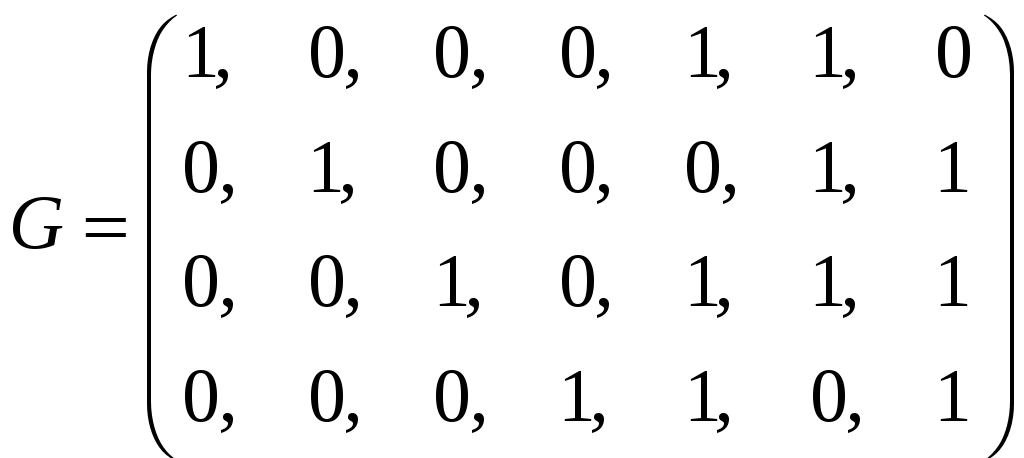
, (1.51)
или проверочной матрицей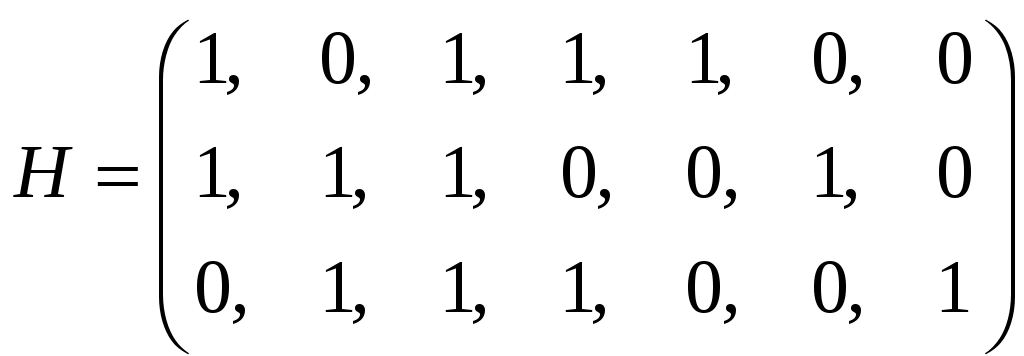
. (1.52)
Этот код имеет d=3 и позволяет обнаруживать все одиночные и двойные ошибки или исправлять (по алгоритму Хэмминга) все одиночные ошибки.

Заметим, что строки проверочной матрицы являются линейно независимыми векторами. Следовательно, проверочная матрица может служить порождающей для другого линейного кода (п, n—k), называемого двойственным. Так, например, матрица (1.51) является порождающей матрицей кода, имеющего d=4. Матрица (1.50) является проверочной для этого кода.

Преимуществом линейных, в частности систематических, кодов является то, что в кодере и декодере не нужно хранить список из 2^kблоков, а при декодировании не нужно вычислять 2^k расстояний. Вместо этого достаточно хранить, например, n—kстрок проверочной матрицы и при декодировании проверять выполнение n—kравенств. Так, например, при коде (100, 50) нужно хранить 50 строк по 100 символов, т. е. всего 5000 символов, а не 10¹⁷, как при табличном кодировании, и проверять 50 равенств, вместо перебора 10¹⁵ расстояний.

Обнаруживать и исправлять ошибки при систематическом коде можно следующим образом. В режиме обнаружения ошибок проверяют выполнение равенств (1.45) и если хотя бы одно из них не выполнено, принятый блок бракуют как ошибочный. В режиме исправления ошибок после проверки равенства (5.19) строится последовательность с= (с₁, с₂, ..., c_n-k), называемая синдромом, где C_j(j=l, ..., п—k) —двоичный символ, равный нулю, если j-е равенство в (1.45) выполнено, и единице, если оно не выполнено. Нулевой синдром указывает на то, что все проверки выполнены, т. е. принятый блок является разрешенным. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется. Так, например, для рассмотренного кода в табл. 1.1 представлены ненулевые синдромы и соответствующие конфигурации ошибок.
Таблица 1.1

Синдром	001	010	011	100
Конфигурация ошибок	0000001	0000010	0100000	0000100
Синдром	101	110	111
Конфигурация ошибок	0001000	1000000	0010000

Таким образом, код позволяет исправить все одиночные ошибки.

Из этого примера видно, что при декодировании систематического кода не требуется перебирать таблицу, содержащую 2^kкодовых комбинаций, и производить п—kсравнений. Помимо тех операций, которые осуществляются в кодере, декодер должен произвести п—kсравнений и перебрать таблицу исправлений, содержащую 2^n-kстрок. Для такого кода, как, это осуществляется просто, но зато код оказывается малоэффективным.

Как неоднократно отмечалось, для получения высокой верности связи следует применять коды с достаточно большой длиной. Однако с ростом п, если отношение k/n(скорость кода) фиксировано, растет и разность п—k, а следовательно, и объем таблицы исправлений, равный 2^n-k. Так, для кода он равен 2¹⁸ = 262 144.

Следовательно, применение систематического кода в общем случае хотя и позволяет упростить декодирование по сравнению с табличным методом, все же при значениях п порядка нескольких десятков не решает задачи практической реализации.

Если (п, k) -код используется для обнаружения ошибок, то в теории кодирования доказывается, что при любой вероятности ошибочного приема символа р≤1/2 найдется код, для которого
(1.53)
Более того, при любых п и kсуществует код, который в любом двоичном симметричном канале без памяти обеспечивает выполнение неравенства (5.25), какова бы ни была вероятность ошибки Такие коды называются равномерно обнаруживающими ошибки.

Таким образом, увеличивая число корректирующих символов, можно обеспечить сколь угодно (малую вероятность необнаруженной ошибки (и, следовательно, вероятность выдачи получателю ложной информации). Однако при сохранении скорости кода k/nэто потребует увеличения длины блока п. При большой длине блока вероятность появления обнаруживаемой ошибки возрастает и, следовательно, увеличиваются трудности восполнения потерянной информации.

К наиболее простым двоичным систематическим кодам относят коды Хэмминга с d=3. Для любого натурального числа rсуществует код Хэмминга при п=2^r—1 и k = n—r. Двойственными кодами к кодам Хэмминга являются эквидистантные коды при n=2^r—1, k = rи d = 2^r-1 ,причем расстояние между любой парой кодовых комбинаций одинаково, чем и обусловлено название кодов. Коды Хэмминга и эквидистантные обладают свойством равномерно обнаруживать ошибки.

Теория помехоустойчивости кодирования достигла больших успехов. Предложен ряд кодов и способов декодирования, при которых сложность декодера растет не экспоненциально, а лишь как (некоторая степень n).

1.4.5 Циклические коды

В поисках более простой техники кодирования и декодирования был найден подкласс линейных систематических двоичных кодов, называемых циклическими и применяемых в технике связи. Название этих кодов связано с тем, что каждый вектор, получаемый из кодового циклической перестановкой его символов, также принадлежит коду. Так, например, циклические перестановки вектора 1000101 являются также кодовыми векторами 0001011, 0010110, 0101100 и т. д.

Теория циклических кодов основана на изоморфизме, пространства двоичных n-последовательностей и пространства полиномов степени не выше п—1 вида


где коэффициенты а принимают значения 0 и 1. Множество таких полиномов образует линейное пространство, если определить сложение полиномов как суммирование коэффициентов при соответствующих степенях х по модулю 2. Переменная х является символической, и ее значение не влияет на свойства пространства.

Легко видеть, что между полиномами и n-последовательностями имеется изоморфизм, причем полиному соответствует n-последовательность

Любой полином g(x) степени rn—1, может служить порождающим полиномом циклического (n, k)-кода, где k=n—r. В этот код входят те полиномы, которые без остатка делятся на g(x). В частности, для кода (7,4) порождающим полиномом является
(1.54)
Среди циклических кодов особое значение имеет класс кодов, предложенных Боузом и Рой-Чоудхури и независимо от них Хоквингемом. Коды Боуза — Чоудхури — Хоквингема (обозначаемые сокращением БЧХ) отличаются специальным выбором порождающего полинома, вследствие чего для них существуют сравнительно просто реализуемые процедуры декодирования. Доказано, что для любой пары натуральных чисел 5 и t<2^s-2 можно построить двоичный код БЧХ с n=2^s—1 и k≥n—st, исправляющий любую конфигурацию ошибок с кратностью, меньшей или равной t.

Относительно простой является процедура мажоритарного декодирования, применимая для некоторого класса двоичных линейных, в том числе циклических кодов. Основана она на том, что в этих кодах каждый информационный символ можно несколькими способами выразить через другие символы кодовой комбинации. Если для некоторого символа эти способы проверки дают неодинаковые результаты (одни дают результат «О», а другие — «1», что может быть только в случае ошибочного приема), то окончательное решение по каждому из информационных символов принимается по мажоритарному принципу, т. е. по большинству. Мажоритарное декодирование осуществляется относительно просто, посредством регистров сдвига.

Примером кода, допускающего мажоритарное декодирование, является код, двойственный рассмотренному ранее коду Для него матрица (1.52) является образующей. Ее удобнее записать, переставив столбцы, так: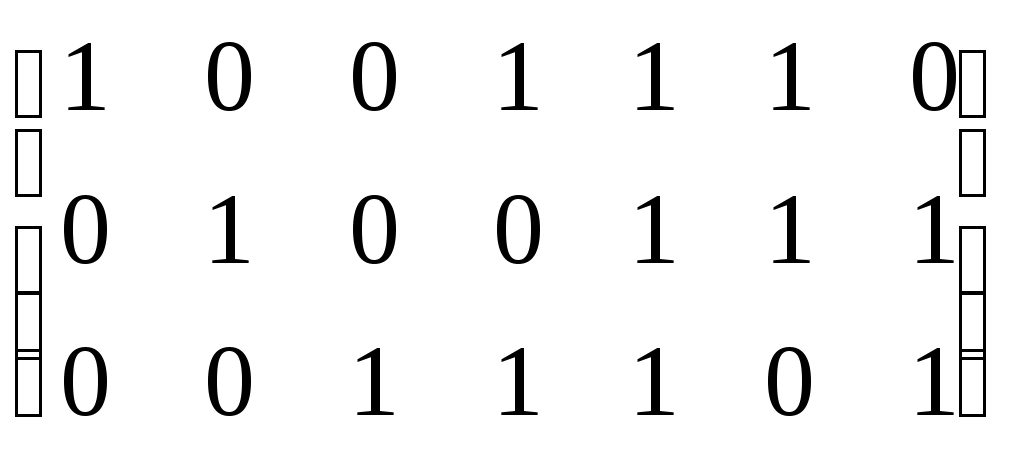
(1.55)
Символ b₁в этом коде связан с другими символами следующими соотношениями: b₁=b₂+b₆=b₇+b₅=b₃+b_4. Обозначим принятые после демодуляции , , , , , , .Если бы они все были приняты верно, то для переданного символа были бы верны следующие четыре равенства (проверки):
(1.56)
Каждый из символов принятого блока входит только в одну из этих проверок для b₁. Код, для которого выполняется это условие, называется кодом с разделенными проверками.

Предположим, что один из символов блока принят с ошибкой. Тогда три из проверок (1.56) дадут одно (правильное) значение b₁,а одна проверка, в которой участвует ошибочный символ, даст другое, ошибочное значение. Принимая решение по большинству получим правильное значение b₁. Если бы ошибок было три или больше, то мажоритарное решение могло бы дать ошибочный результат. При двух ошибочно принятых символах может получиться одинаковое (верное) значение для b₁во всех проверках (например, при ошибочно принятых и ) либо в двух проверках b₁ = 0, а в двух других b₁=1 (например, при ошибочно принятых и ). В последнем случае можно только констатировать наличие ошибок.

После принятия решения о символе b₁аналогично проверяют значения b₂и b₃. Поскольку рассматриваемый код (7, 3)—циклический, соответствующие проверки получаются из (1.56) циклической перестановкой.

1.4.6 Сверточные коды

Кодирующее устройство двоичного сверточного кода (рис. 1.16) представляет собой регистр сдвига, состоящий из kячеек, к выходам которых в определенном порядке подключены п сумматоров по модулю 2. Двоичные информационные символы, поступающие в регистр от источника информации, сдвигаются в регистре на q<kсимволов, после чего выходы сумматоров по модулю 2 опрашиваются коммутатором и полученная последовательность двоичных символов с выхода коммутатора направляется на модулятор передатчика. Далее этот процесс повторяется. Полученный таким образом код называется сверточным, или рекуррентным кодом. Параметры k, n и qипорядок подключения сумматоров по модулю 2 к ячейкам регистра сдвига определяют структуру получаемого сверточного кода. Избыточность такого кода Rи=1--q/n. Эквивалентная длина сверточного кода равна k.

На рис. 1.17 изображено кодирующее устройство сверточного кода. В исходном состоянии в регистре записаны нули. Приходящий от источника первый информационный символ записывается в первую ячейку регистра, и коммутатор опрашивает сумматоры по модулю 2, в результате чего формируются два символа сверточного кода. При приходе второго информационного символа первый символ переписывается во вторую ячейку регистра, а второй информационный символ записывается в первую ячейку. Коммутатор вновь опрашивает сумматоры по модулю 2 и т.д. По окончании всей кодируемой последовательности информационных символов в регистр подаются три нуля и регистр приводится в исходное состояние.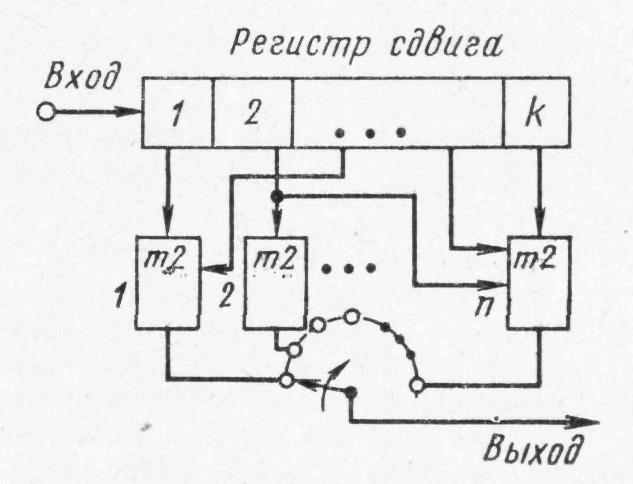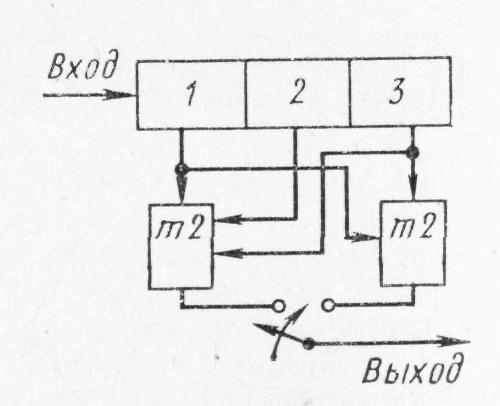



Рис. 1.16. Кодирующее устройство двоичного сверточного кода.

Рис. 1.17 Кодирующее устройство двоичного сверточного кода при k = 3, n = 2, q=l.



Работу кодирующего устройства сверточного кода удобно пояснить с помощью кодового дерева (рис. 1.18). Кодовое дерево строится следующим образом. Если входной информационный символ, поступающий в сдвигающий регистр, равен 1, то ему приписывается линия (ветвь дерева), идущая, например, вниз, а если информационный символ равен 0- -то вверх. Символы сверточного кода, получаемые на выходе сумматоров по модулю 2, записываются над соответствующей ветвью дерева. Точки, из которых исходят ветви дерева, называются узлами. Определенная последовательность информационных символов на входе кодирующего устройства порождает один из путей по кодовому дереву.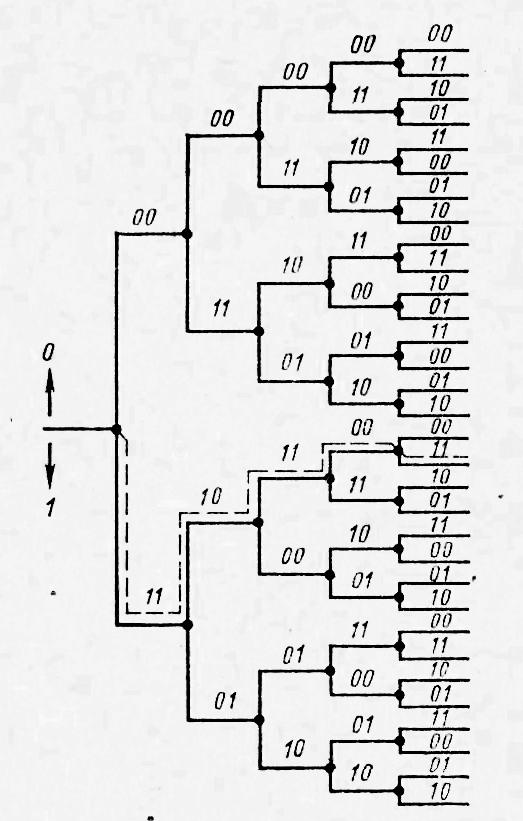



Рис. 1.18. Кодовое дерево, соответствующее кодирующему устройству рис. 1.17.
Например, входная последовательность информационных символов 10001..., поступающая на кодирующее устройство (рис. 1.15), порождает выходную последовательность 1110110011 .... Соответствующий путь по кодовому дереву показан на рис. 1.18 пунктирной линией.

Таким образом, процесс кодирования для сверточного кода можно представить как последовательный выбор одного из путей по кодовому дереву. Выбор этого пути задается входной последовательностью информационных символов. В рассмотренных кодирующих устройствах сверточного кода выходные символы вычисляются посредством линейных операций (суммирование по модулю 2) над входными. Поэтому полученные сверточные коды являются линейными.

Если для каждой ветви кодового дерева в выходной последовательности символов присутствуют без изменений входные символы, породившие эту ветвь, то сверточный код называется систематическим. В противном случае код называется несистематическим.

Для декодирования сверточных кодов разработан ряд эффективных методов декодирования, в частности, последовательное декодирование и декодирование А. Витерби .

Принцип последовательного декодирования в двоичном дискретном канале состоит в следующем, п регенерированных символов сверточного кода, соответствующих одной из ветвей кодового дерева, на приемной стороне записывается в регистр сдвига. Декодирующее устройство, аналогичное кодирующему устройству данного сверточного кода, генерирует п символов сверточного кода, соответствующих каждой из ветвей кодового дерева, исходящей из данного узла. Каждая из двух последовательностей п символов, генерируемых в декодирующем устройстве, поразрядно суммируется по модулю 2 с принятой последовательностью, записанной в регистре. В результате этих операций вычисляется расстояние Хэммннга d_Х между этими последовательностями и принятой последовательностью. Затем выбирается путь с наименьшим d_Хи выносится предварительное решение, что путь по данной ветви кодового дерева и является истинным. Расстояние d_Х для этого пути запоминается, и декодирующее устройство переходит к следующему узлу кодового дерева, к которому при водит выбранный путь. Из этого нового узла вновь исследуются два возможных пути п т. д.

Если вероятность искажения одного символа шумами при передаче равна p, то математическое ожидание числа ошибок, а следовательно, и расстояние Хэмминга d_Х. между принятыми п символами сверточного кода и п символами, соответствующими правильному пути по данной ветви кодового дерева, будет равно пр.

Если же по данной ветви выбран неправильный путь, то математическое ожидание расстояния d_Xдля него будет приблизительно равно n/2. Следовательно, через l последовательных шагов декодирования математическое ожидание d_x(l) для правильного пути будет равно lпр, а для неправильного пути ln/2. Действительные значения d_x(l) для правильного п неправильного пути будут случайными величинами с указанными математическими ожиданиями. Это показано на рис. 1.19.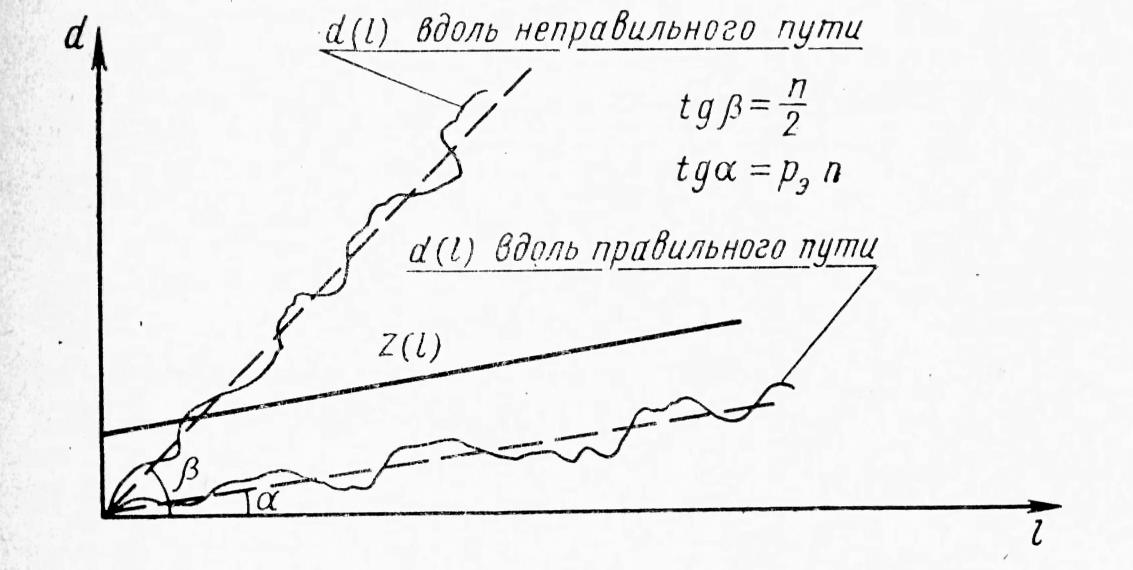


Рис. 1.19. Зависимость кодового расстояния для правильного и неправильного путей.
В последовательном декодирующем устройстве сравнивается текущее значение d_x(l) с некоторым порогом z(l) (рис. 1.19). Если на текущем шаге декодирования порог не превышен, то декодирующее устройство переходит к анализу путей, ведущих из следующего узла. Если порог превышен, то декодирующее устройство возвращается в прошлый узел, для которого не было превышения порога, и исследует другие возможные пути по. кодовому дереву. Таким образом, декодирующее устройство обследует все доступные узлы до тех пор, пока не найдется пути, при котором текущий порог z(t) не превышается. Если же такого пути не находится, то порог повышается и указанная операция повторяется.

Поскольку связи между символами на выходе сверточного кодирующего устройства, имеющего k-разрядный регистр сдвига, распространяются на kветвей кодового дерева, то, найдя один из путей по kветвям дерева, удовлетворяющий установленному порогу, декодирующее устройство выносит окончательное решение о декодировании первой ветви, соответствующей этому пути. Далее так же декодируется вторая ветвь дерева, и т. д. В таком процессе ошибка при декодировании произойдет, если неправильный путь по кодовому дереву не будет обнаружен на протяжении kпоследовательных ветвей.

Достоинством последовательного декодирования является то, что при исключении какого-либо пути по кодовому дереву отбрасываются все другие пути, исходящие из узлов исключенного. За счет этого экономится число операций, производимых при декодировании. Чем выше порог z(l), тем большее количество операций требуется, так как неправильный путь, начавшийся из некоторого узла, обнаруживается позднее. Поэтому сначала декодирование ведут при низком (жестком) пороге; при этом пороге декодируется большинство символов сверточного кода. Если же путей, удовлетворяющих этому порогу, не находится (а это случается значительно реже) порог повышают.

Хотя среднее число операций на один декодированный символ, производимых. при последовательном декодировании, невелико, фактическое число операций величина случайная, меняющаяся в широких пределах. Эта неравномерность вычислительной нагрузки является недостатком последовательного декодирования. Кроме того, в случаях, когда происходит длительный поиск правильного пути по кодовому дереву, возможно переполнение регистра, в котором записываются принимаемые символы сверточного кода.

Рассмотрим теперь принципы декодирования сверточных кодов по методу Витерби. Для этого вновь рассмотрим кодирующее устройство сверточного кода, изображенное на рис, 1.17. В рассматриваемом случае выходные символы сверточного кода, появляющиеся после каждого цикла опроса коммутатором сумматоров по модулю 2, определяются тремя последовательно поступившими информационными символами, записанными в регистре перед опросом коммутатора, или, что то же, состоянием 2-х первых ячеек регистра и последним ступившим символом. Учитывая это, изобразим кодовое дерево, соответствующее этому кодирующему устройству, в несколько другом по сравнению с рис. 1.18 виде.

На рис. 1.20 четыре возможных состояния первых двух ячеек регистра сдвига кодирующего устройства обозначены цифрами 00, 01, 10, 11, заключенными в рамку. По приходе на кодирующее устройство очередного информационного символа первые две ячейки регистра меняют свои состояния. Если приходящий информационный символ «1», то возможный переход состояния показан пунктирной линией, если «0» — то сплошной линией. Цифрами 1, 2, 3 ... обозначены тактовые моменты прихода на кодирующее устройство информационных символов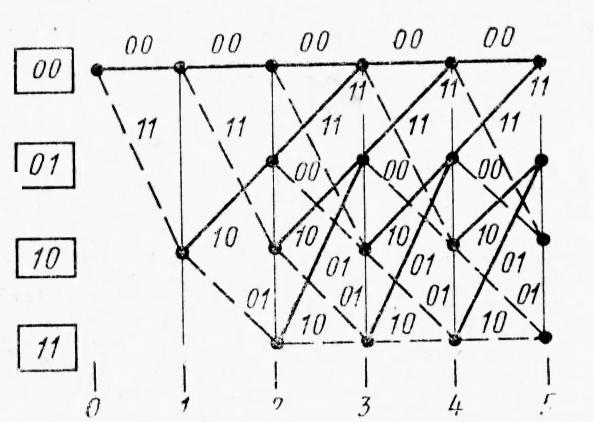


Рис. 1.20. Другой вид кодового дерева сверточного кода.
В исходном состоянии, соответствующем такту с номером 0, в регистре записаны нули. Выходные символы сверточного кода, порождаемые приходящим информационным символов, показаны около соответствующих переходов.

Из рис. 1.20 следует, что, начиная с третьего такта, структура кодового дерева повторяется, и каждое из 4 возможных состояний регистра определяется только двумя предшествующими состояниями. Например, состояние 01 на третьем такте имеет два входных пути по кодовому дереву, соответствующих информационным символам 110 и 010. Эти пути разошлись в такте 0 и слились в такте 3. В общем случае, если регистр кодирующего устройства содержит kячеек и информационные символы перед каждым опросом коммутатора сдвигаются на qячеек, то структура кодового дерева повторяется через kтактов, а пути сливаются через q(k-1) последовательно поступающих одинаковых информационных символов.

Для двоичного симметричного канала без памяти задачей оптимального декодирующего устройства, работающего по максимуму правдоподобия, является выбор такого пути по кодовому дереву, который имеет минимальное расстояние Хэмминга от принимаемой последовательности символов сверточного кода. Поскольку ветви дерева сливаются, то для декодирования по максимуму правдоподобия нет необходимости рассматривать всю полученную последовательность символов сверточного кода. Сразу после k-гoтакта (на рис. 1.20 после 3-го такта) можно решить, какой один из 2^qпутей, ведущих в данное состояние, наиболее правдоподобен, а остальные пути исключить из дальнейшего рассмотрения. Это делается для каждого из 2^q(k-1) состояний в данном такте. Затем декодирующее устройство переходит к следующему такту и процесс повторяется.

Рассмотрим, например, состояние 01 на третьем тракте (рис. 1.20). К этому состоянию ведут два пути по кодовому дереву: первый путь 110101, соответствующий информационным символам 110, и второй путь 001110, соответствующий информационным символам 010. Пусть, например, получена последовательность символов сверточного кода 000110. Эта последовательность имеет расстояние Хэмминга d_x=4 от первого пути и d_x=1 от второго пути, и следовательно, первый путь можно исключить из дальнейшего рассмотрения.

Если окажется, что оба пути, ведущие в данное состояние, имеют одинаковое расстояние Хэмминга от принятой последовательности, т. е. они сливаются, то выбирается любой случайным образом и дальнейшие принимаемые символы никакой дополнительной информации об этих путях не дадут.

Описанное декодирование называется декодированием по методу Витерби. Таким образом, при декодировании по методу Витерби декодирующее устройство хранит в памяти множество из 2^q(k-1) наиболее вероятных путей на каждом шаге декодирования. Окончательный выбор одного, наиболее вероятного пути, может осуществляться посредством передачи в конце сообщения, состоящего из N информационных символов, k-qзаранее известных символов (например нулей, которые приводят декодирующее устройство в исходное состояние).

Как последовательное декодирование, так и декодирование но методу Витерби перспективно для использования в каналах с независимыми ошибками. Количество операций, необходимое для декодирования по методу Витерби N информационных символов, равно N/2^q(k-1) Сложность декодирующего устройства, оцениваемая числом необходимых при декодировании операций, линейно зависит от N, что является достоинством этого метода. Однако количество операций экспоненциально зависит от k, поэтому этот метод используется лишь для относительно небольших k. Для всех сверточных кодов увеличение k, подобно увеличению длины кодового слова при блочном кодировании, при прочих равных условиях ведет к экспоненциальному уменьшению вероятности ошибки при декодировании. Поскольку сложность, последовательного декодирования мало зависит от k, его целесообразно применять при малых вероятностях ошибки на декодированный символ (р≤10^-3-10^-5[105]). При больших вероятностях ошибки целесообразно декодирование по методу Витерби.

Особенностью сверточных кодов является то, что при их декодировании не нужна синхронизация перед началом передачи информации, тогда как для блочных кодов без синхронизации по словам правильное декодирование в большинстве случаев невозможно. Действительно, декодирующее устройство, несинхронизированное перед началом передачи, эквивалентно синхронизированному, но сделавшему одну или несколько ошибок. Моделирование показало, то через (3-5)k синхронизация устанавливается автоматически. Однако для этого требуется надежная синхронизация узлов кодового дерева, т. е. синхронизация по группам символов, соответствующих одному циклу опроса коммутатора сумматоров по модулю 2 в кодирующем устройстве сверточного кода.